Красивый способ рисования параболы придумал итальянский математик Бонавентура Кавальери (итал. Bonaventura Francesco Cavalieri, лат. Cavalerius, 1598—1657) ещё в XVII веке.
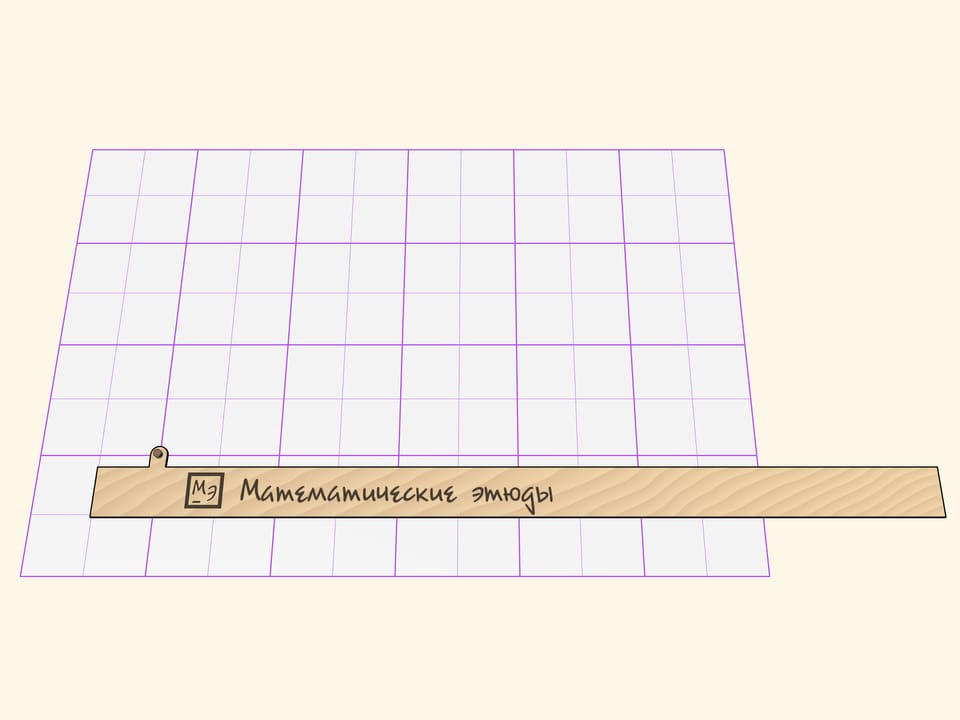
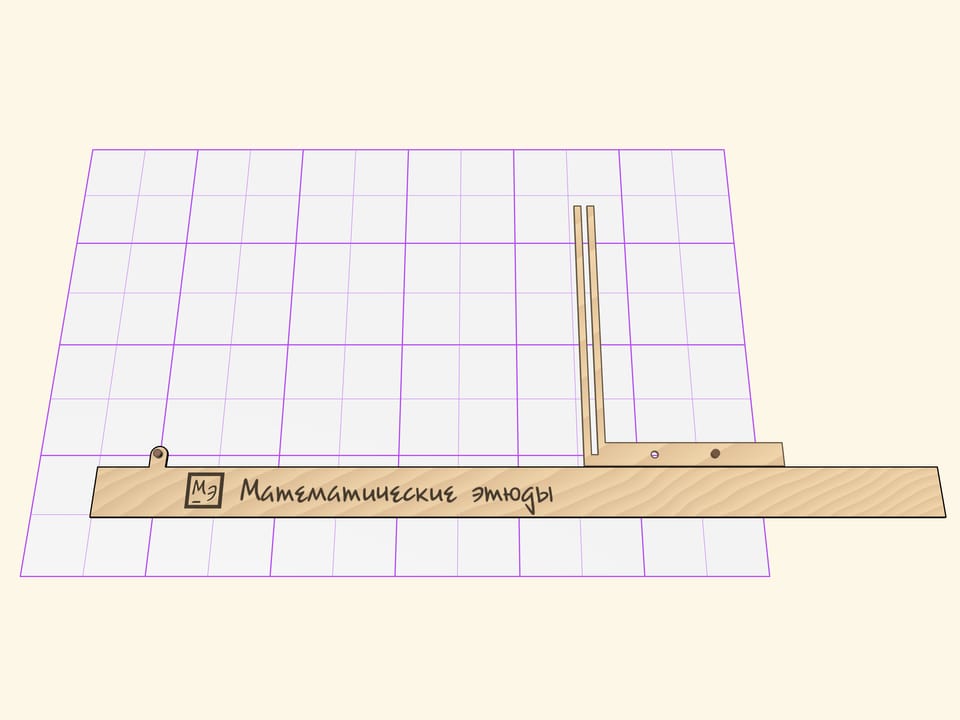
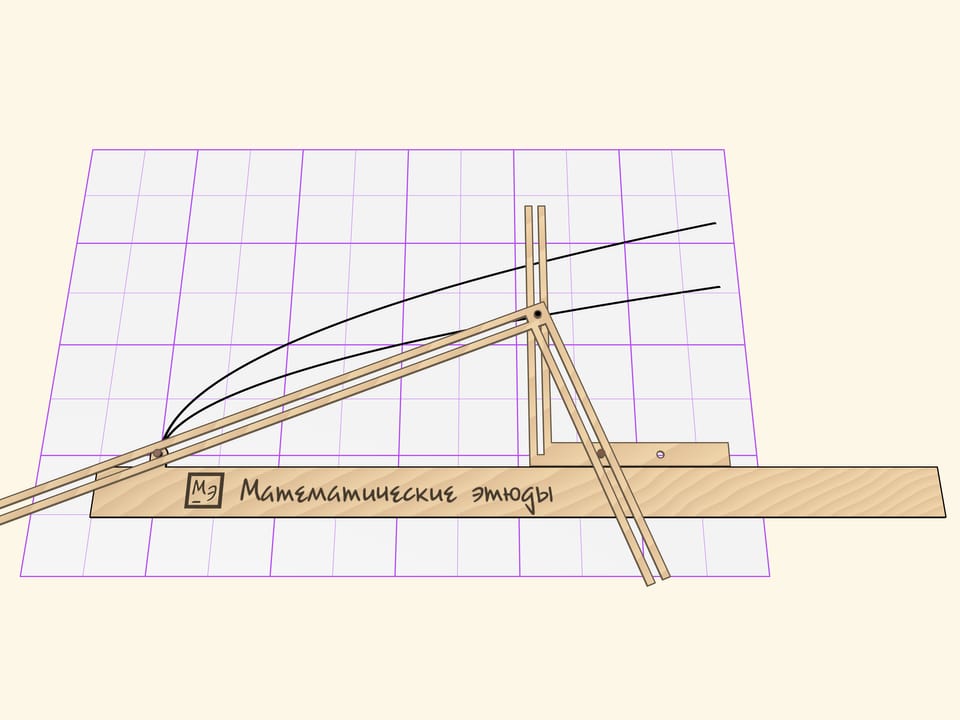
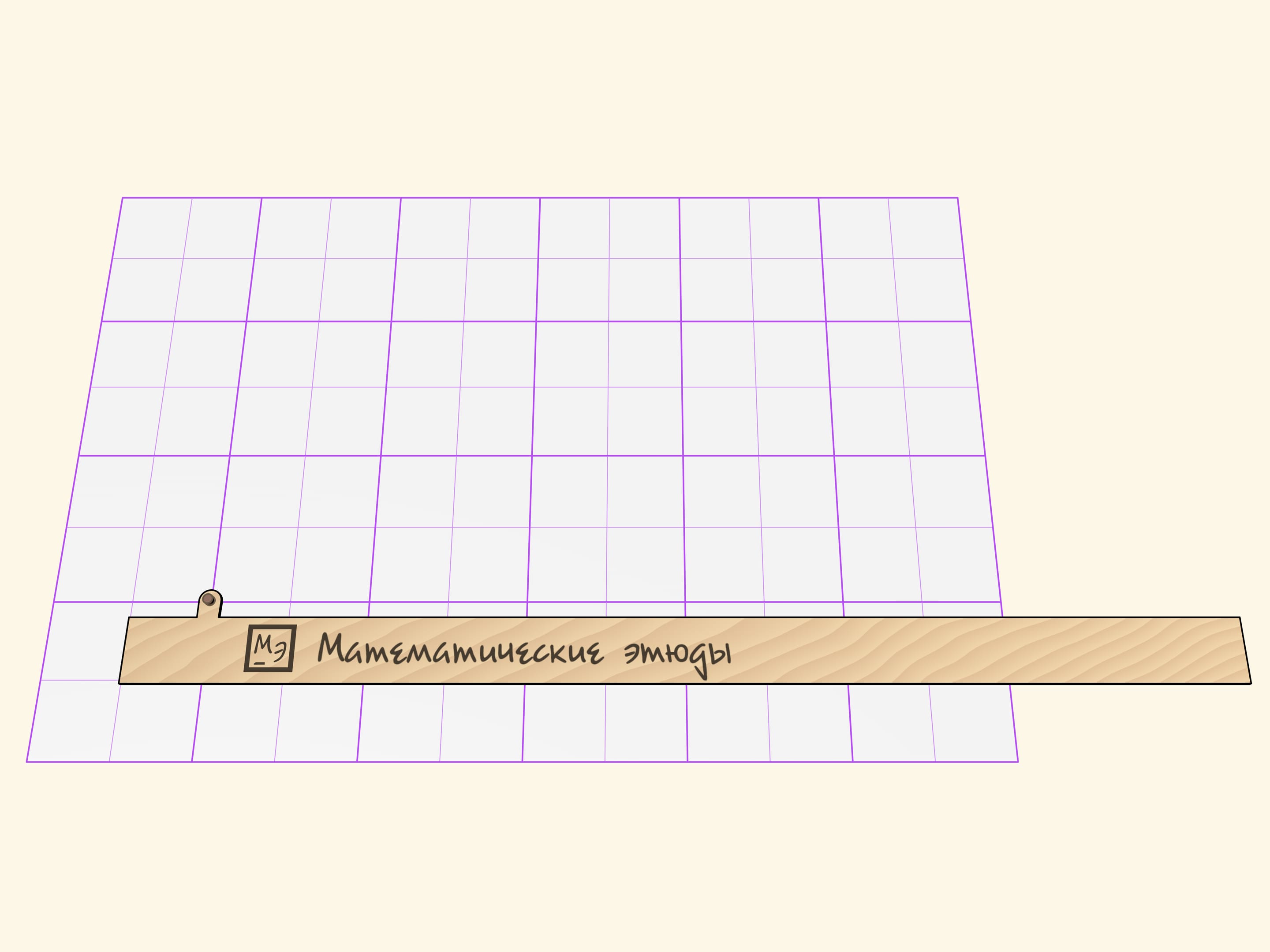
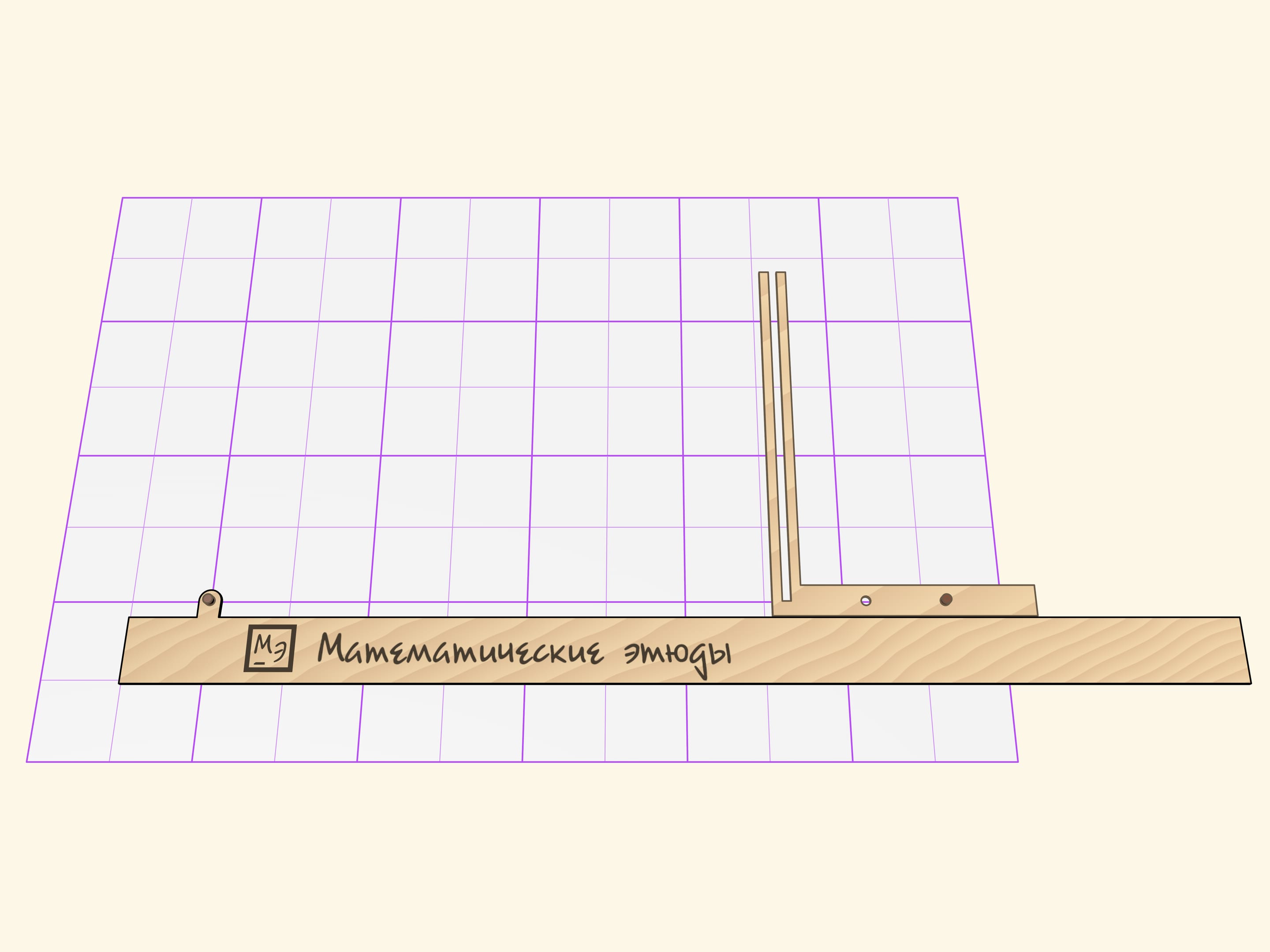
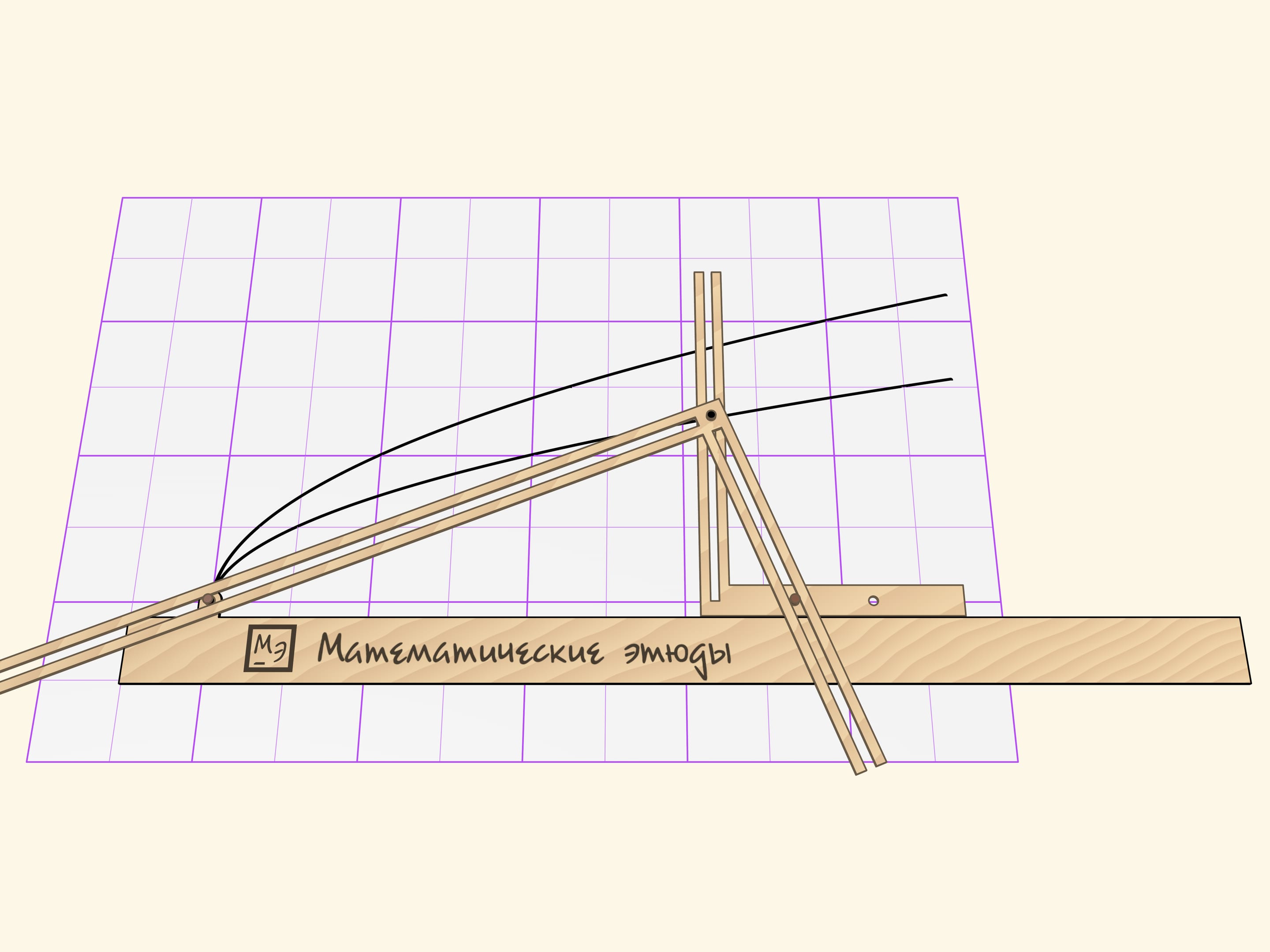
Параболограф Кавальери состоит из трёх частей: линейки и двух жёстких прямых углов, стороны которых имеют прорези.
По неподвижной относительно листа линейке один прямой угол скользит так, что его горизонтальная сторона постоянно соприкасается с линейкой.
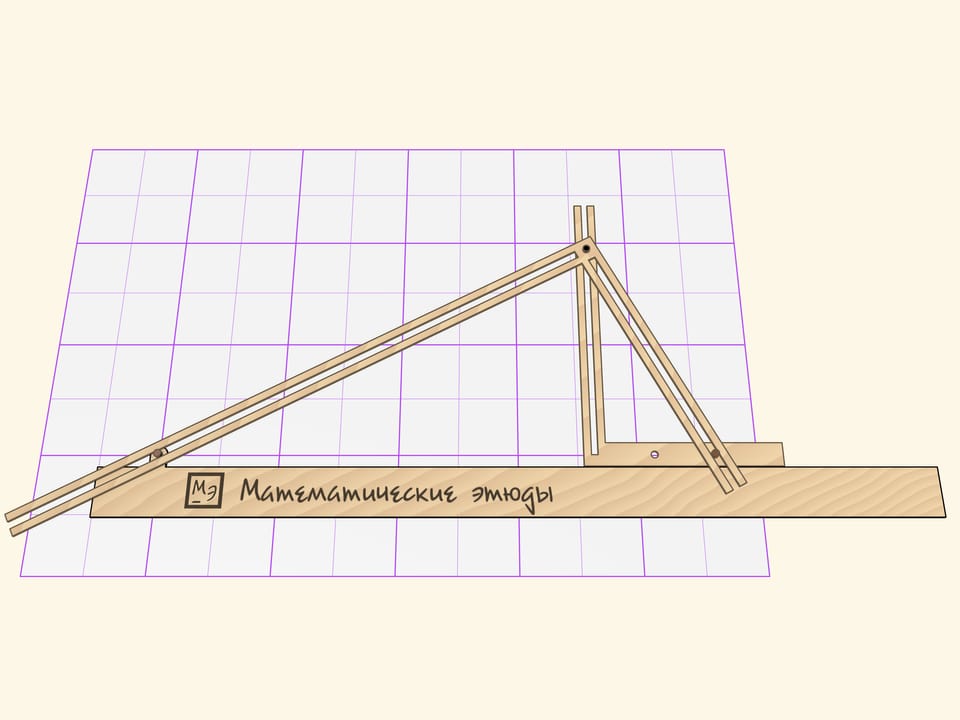
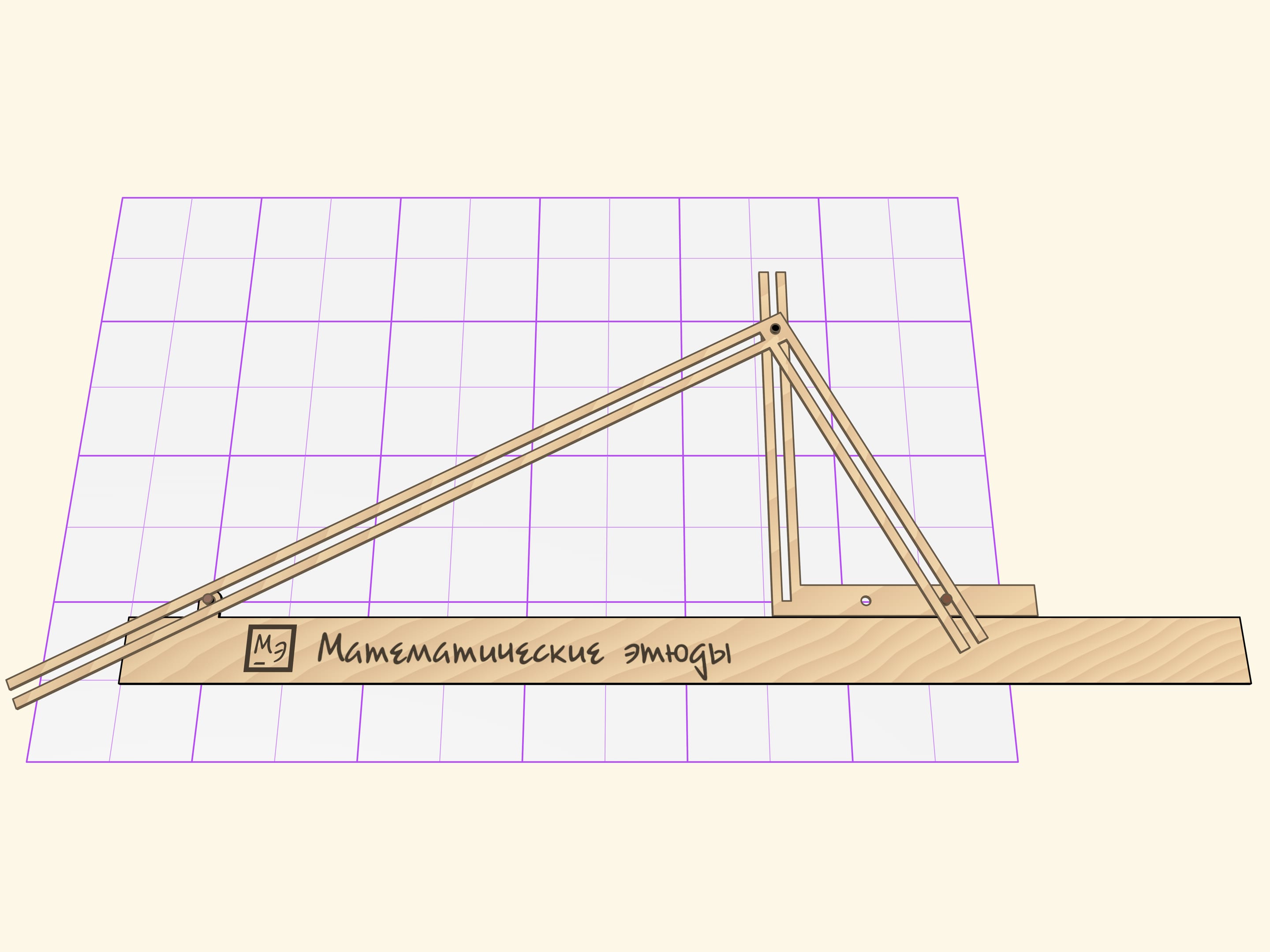
Второй прямой угол образует с линейкой прямоугольный треугольник. Вершина при прямом угле снабжена грифелем и скользит по направляющей прорези вертикальной стороны первого прямого угла. Две другие стороны второго прямого угла скользят своими прорезями по направляющим штифтам, один из которых жёстко закреплён на линейке, а другой — на горизонтальной стороне подвижного угла.
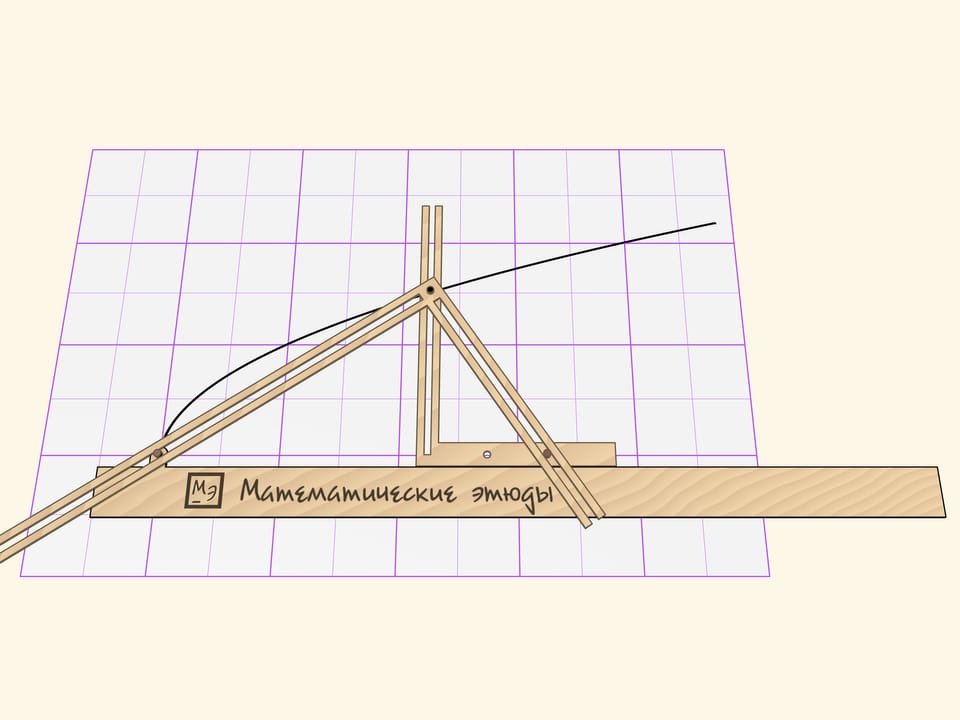
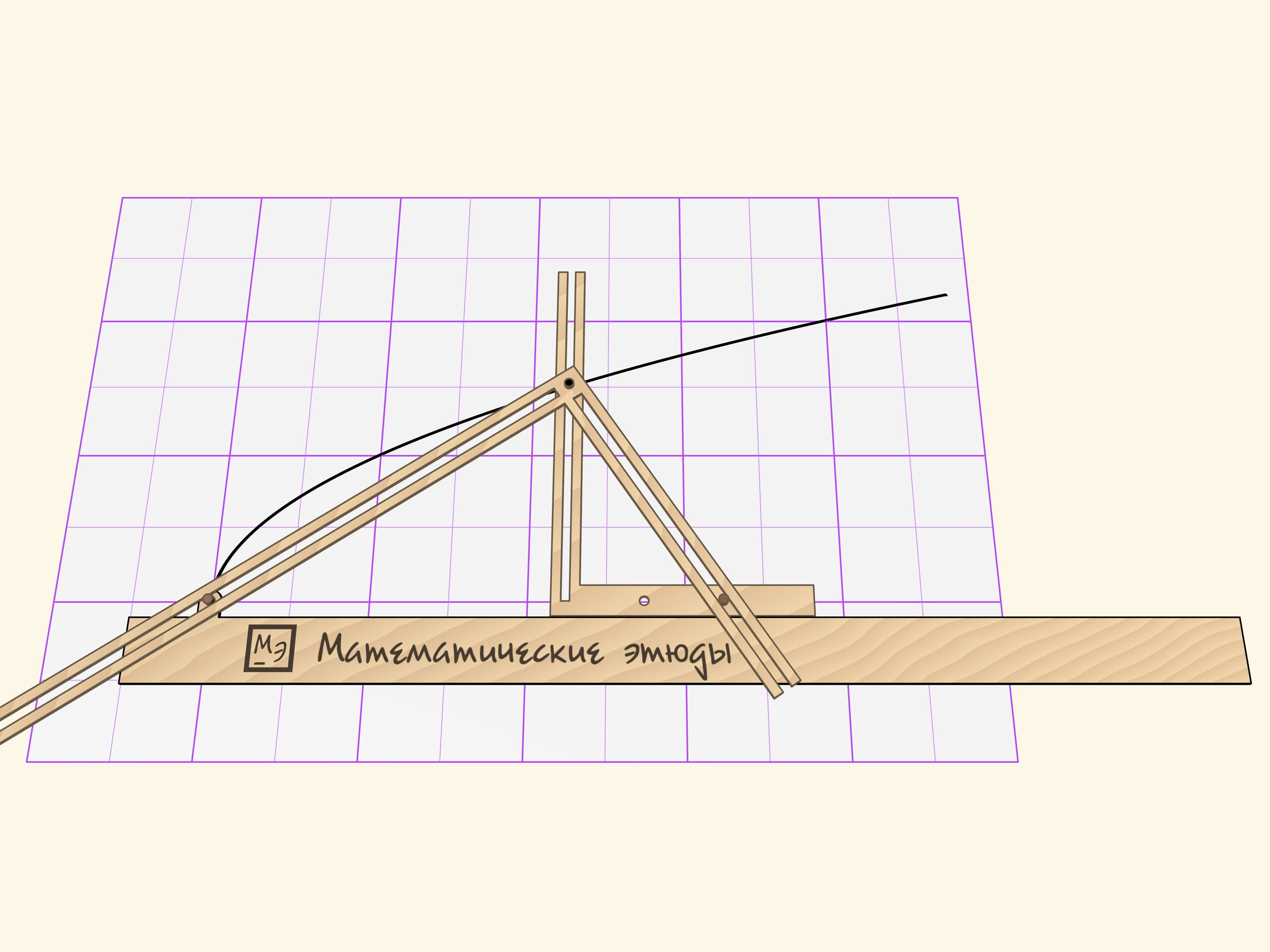
При движении параболографа Кавальери грифель рисует параболу. Параметром параболы является расстояние от штифта до вершины прямого угла, прилегающего к линейке. Если штифт переставить, кривая будет другой, но тоже параболой.
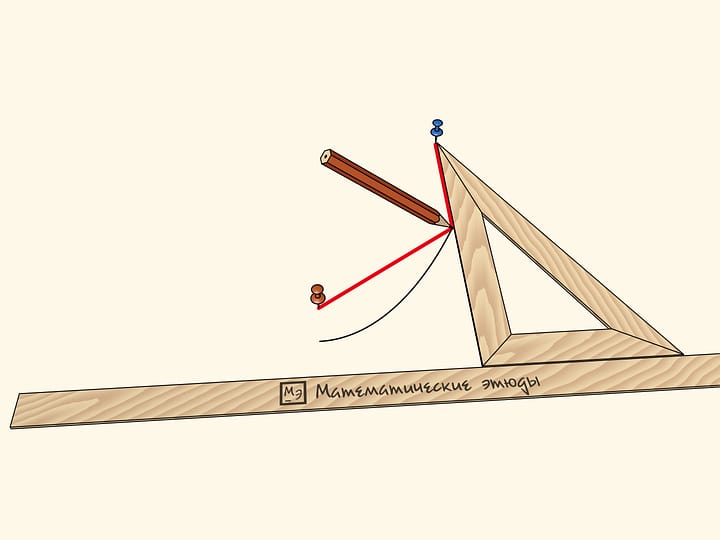
Доказательство того, что рисуемая кривая — парабола, основано на теореме из современного школьного курса математики. Следует рассмотреть треугольник, образованный сторонами второго прямого угла и линейкой. В нём квадрат длины высоты (расстояние от грифеля до линейки), опущенной на гипотенузу-линейку, равен произведению проекций катетов на гипотенузу. Проекция «правого» катета по конструкции параболографа фиксирована и является параметром, определяющим параболу.
Литература
Параболическая антенна // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 46—47, 297—302.