Софокусные эллипсы Грейвза⁠

Постро­е­ние ⁠⁠эллипса с помощью нити откры­вает дорогу к постро­е­нию софо­кус­ных эллип­сов и «дарит» любопыт­ные факты из жизни этих кри­вых.

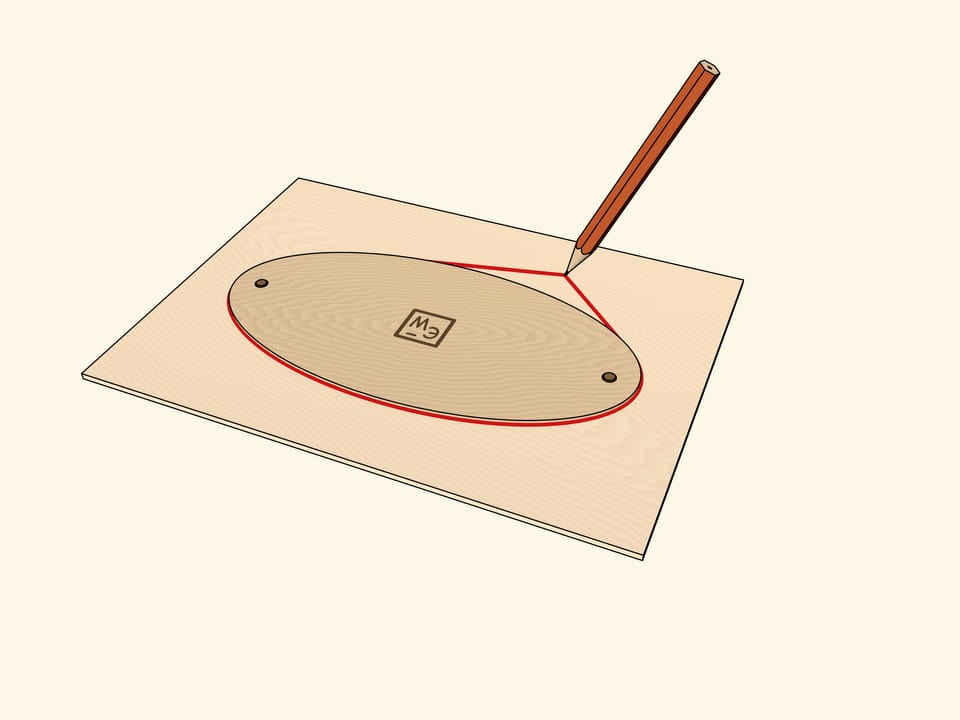
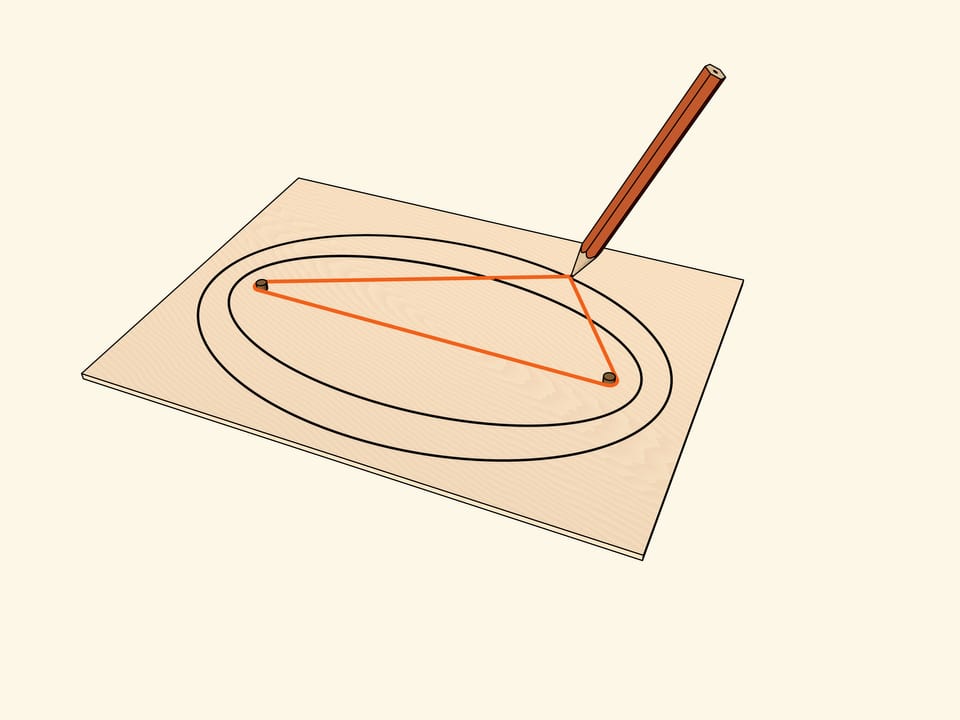
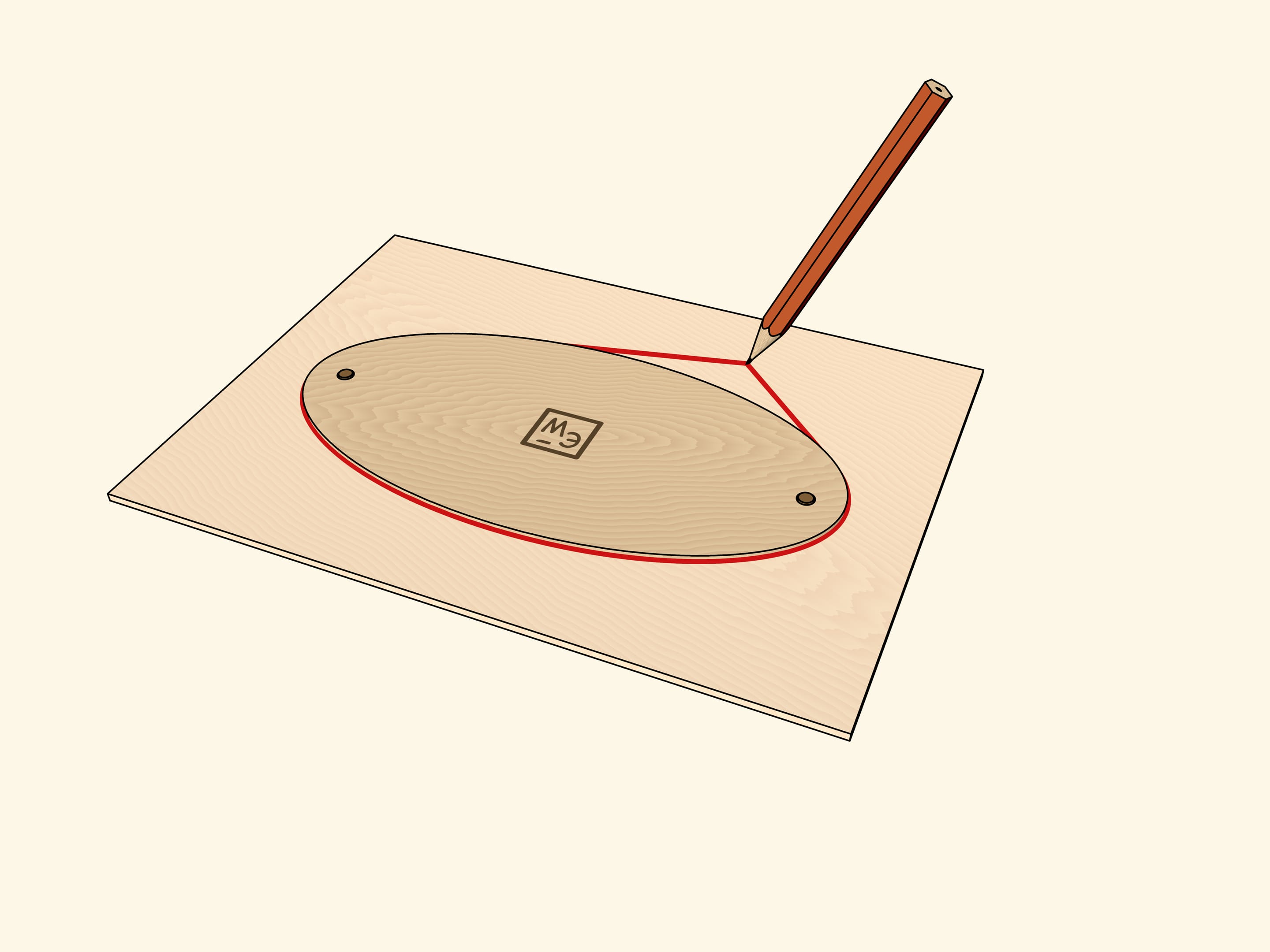
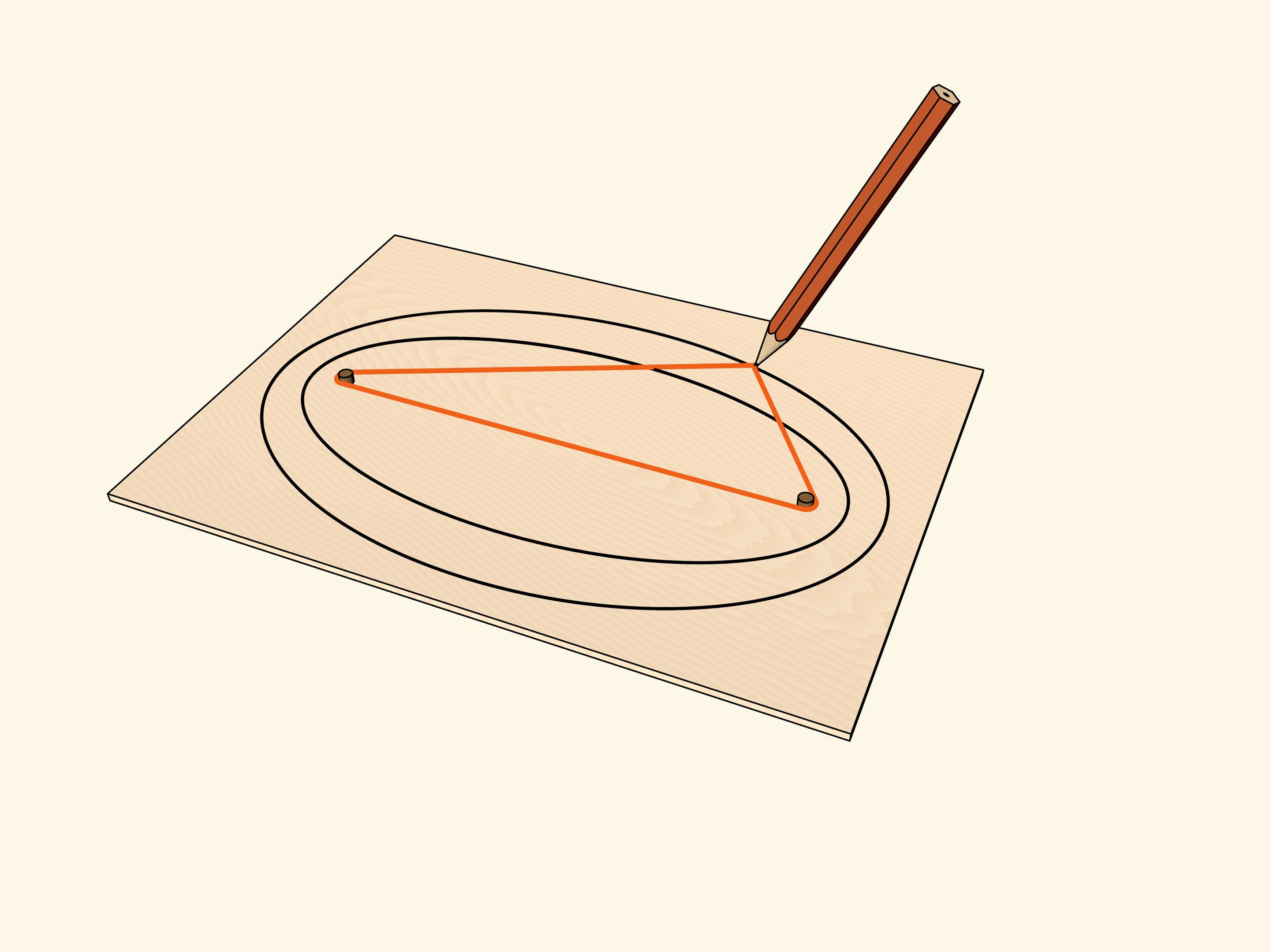
Взяв нить со свя­зан­ными кон­цами, охва­ты­вающую фокусы, и натя­нув её с помощью каран­даша, нари­суем эллипс. Нити раз­ной длины дают целое семейство софо­кус­ных эллип­сов. Но можно охва­ты­вать не отре­зок, соеди­няющий фокусы, а один из уже полу­чен­ных эллип­сов.

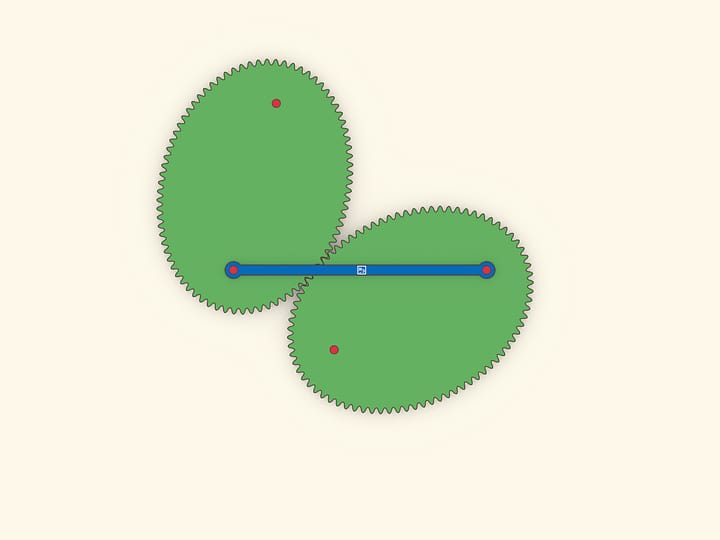
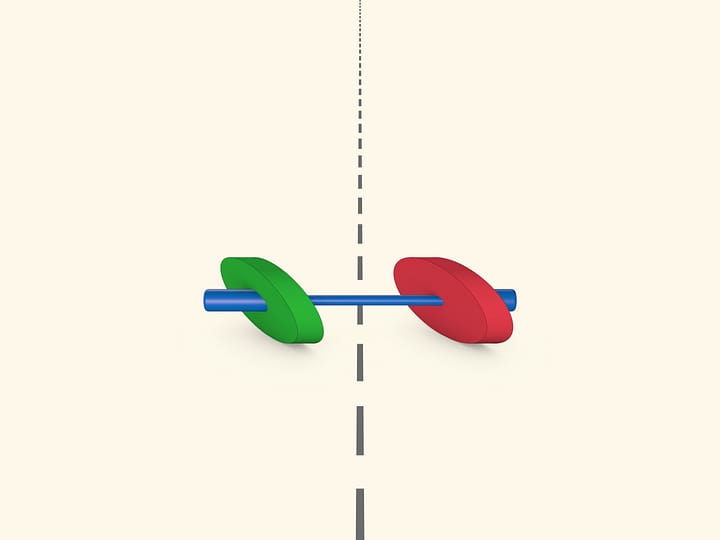
Нари­со­вав эллипс, изго­то­вим его «физи­че­скую» копию из доста­точно тол­стого мате­ри­ала, а затем совме­стим копию с ориги­на­лом. Возьмём нитя­ную петлю, кото­рой можно охва­тить эллипс, и, натя­нув её каран­дашом, про­ве­дём оваль­ную линию. Ока­зы­ва­ется, это тоже эллипс, при­чём софо­кус­ный исход­ному. Утвер­жде­ние можно про­ве­рить экс­пе­римен­тально, подо­брав длину петли, охва­ты­вающей фокусы.

Эту тео­рему в XIX веке дока­зал ирлан­дец Чарльз Грейвз, епи­скоп и матема­тик. В книге Феликса Клейна «Высшая геомет­рия» один из параграфов назы­ва­ется «Постро­е­ние из нитей Гревса и Шта­уде».

Дока­за­тельство тео­ремы Грей­вза мето­дами диффе­ренци­аль­ной геомет­рии можно про­чи­тать в книге Клейна. Отме­тим, что оно не явля­ется элемен­тар­ным, при­чина в том, что в каж­дый момент нить как линия состоит из двух отрез­ков, каса­тель­ных к эллипсу, и дуги эллипса. Уди­ви­тельно, но дуга эллипса — очень непро­стой объект, её длина выража­ется слож­ной форму­лой (исполь­зуются так назы­ва­емые эллип­ти­че­ские интегралы). А всего-то сжали окруж­ность, про кото­рую всё известно!

Известно «физи­че­ское» дока­за­тельство тео­ремы Грей­вза, осно­ван­ное на инту­и­тивно понят­ном утвер­жде­нии, что силы натяже­ния прямо­ли­ней­ных участ­ков нити равны. А вот суще­ствует ли дока­за­тельство на уровне элемен­тар­ной геомет­рии — без исполь­зо­ва­ния пре­де­лов и про­из­вод­ных — до сих пор неиз­вестно, и его пытаются найти многие геометры.