Качение эллипсов⁠

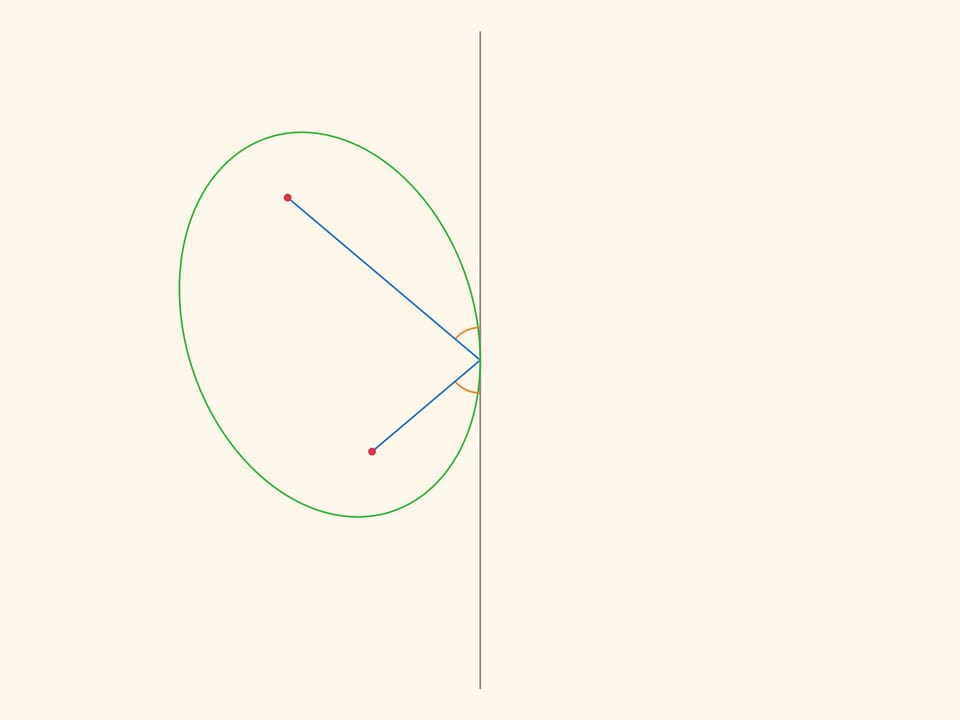
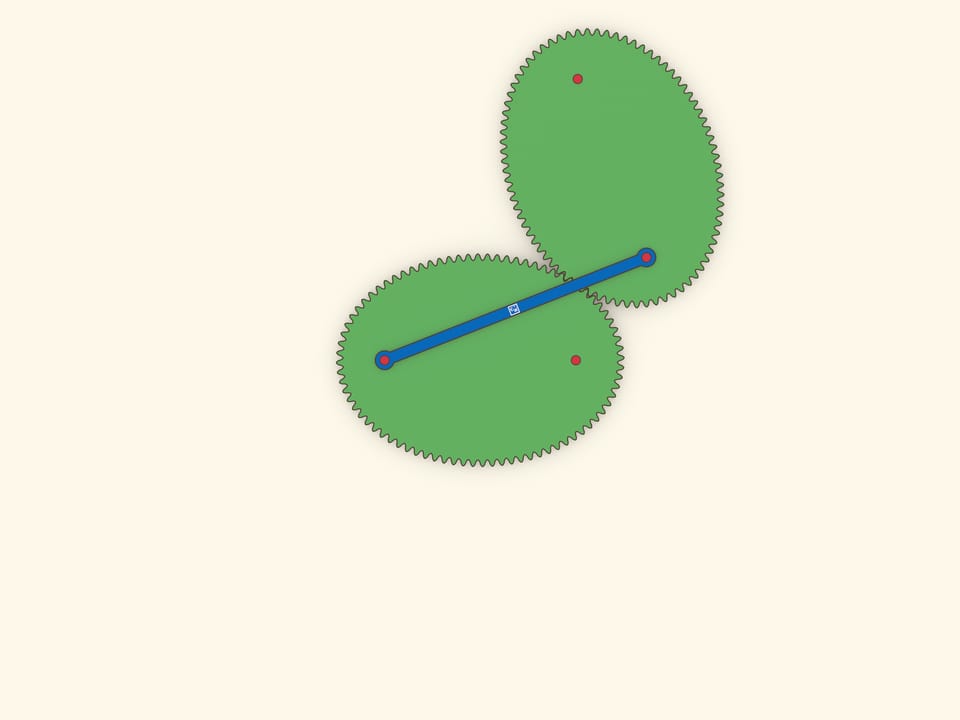
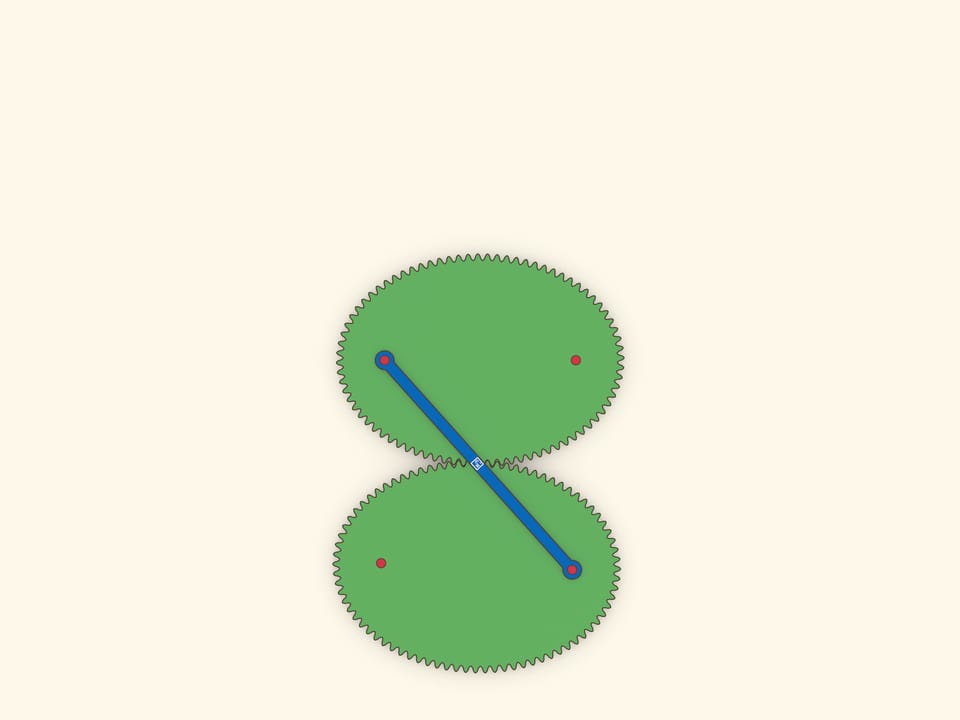
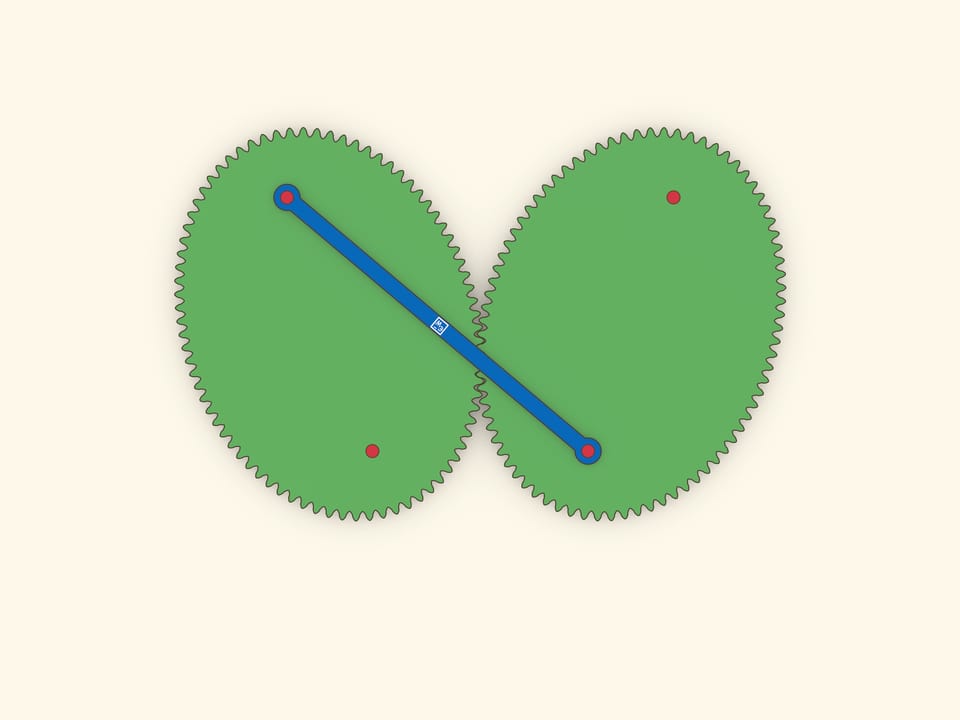
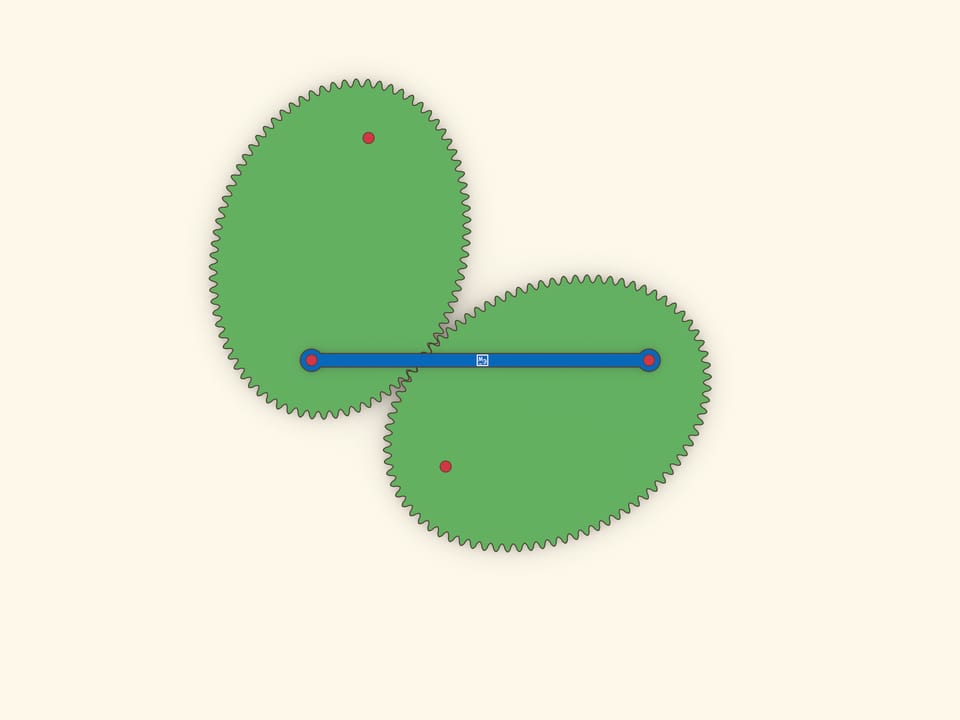
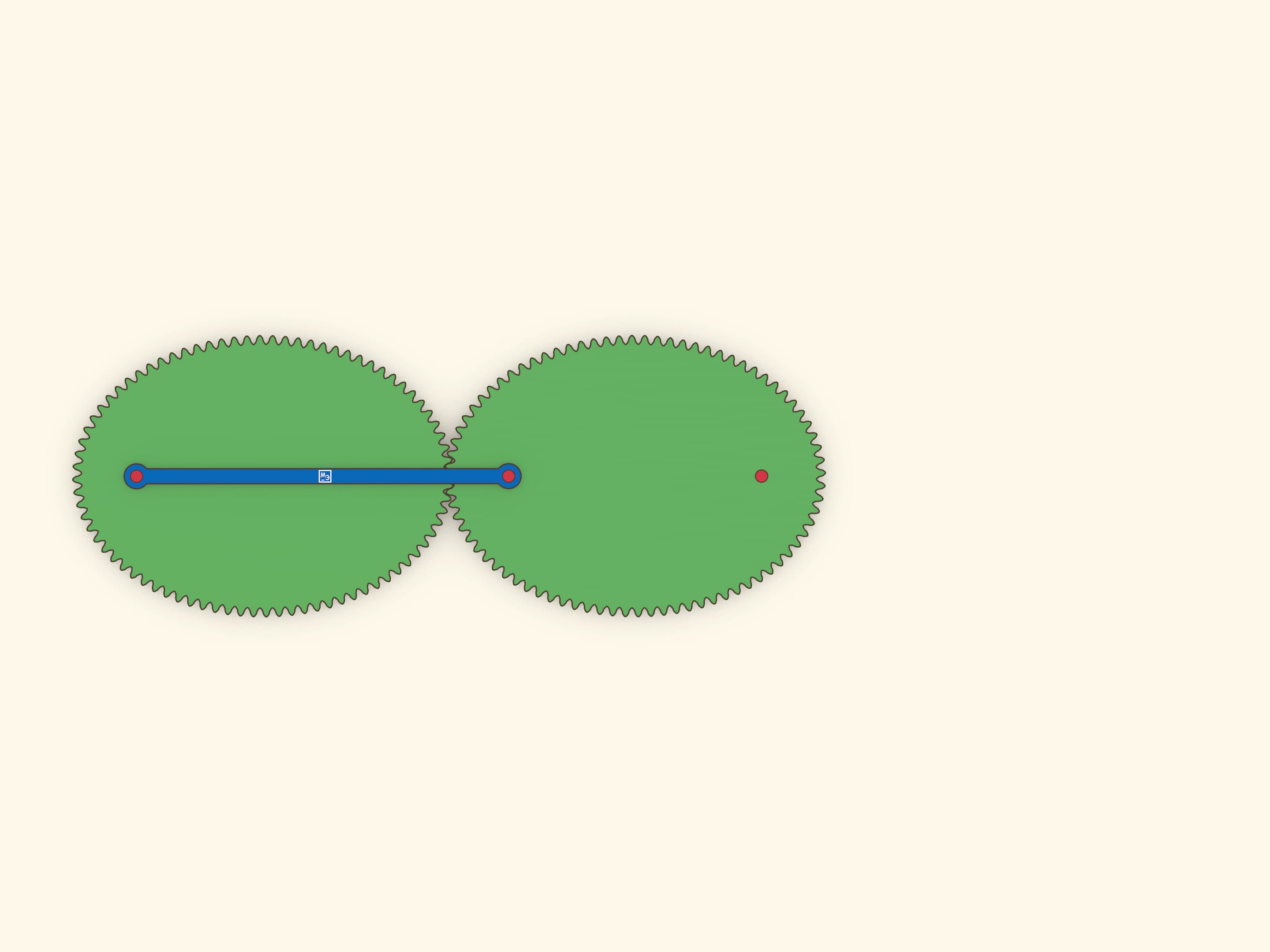
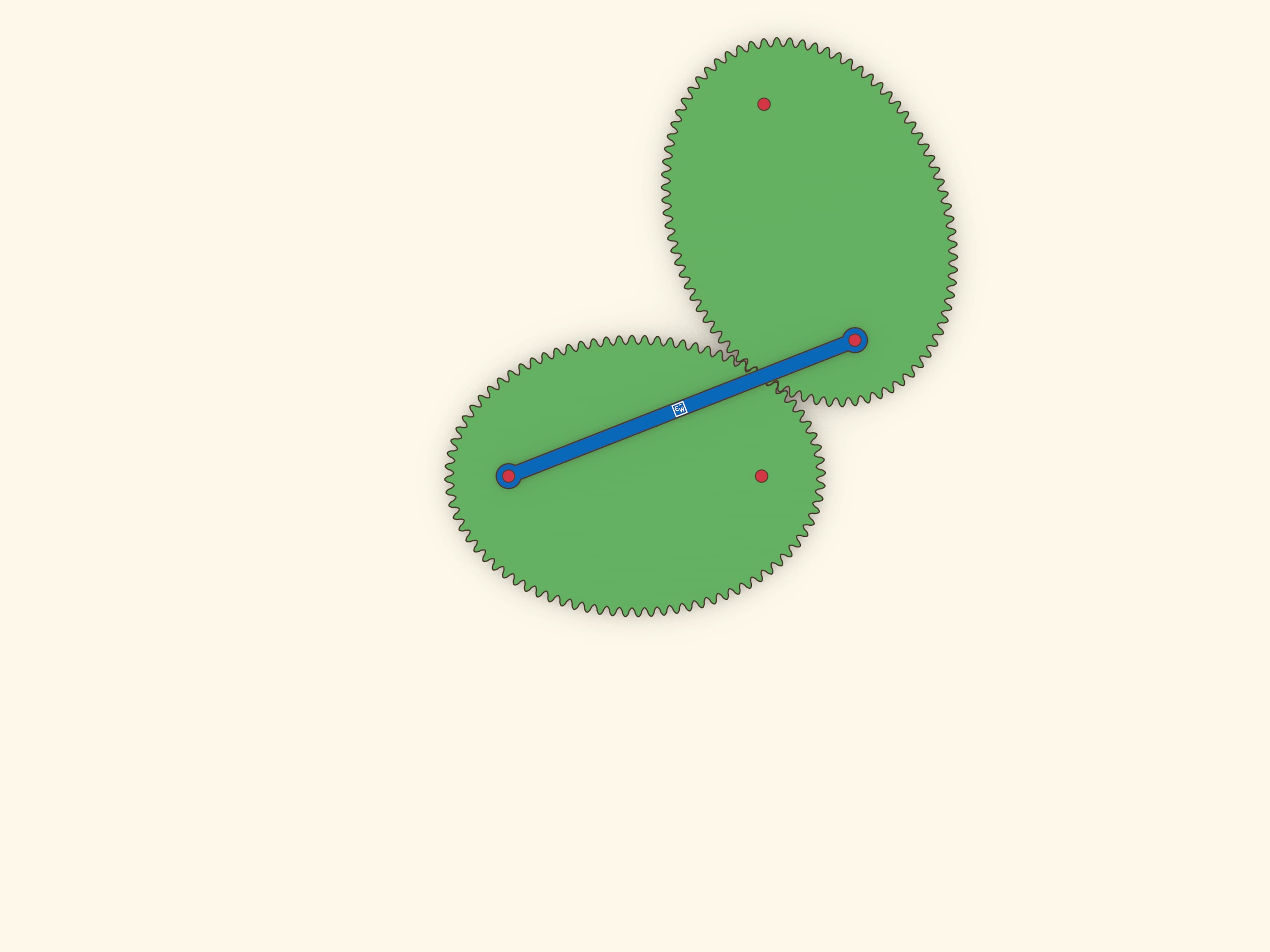
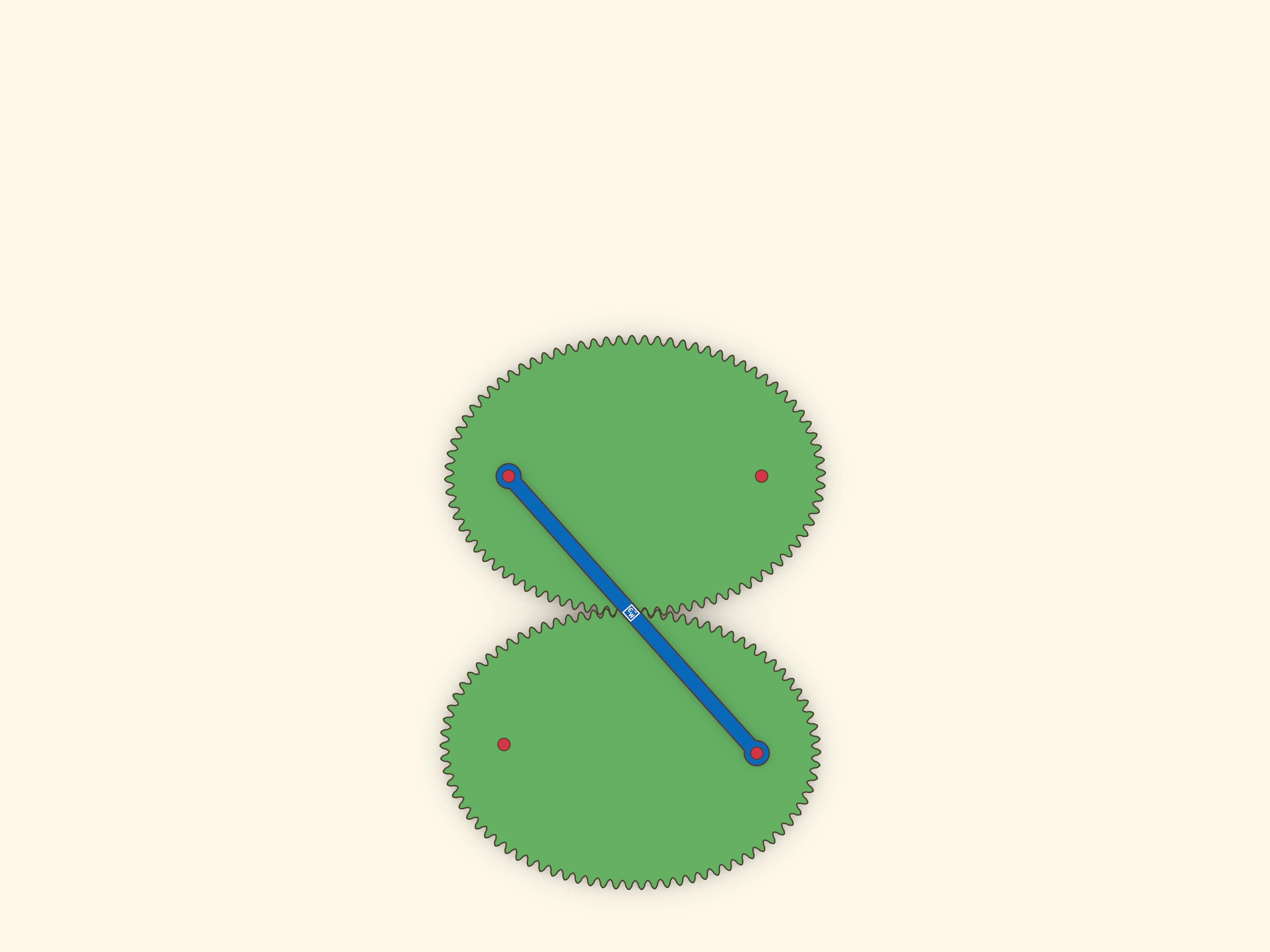
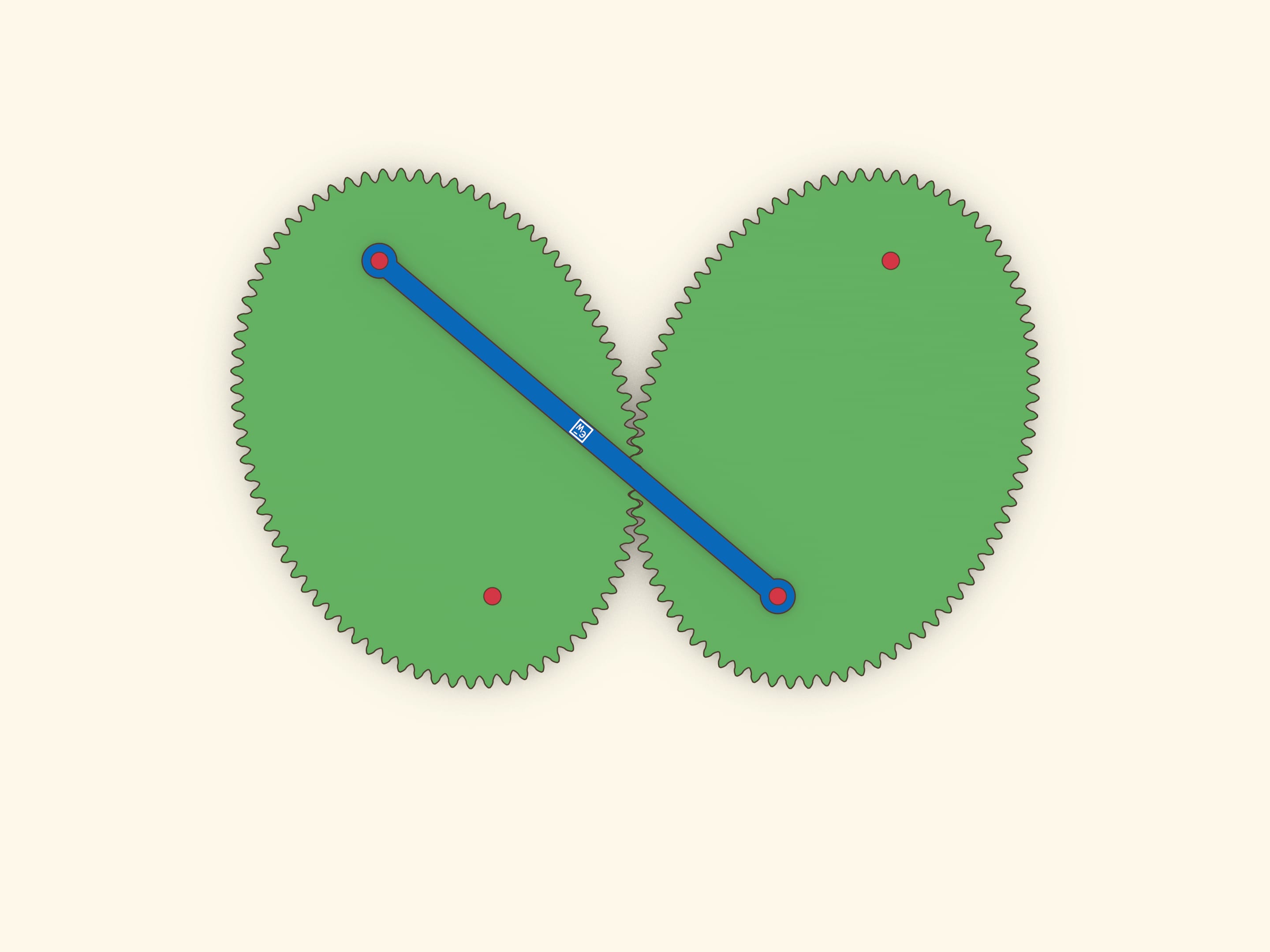
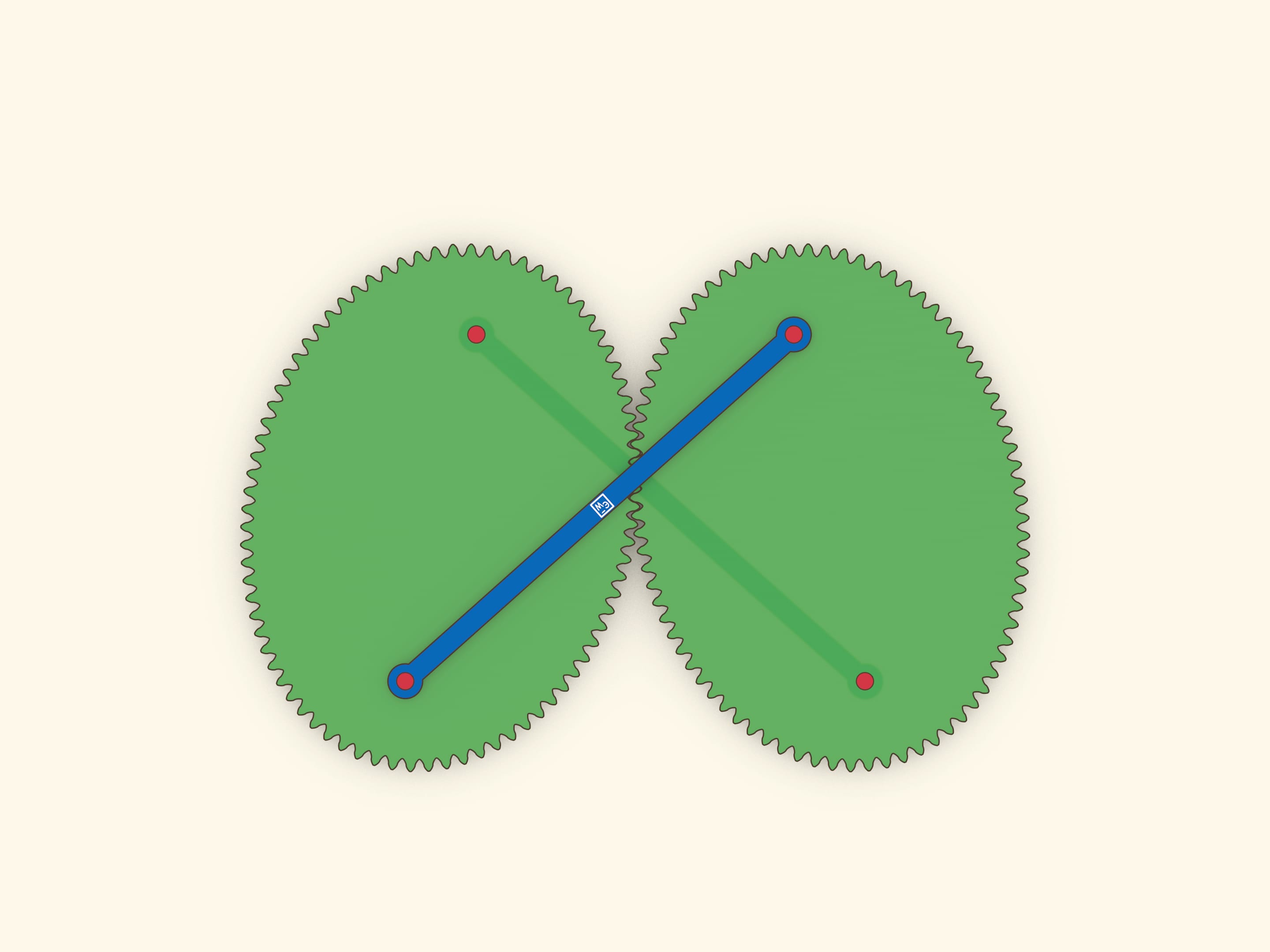
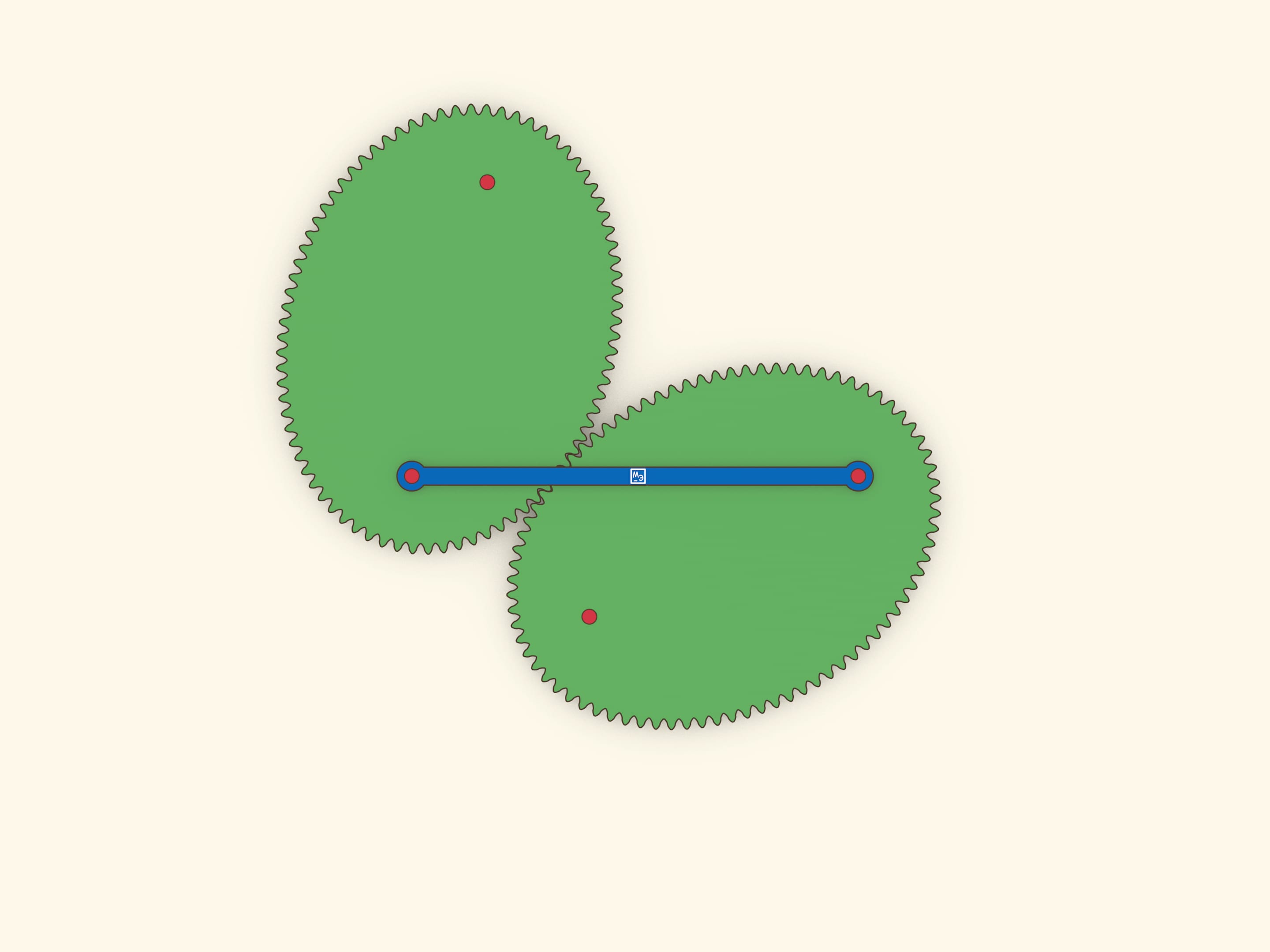
Опти­че­ское свойство эллипса гла­сит, что лучи, вышед­шие из одного фокуса, после отраже­ния от эллипса одно­временно при­дут во вто­рой фокус. Это свойство поз­во­ляет сде­лать про­стую, но заво­ражи­вающую модель: эллипс катится по рав­ному эллипсу, и при этом их фокусы соеди­нены план­кой, не меняющей длины.

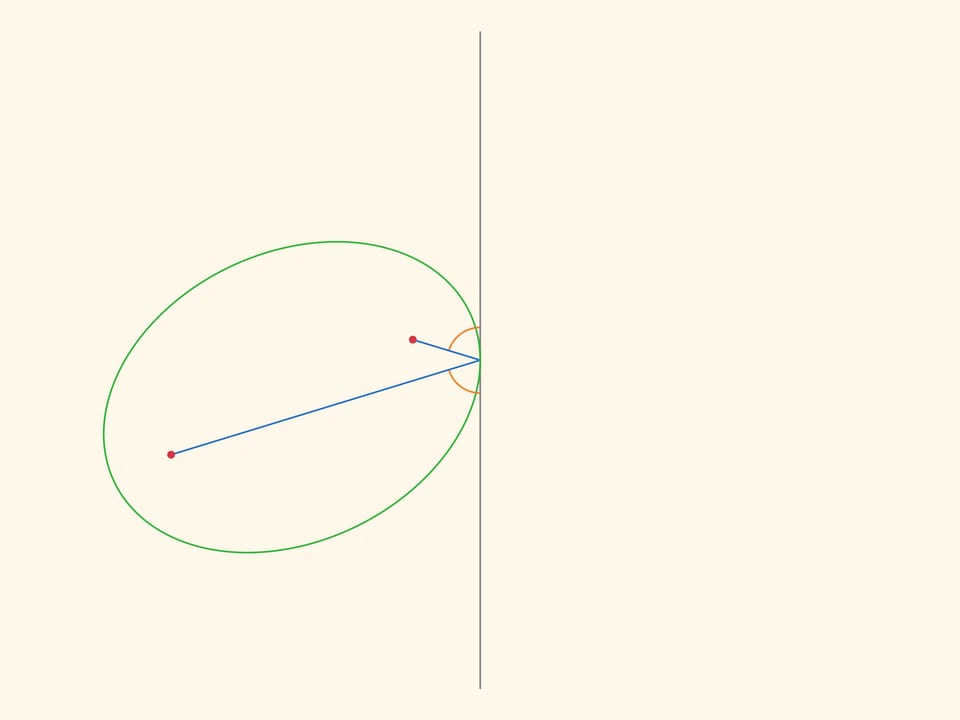
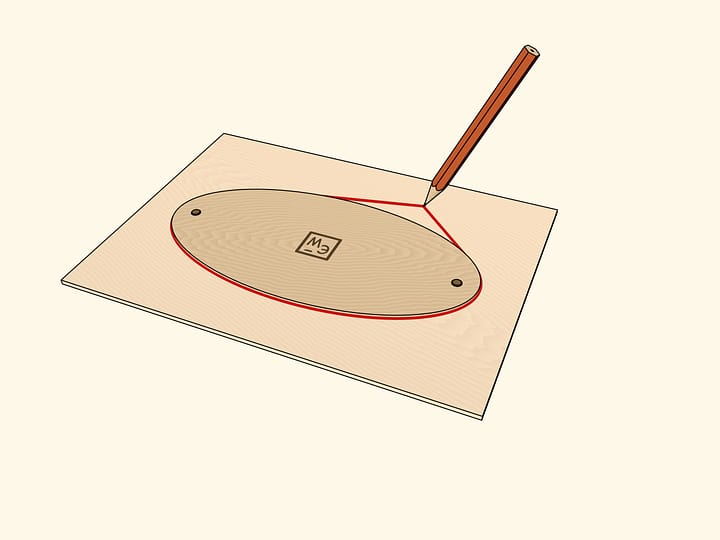
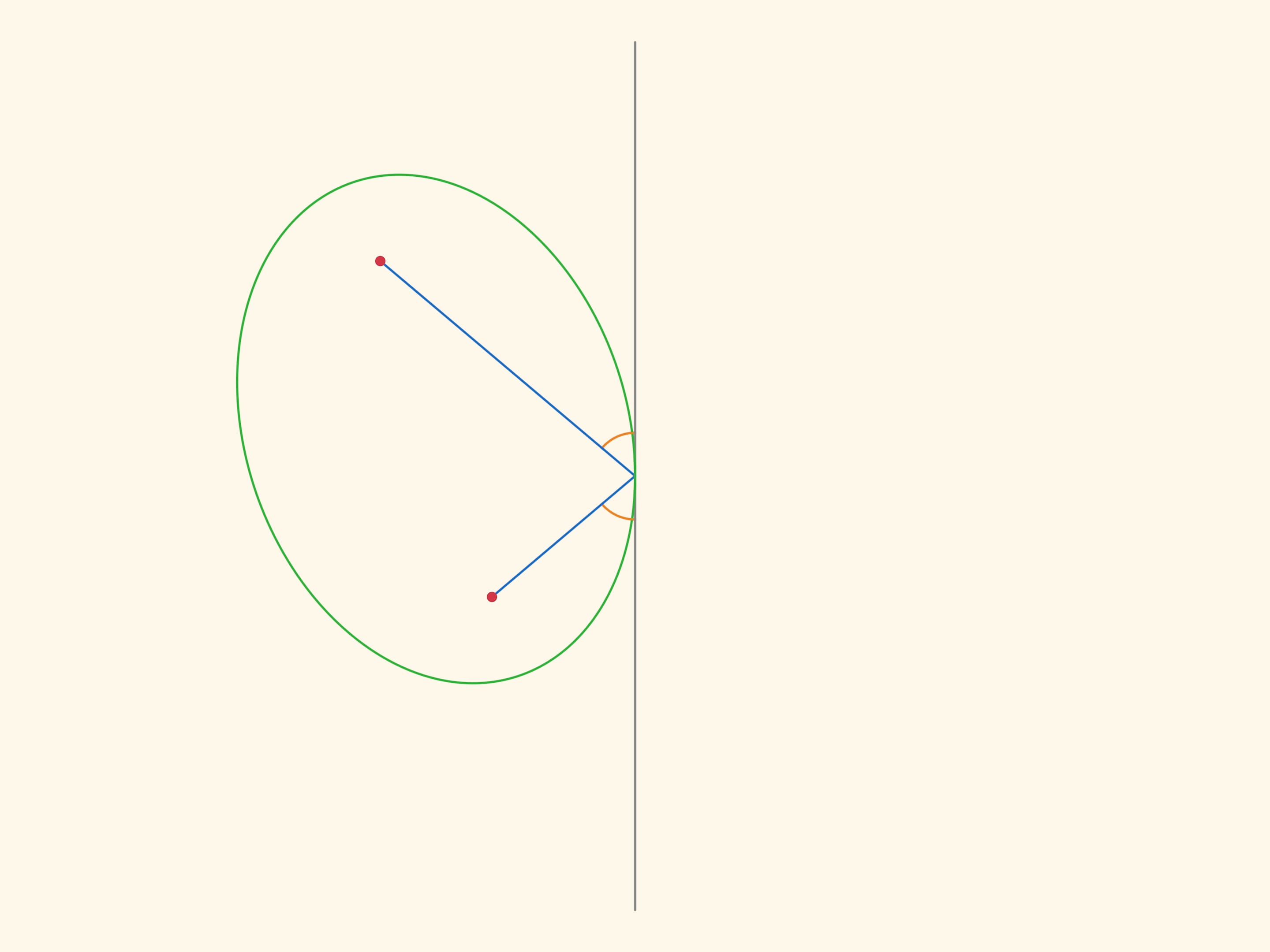
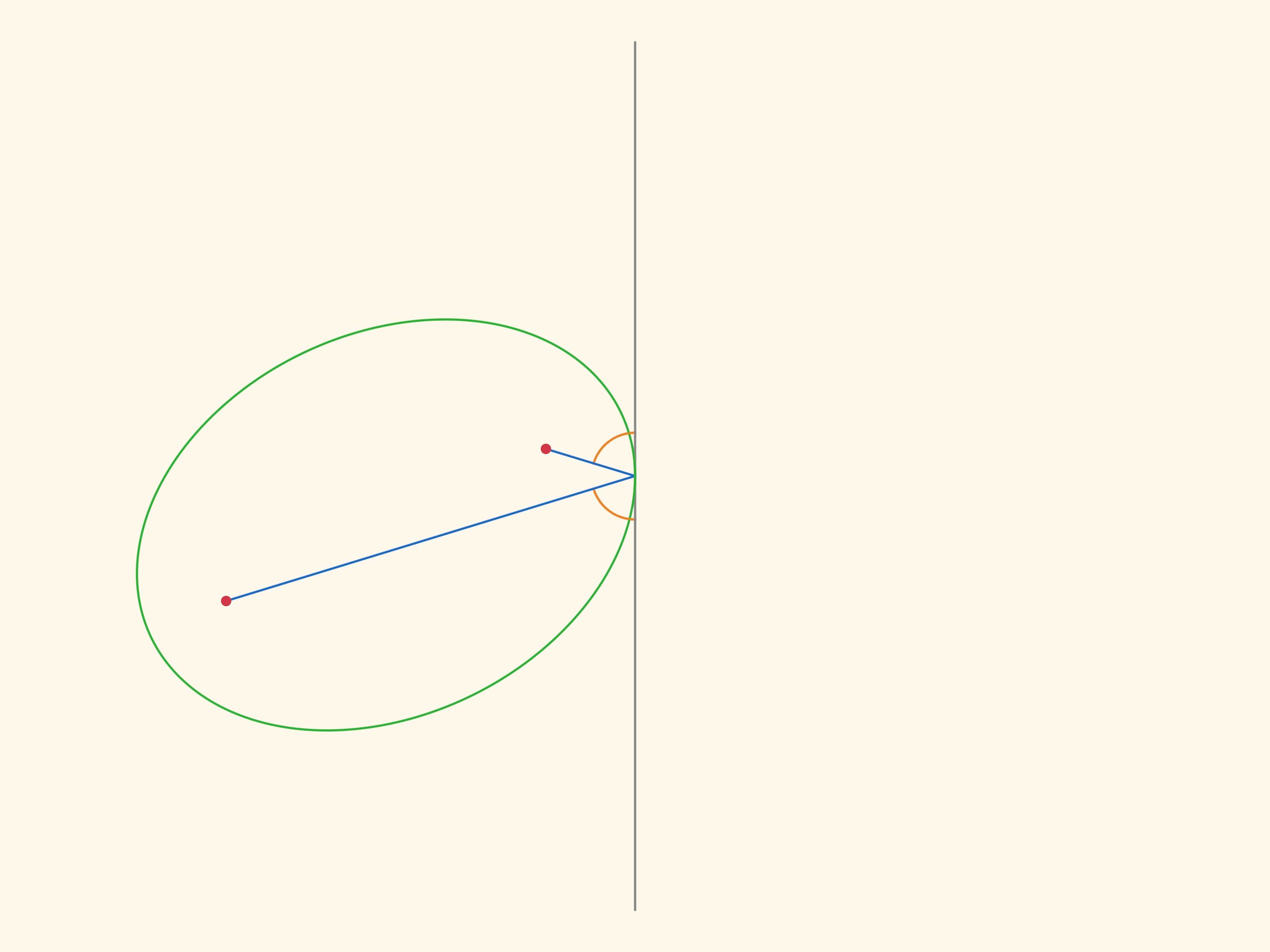
Опти­че­ским свойством обла­дают все кони­че­ские сече­ния: и эллипс, и пара­бола, и гипер­бола. При этом оно при­суще только им и в неко­то­ром смысле задаёт их, могло бы являться их опре­де­ле­нием. Но ⁠⁠для эллипса опти­че­ское свойство дока­зы­ва­ется проще всего: верё­вочка, выри­со­вы­вающая эллипс, все­гда состав­ляет оди­на­ко­вые углы с каса­тель­ной.

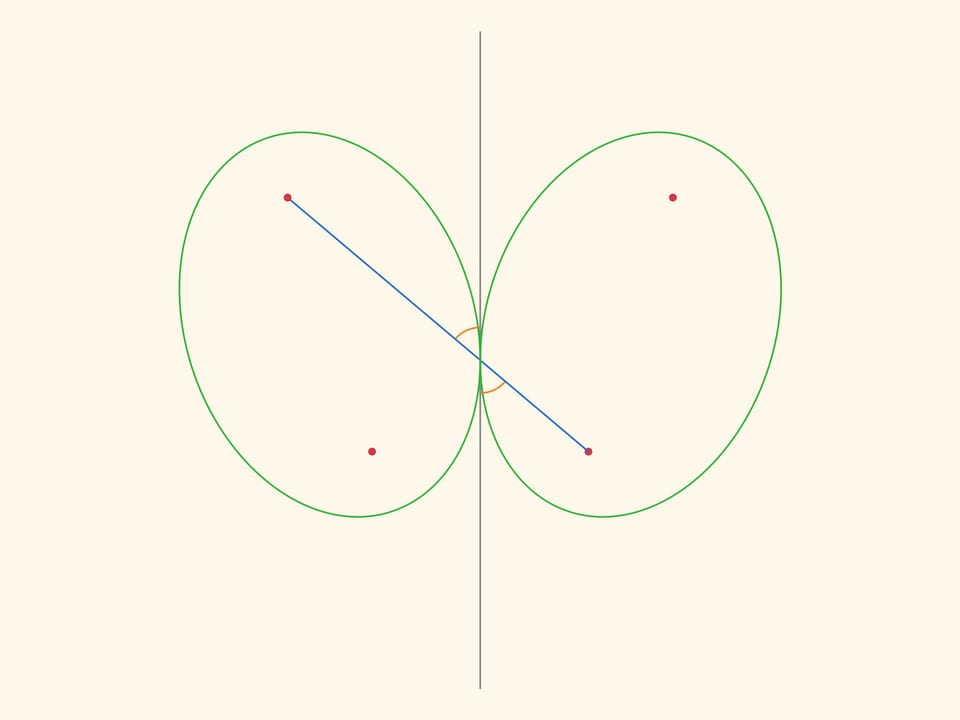
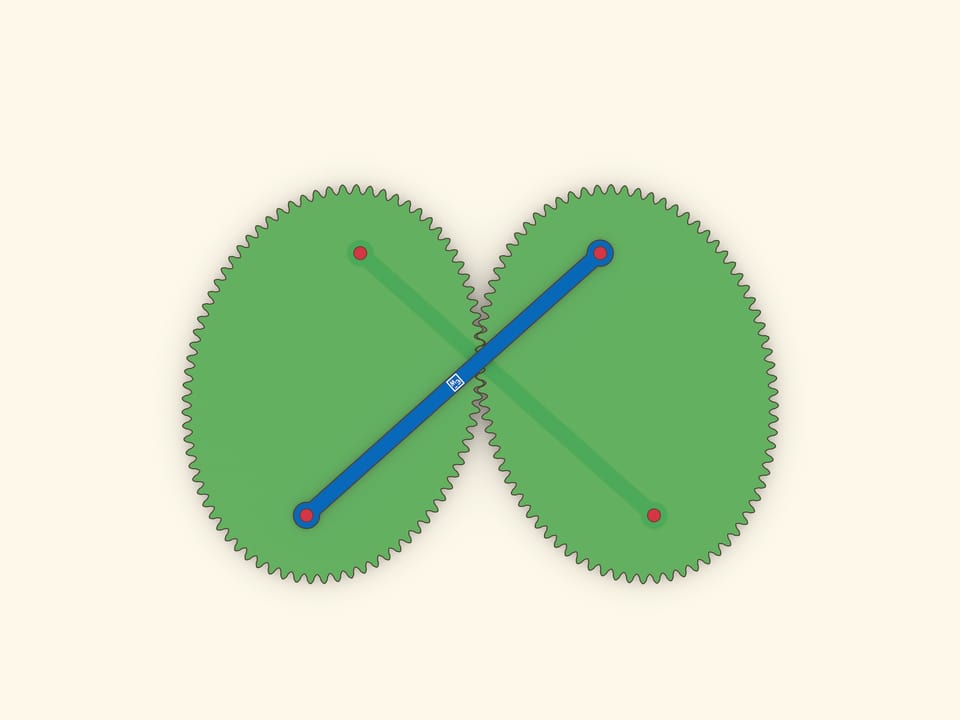
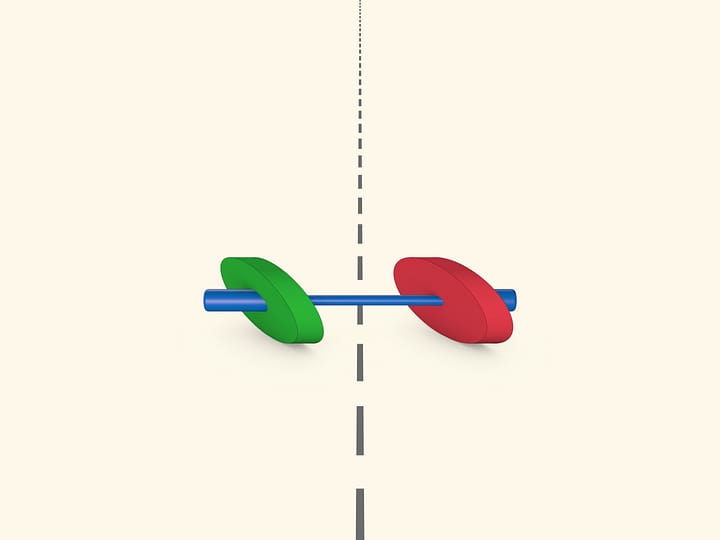
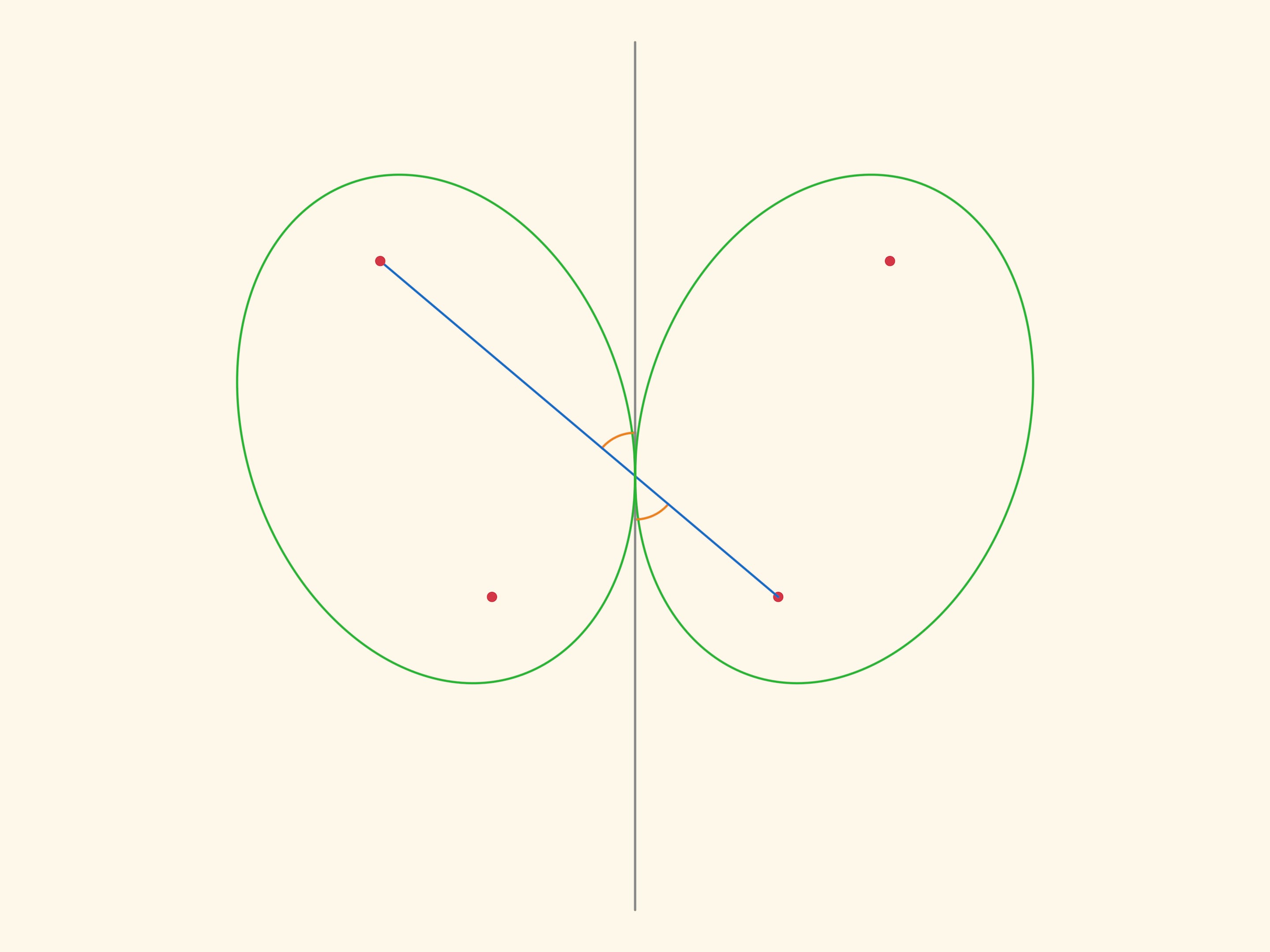
Отра­зим эллипс отно­си­тельно каса­тель­ной. В силу опти­че­ского свойства, рас­сто­я­ние между «накрест лежащими» фоку­сами не меня­ется, и их можно соеди­нить план­кой. Если один эллипс непо­движ­ный, то каж­дый из фоку­сов вто­рого ходит по окруж­но­сти.

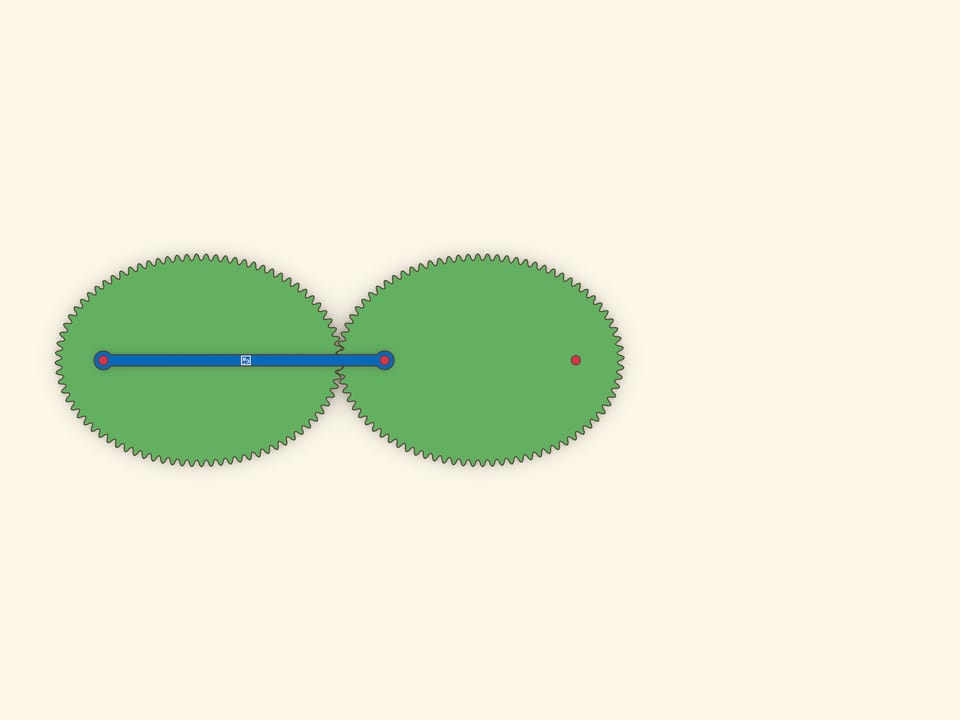
Чтобы эллипсы не про­скаль­зы­вали при каче­нии одного по другому, необ­хо­димо сде­лать зуб­ча­тое зацеп­ле­ние. Тео­рия постро­е­ния профи­лей зуб­ча­тых зацеп­ле­ний — нетри­ви­аль­ная наука. В нашей модели исполь­зо­ва­лись гипо- и эпицик­ло­иды, постро­ен­ные на эллипсе.