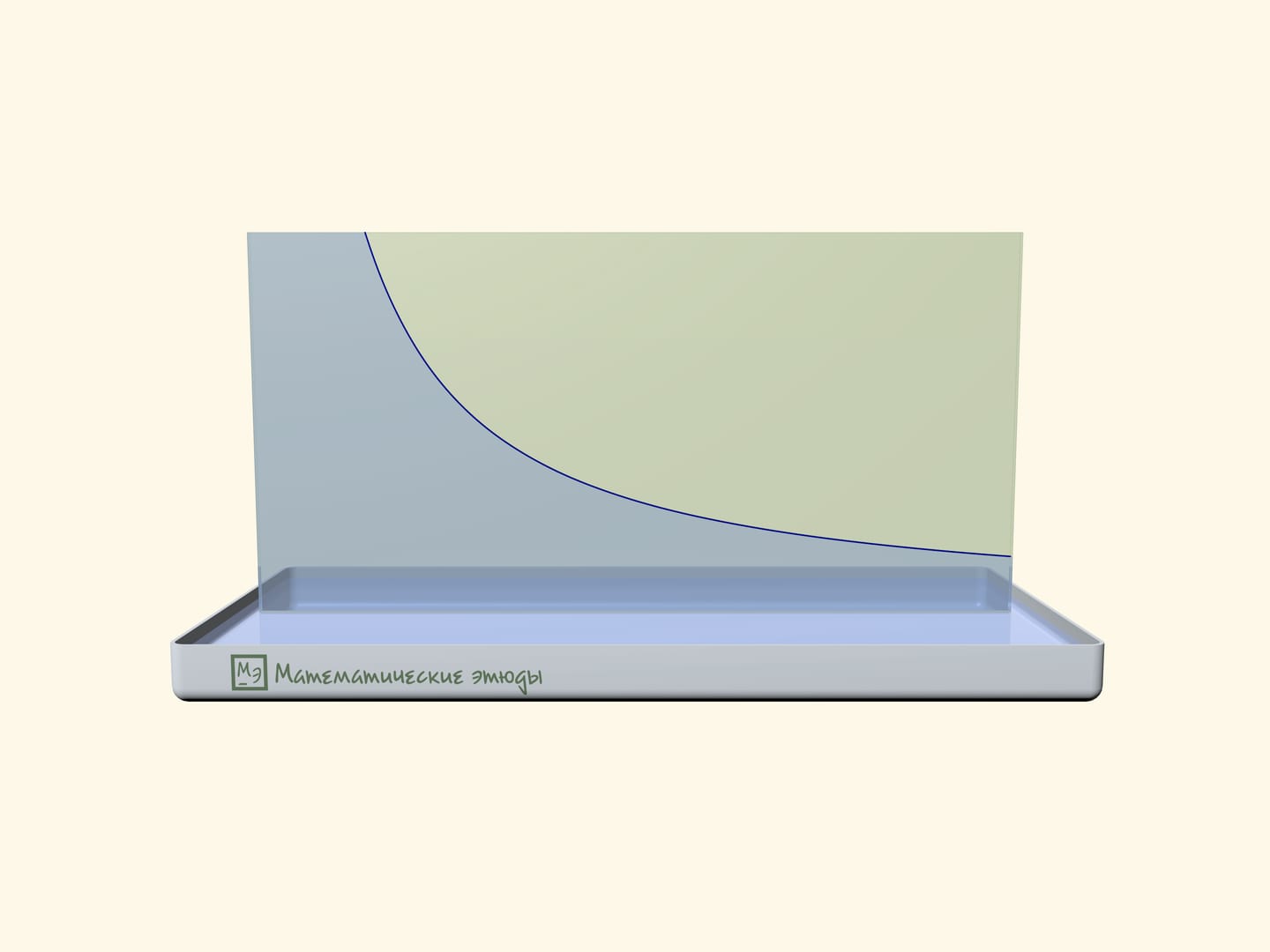
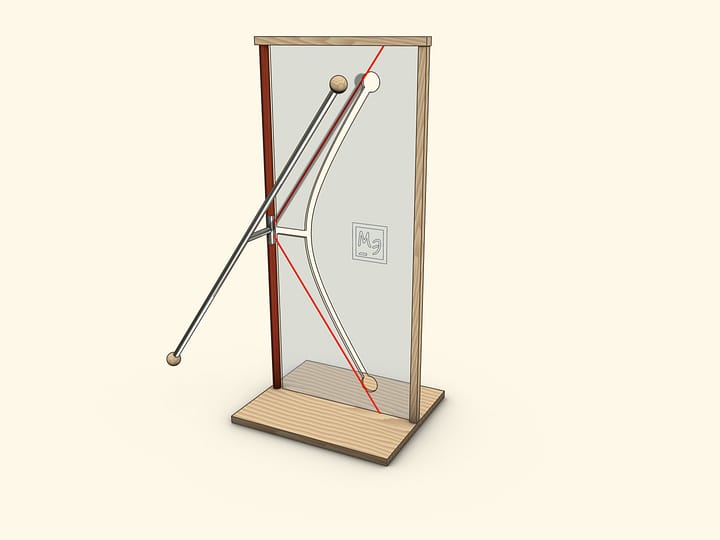
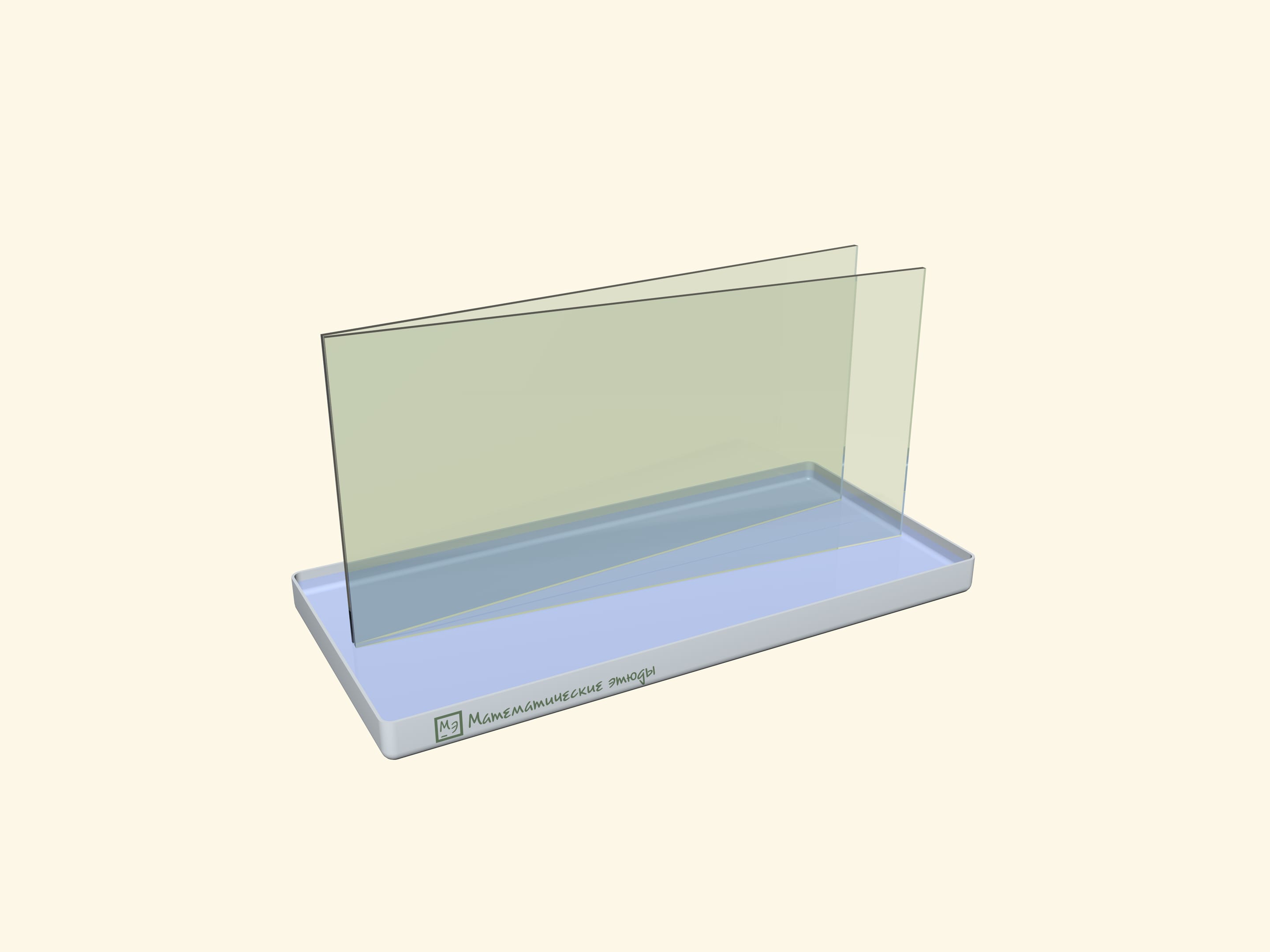
Гиперболу в домашних условиях могут «нарисовать» силы поверхностного натяжения.
В ванночку с водой поставьте две прямоугольные стеклянные пластинки в виде слегка приоткрытой книги. Начните медленно закрывать «книгу»: вода между пластинками поднимется, а её уровень будет снижаться по знакомой кривой — гиперболе (начинающейся с некоторым отступом от «корешка книги»).
Физическое объяснение описанного эксперимента читатель может получить самостоятельно, а может найти в журнале «Квант».
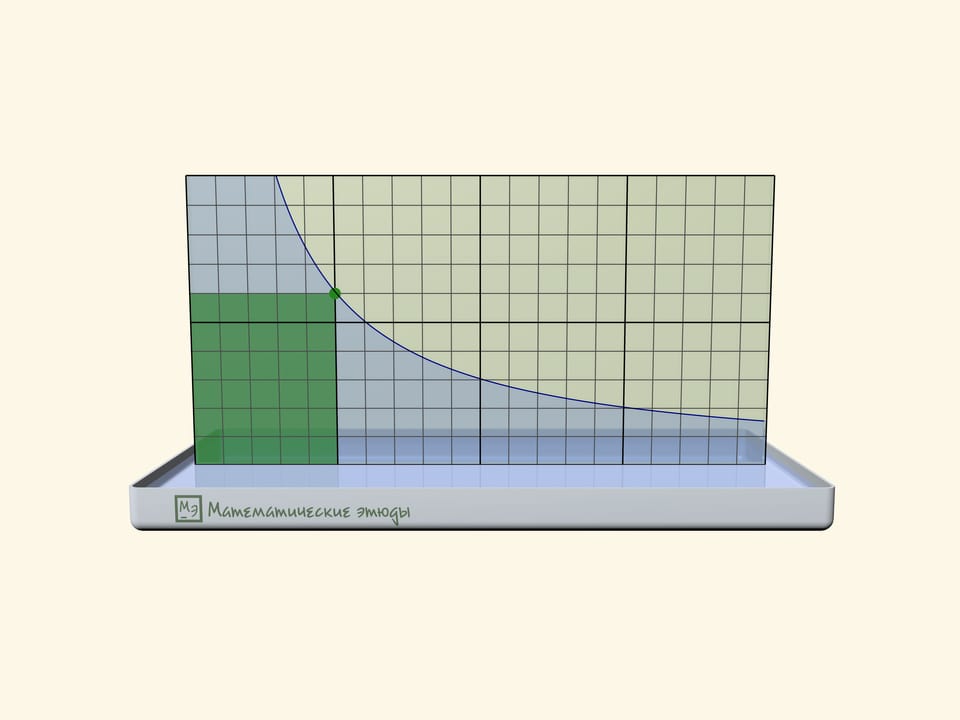
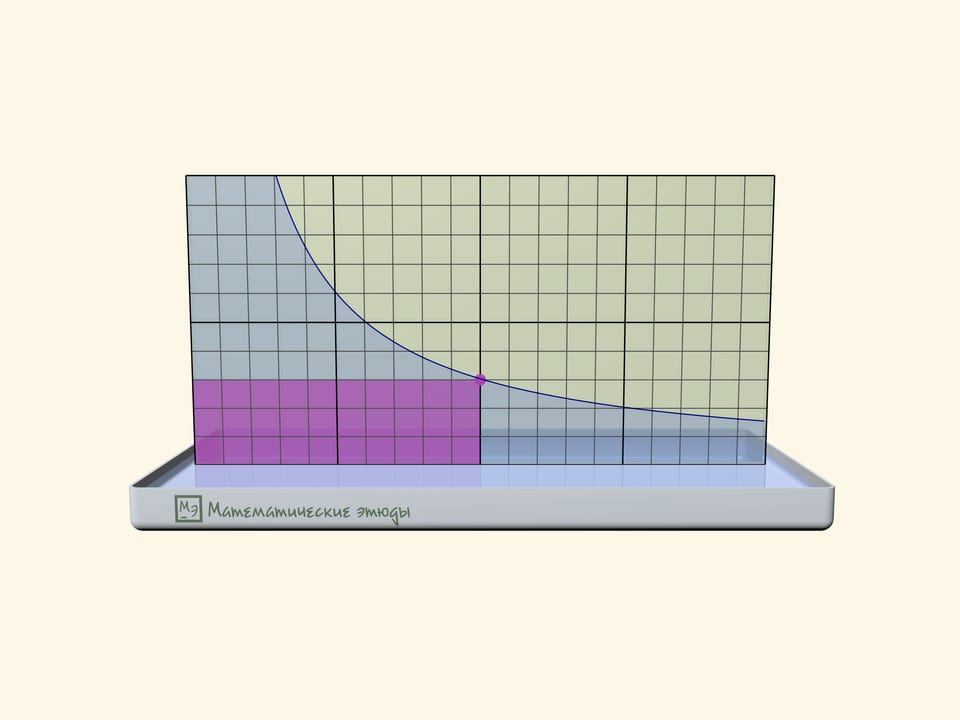
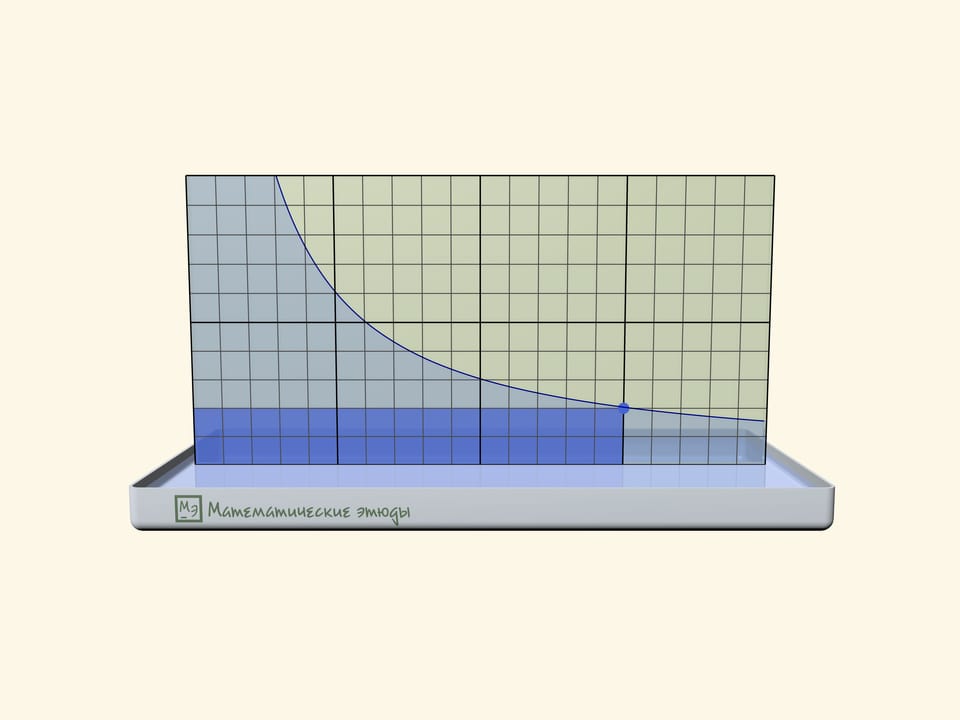
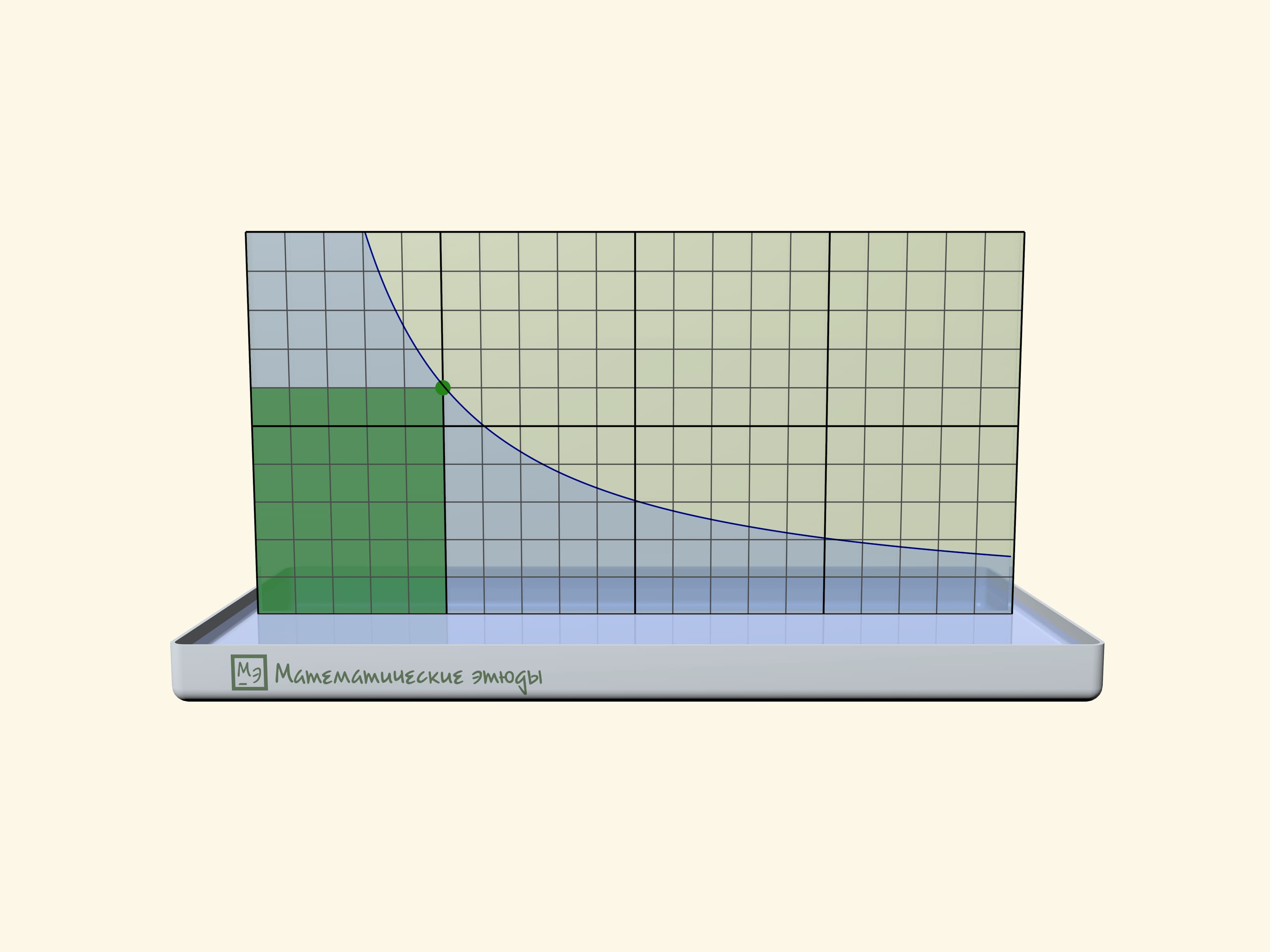
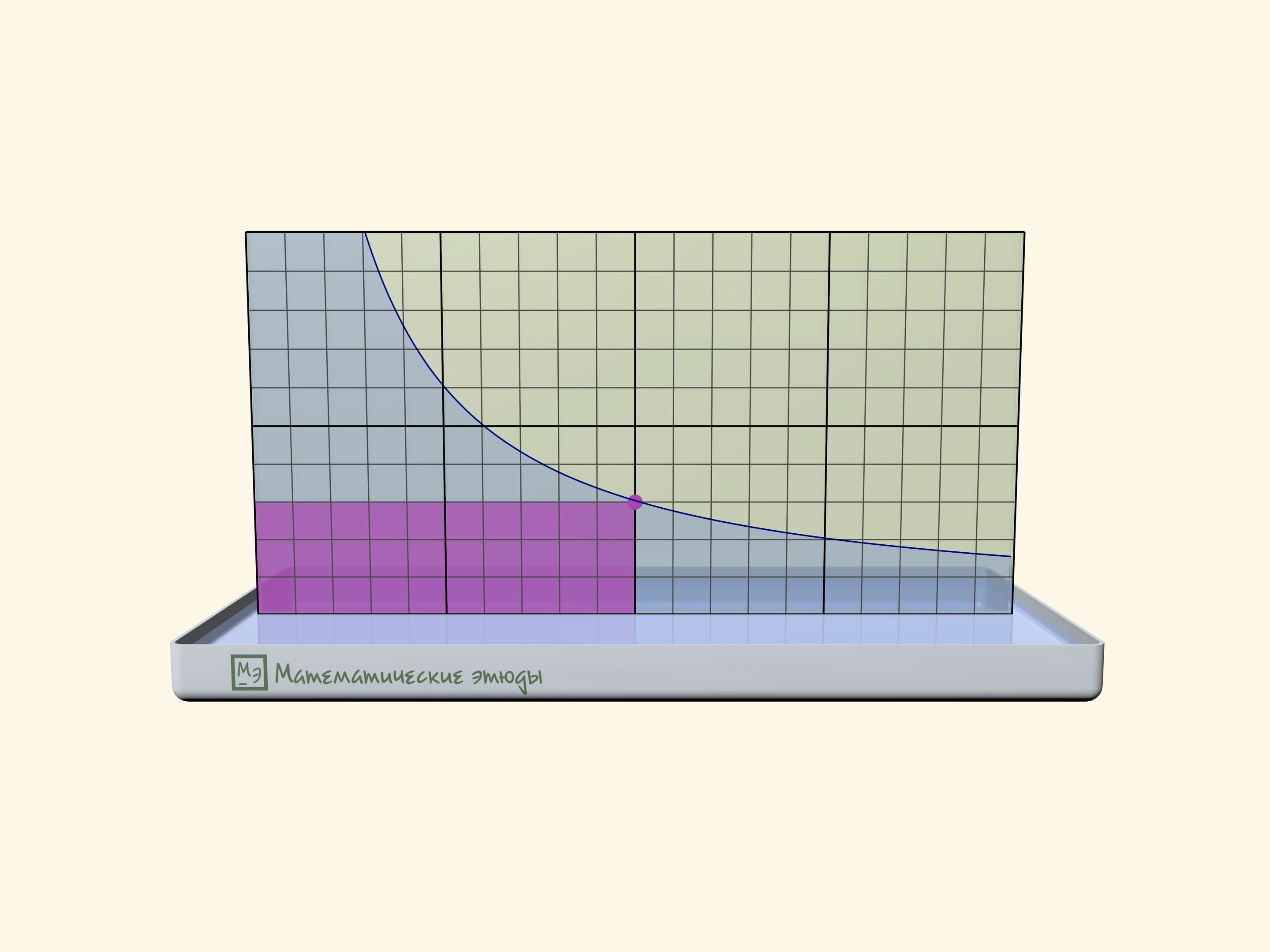
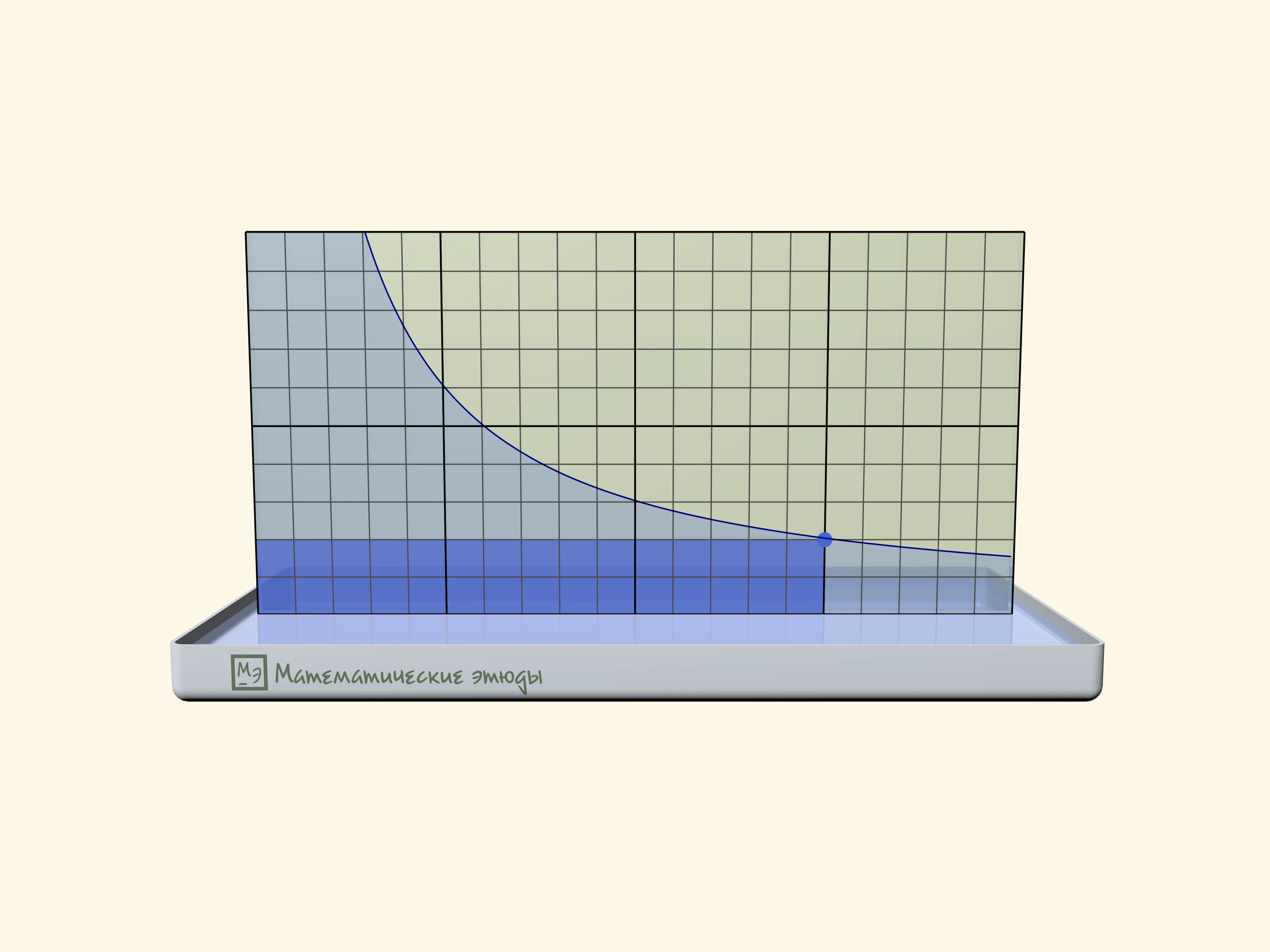
Если предварительно на одном стёклышке нарисовать мелкую квадратную сетку, то можно проверить, что получилась именно гипербола: площади прямоугольников под линией будут одинаковыми.
Прямоугольники под гиперболой стали основой задачи, впервые возникшей на Московской математической олимпиаде 2020 года:
На графике функции $y=1/x$ Миша отмечал подряд все точки с абсциссами $1$, $2$, $3$, …, пока не устал. Потом пришла Маша и закрасила все прямоугольники, одна из вершин которых — это отмеченная точка, еще одна — начало координат, а еще две лежат на осях. Затем учительница попросила ребят посчитать площадь фигуры, состоящей из всех точек, закрашенных ровно один раз. Сколько получилось?
Ответ, что площадь равна в точности $1$, не зависит от того, сколько точек отметил Миша, и может быть получен как алгебраически, так и геометрически.
Литература
Воробьёв И. И. Поверхностное натяжение чертит гиперболу // Журнал «Квант». 1973. № 11. Стр. 32—33.
Шуховские башни // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 88—89, 322—325.