Образующие гиперболоида ⁠

⁠⁠Одно­по­лост­ный гипер­бо­лоид враще­ния — поверх­ность, обра­зо­ван­ная враще­нием гипер­болы вокруг её мнимой оси (оси симмет­рии, перпен­ди­ку­ляр­ной отрезку с кон­цами в фоку­сах).

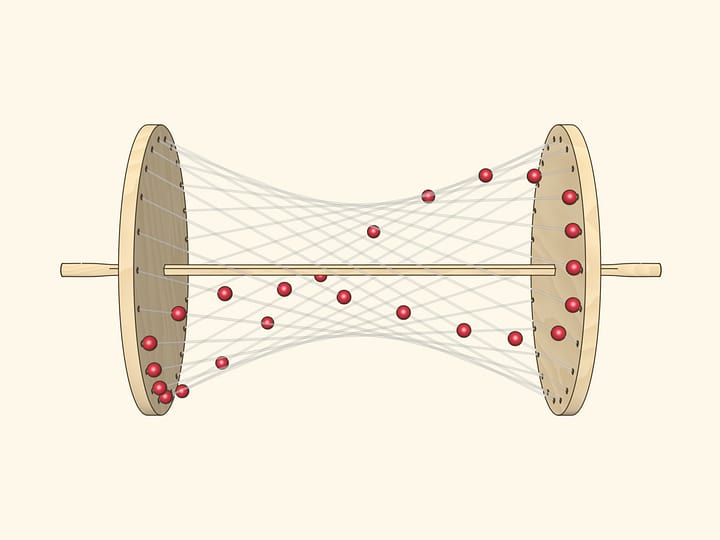
Через каж­дую точку гипер­бо­ло­ида про­хо­дят две прямые, пол­но­стью лежащие на нём. Каж­дая из них при враще­нии вокруг оси гипер­бо­ло­ида «заме­тает» всю поверх­ность. Такие линии назы­ваются обра­зующими. Обра­зующие делятся на два семейства: в одно семейство попа­дают те обра­зующие, кото­рые при враще­нии вокруг оси пере­хо­дят друг в друга. Пред­ста­вить обра­зующие одно­по­лост­ного гипер­бо­ло­ида можно с помощью раз­лич­ных моде­лей.

Более про­стая для изго­тов­ле­ния модель исполь­зует про­зрач­ный цилиндр (напри­мер, акри­ло­вый), два круга-донышка с отвер­сти­ями, через кото­рые про­дета резинка. Пово­ра­чи­вая один круг отно­си­тельно другого, наблю­да­тель видит раз­лич­ные одно­по­лост­ные гипер­бо­ло­иды. Небольшой недо­ста­ток этой модели — меня­ется длина обра­зующих.

Самую про­стую и попу­ляр­ную модель можно сде­лать из шпажек (напри­мер, для шаш­лыка) и небольших кольце­вых рези­но­чек (для пле­те­ния). Можно полу­чать как симмет­рич­ные гипер­бо­ло­иды, так и со смещён­ной «талией». Самое слож­ное в изго­тов­ле­нии этой модели — про­думать после­до­ва­тель­ность соеди­не­ний.

На стек­лян­ном одно­по­лост­ном гипер­бо­ло­иде прямо­ли­ней­ные обра­зующие могут быть про­де­мон­стри­ро­ваны с помощью света. Благо он не может выйти из более опти­че­ски плот­ной среды (стекла) в менее плот­ную (воз­дух). Кстати, огром­ное коли­че­ство дио­дов уста­нов­лено на отре­ста­ври­ро­ван­ной башне Шухова под Ниж­ним Новго­ро­дом, и вече­ром она пере­ли­ва­ется раз­ными цве­тами.

Уви­деть большой кра­си­вый одно­по­лост­ный гипер­бо­лоид, состав­лен­ный из прямо­ли­ней­ных обра­зующих, можно, побы­вав рядом с одной из башен, постро­ен­ных Вла­ди­ми­ром Григо­рье­ви­чем Шухо­вым. Всего их было постро­ено более 200, ⁠⁠и часть из них сохра­ни­лась.