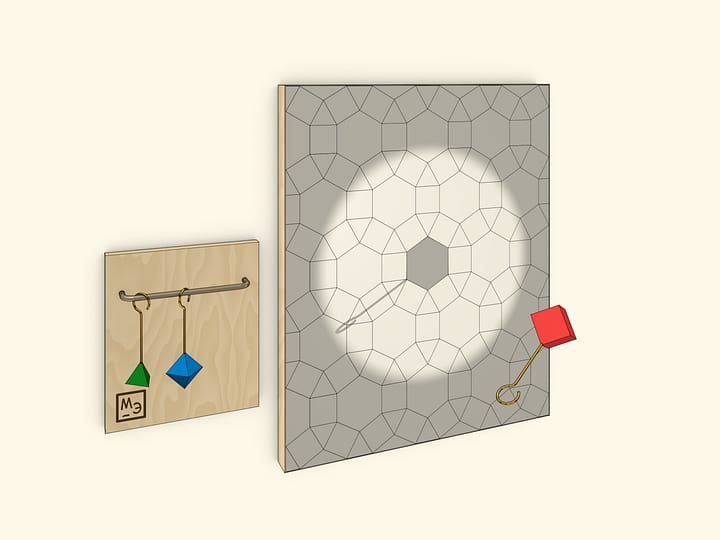
Правильные многогранники естественным образом связаны друг с другом. Это и двойственность правильных многогранников, и всевозможные варианты вписать один многогранник в другой. И тем не менее явная встреча с этой взаимосвязью иногда удивляет.
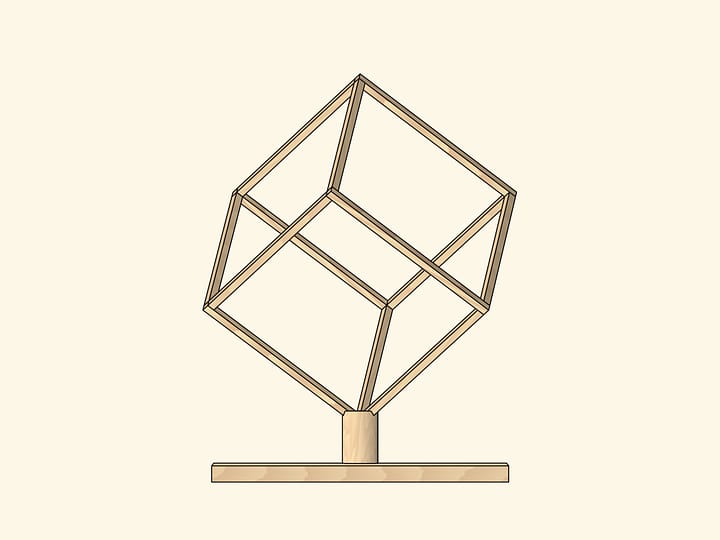
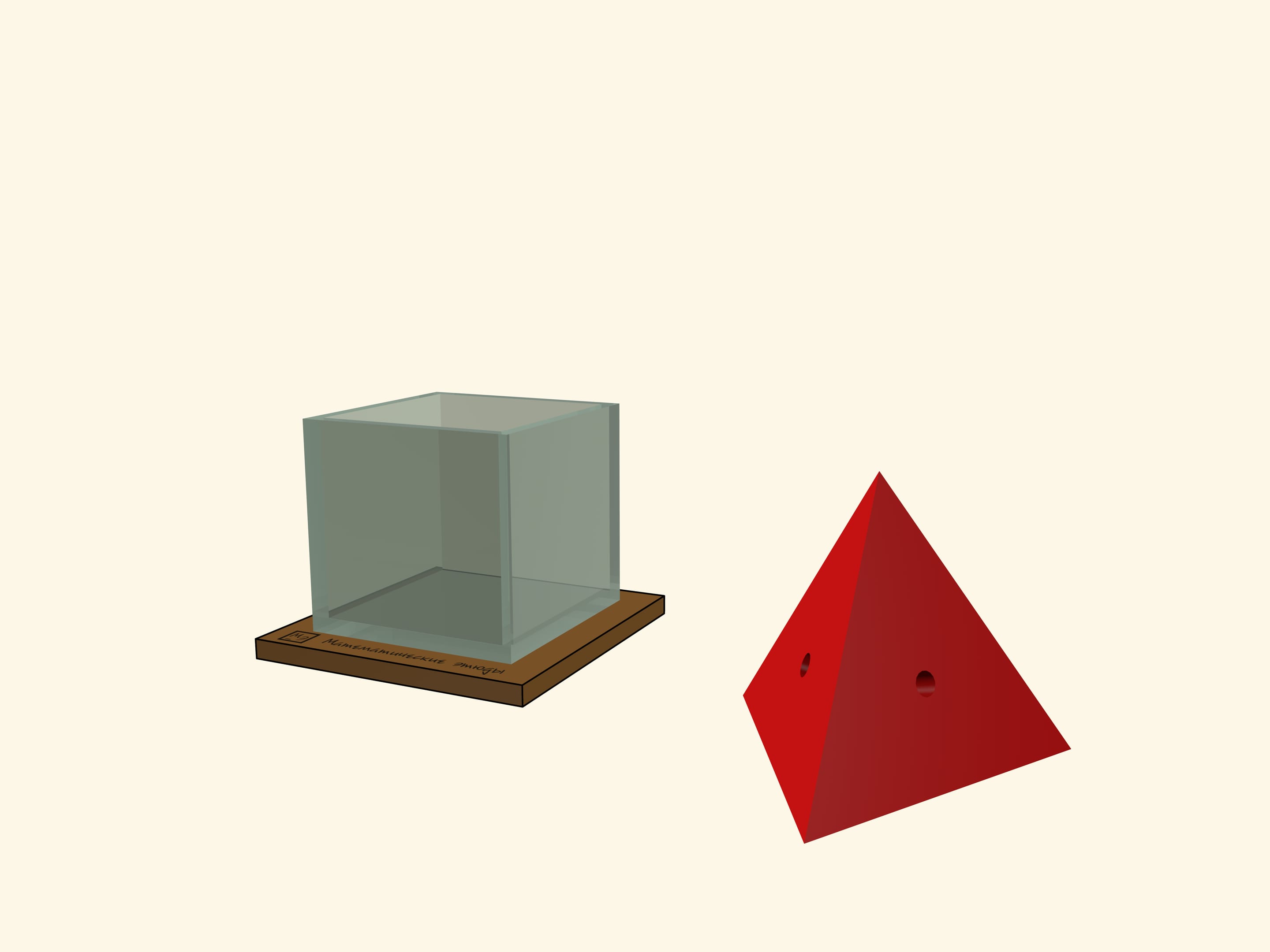
Основой модели, которая поражает и детей, и взрослых, служит куб без верхней грани, сделанный из стекла или акрила. В комплект входит несколько многогранников, которые лучше вырезать из лёгкого, например вспененного, материала. В случае, если размеры куба большие, то в многогранниках, соответствующих по размеру кубу, стоит предусмотреть отверстия для пальцев.
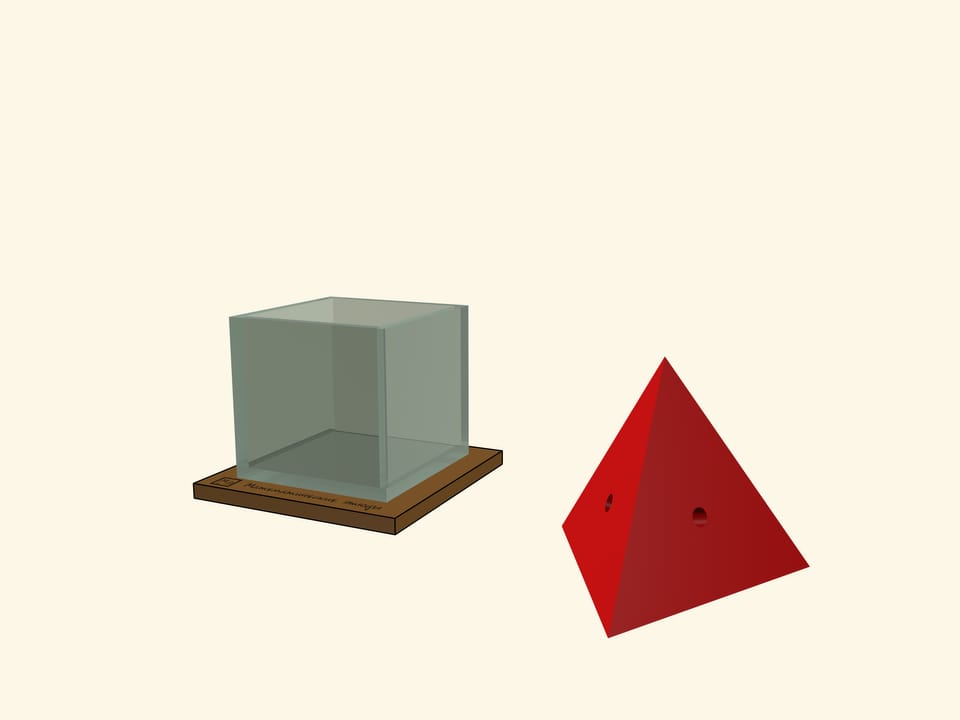
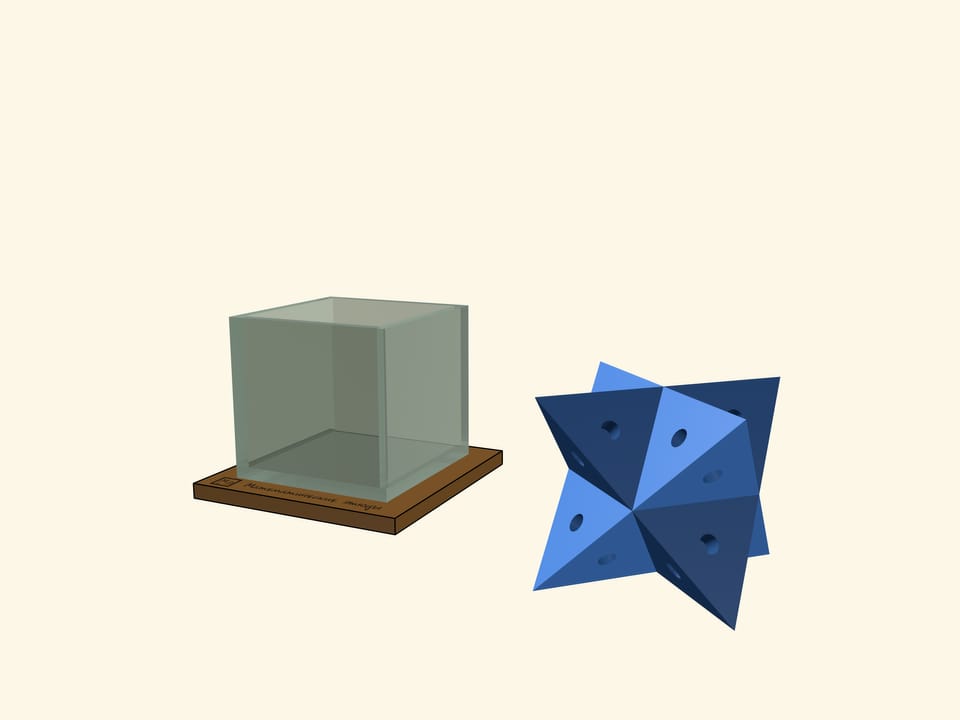
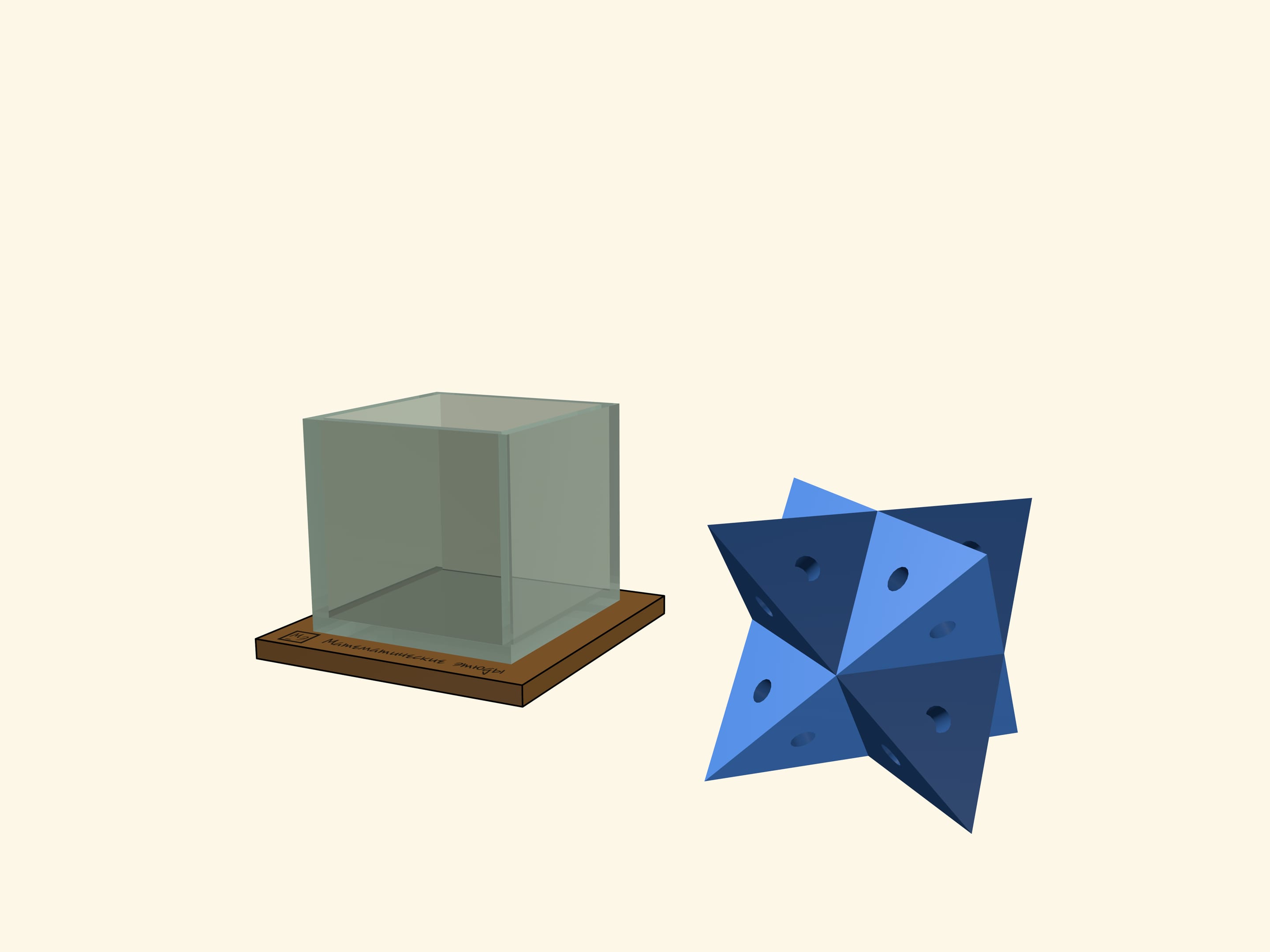
Самым удивительным многогранником, который можно поместить в куб, является «большой» тетраэдр. На первый взгляд он никак не может поместиться внутри, но это если не знать, что тетраэдр может быть вписан в куб так, чтобы все вершины тетраэдра совпадали с вершинами куба. В качестве вариации можно взять два «противоположных» тетраэдра. Такой многогранник — объединение этих тетраэдров — рассматривал Иоганн Кеплер и дал ему название «stella octangula».
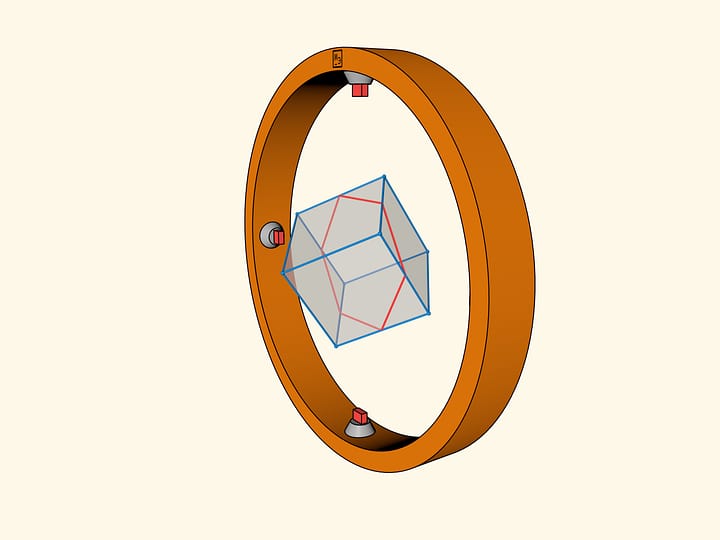
Пересечением куба и двойственного ему октаэдра, увеличенного так, чтобы их рёбра пересекались, является кубооктаэдр. Этот полуправильный многогранник появляется и в фильмах Star Trek, и в компьютерной игре Elite. Будучи получен как усечение куба, он может быть помещён внутрь него.
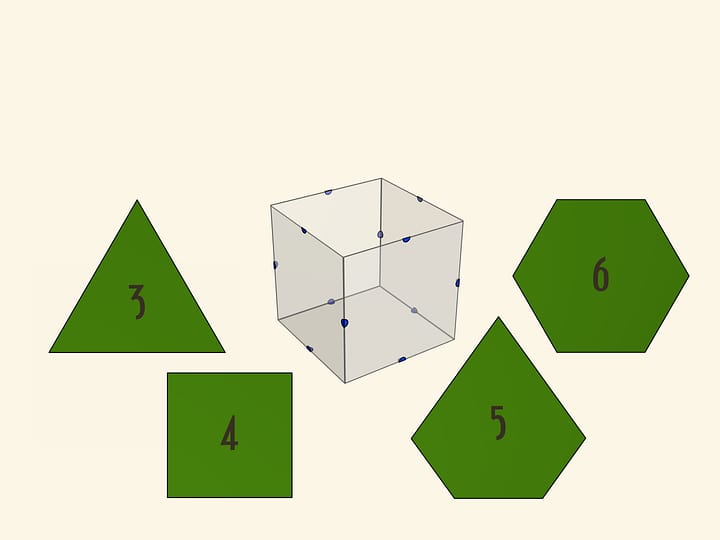
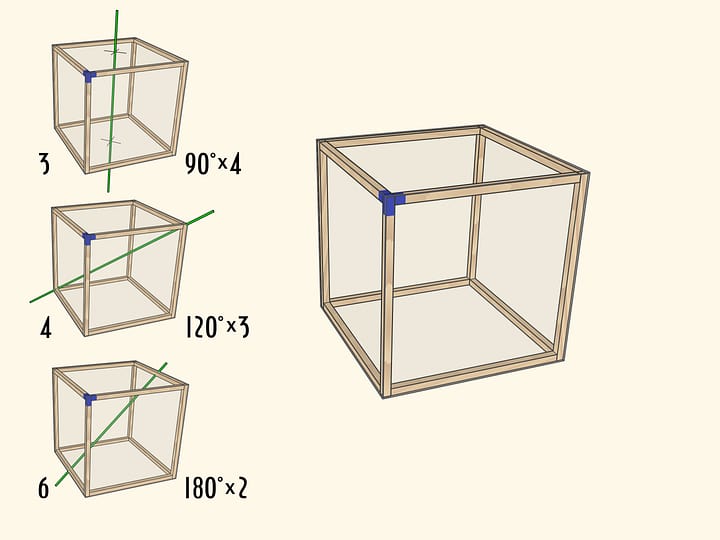
Интересно и полезно увидеть «вживую» и то, как вписывается в куб ещё один правильный многогранник — икосаэдр: «посередине» каждой грани куба будет лежать ребро икосаэдра.
А сколько детей может поместиться в кубический метр? Если провести эксперимент, сделав безопасный куб с ребром в метр и без верхней грани, дети получат удовольствие, а вы — удивитесь результату!
Другие модели раздела «Многогранники»
