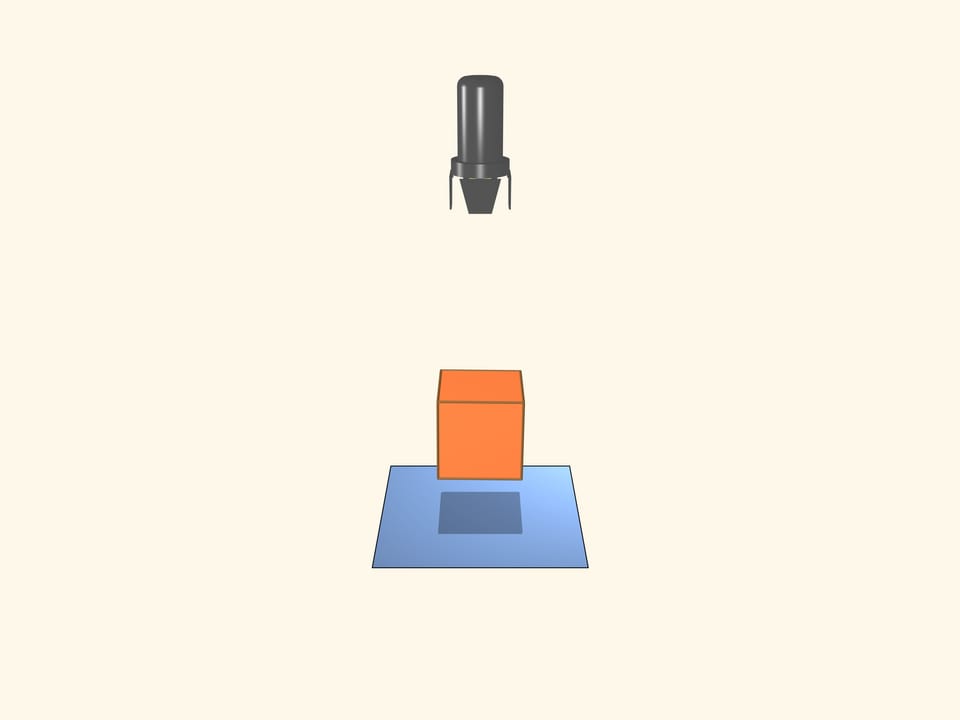
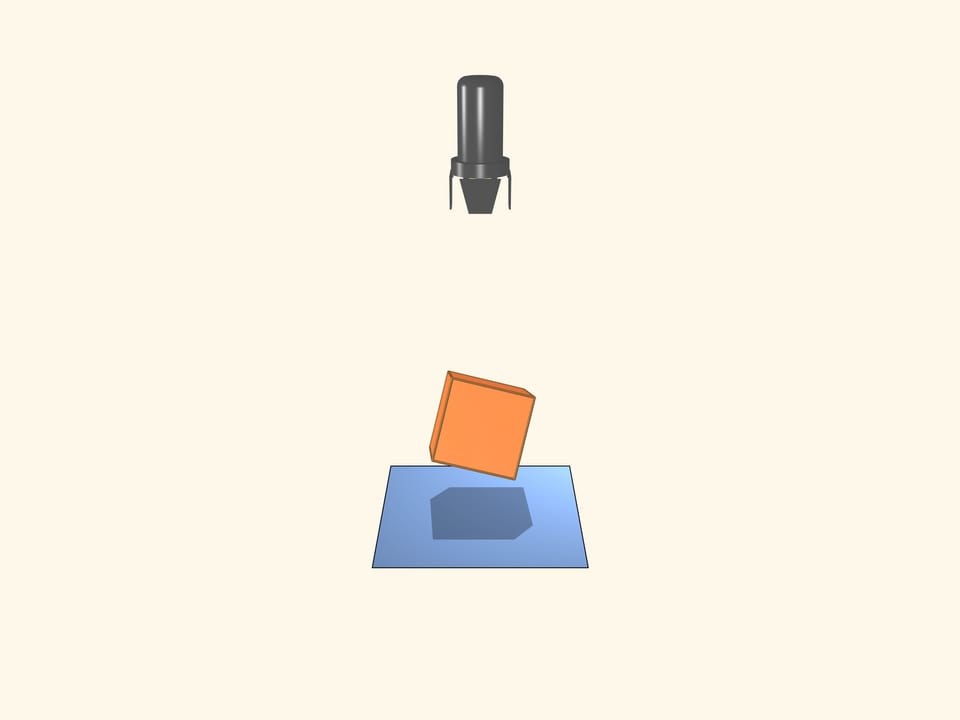
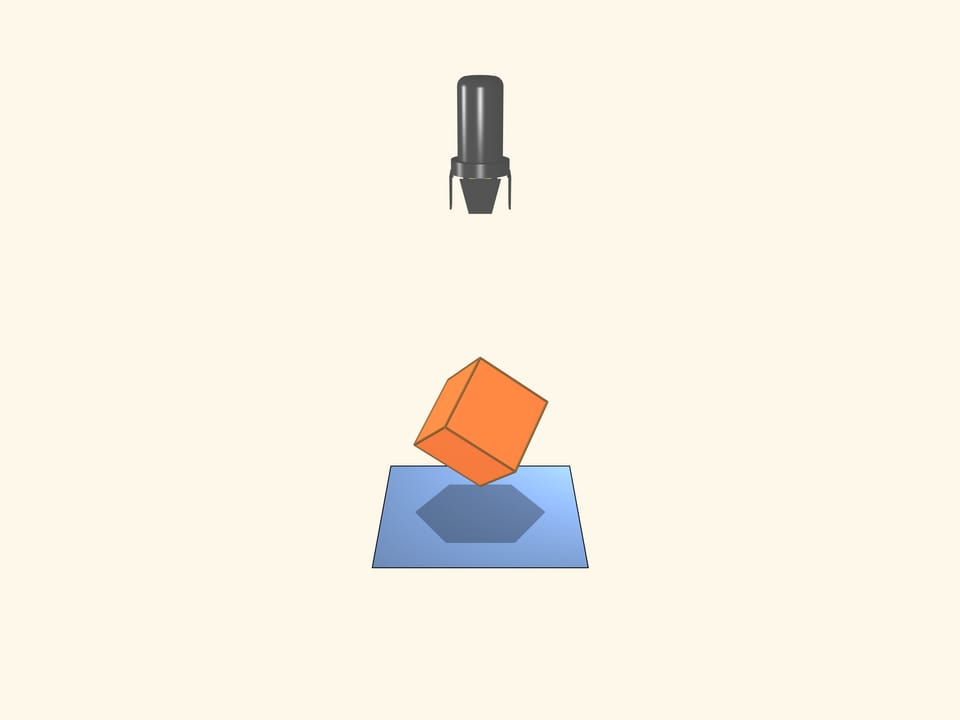
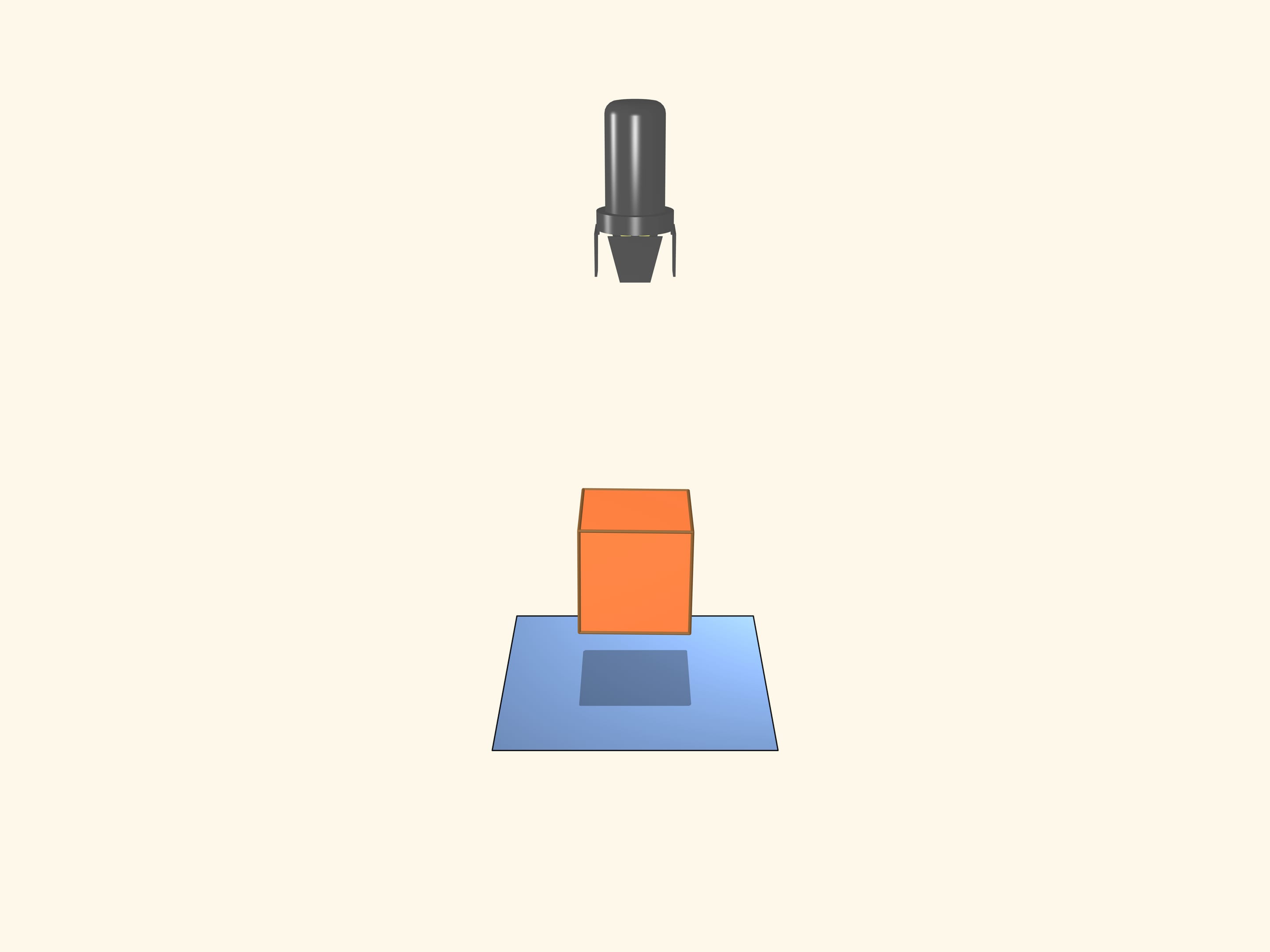
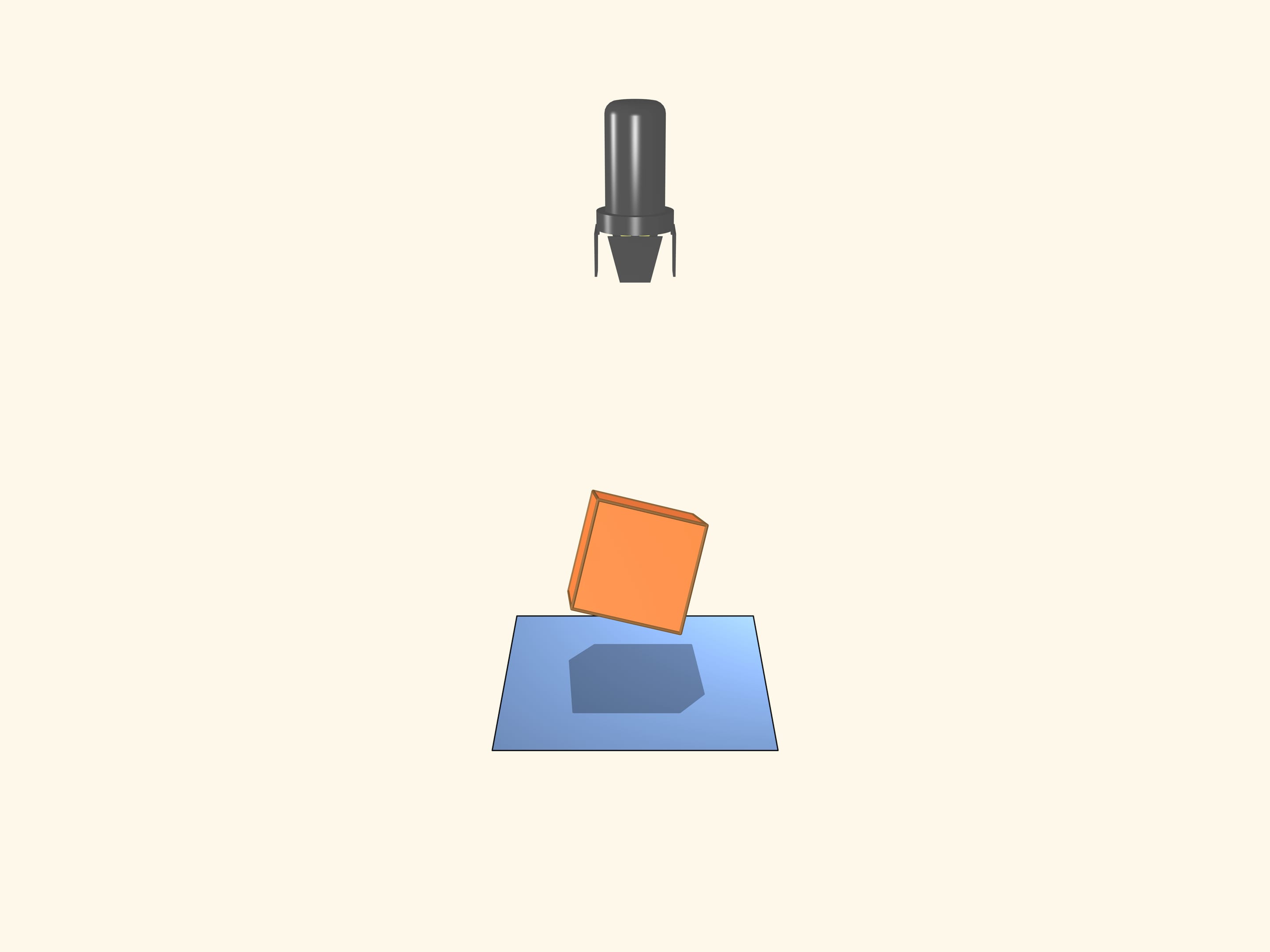
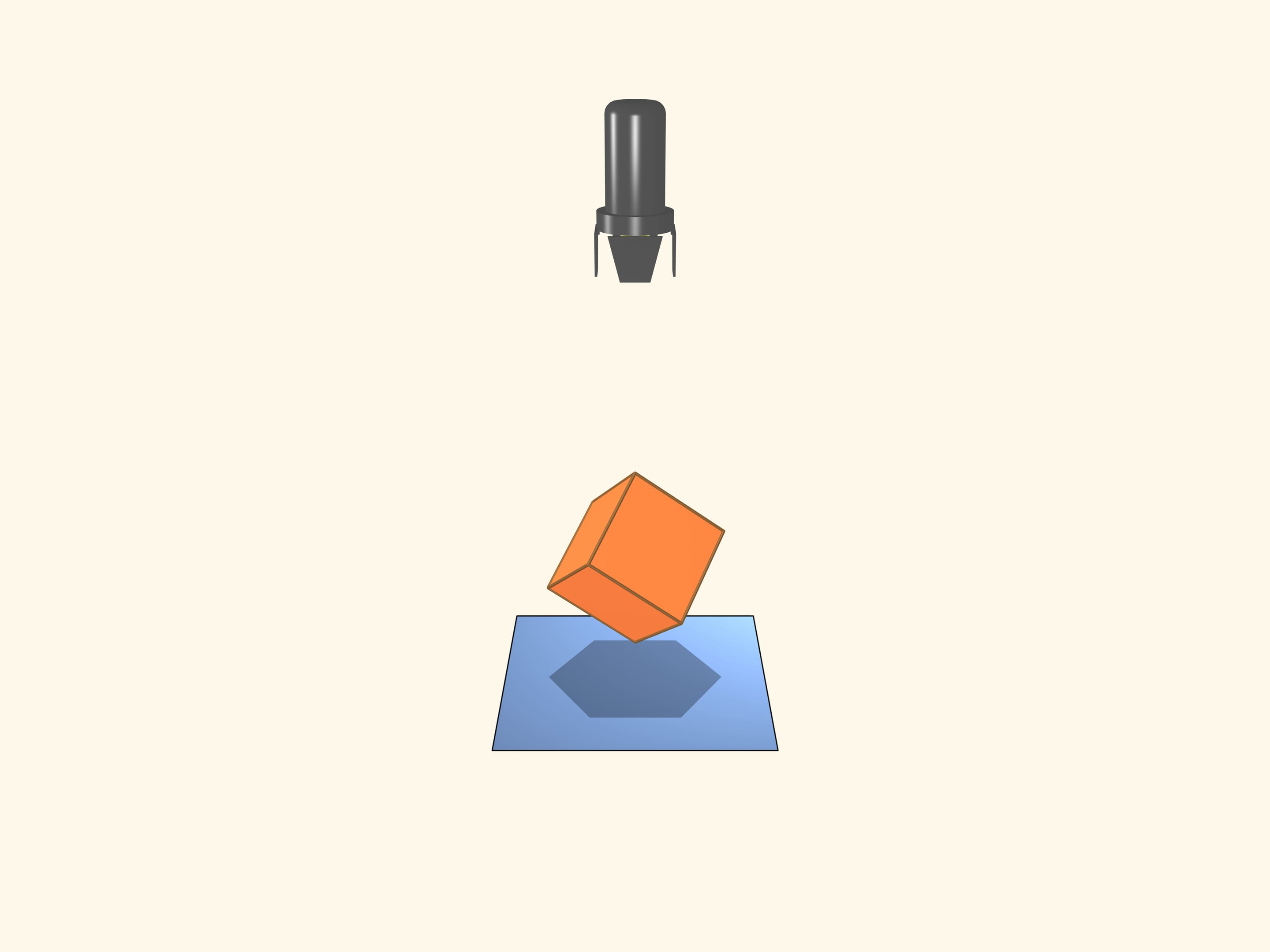
Возьмём прожектор, светящий параллельными лучами. То, что у куба бывает тень в виде квадрата, очевидно. А каково наибольшее число вершин многоугольника, который может являться тенью куба? Если диагональ куба параллельна лучам света, то тенью будет правильный шестиугольник!
Развернём прожектор с экраном и поместим за экран некое тело. Тень на экране-ширме — квадрат. Обязано ли наше тело быть кубом?
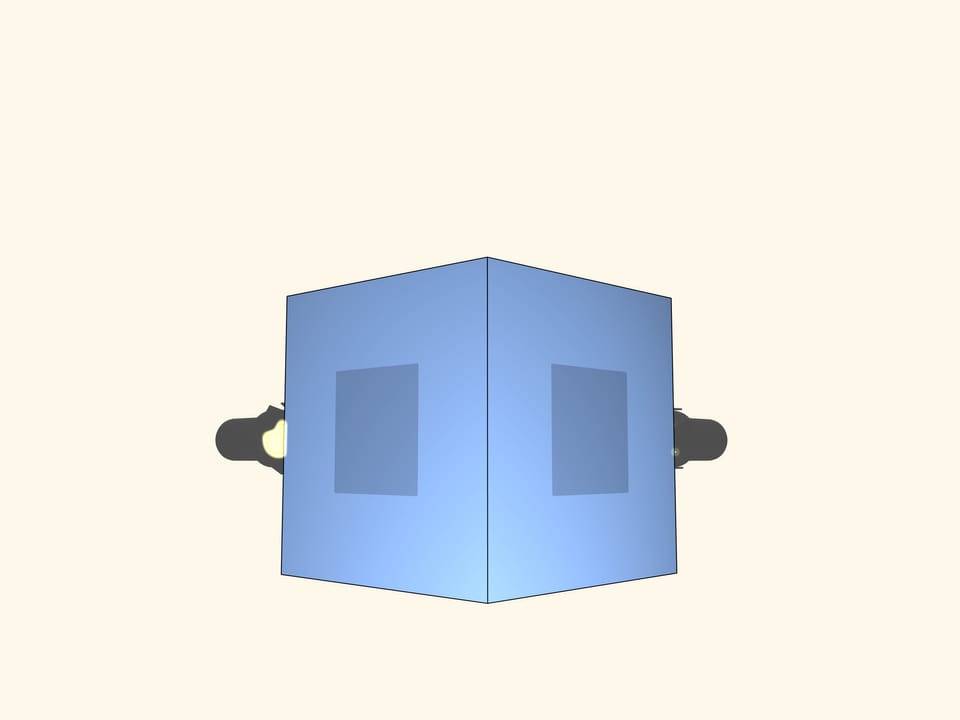
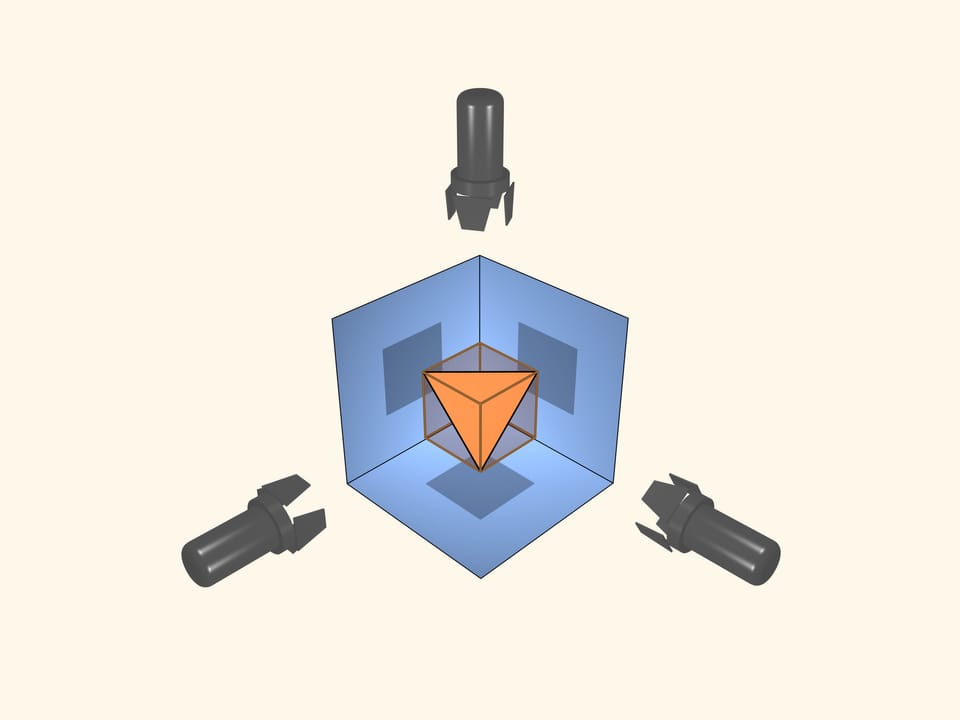
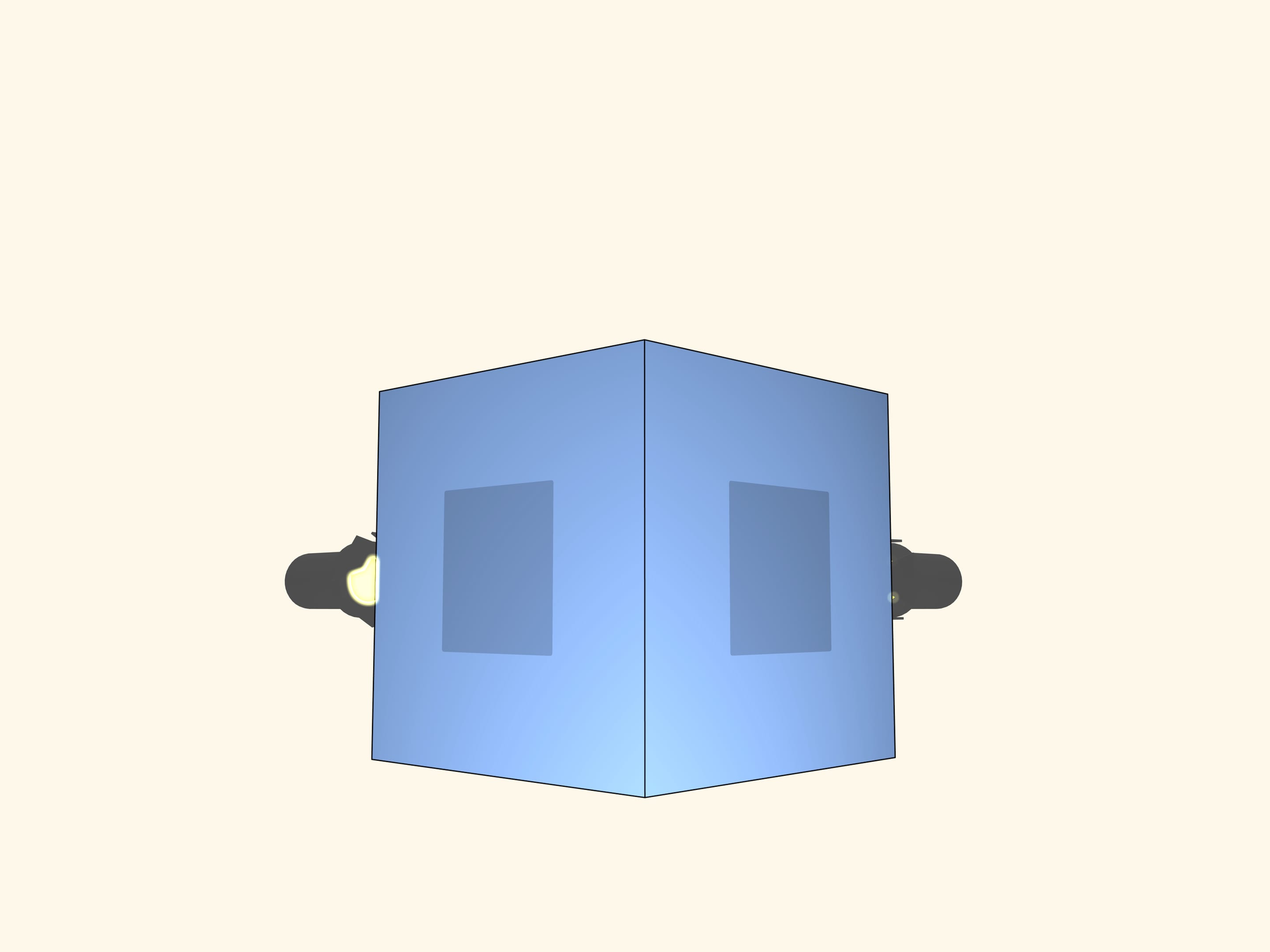
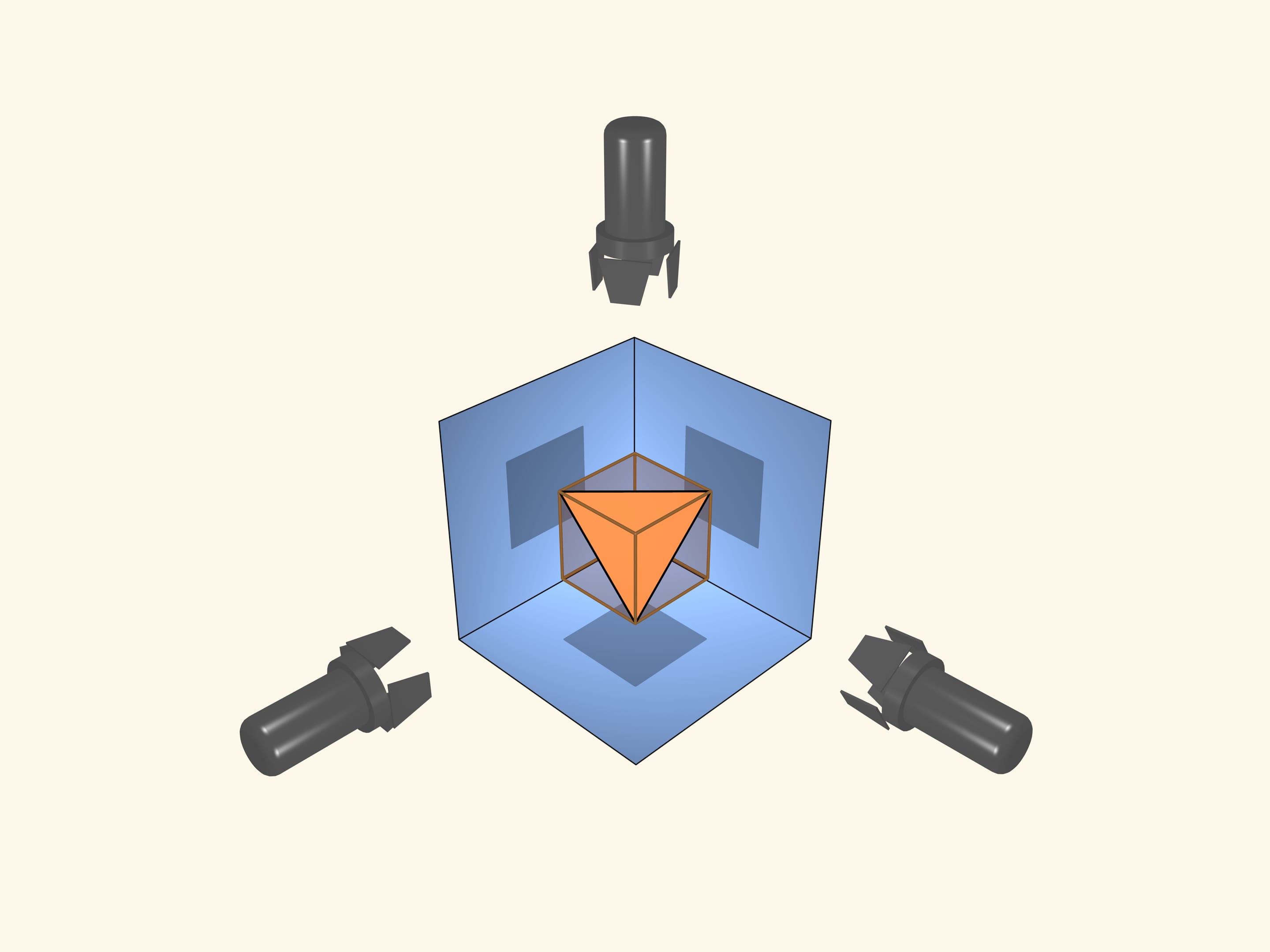
Добавим экран и прожектор в направлении, перпендикулярном первому. Теперь уже две ортогональные (перпендикулярные) проекции — квадраты. Только ли куб может давать такие тени?
А если три ортогональные проекции — квадраты? Бывает ли тело, отличное от куба, имеющее три ортогональные тени в виде квадратов?
Легко придумать невыпуклые тела — например, куб с изъянами — дающие такие проекции. А если при изучении вопроса ограничиться рассмотрением только выпуклых тел, или даже ещё более узкого класса — правильных многогранников?
Оказывается, что бывает даже правильный многогранник, отличный от куба, дающий тени в виде квадратов в трёх перпендикулярных направлениях.
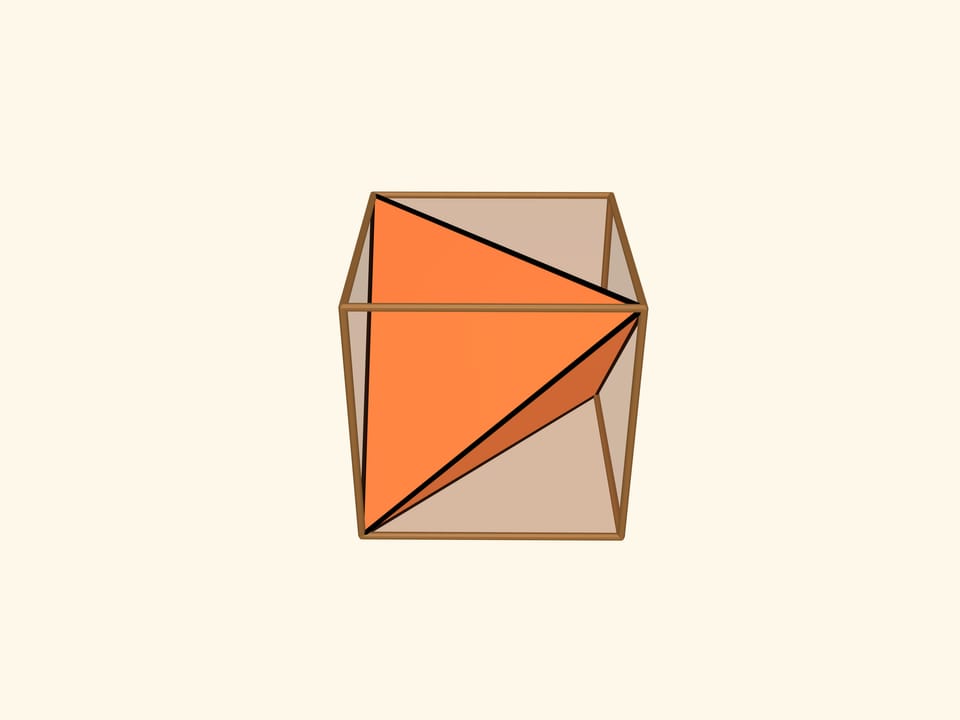
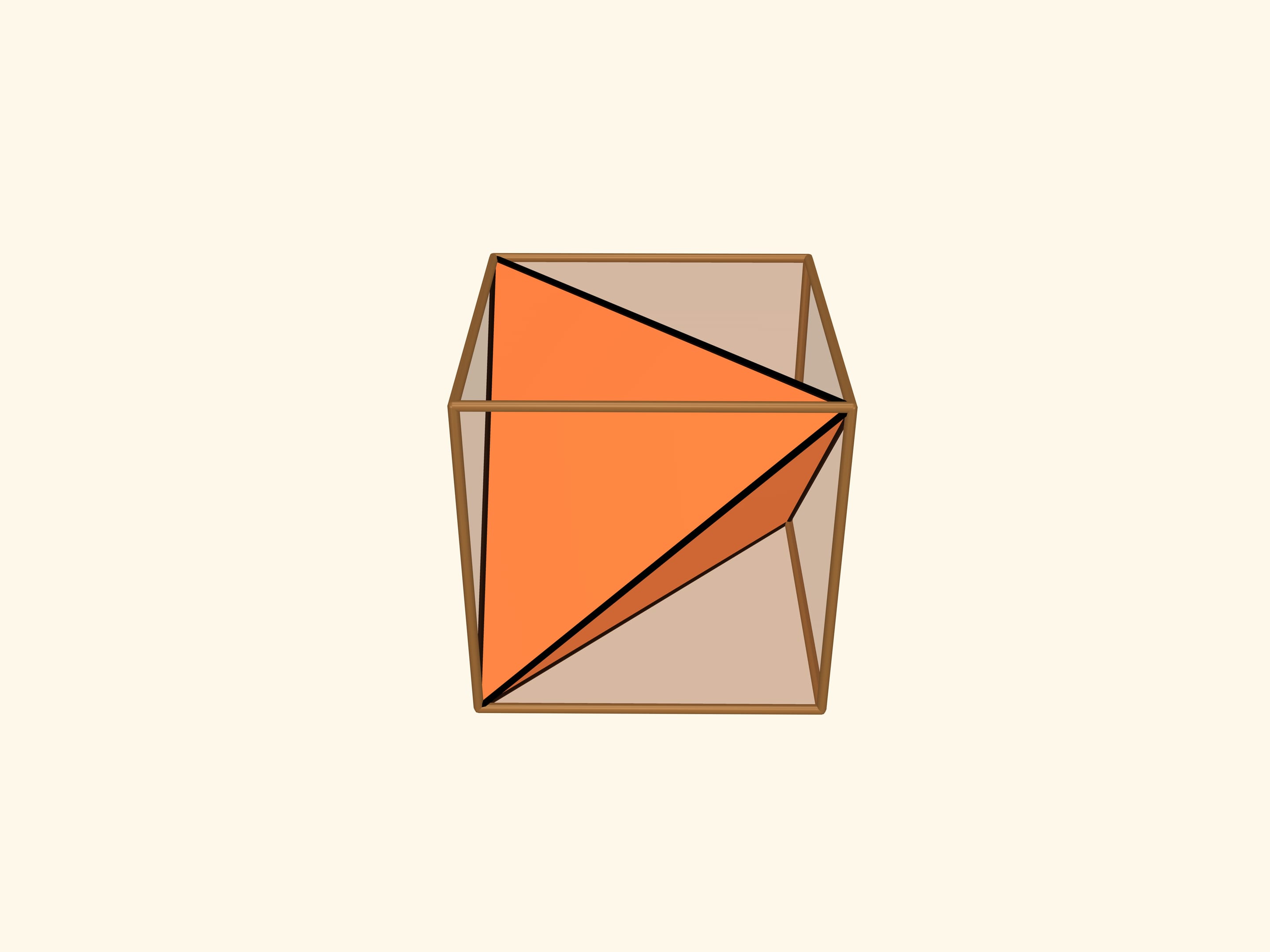
Действительно, в куб можно вписать правильный тетраэдр! Четыре вершины тетраэдра будут совпадать с вершинами куба. Все рёбра тетраэдра будут являться диагоналями граней куба и, следовательно, будут равны между собой.
Если посмотреть через какую-либо грань куба, то так расположенный правильный тетраэдр «занимает» всю проекцию куба вдоль направления, перпендикулярного грани.
Значит, если куб расположен так, что три его ортогональные проекции — квадраты, т. е. экраны параллельны граням куба, то и правильный тетраэдр, вписанный в него, будет давать те же самые тени — три квадрата.