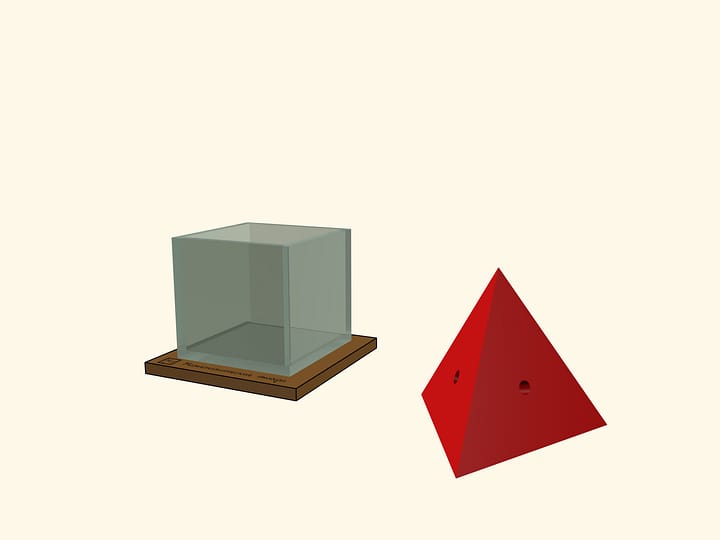
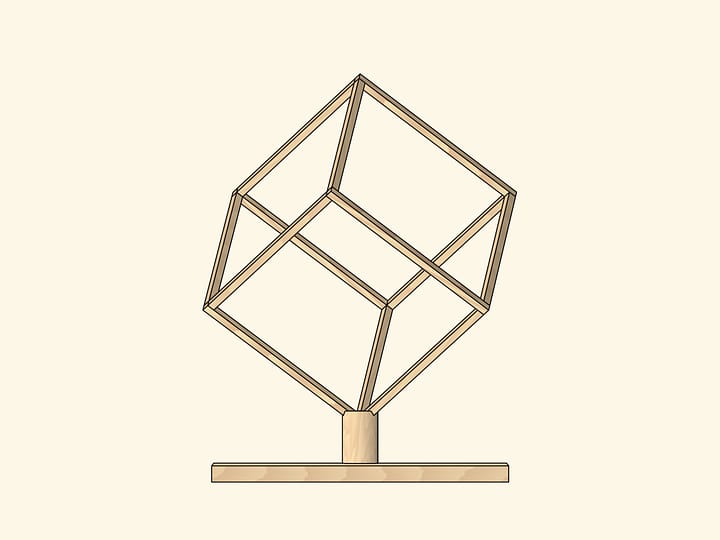
Основой модели является прозрачный пластиковый куб без верхней грани. Он может быть собран из развёртки, сделанной из пластика, держащего углы после сборки.
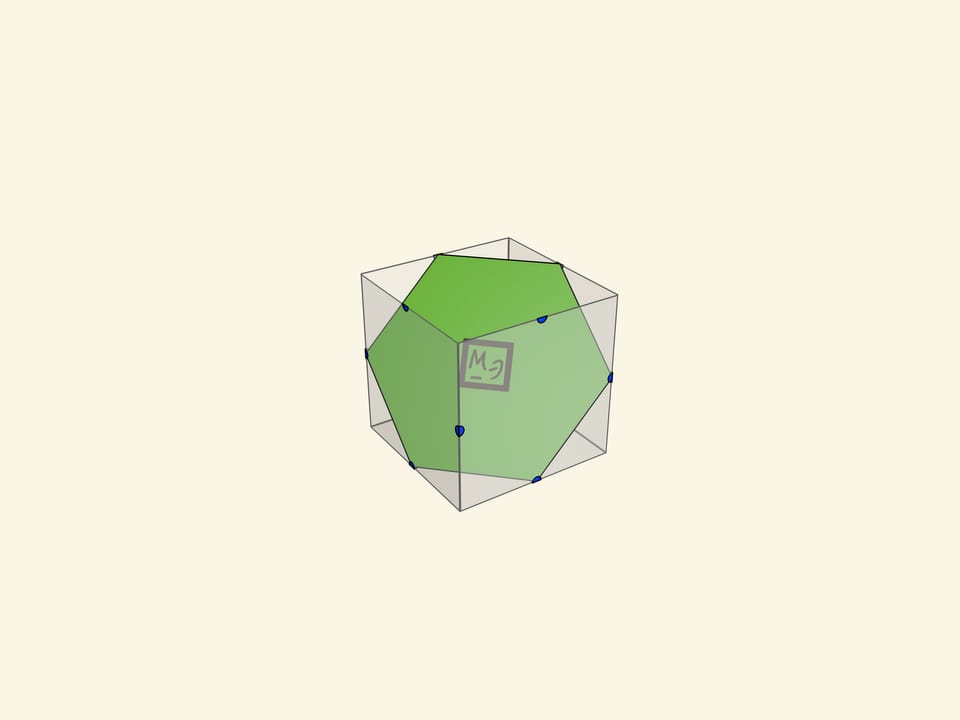
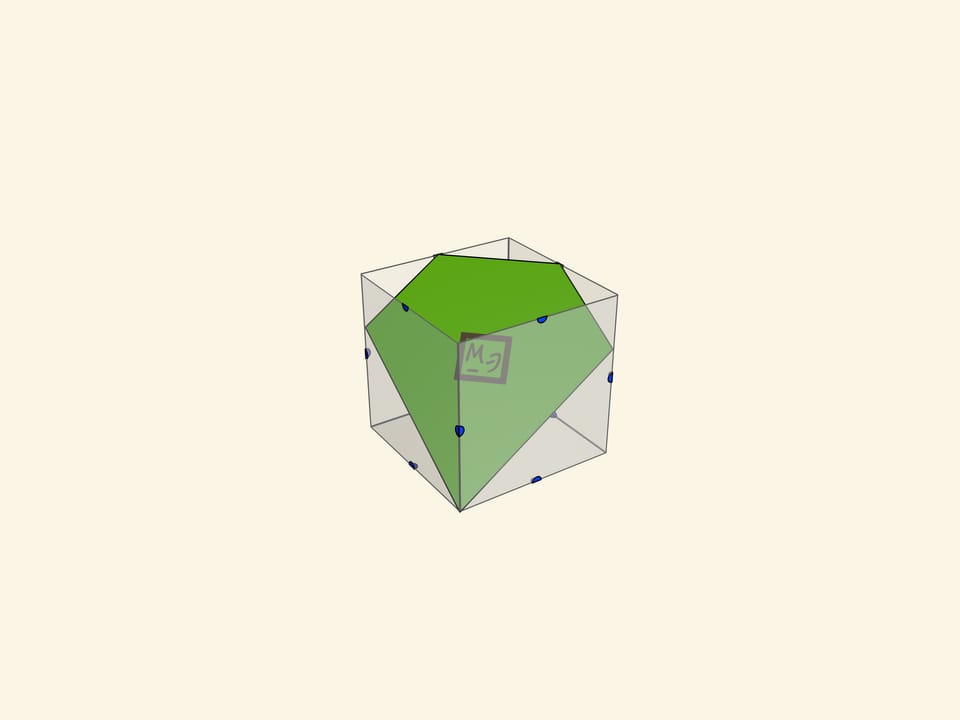
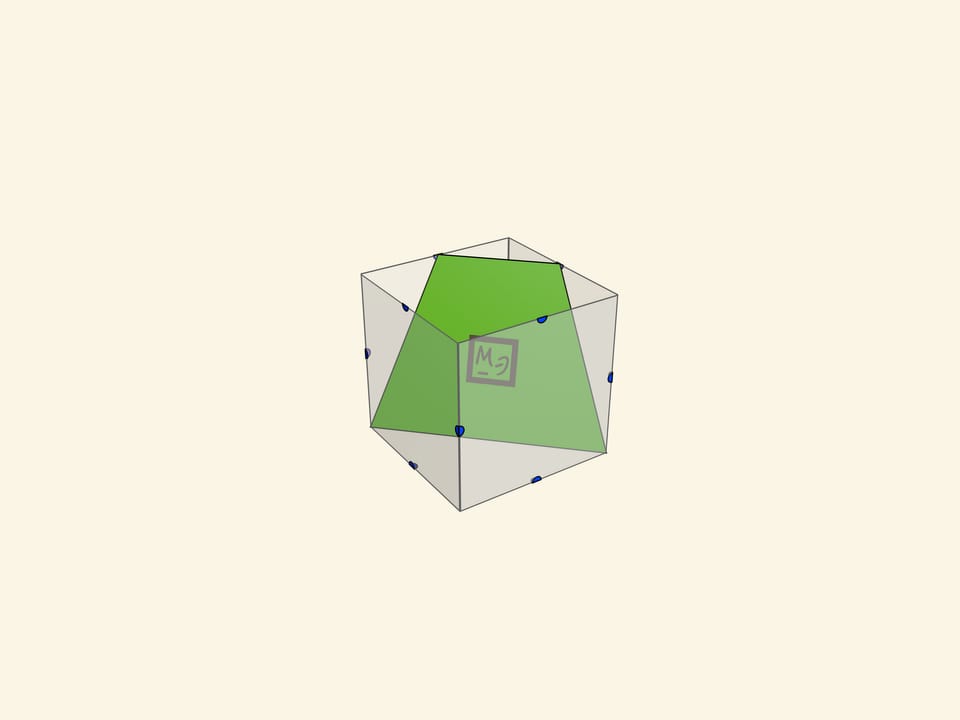
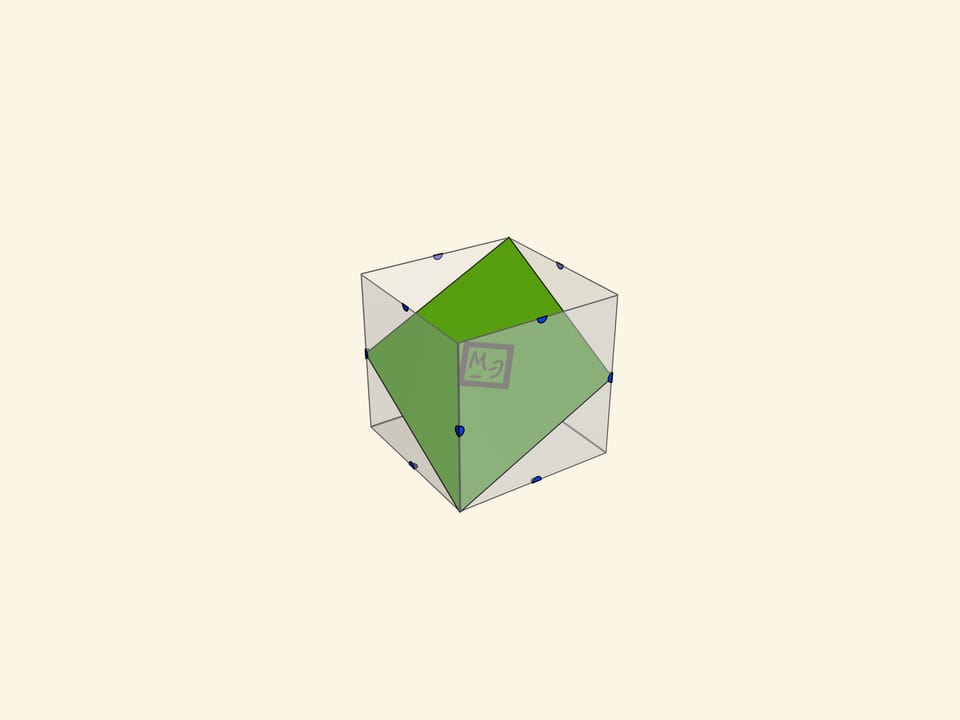
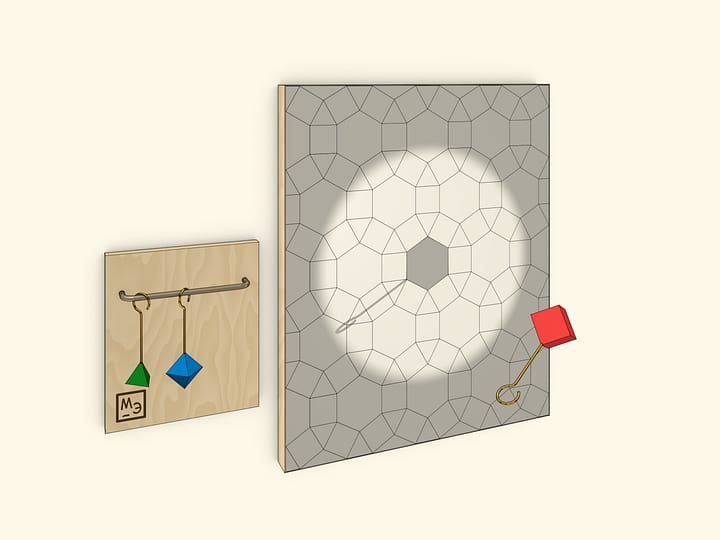
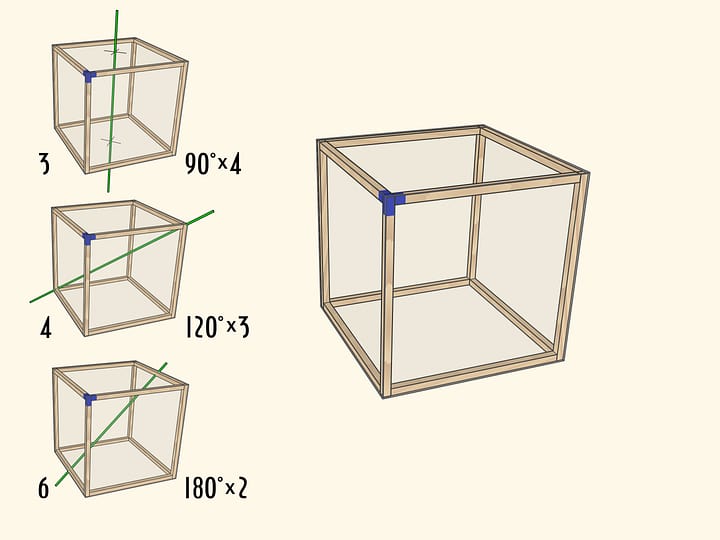
Сечения куба можно вырезать из плотного, но тонкого картона. Стоит сделать все типы сечений куба:
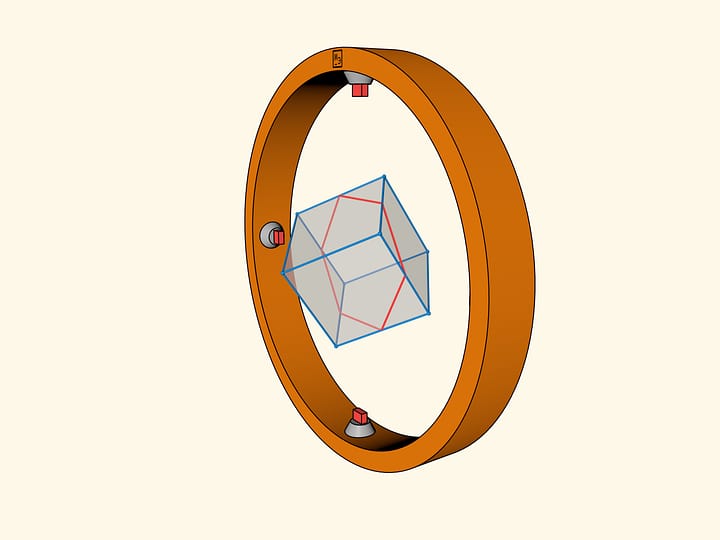
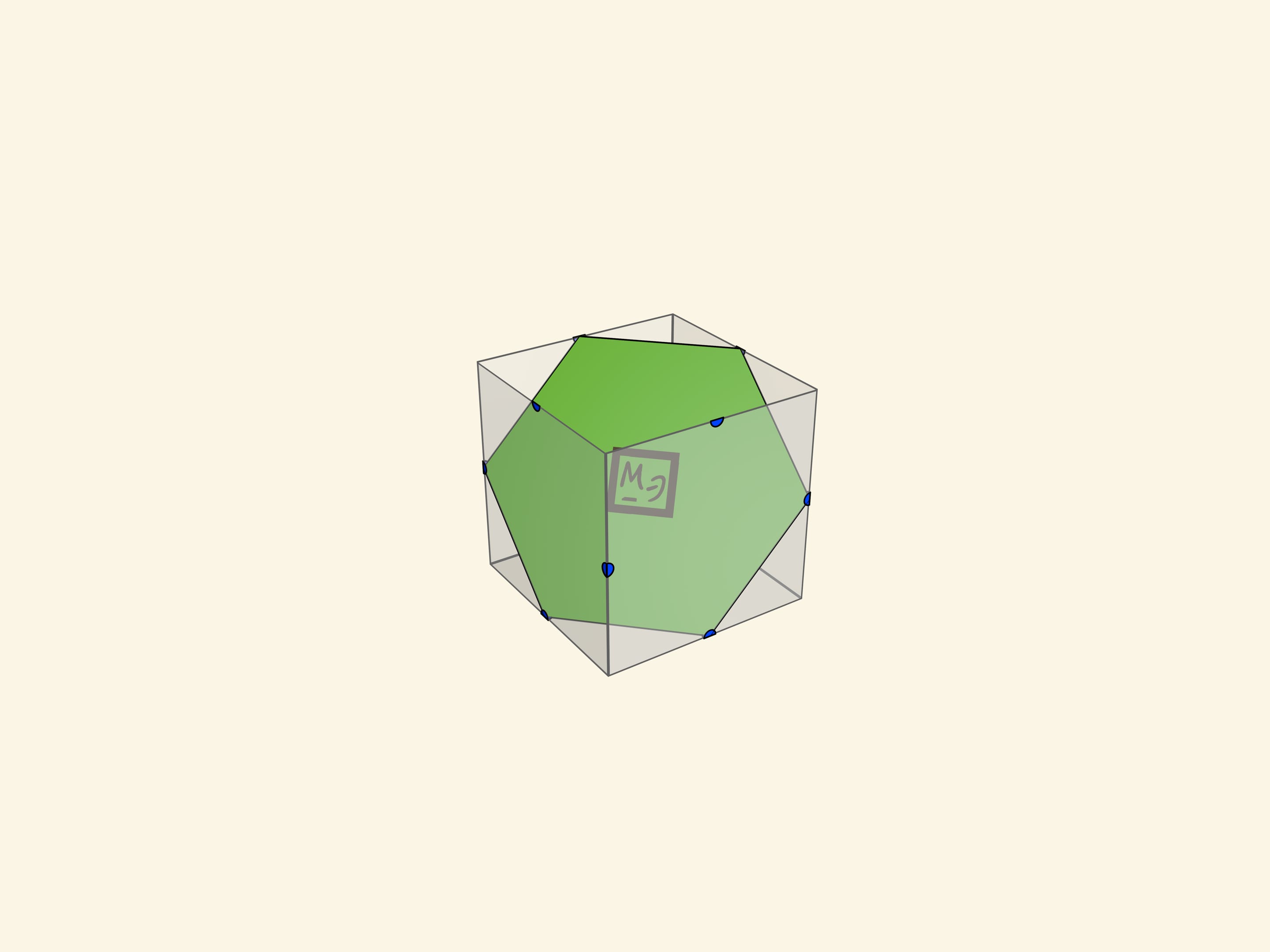
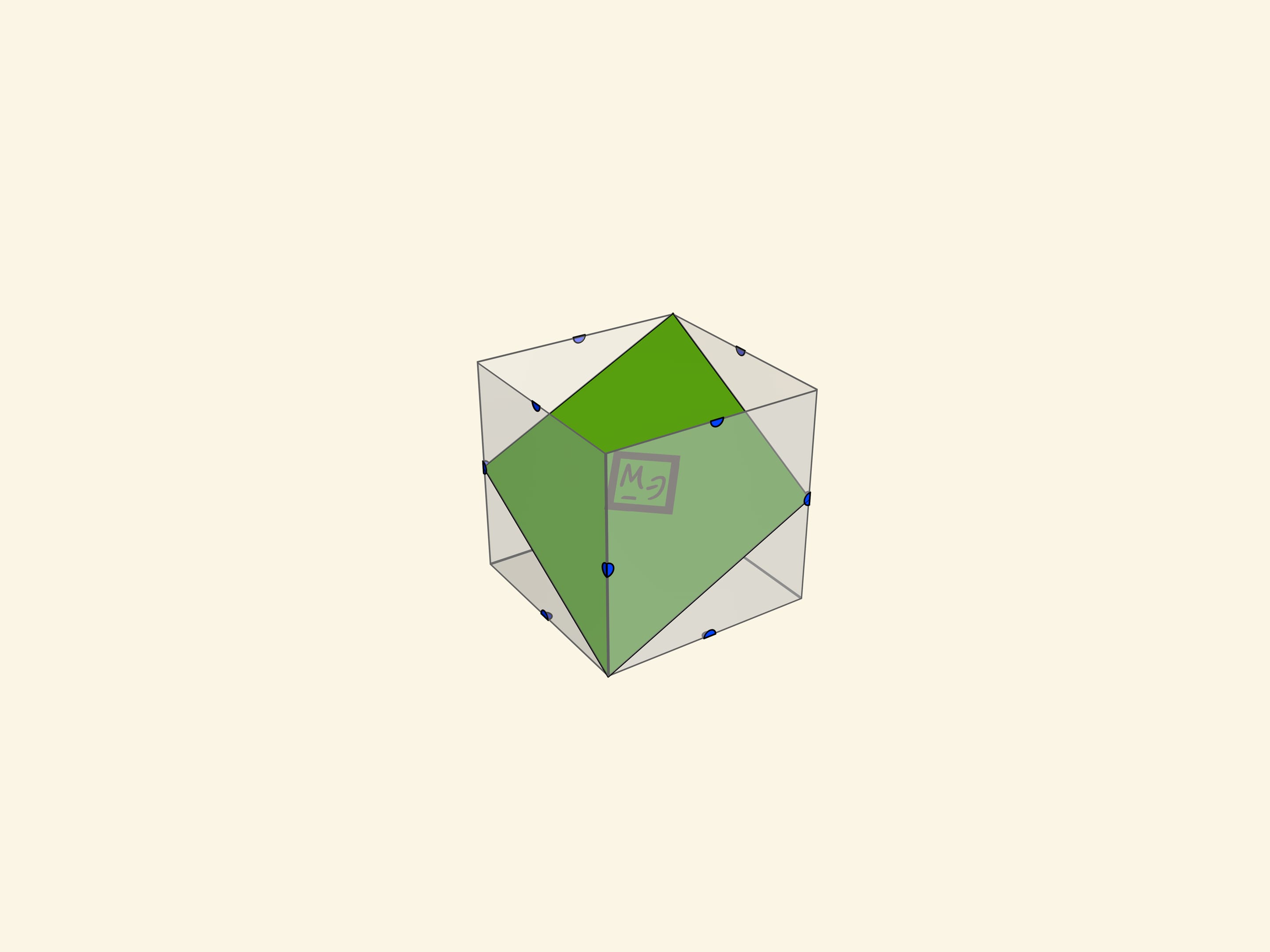
- правильный шестиугольник;
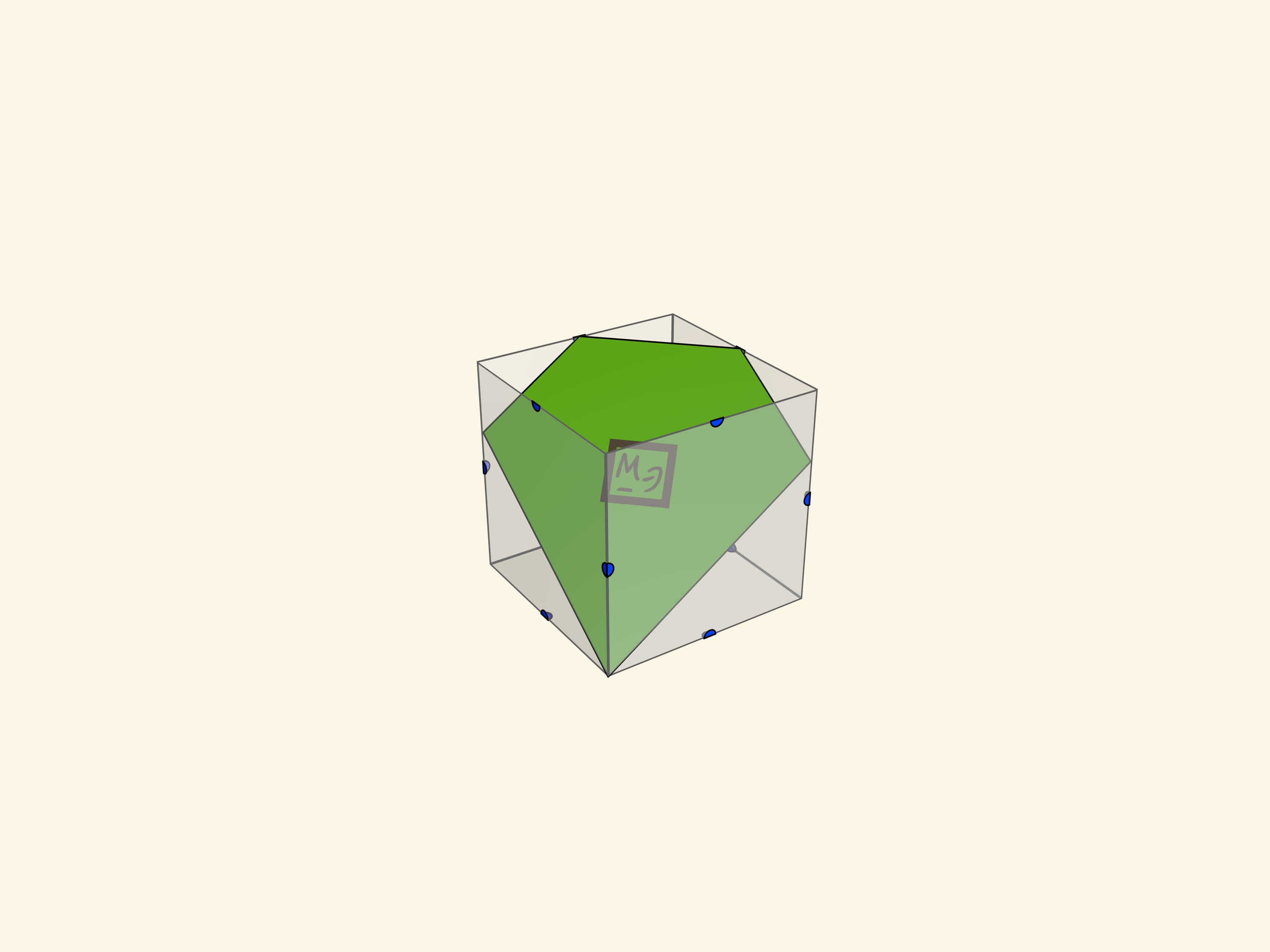
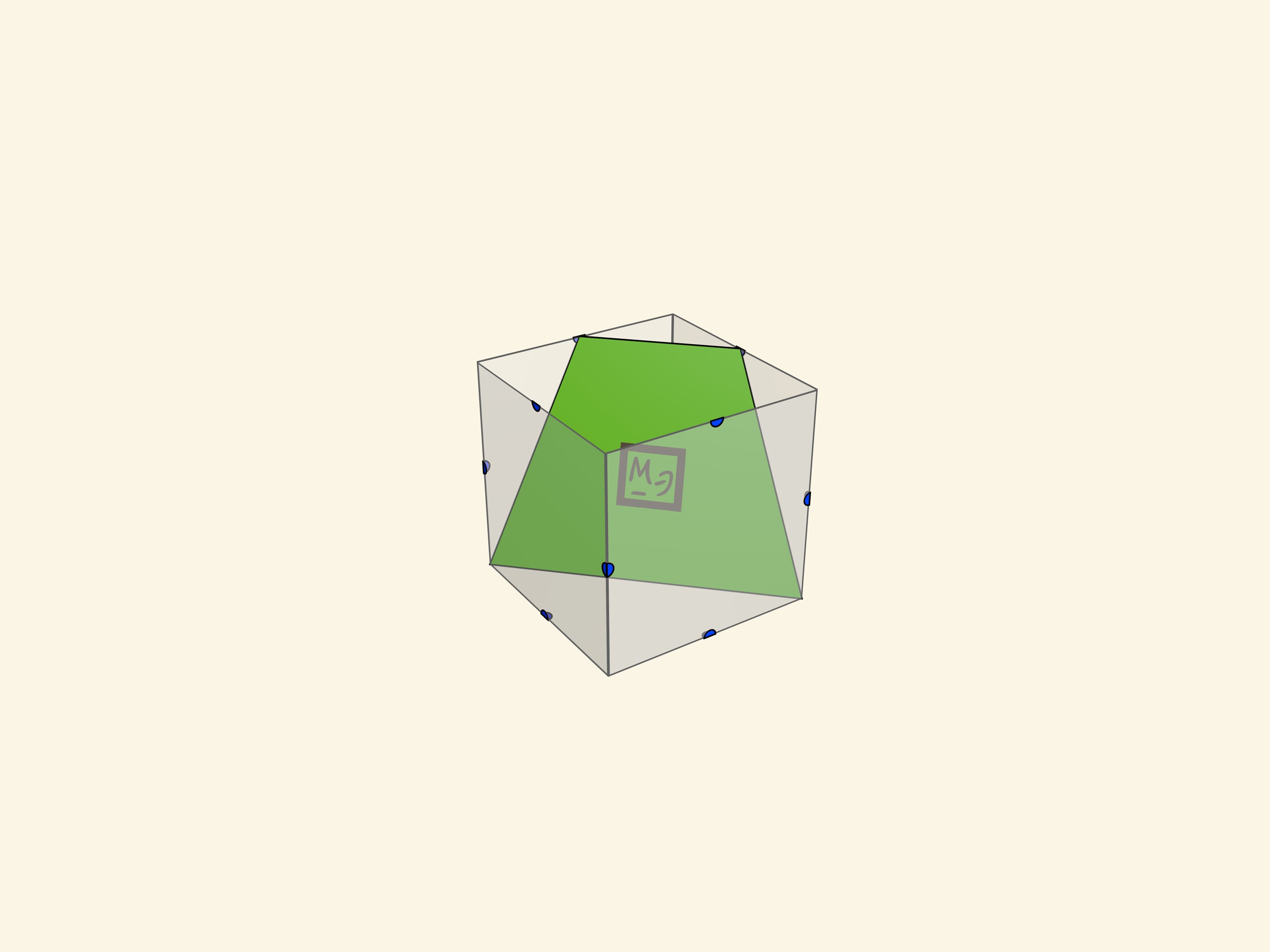
- пятиугольник (неправильный);
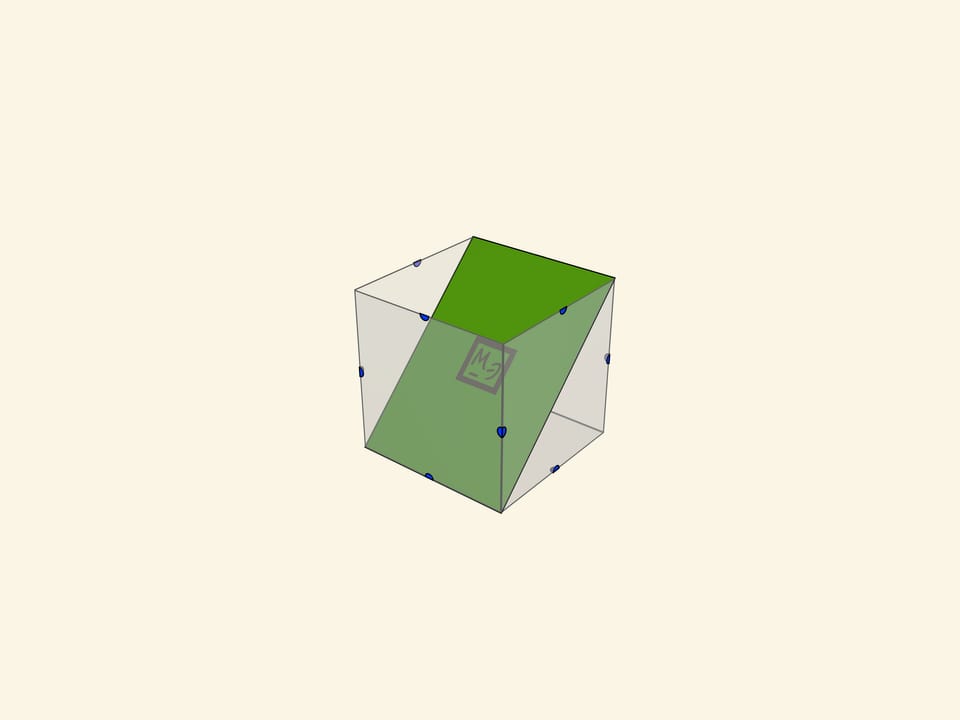
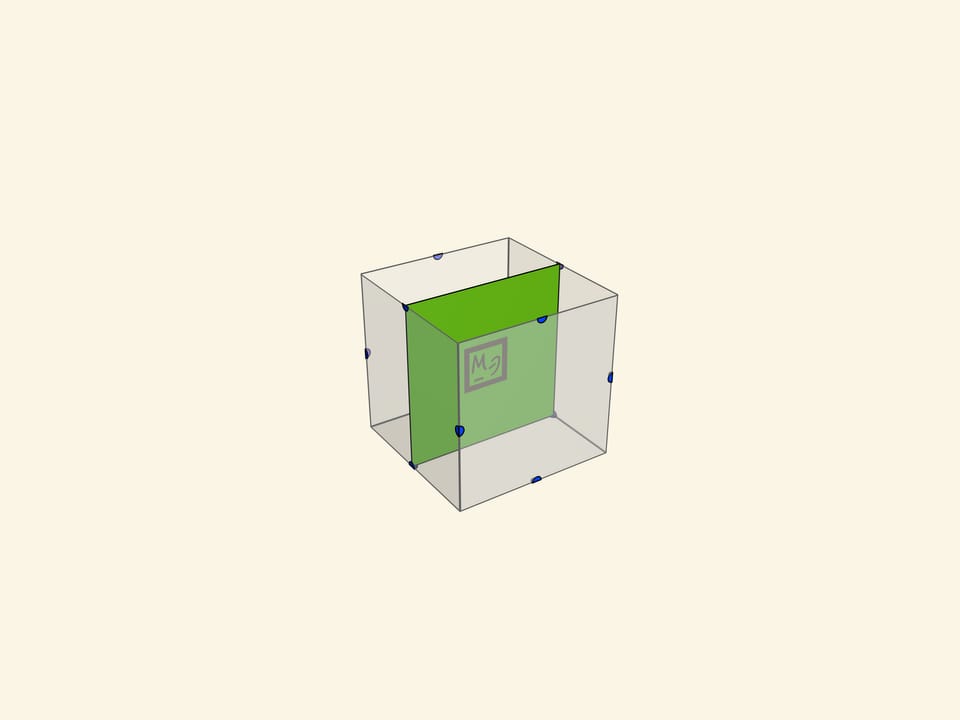
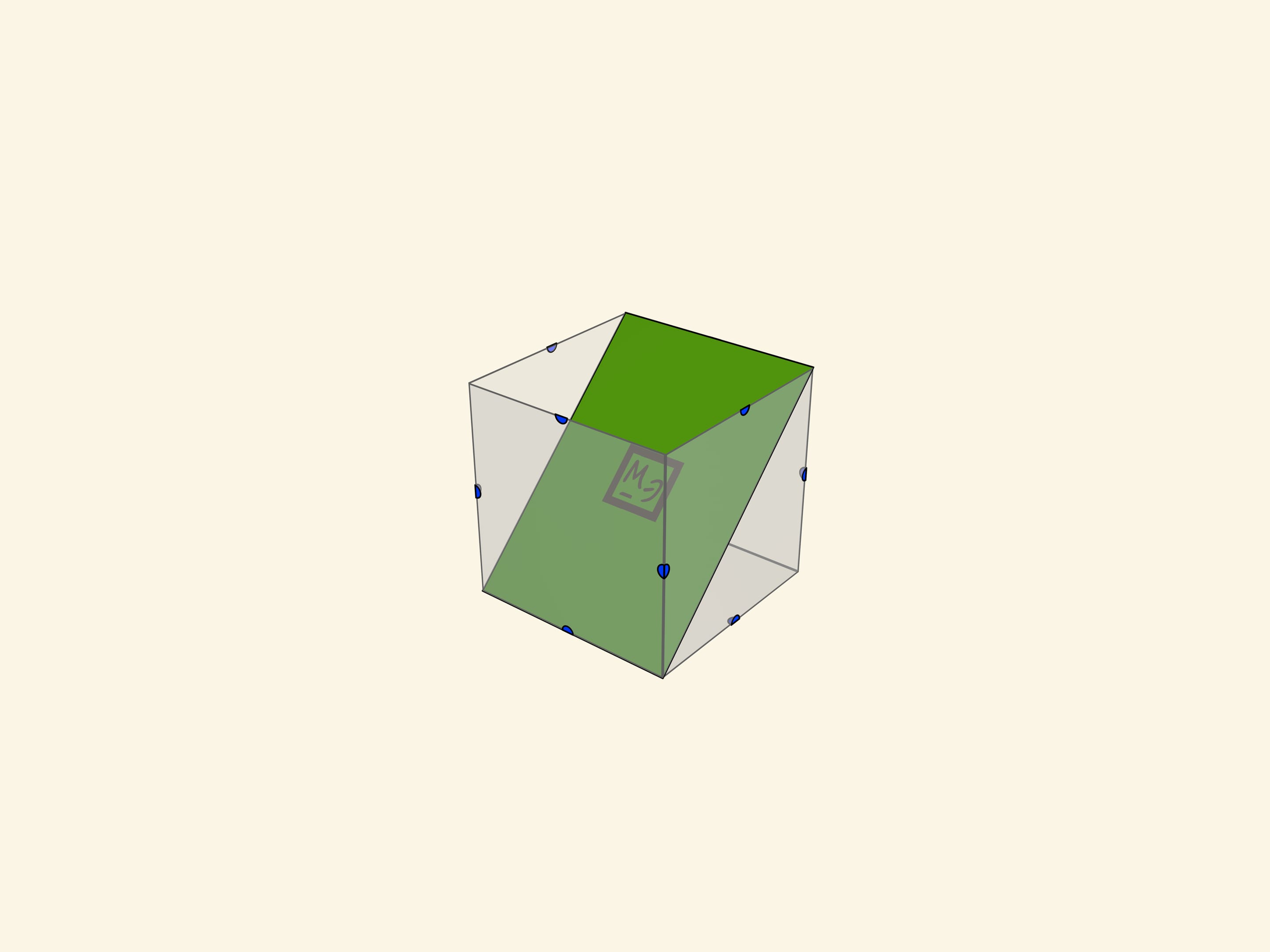
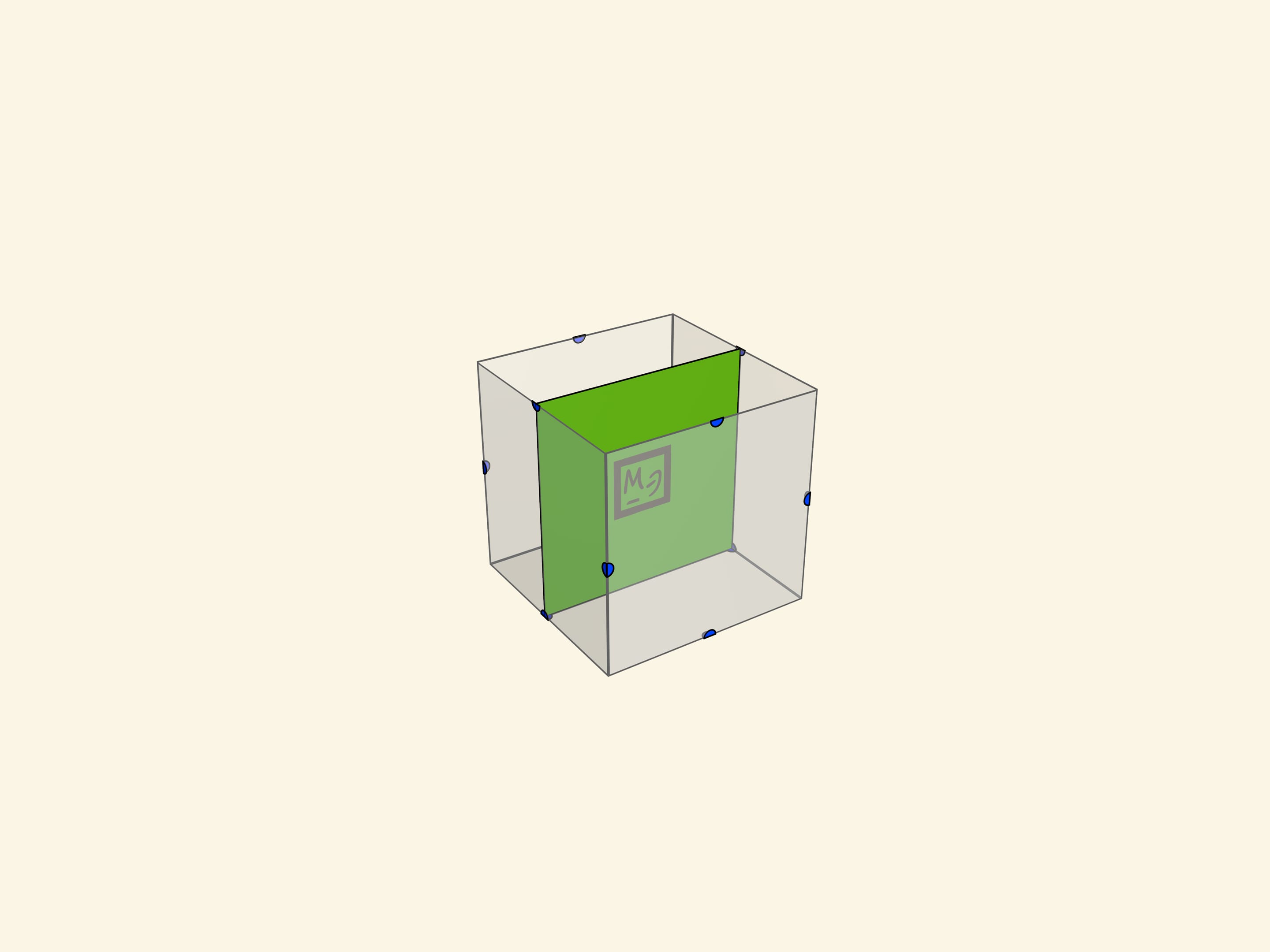
- различные четырёхугольники (включая квадрат, прямоугольник, ромб);
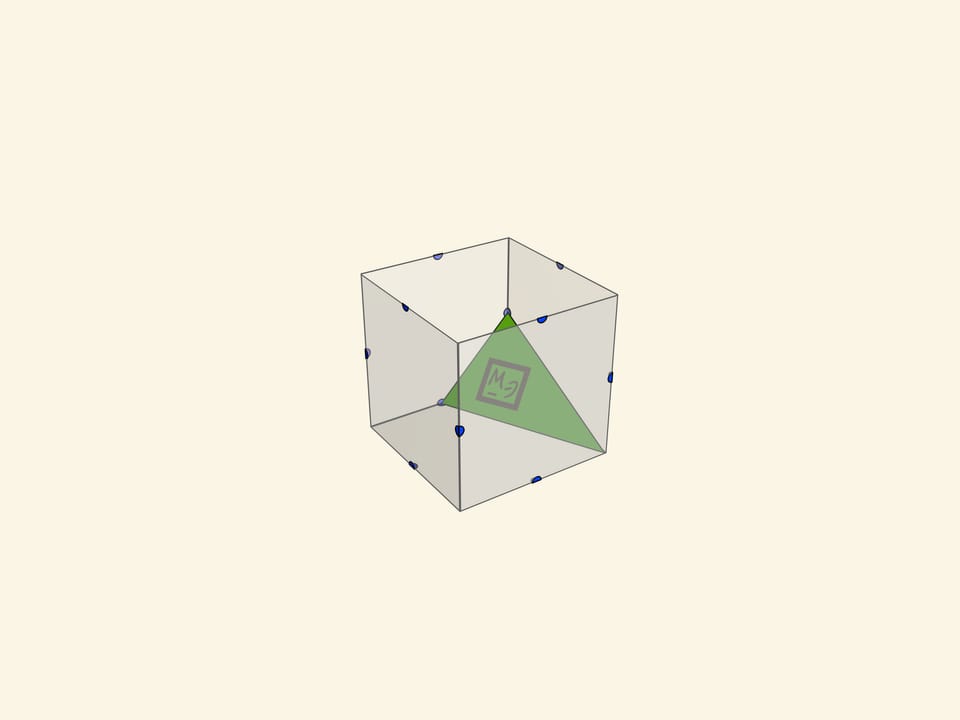
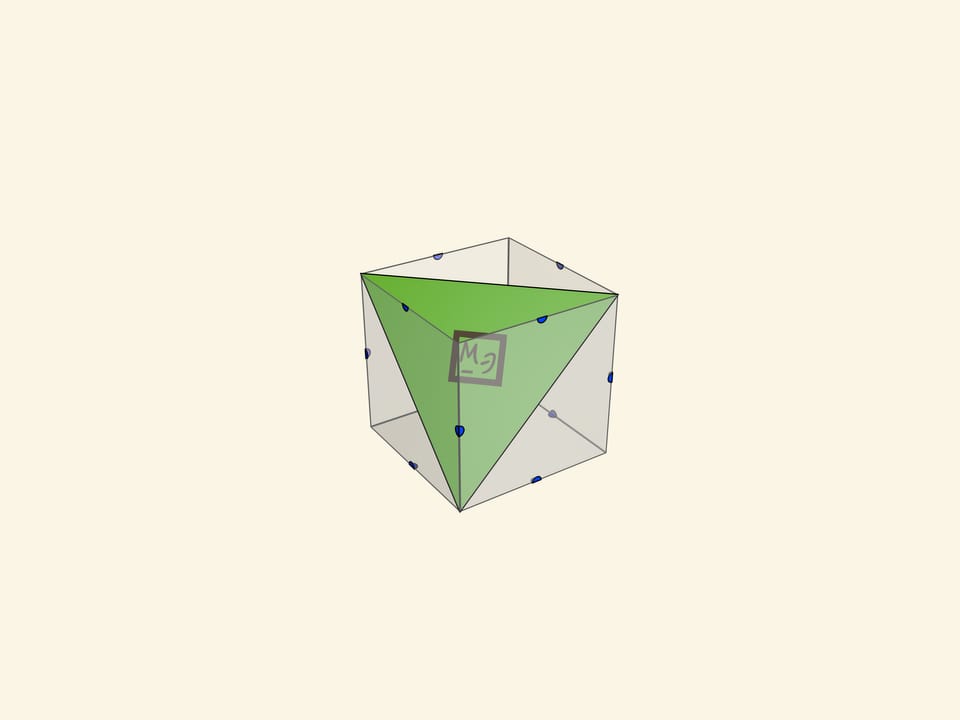
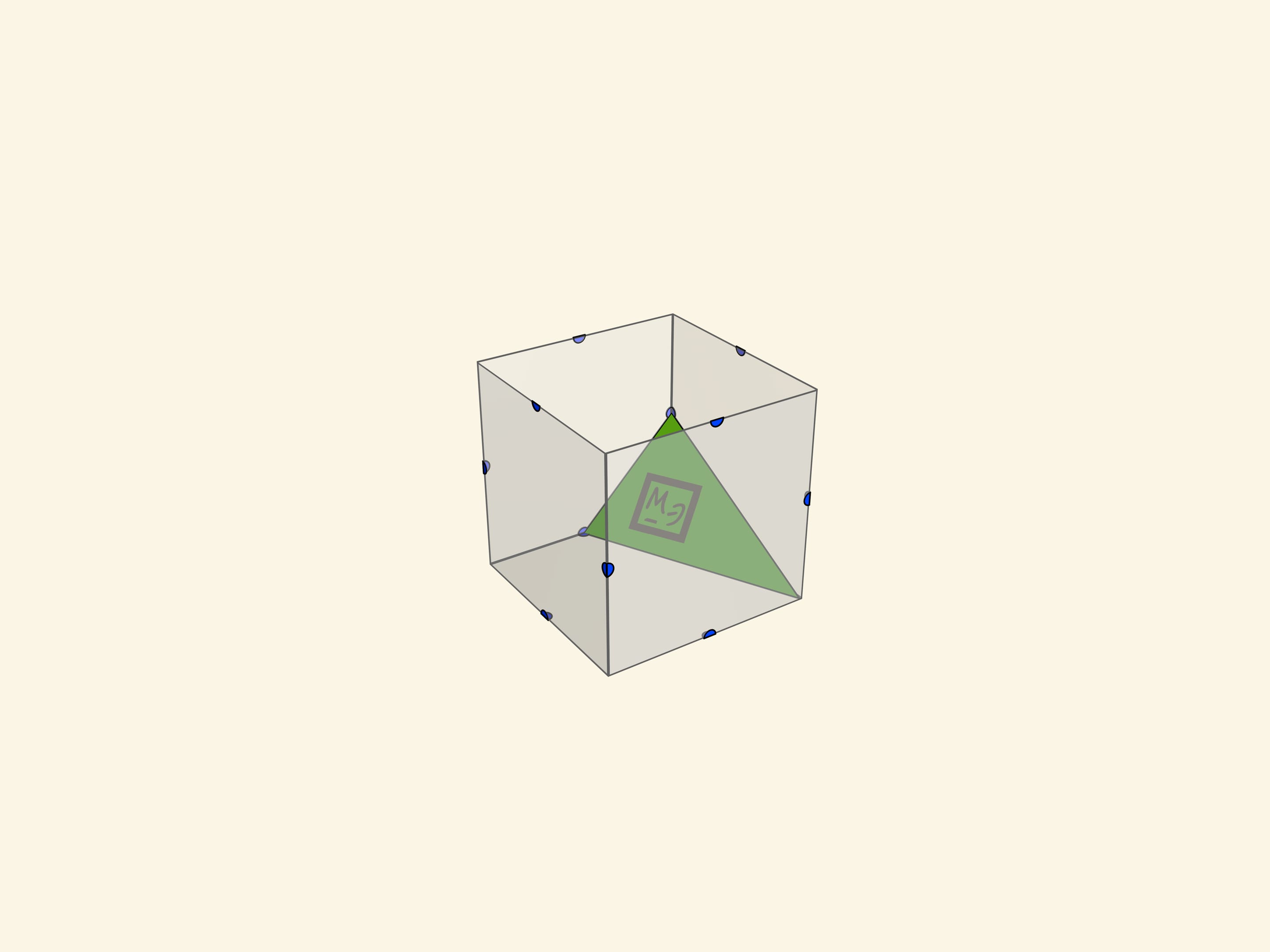
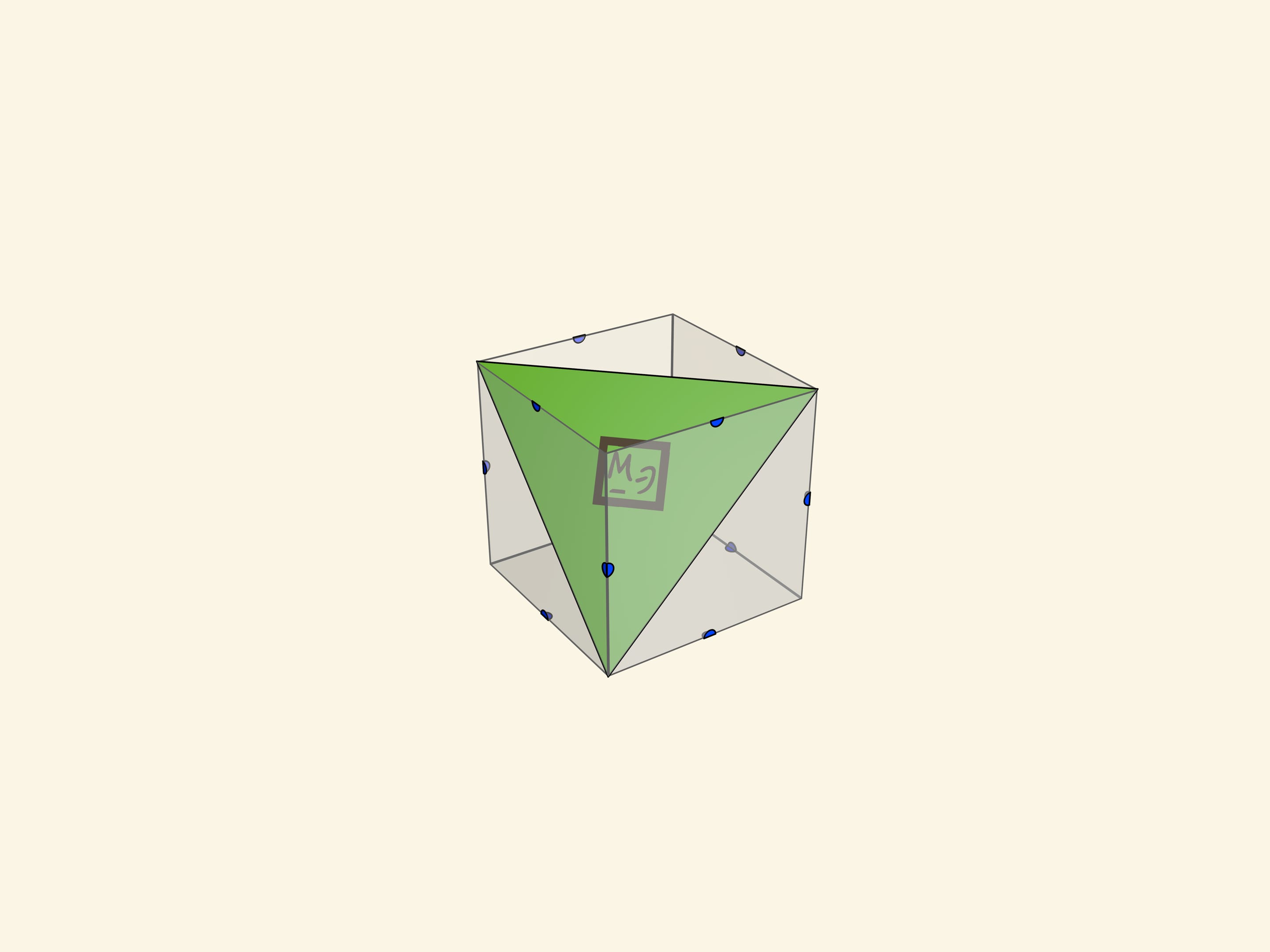
- а также различные треугольники (включая правильный).
Учащимся предлагается разместить (как сечение) каждый многоугольник в кубе.
Можно предложить и самим учащимся вырезать многоугольник, являющийся сечением куба.
Интересно обсудить, почему у куба не бывает сечения в виде пятиугольника правильного. Плоскость, высекающая пятиугольник, пересекается с пятью гранями куба, а значит, среди них будут две параллельные грани (а на самом деле — две пары). Пересекаясь с одной плоскостью, они дадут параллельные отрезки, а у правильного пятиугольника нет параллельных сторон.
Такой же вопрос — какие правильные многоугольники можно получить как сечение — интересно рассмотреть и для других правильных многогранников, начиная с тетраэдра и заканчивая додекаэдром.
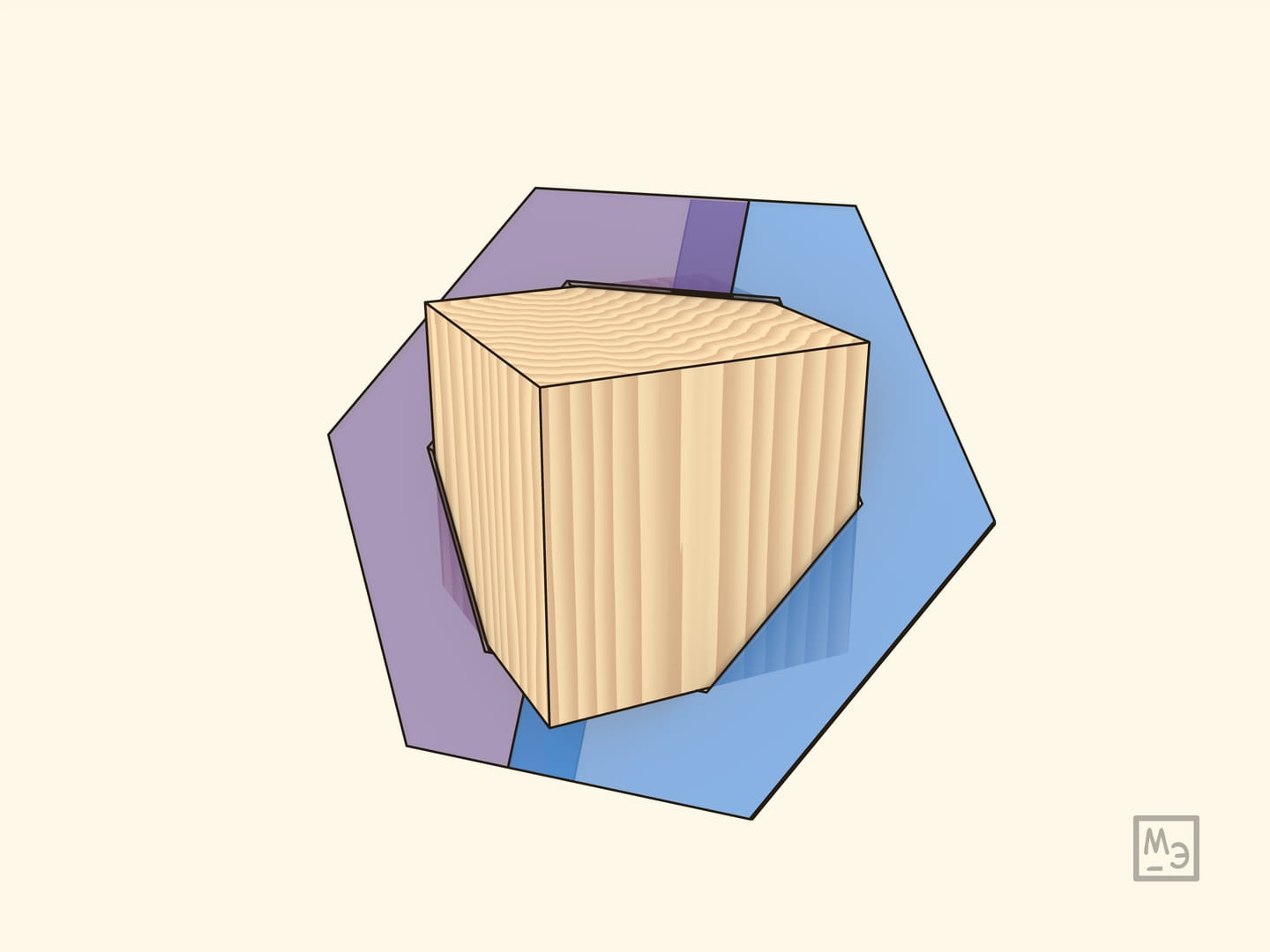
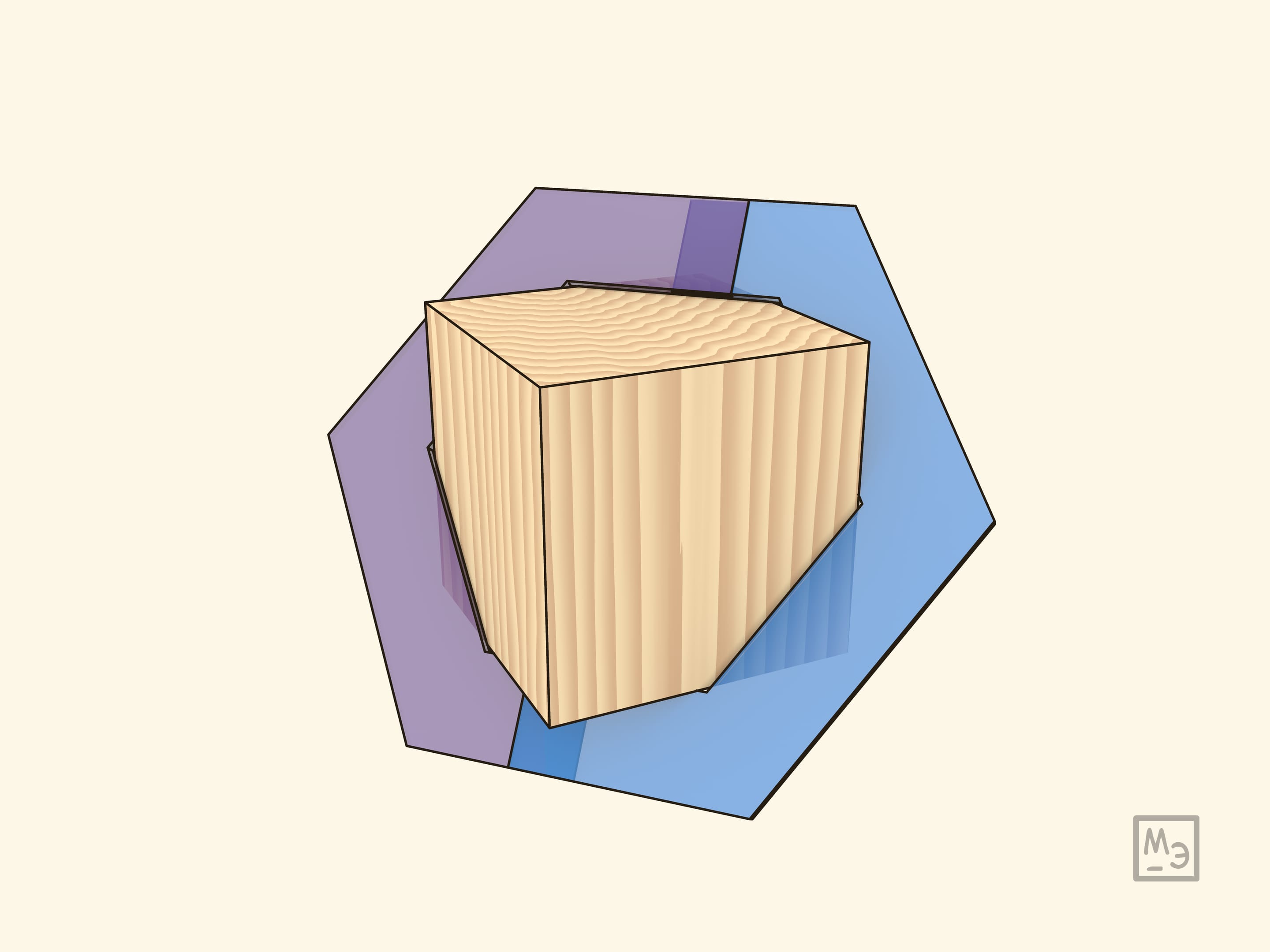
Модель, демонстрирующую сечение куба в виде правильного шестиугольника, можно сделать в виде «воротника» на куб.
Воротник необходимо делать из двух частей, так как снять его целиком – невозможно (что тоже полезно обсудить с учащимися).