Оси вращения куба ⁠

Какие пово­роты пере­во­дят куб в себя, и сколько их? Какими осями опре­де­ляются эти пово­роты?

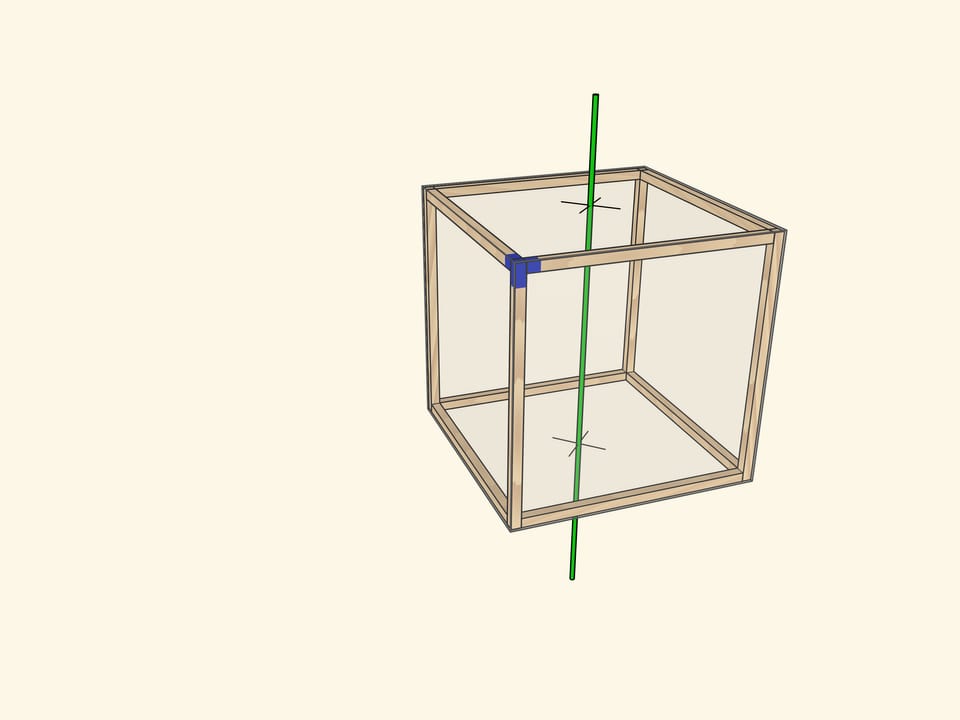
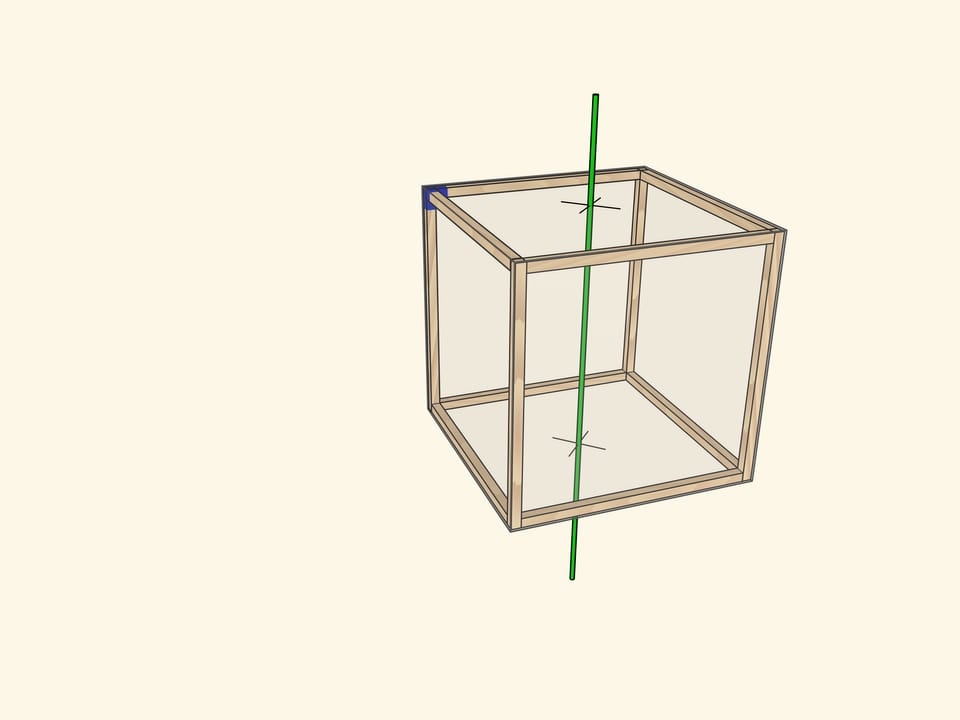
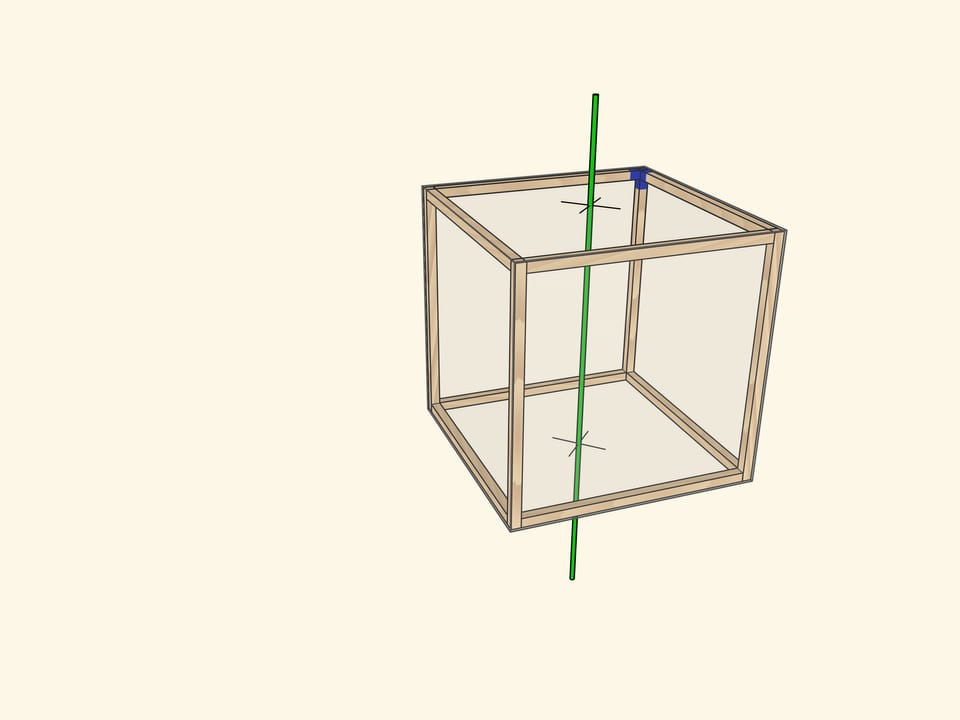
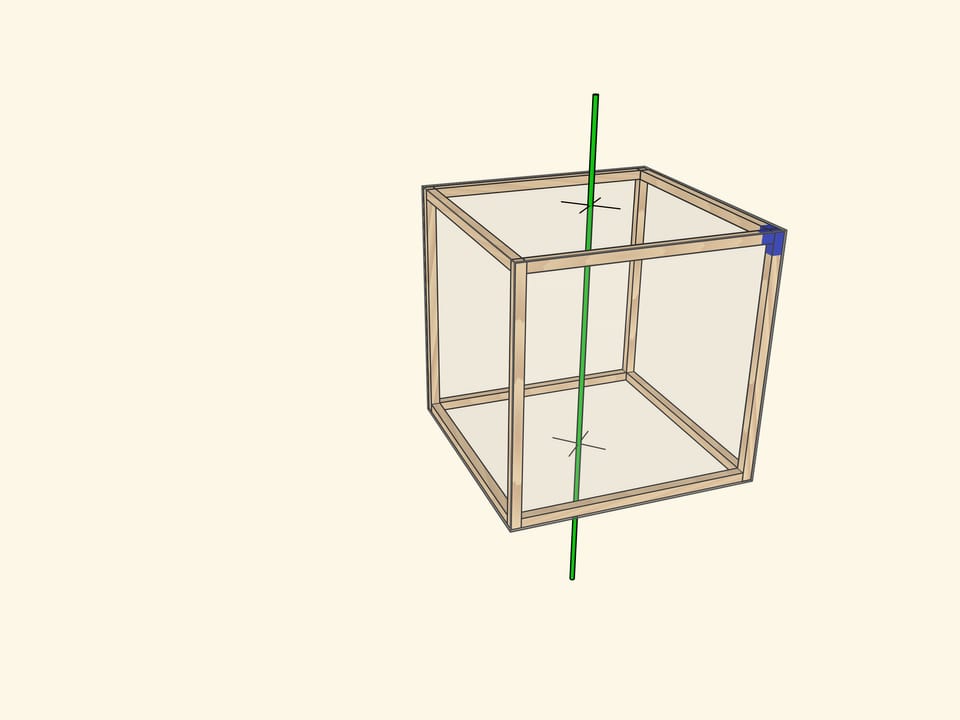
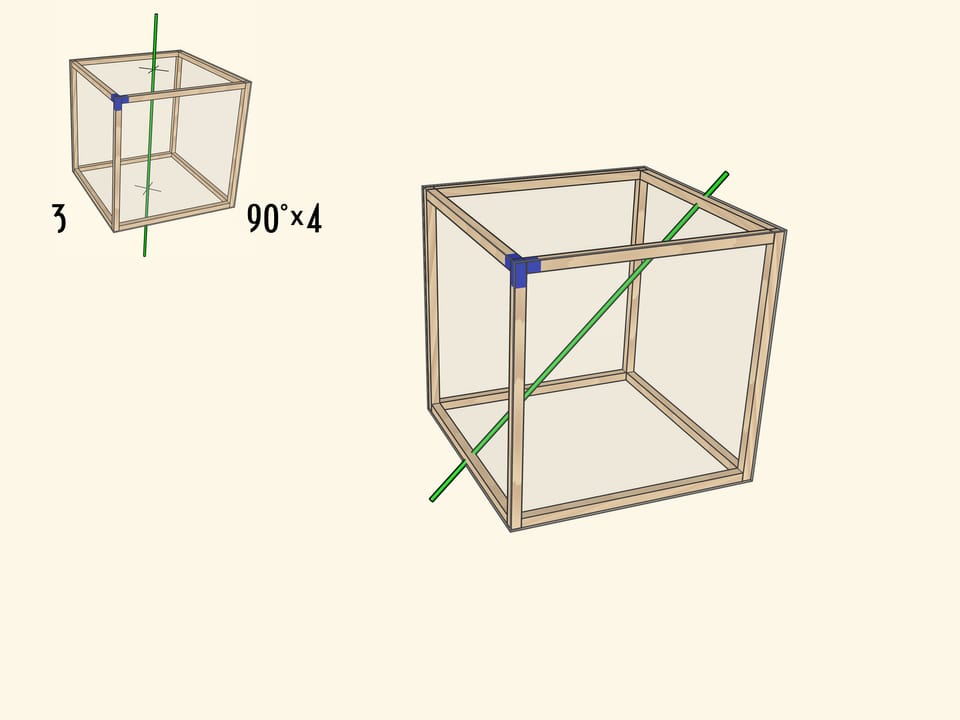
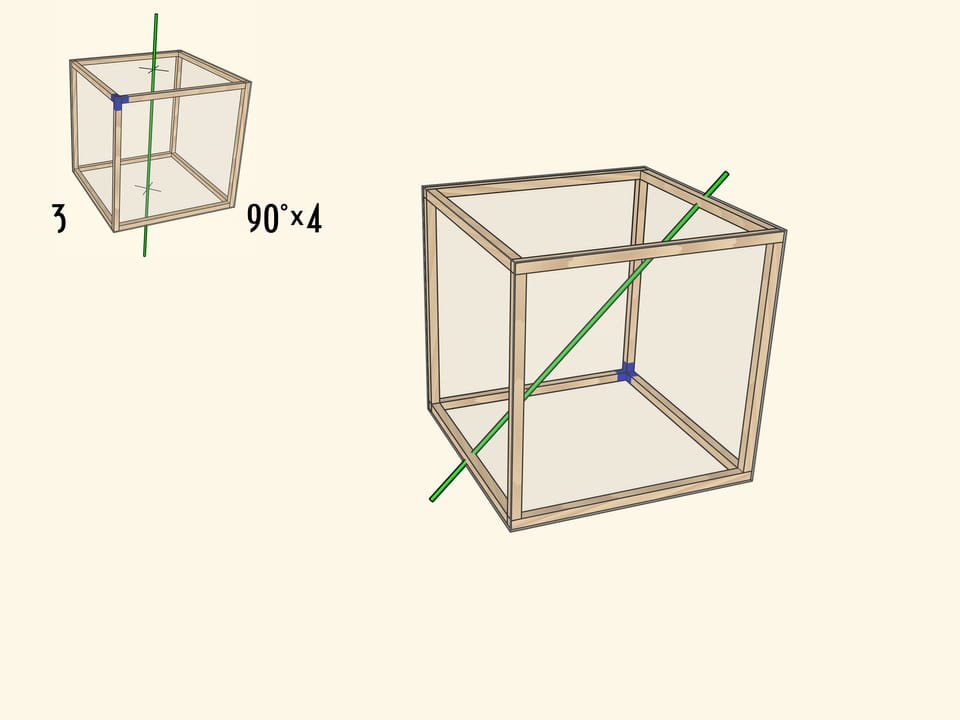
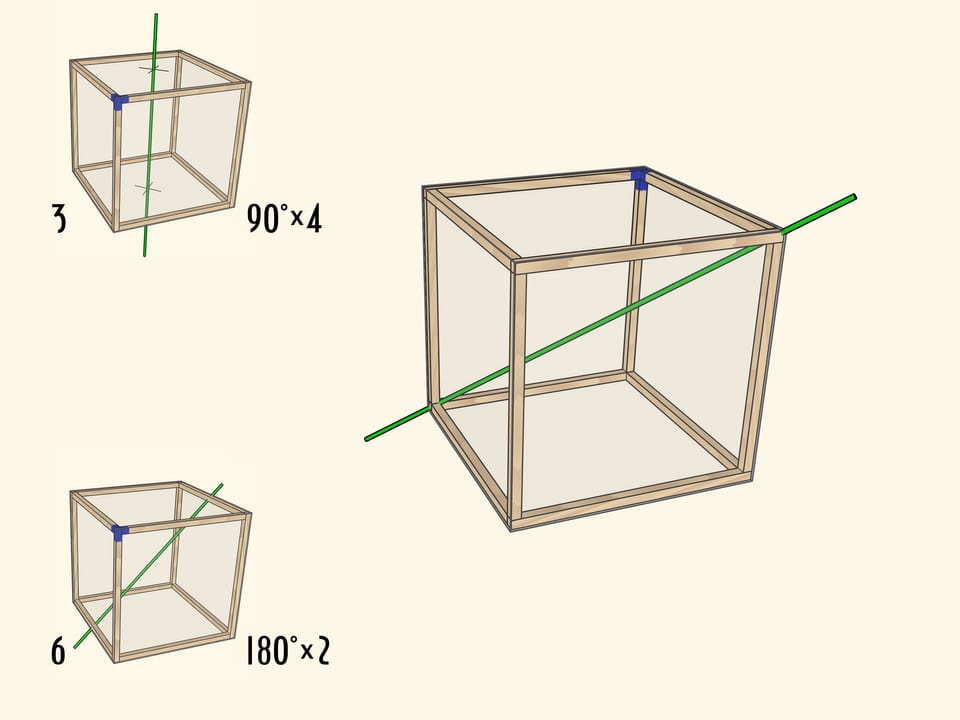
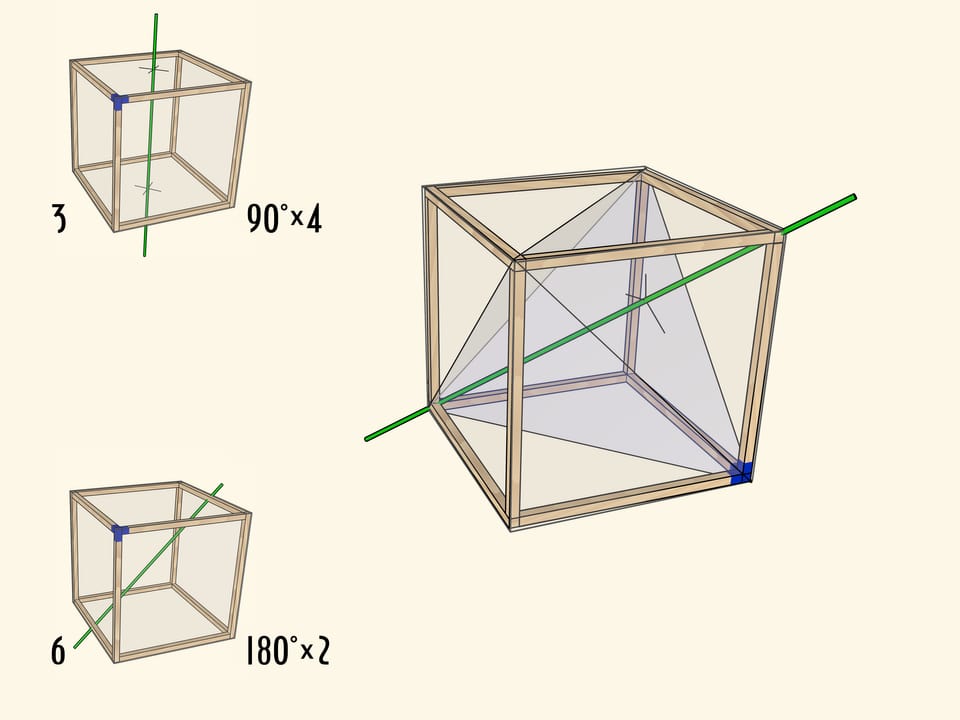
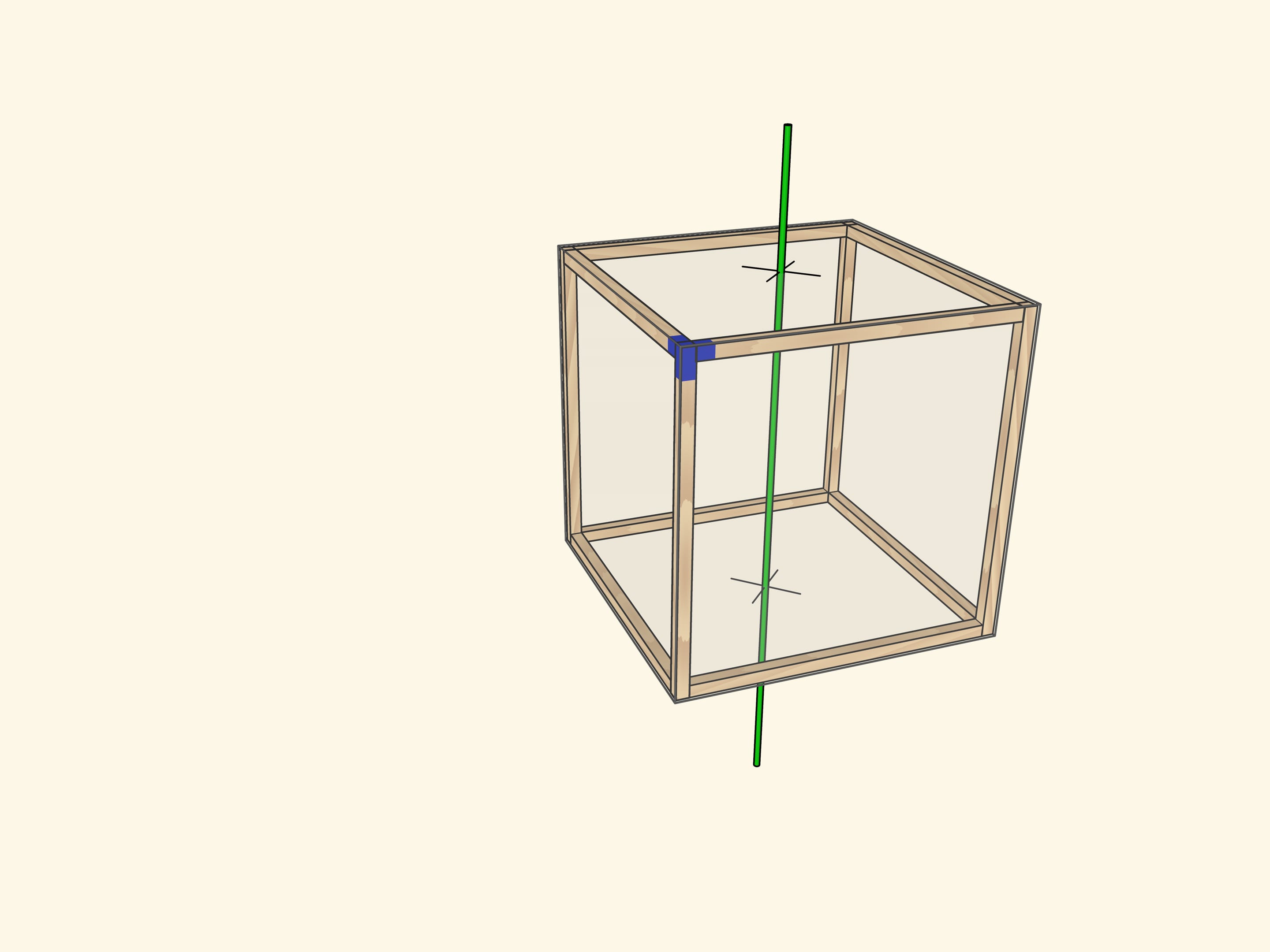
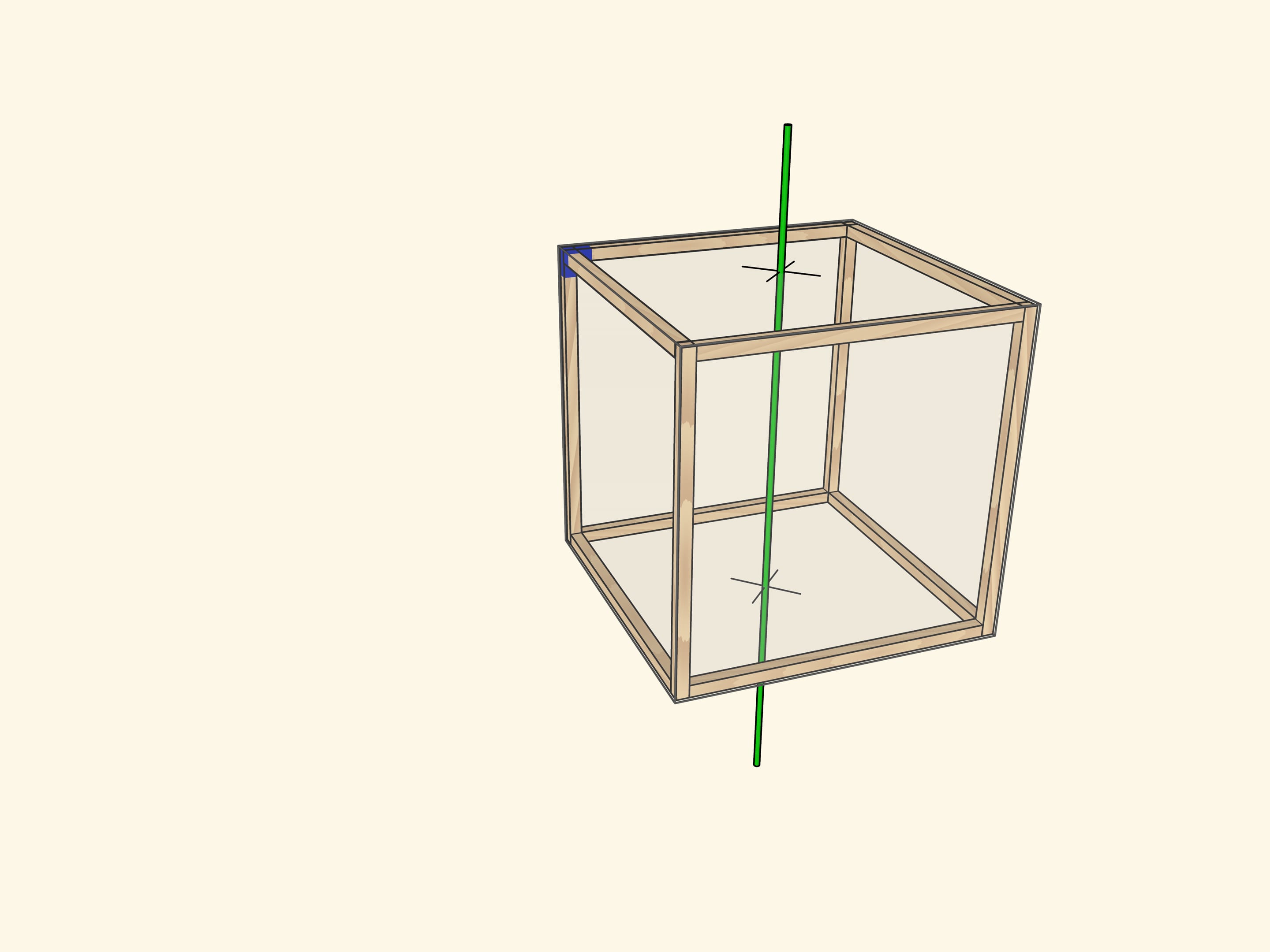
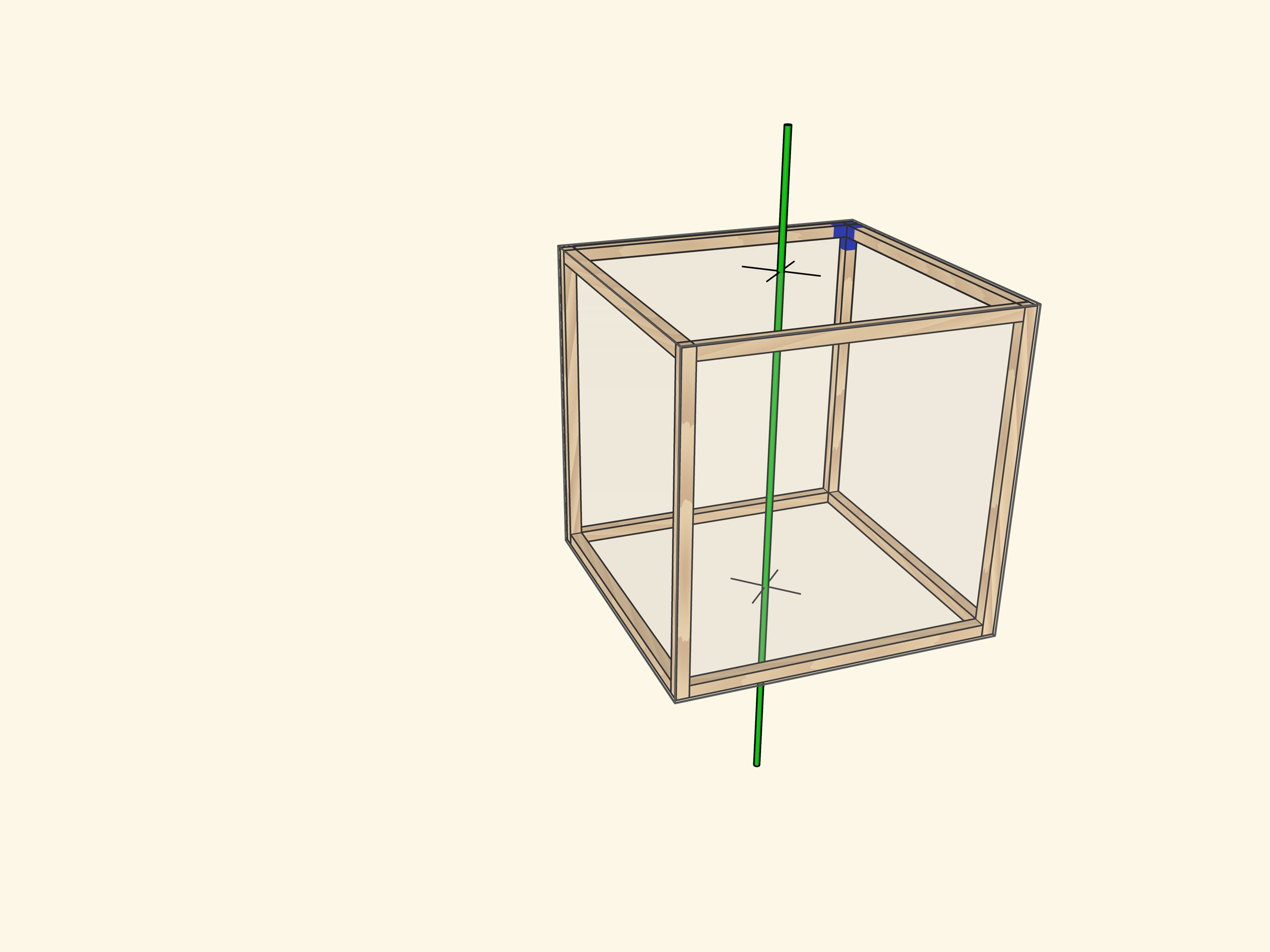
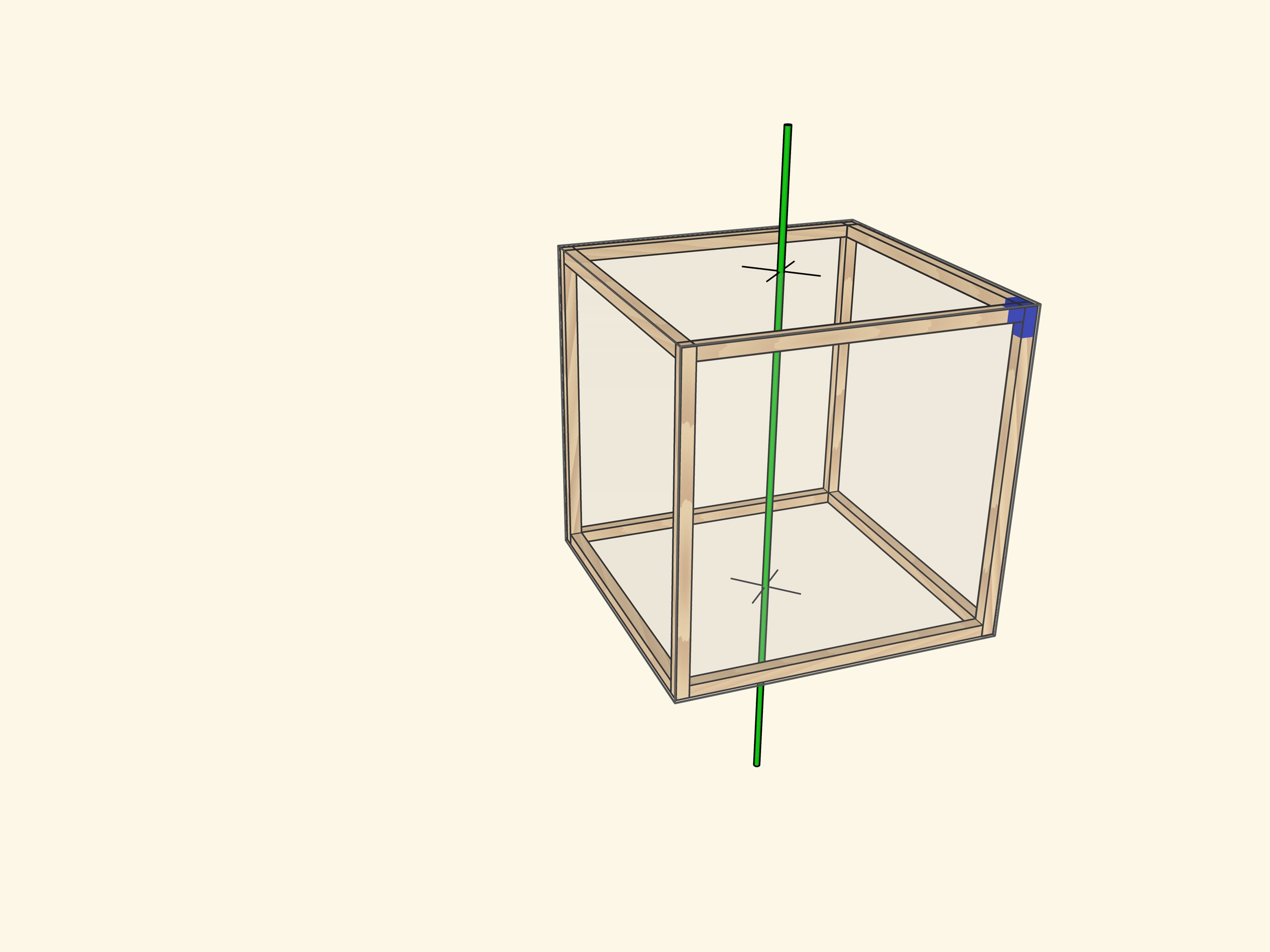
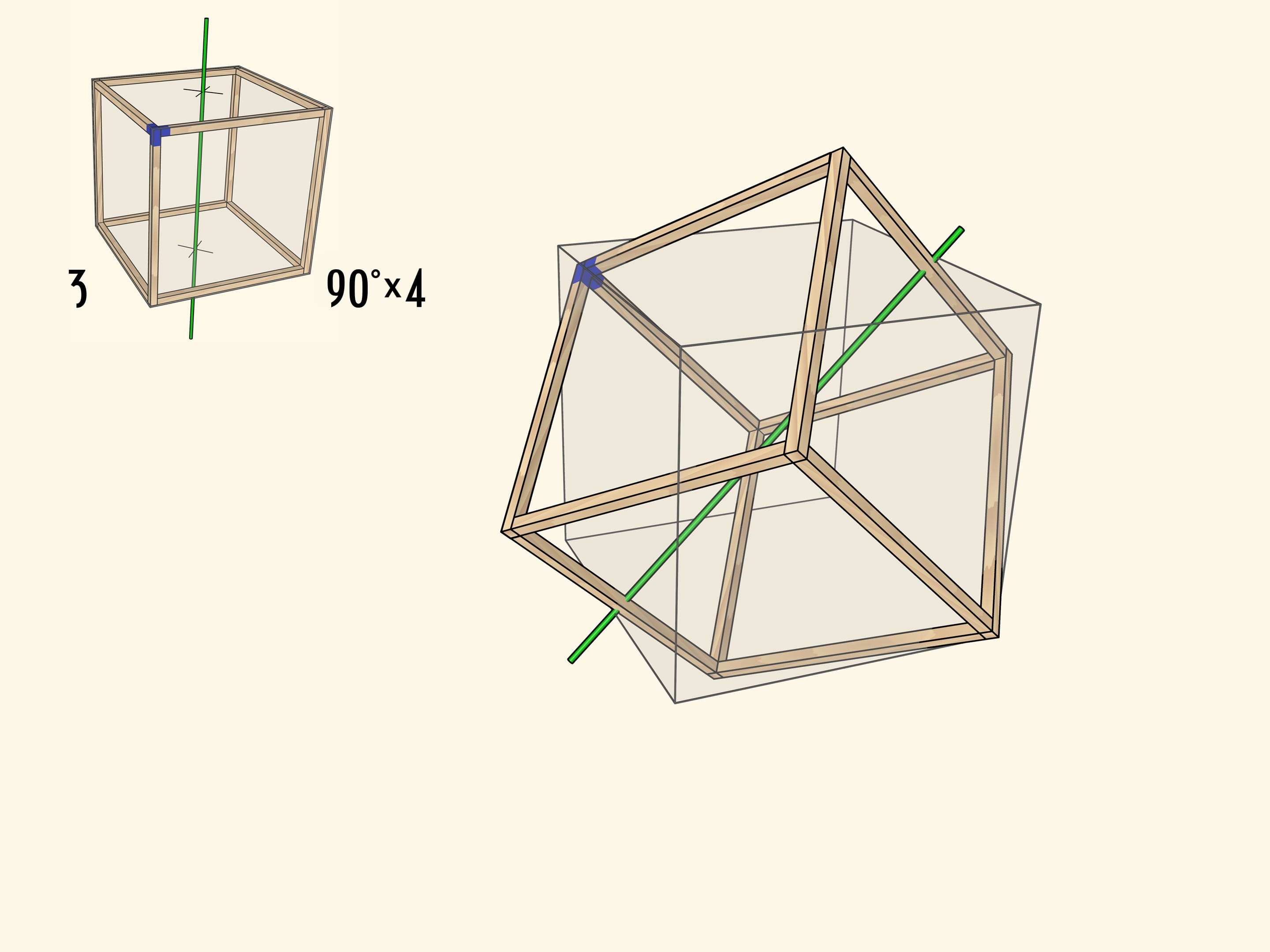
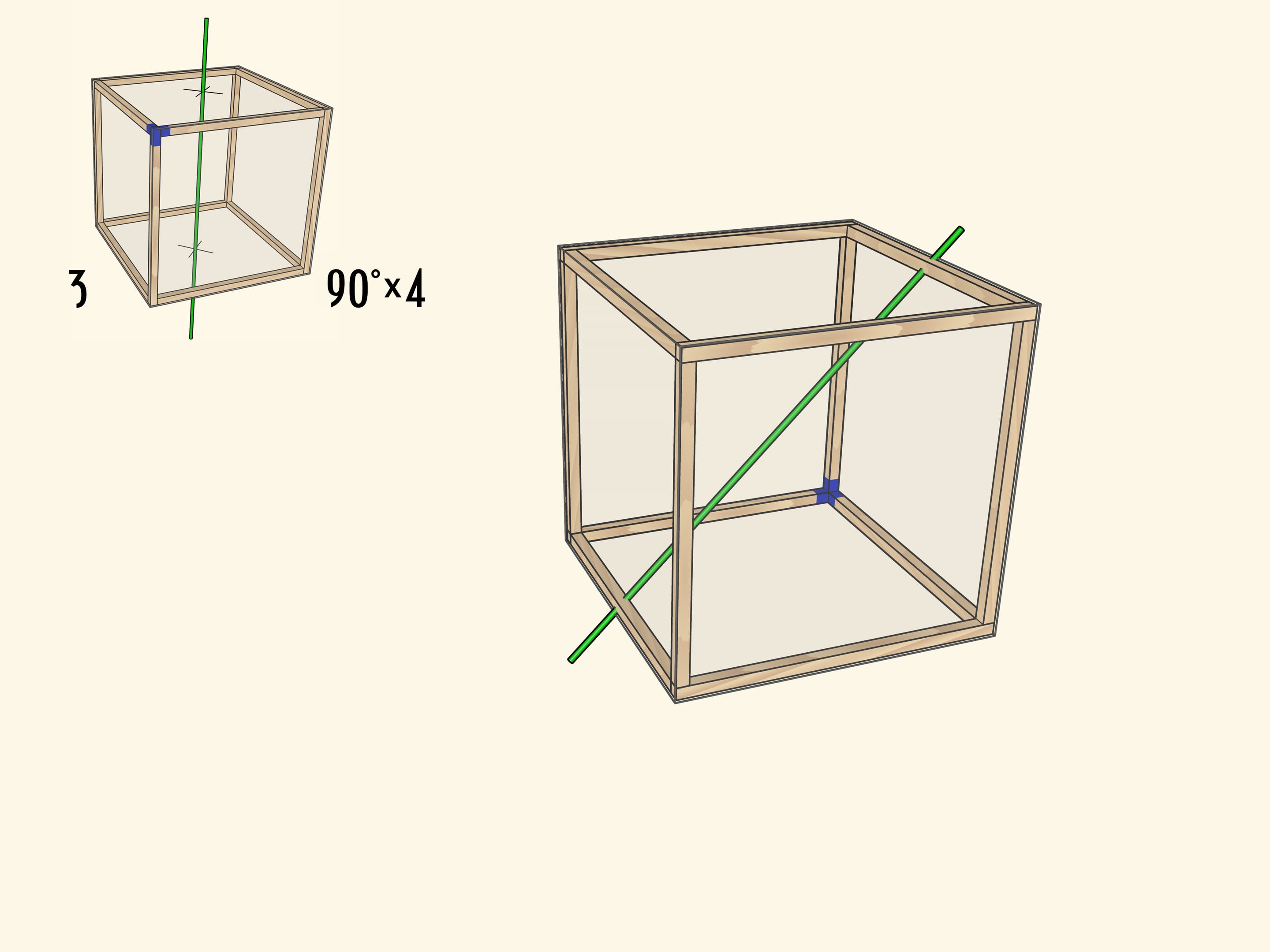
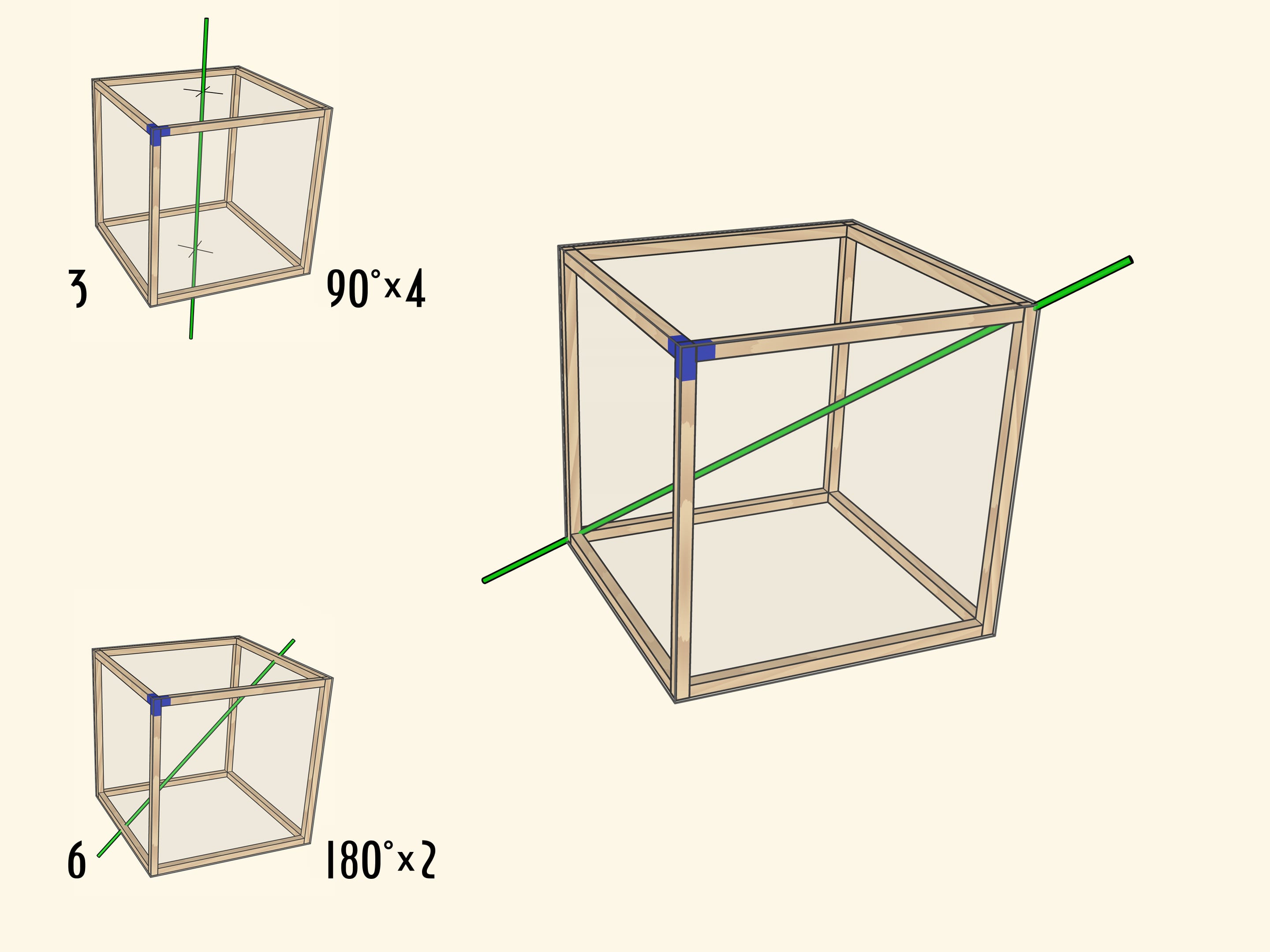
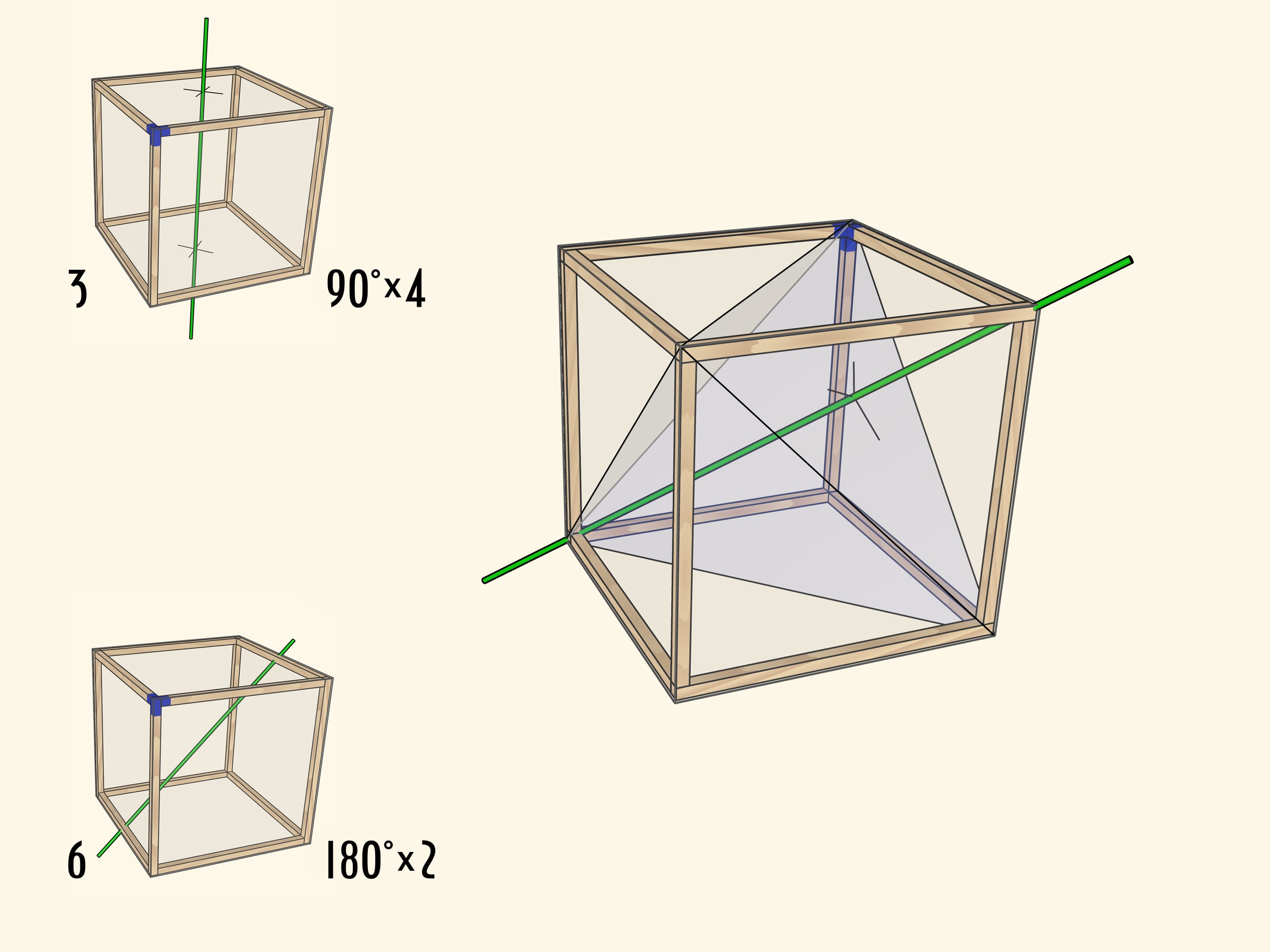
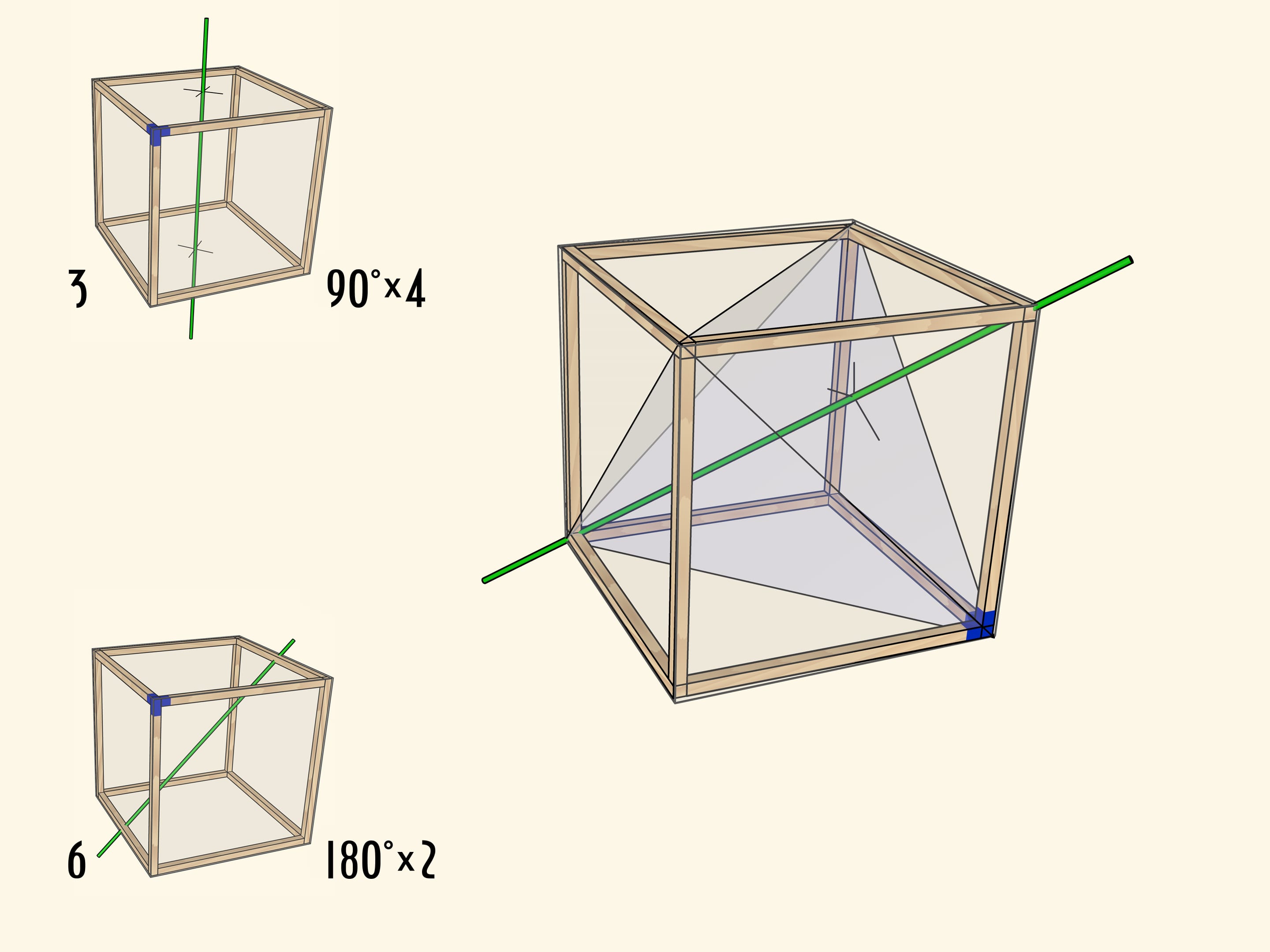
Самая оче­вид­ная ось про­хо­дит через цен­тры про­ти­вопо­лож­ных гра­ней куба. При пово­роте на $90^\circ$ куб пере­хо­дит в себя, а после четырёх таких пово­ро­тов ока­зы­ва­ется в исход­ном положе­нии. Осей чет­вёр­того порядка у куба $3$: столько же, сколько пар про­ти­вопо­лож­ных гра­ней.

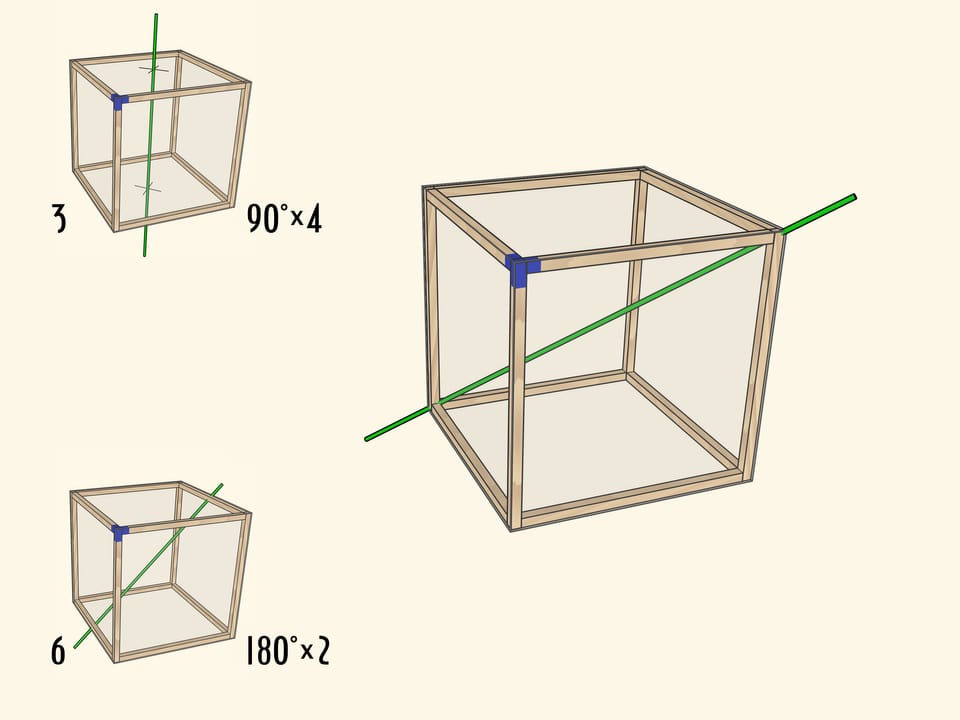
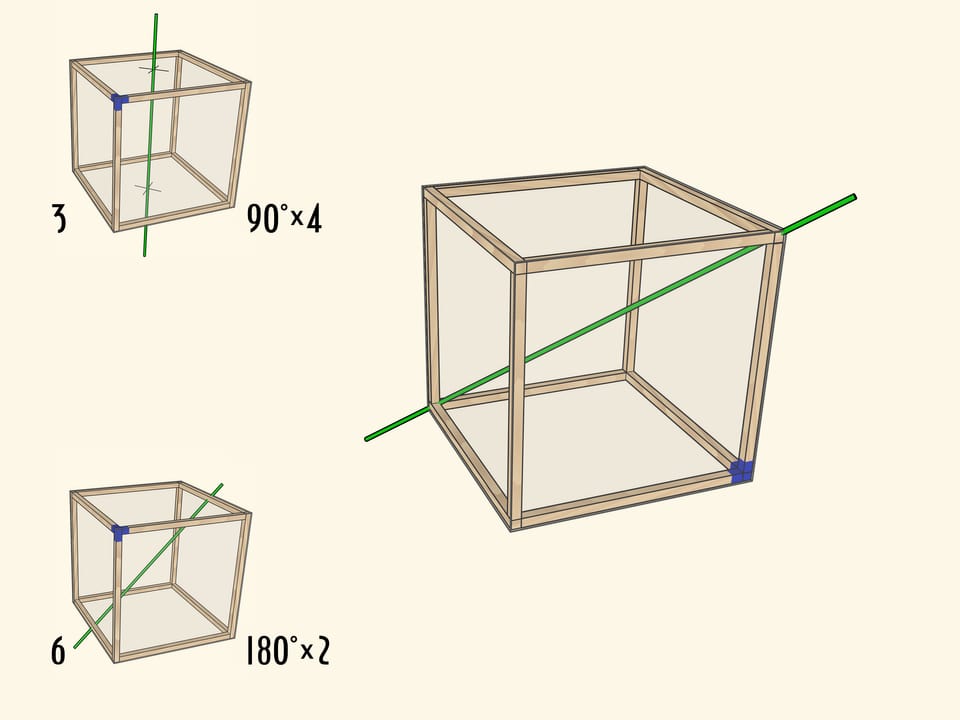
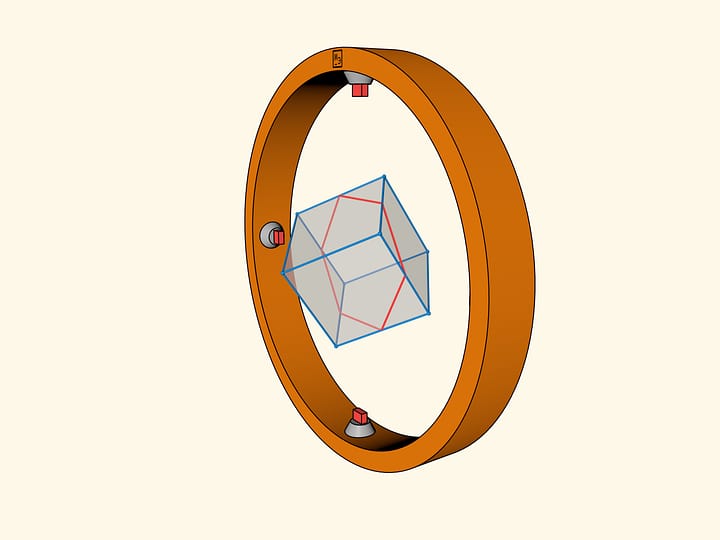
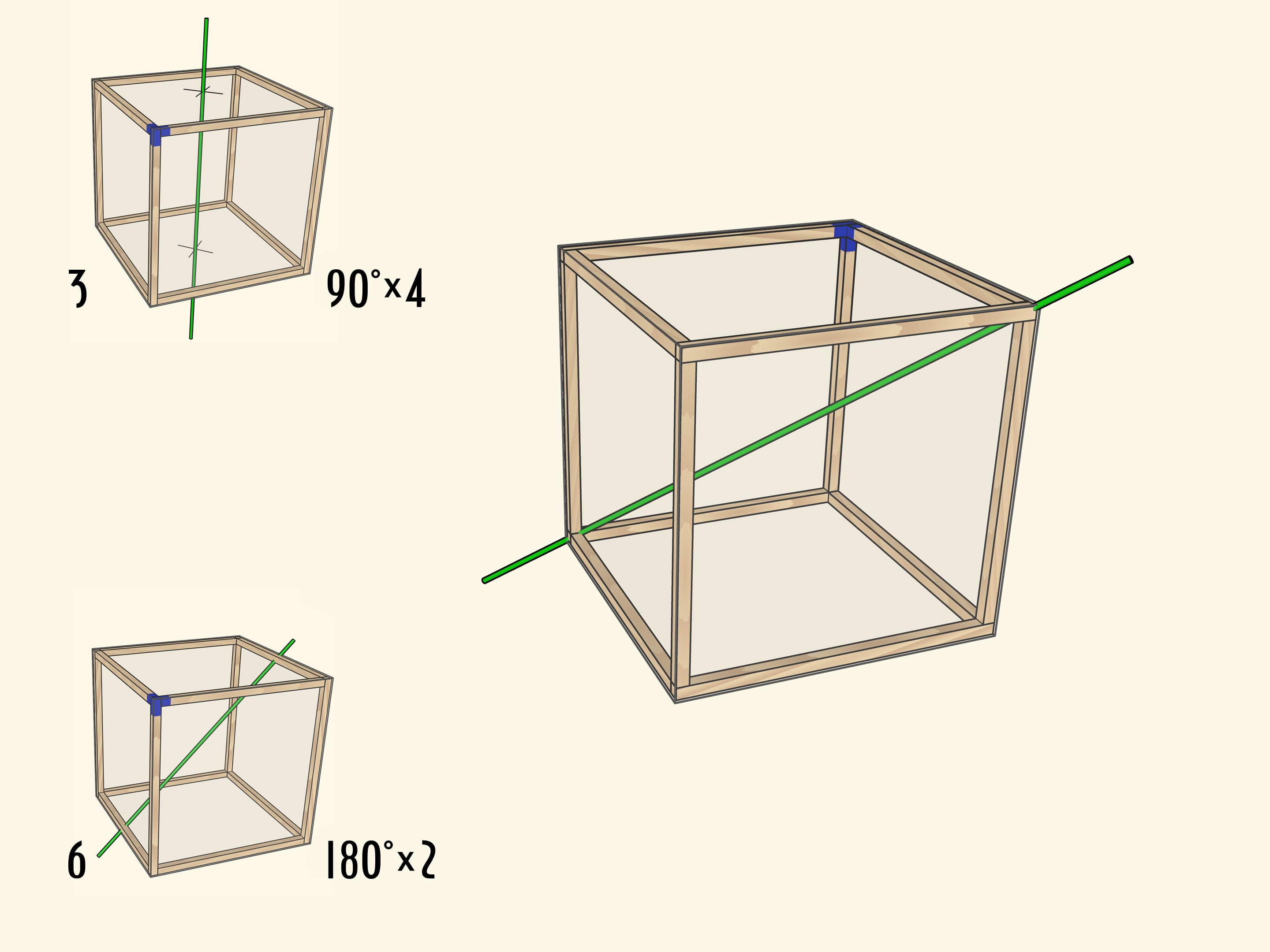
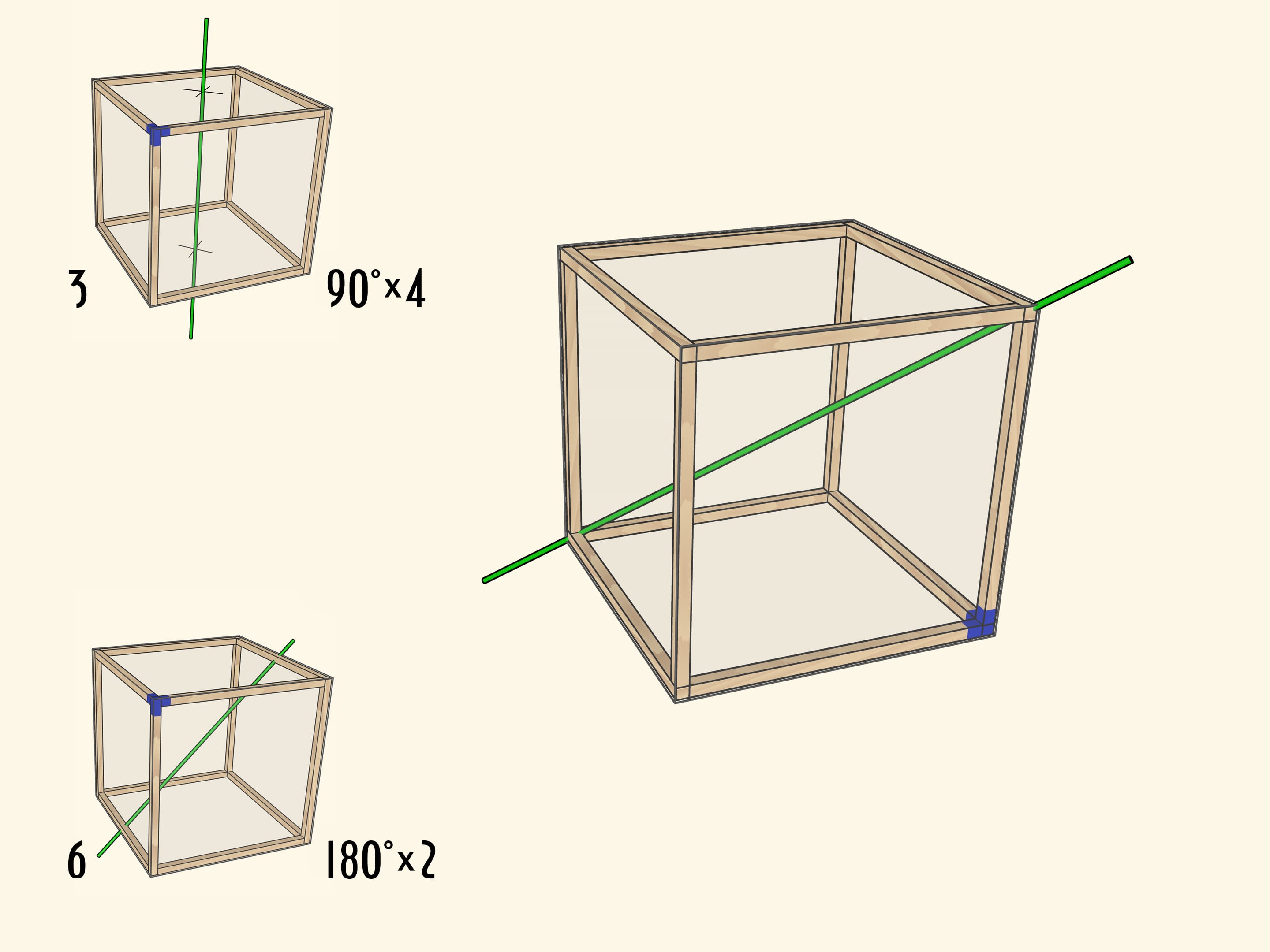
Менее оче­видно, что у куба есть ось вто­рого порядка — ось, про­хо­дящая через сере­дины про­ти­вопо­лож­ных рёбер куба. Таких осей всего $6$.

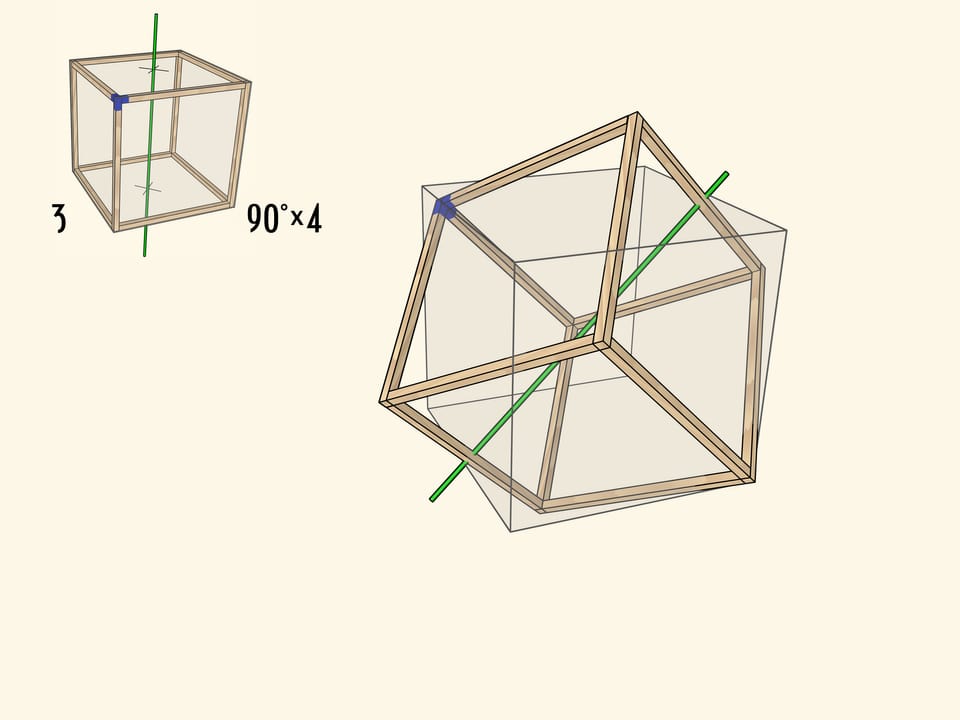
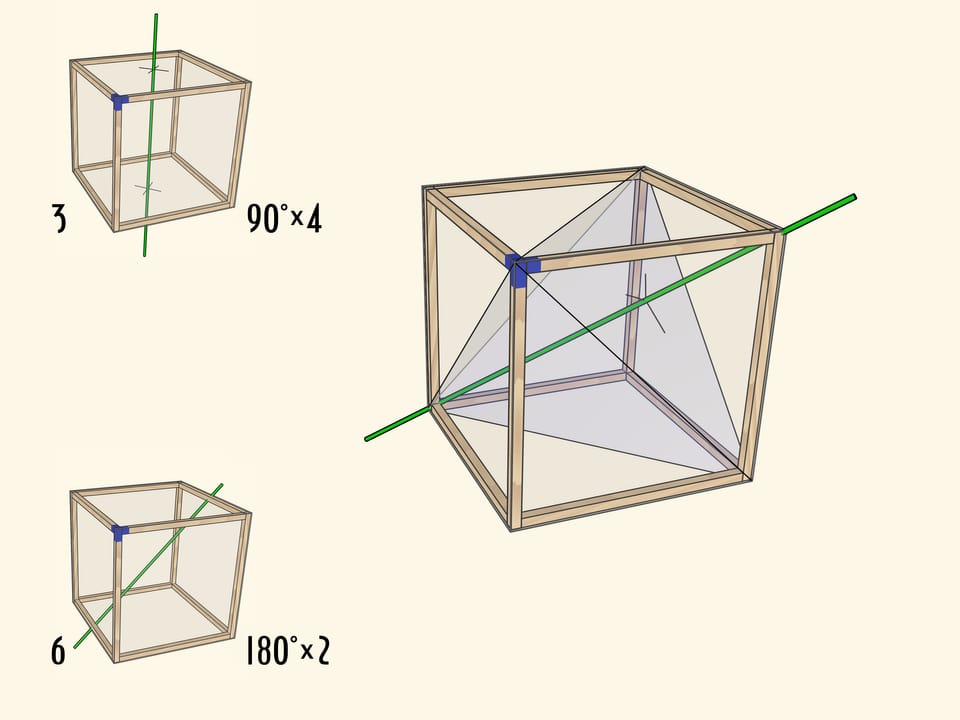
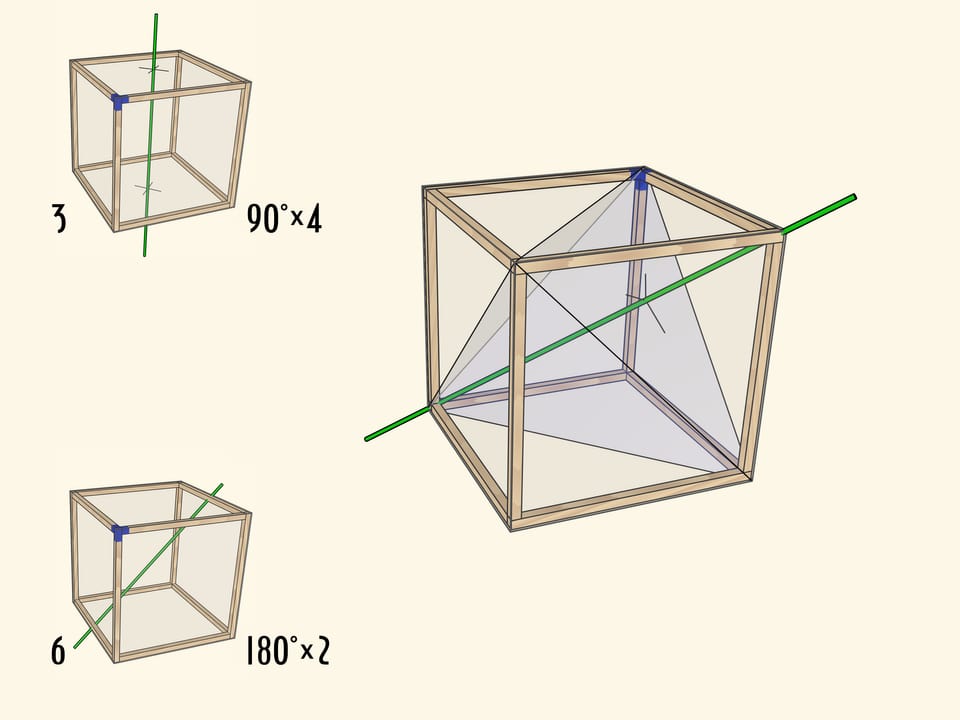
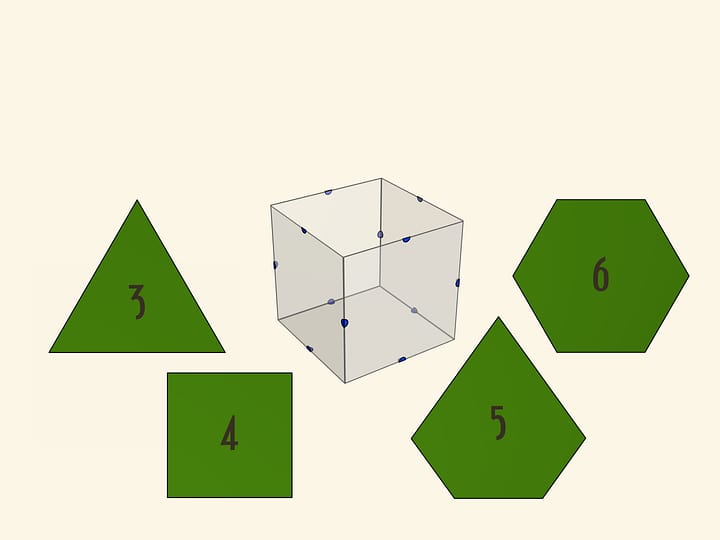
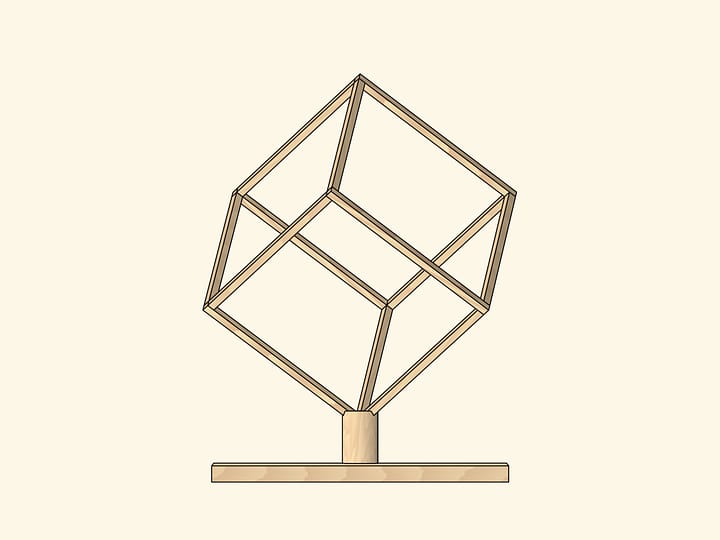
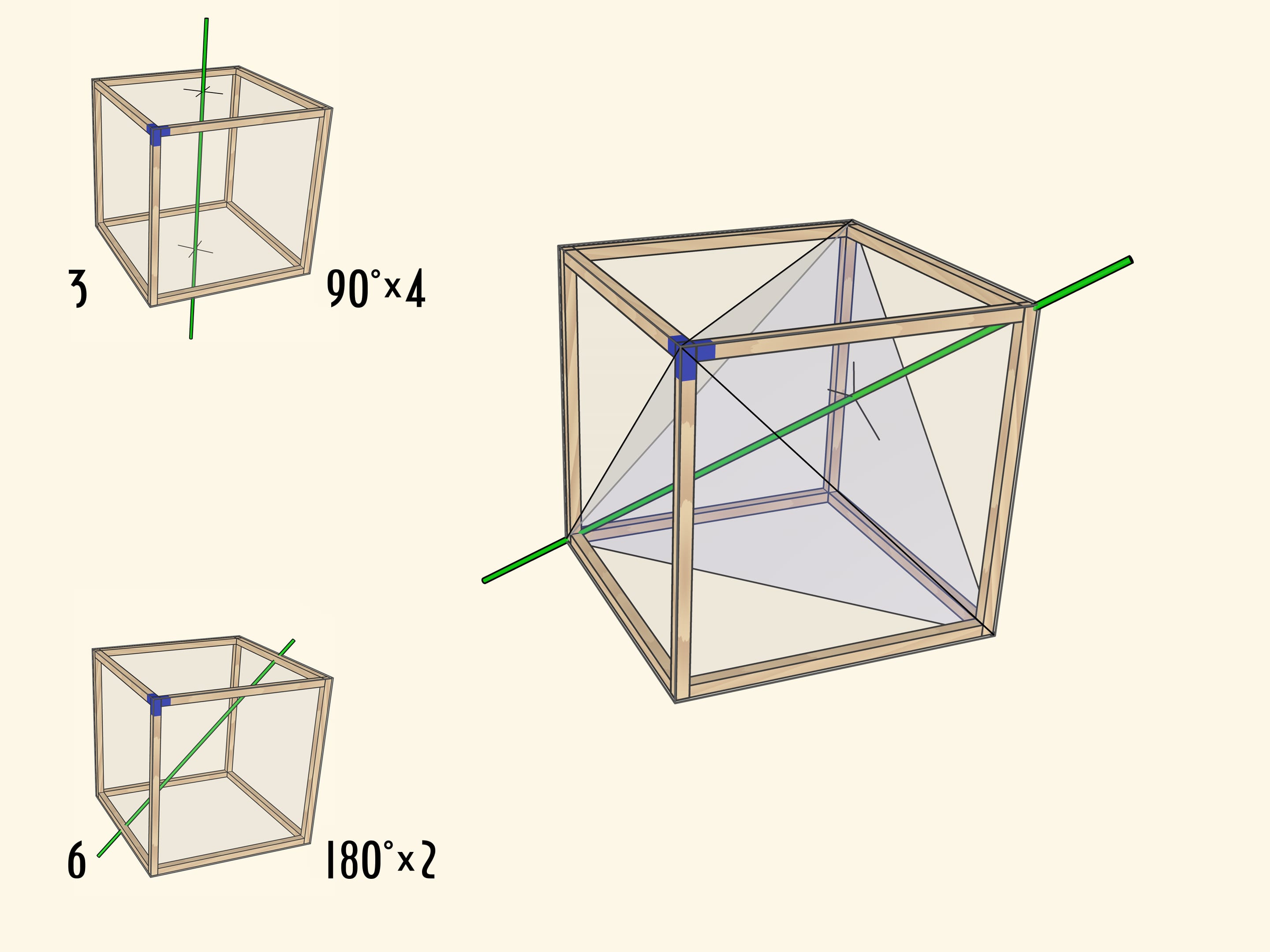
Ну и совсем уже неоче­видно на пер­вый взгляд, что у куба есть оси враще­ния тре­тьего порядка. Это диаго­нали куба.

Суще­ство­ва­ние таких осей ста­но­вится оче­вид­ным, если вспом­нить, что в куб ⁠⁠можно ⁠⁠впи­сать пра­виль­ный тет­раэдр.

Каж­дый тип пово­рота можно пред­ста­вить как отдель­ную модель с закреп­лён­ной в плос­ко­сти осью (под соот­вет­ствующим углом) и кубом, вращающимся на соот­вет­ствующие этой оси углы.

Пере­чис­лены все враще­ния, пере­во­дящие куб в себя, — других нет. А сово­куп­ность всех пово­ро­тов многогран­ника обра­зует группу: любые два после­до­ва­тельно сде­лан­ные пово­рота являются каким-то из уже пред­став­лен­ных пово­ро­тов. Попро­буйте понять, что будет компо­зицией двух пово­ро­тов отно­си­тельно каких-то несовпа­дающих осей, пово­ро­том вокруг какой оси и на какой угол. Коли­че­ство раз­лич­ных пово­ро­тов, пере­во­дящих куб в себя — поря­док группы — равно $24.$

Вме­сте с тож­де­ствен­ным это $3$ пово­рота на $90^\circ$ вокруг каж­дой из $3$ осей чет­вёр­того порядка (а чет­вёр­тый пово­рот — уже тож­де­ствен­ное пре­об­ра­зо­ва­ние), по $2$ пово­рота на $120^\circ$ вокруг $4$ осей тре­тьего порядка и пово­роты на $180^\circ$ вокруг $6$ осей вто­рого порядка: $1+3\cdot3+4\cdot 2+6\cdot1=24$. Заме­тим, что $24=4!$ — коли­че­ство пере­ста­но­вок четырёх пред­ме­тов, так как каж­дому пово­роту куба соот­вет­ствует пере­ста­новка на множе­стве его диаго­на­лей.