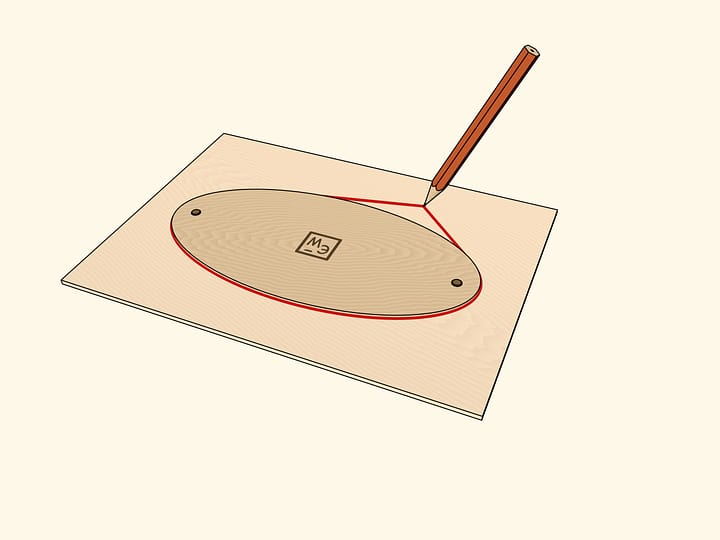
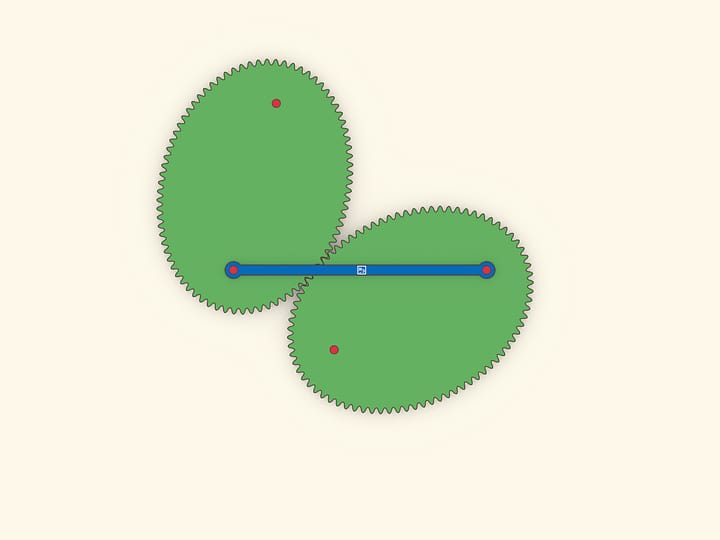
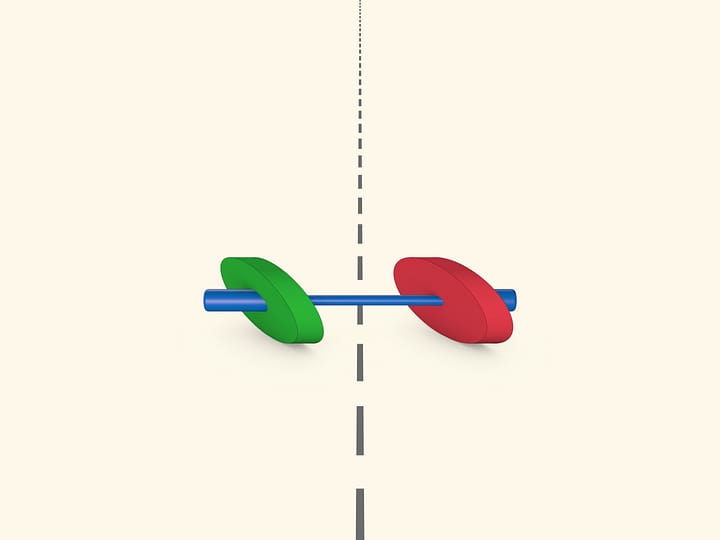
Сечение прямого кругового конуса, пересекающее все его образующие, — эллипс или, как частный случай, круг. Простая модель — конус, рассечённый по эллипсу на две держащиеся на магнитах части, — показывает, что эллипс является центрально симметричной фигурой.
Эллипс можно получить не только как сечение конуса, но и как сечение (прямого кругового) цилиндра плоскостью, непараллельной его оси. Соединение конуса и цилиндра по одному и тому же эллипсу приводит к простому, но интересному наблюдению — их оси не совпадают. Это, например, следует из того, что ось прямого кругового конуса не проходит через центр эллипса, если только это не вырожденный случай, окружность.
«Обратим» знание, что у прямого кругового конуса есть сечение в виде эллипса. Пусть основанием конуса будет эллипс, а сам конус будет наклонным. У такого конуса есть сечение в виде круга — достаточно представить прямой круговой конус наклонённым и «срезанным горизонтально».
Этот факт учитывается при дублировании запрещающих дорожных знаков на асфальте. Круглый знак ограничения скорости рисуют вытянутым — в виде эллипса, а водитель, смотрящий на такую картинку, в какой-то момент видит её в виде круга.
В тексте обдуманно допускалась некоторая неточность. Для себя стоит аккуратно понимать, что эллипс — это кривая, а круг — это фигура. И сечением конуса является фигура, ограниченная эллипсом, а эллипс является сечением конической поверхности.