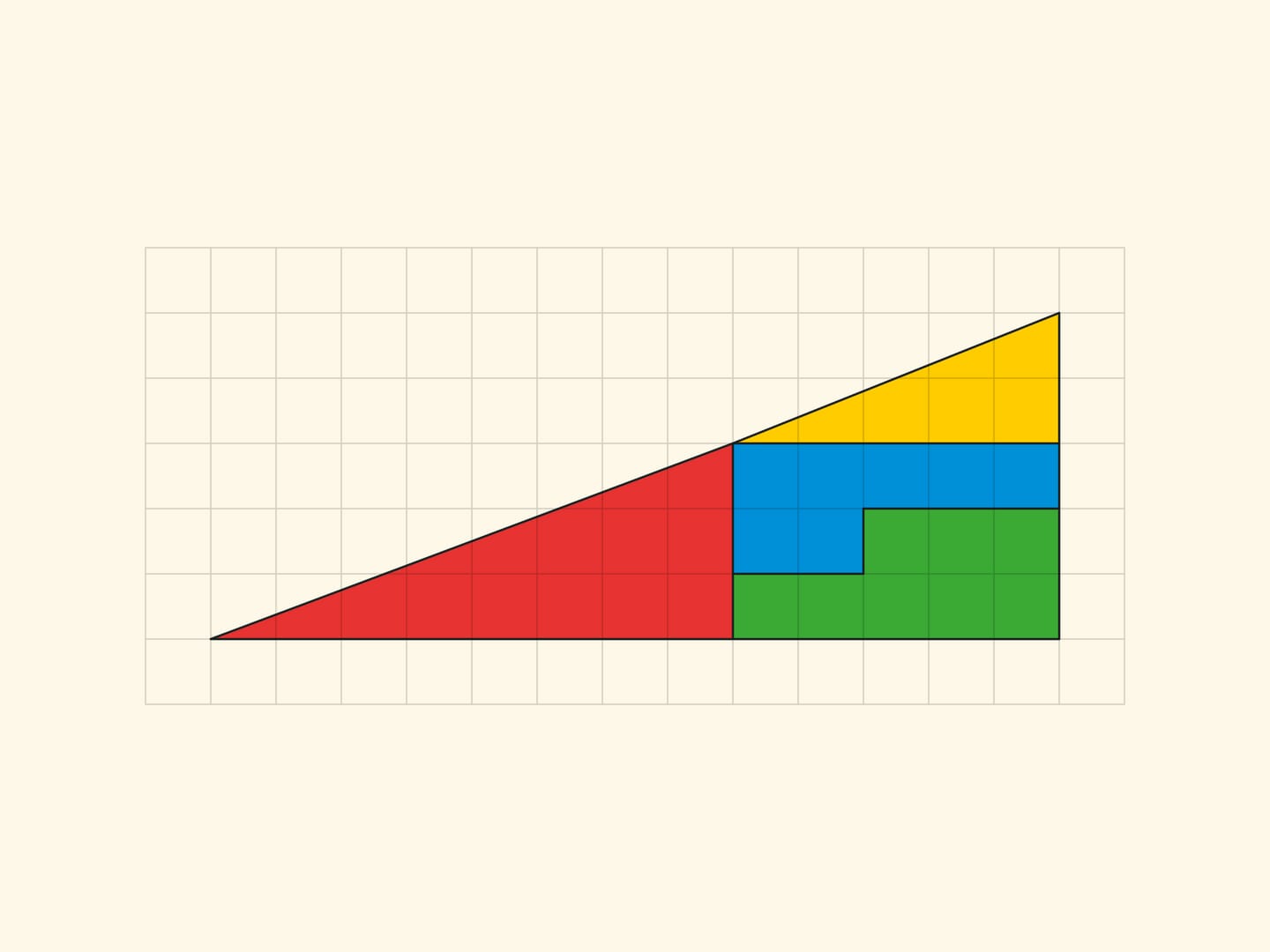
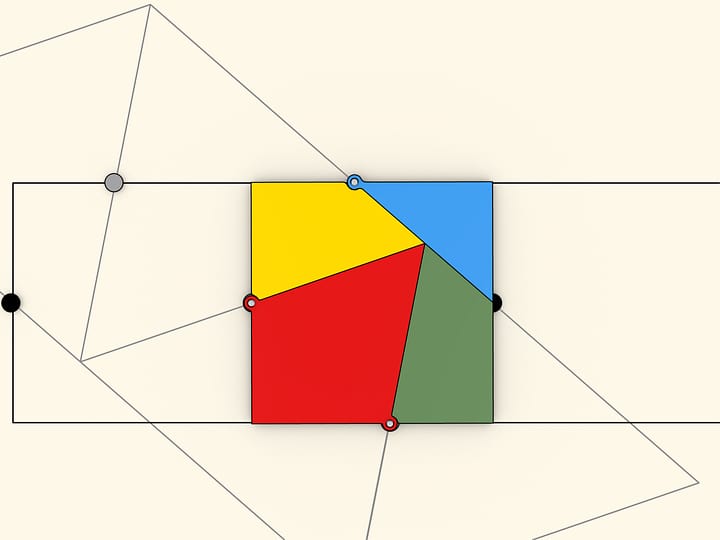
Квадрат $8\times 8$ можно разрезать на четыре части из которых складывается… прямоугольник $5\times 13$ площадью $65!$
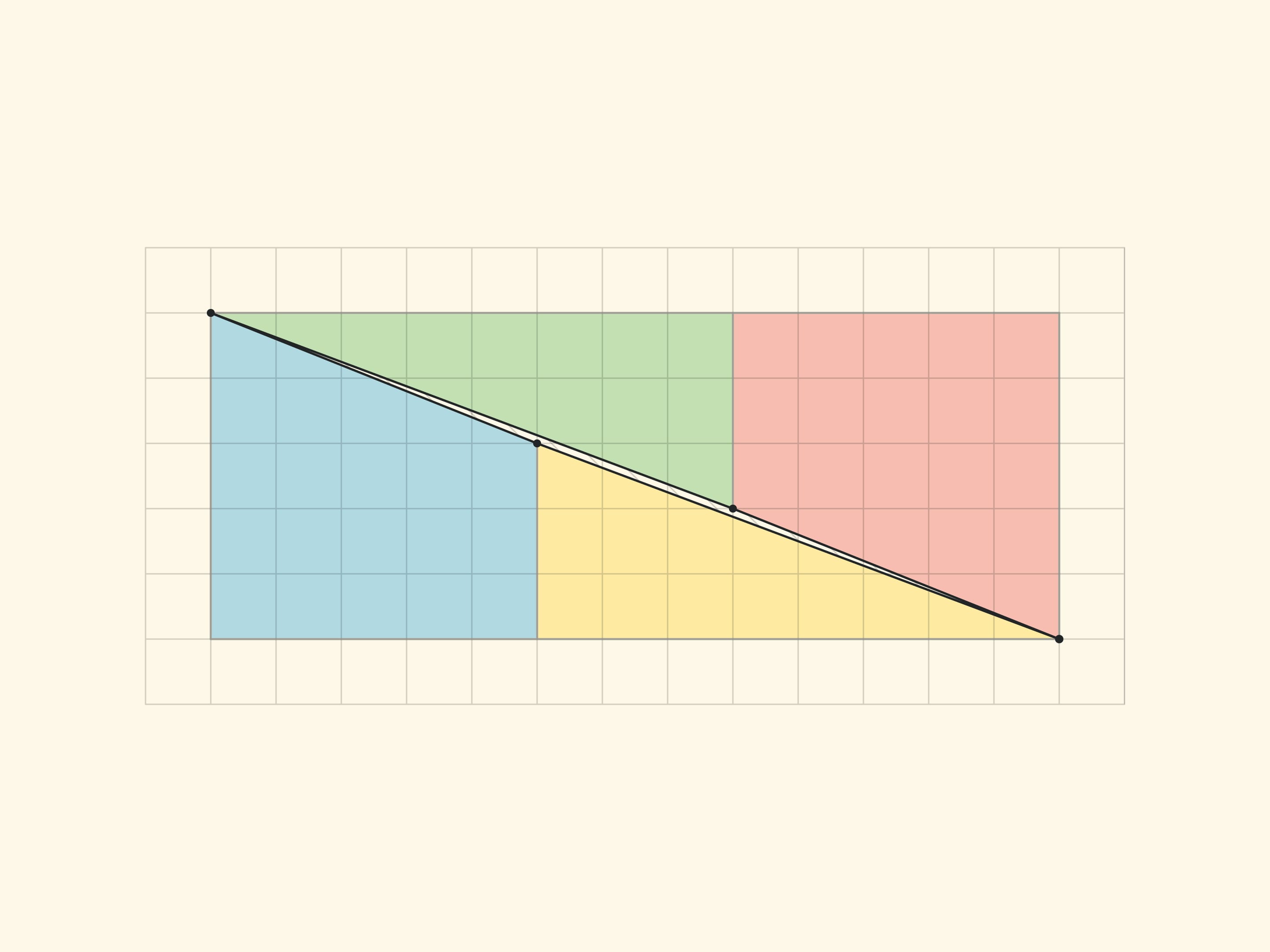
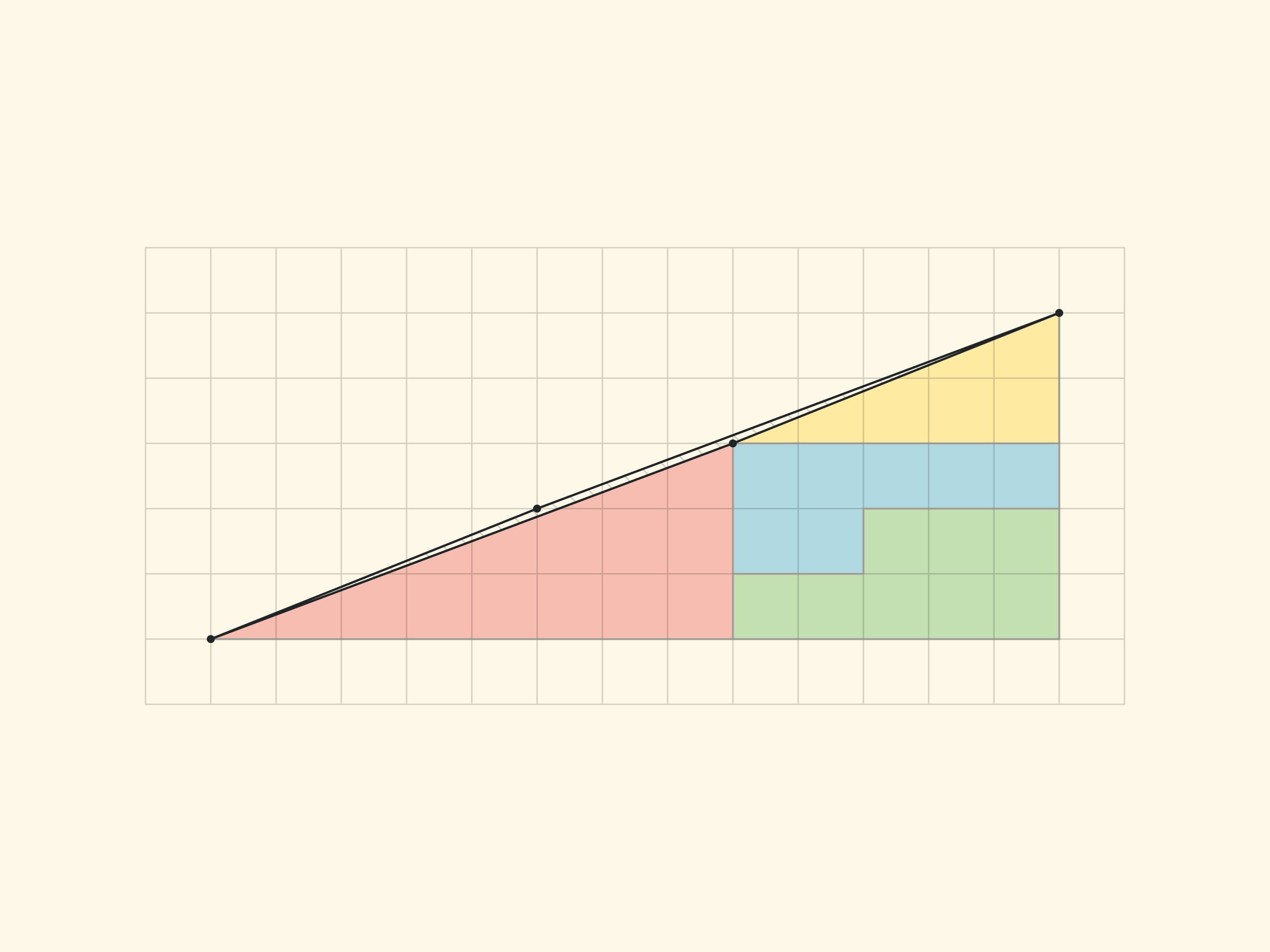
Ещё один известный геометрический софизм: прямоугольный треугольник с катетами $5$ и $13$ разрезается на четыре части, из которых складывается тот же прямоугольный треугольник, но уже с одной пустой клеткой!
Но постойте, площадь фигуры равна сумме площадей частей, из которых она составлена. Поэтому при перекладывании она не может измениться. В чём же нестыковка?
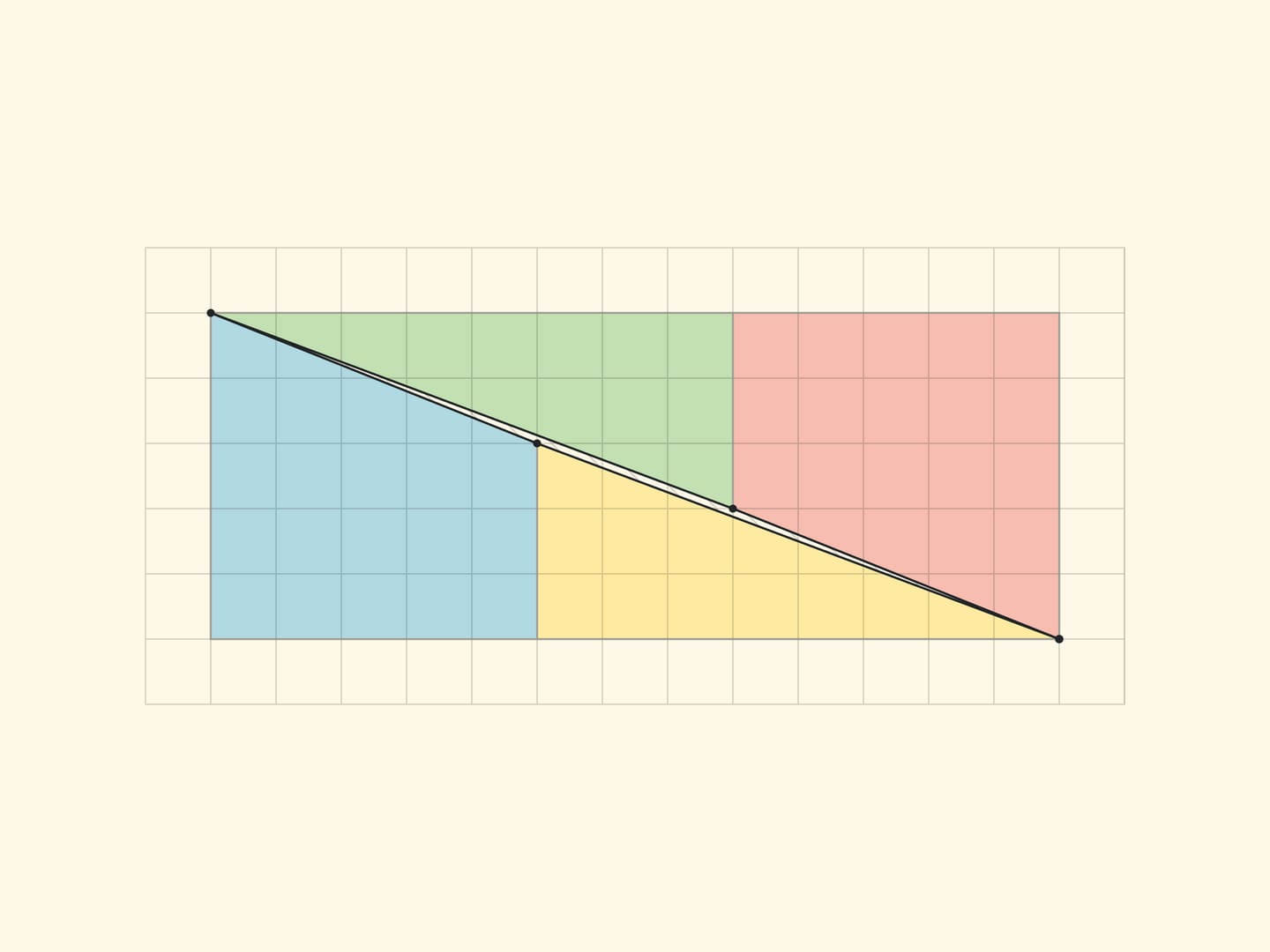
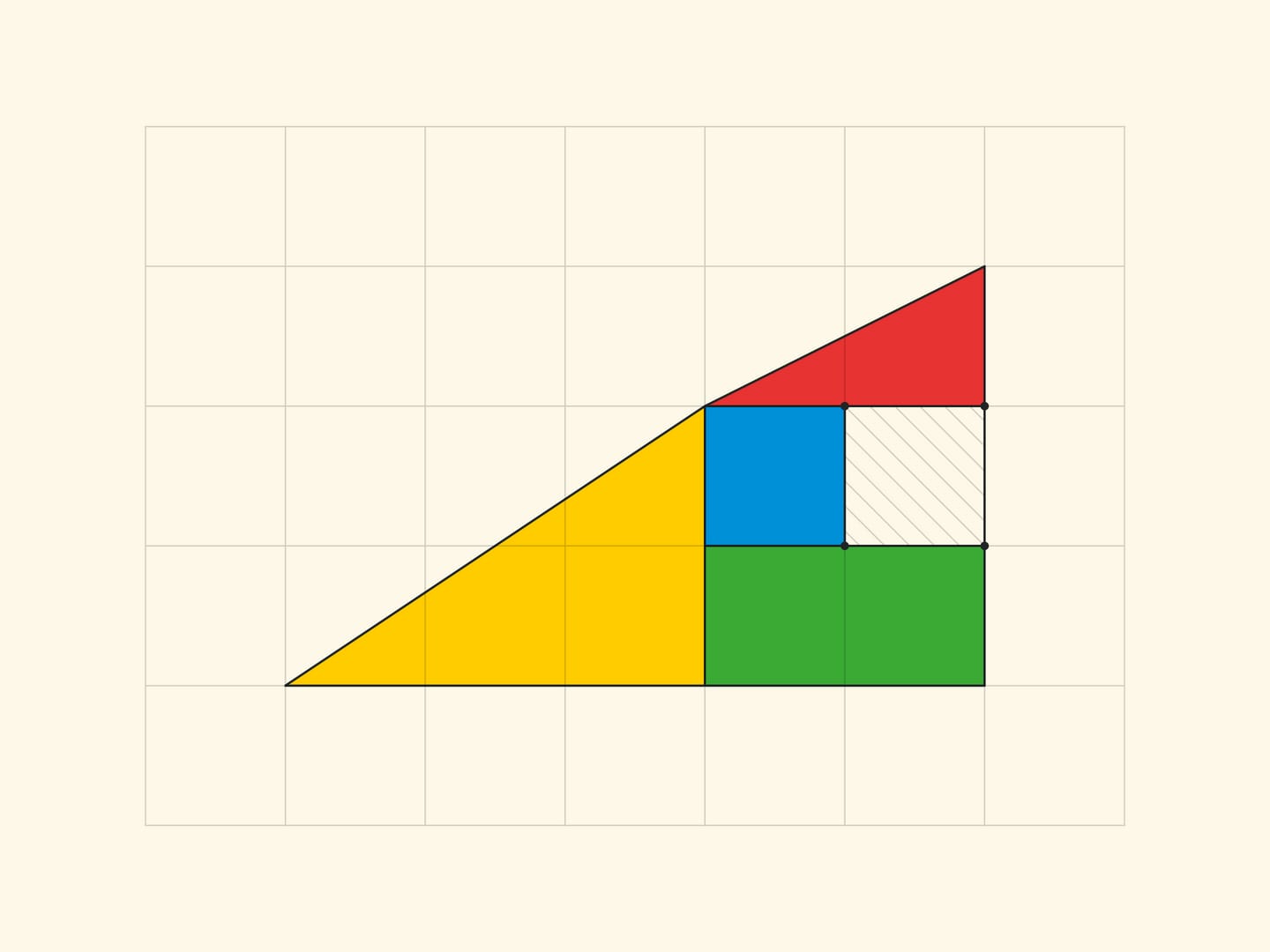
Объяснение парадокса в обоих случаях по сути одинаковое — рассматриваются не те фигуры, которые описывали. В «Парадоксе шахматной доски», представленном шахматистом и автором головоломок Сэмюэлем Лойдом в середине XIX века на шахматном конгрессе, честный квадрат перекладывается не в прямоугольник, а в прямоугольник без вытянутого, почти незаметного глазу параллелограмма единичной площади (вытянутого вдоль диагонали прямоугольника). В парадоксе с треугольниками, придуманном Мартином Гарднером в середине XX века, обе гипотенузы (исходного и получающегося треугольника) на самом деле не являются прямыми: составленная из них фигура также является параллелограммом единичной площади.
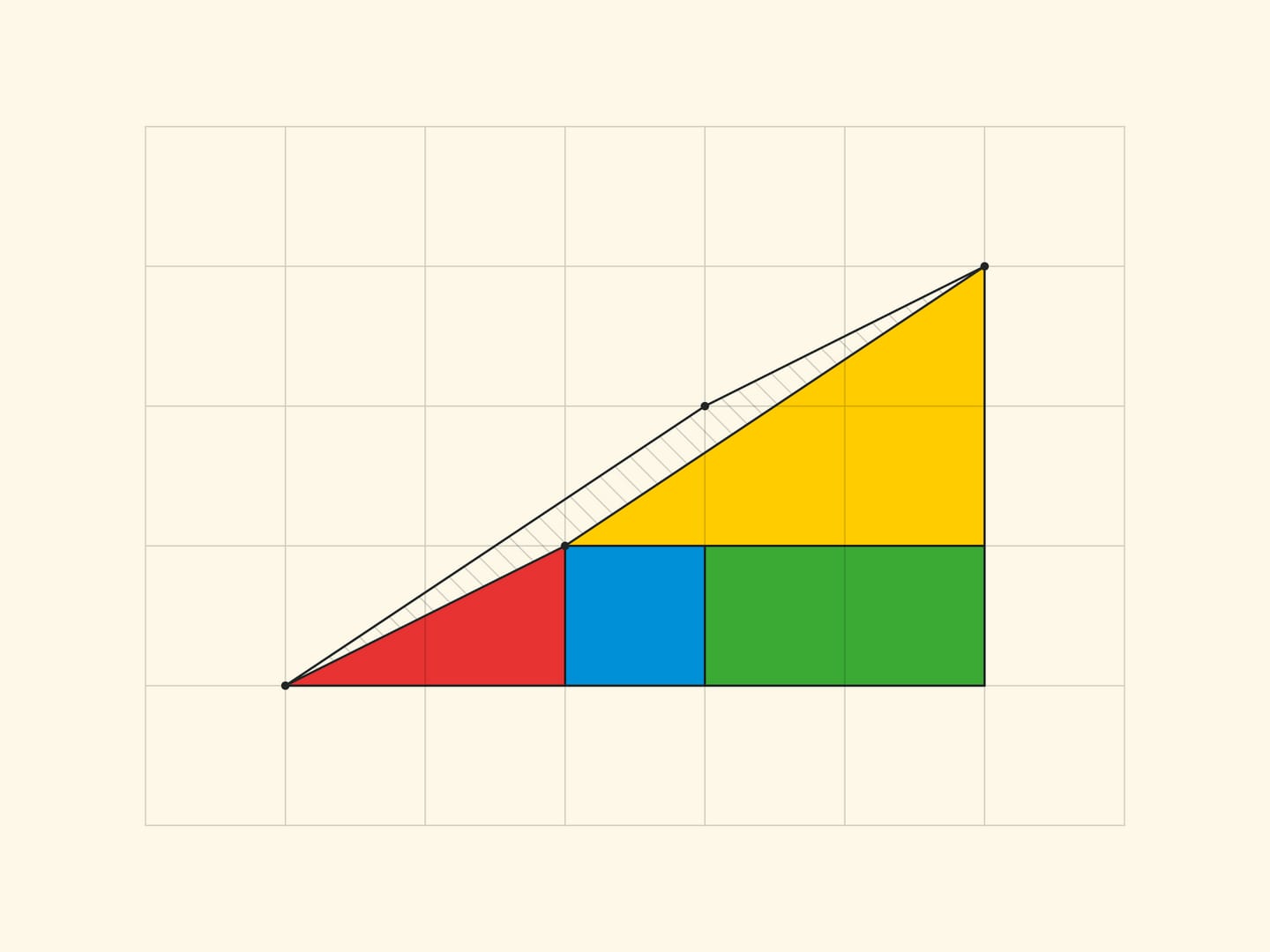
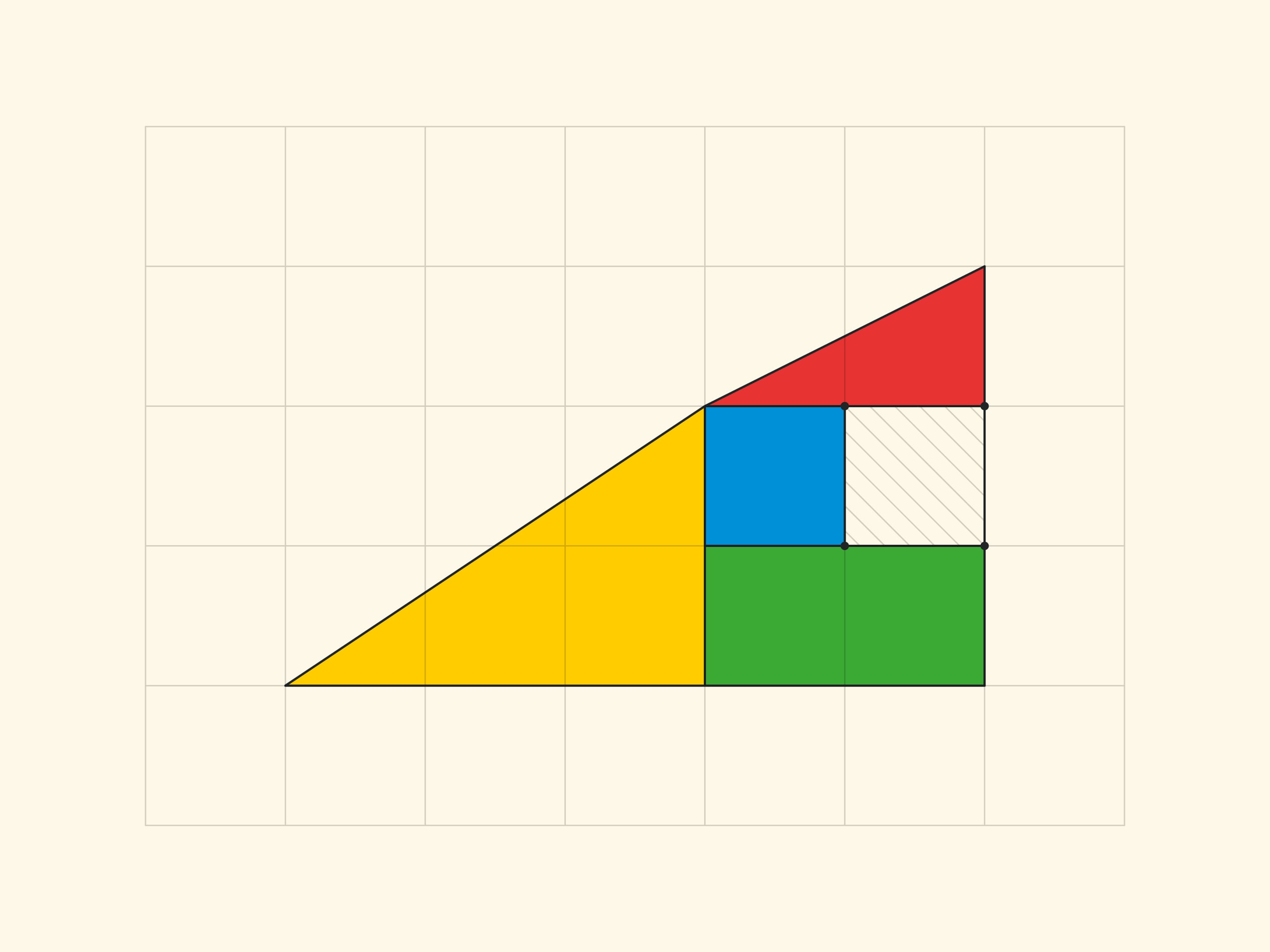
Чтобы было легче разглядеть этот параллелограмм, посмотрим на аналог «треугольника Гарднера» меньшего размера — со сторонами $3$ и $5$.
Все вершины всех частей лежат в узлах квадратной сетки. И в том, что границы частей не складываются в прямую линию, а образуют стороны параллелограмма (с вершинами в узлах), легко убедиться, посчитав по клеточкам наклон каждого отрезка. В прямоугольнике $5\times 13$ в жёлтом треугольнике отношение катетов равно $\tg \alpha=\dfrac{3}{8}$, а для синей трапеции тангенс «того же» угла равен $\dfrac{2}{5}$. Для софизма с треугольником: в варианте Гарднера $\dfrac{2}{5}\ne \dfrac{3}{8}$, в уменьшенном варианте $\dfrac{1}{2}\ne \dfrac{2}{3}$. Во всех случаях стороны параллелограмма, как и должно быть, попарно равны и параллельны. Вершины параллелограмма лежат в узлах сетки, а вот внутри параллелограмма нет ни одного узла. Что, впрочем, неудивительно, если вспомнить, что площадь равна единице и формулу Пика.
Разобравшись с нестыковкой, задумаемся, как конструировать подобные софизмы. Можно заметить, что встречавшиеся числа $1,$ $2,$ $3,$ $5,$ $8,$ $13$ являются началом знаменитой последовательности чисел Фибоначчи
$ \{1,$ $1,$ $2,$ $3,$ $5,$ $8,$ $13,$ $21,$ $34,$ $55,$ $89,\ \dotso\}.$
Эта последовательность задаётся рекуррентным соотношением $$ F_n=F_{n-1}+F_{n-2} $$ и парой начальных чисел $F_0=1$, $F_1=1$.
Между числами Фибоначчи существует много интересных соотношений. В $1680$ году французский астроном итальянского происхождения Джованни Доминико Кассини, открывший спутники Сатурна и щель в его кольцах, заметил такое соотношение: $F_{n+1}\cdot F_{n-1}-F_n^2=(-1)^n$, которое теперь называют его именем.
При $n=6$ получается равенство $5\cdot 13-8^2=1$ — знакомые по «Парадоксу шахматной доски» числа и знакомое увеличение на единицу! А вот принять за сторону квадрата число Фибоначчи с нечётным номером нельзя — детали в соответствующий прямоугольник можно сложить только с наложением (в пересечении — всё тот же параллелограмм единичной площади).
В «треугольнике Гарднера» катеты маленьких (настоящих и не меняющих площадь) треугольников являются числами Фибоначчи: у красного — 3 и 8, у жёлтого — 2 и 5. Соответственно стороны прямоугольника (в котором и происходит увеличение на клетку) получаются: до перекладки — 3 и 5, а после перекладки — 2 и 8. Увеличение площади прямоугольника на клетку обеспечивает соотношение на четыре последовательных числа Фибоначчи: $F_{n}\cdot F_{n-3}-F_{n-1}\cdot F_{n-2}=(-1)^n$, которое можно получить из соотношения Кассини и рекуррентного соотношения. Для $n=6$ получается равенство $8\cdot 2-5\cdot 3=1$, на котором основан «треугольник Гарднера».
Таким образом, софизмы построены на том, что размеры фигур и частей, из которых они составляются, суть нескольких подряд идущих числах Фибоначчи. Опираясь на эти соотношения можно построить аналогичные софизмы и для фигур больших размеров. В варианте Лойда надо не забывать про чётность, а в варианте Гарднера — если желать, чтобы площадь собиралась в квадратную клетку, придётся увеличивать количество частей, из которых составлен основной прямоугольник.
Для чисел Фибоначчи существует и явное, а не рекуррентное, задание, называемое формулой Бине $$ F_n=\frac{1}{\sqrt{5}}\Big(\frac{1+\sqrt{5}}{2}\Big)^n-\frac{1}{\sqrt{5}}\Big(\frac{1-\sqrt{5}}{2}\Big)^n. $$ Отметим, что хотя числа Фибоначчи целые, в формуле для них возникает число иррациональное — золотое сечение $\phi=\dfrac{1+\sqrt5}2$.
Первая скобка в формуле Бине равна примерно $1{,}618$, а вторая скобка — число отрицательное и по модулю меньшее единицы (примерно $-0{,}618$). Значит, числа Фибоначчи быстро растут, а точнее, $F_n\sim\dfrac1{\sqrt5}\varphi^n$. Это объясняет, почему с ростом $n$ щель в виде параллелограмма становится всё уже и обман всё сложнее заметить (сравните, например, маленький и большой «треугольники Гарднера»). Действительно, наклоны разных отрезков в софизмах имеют вид $\dfrac{F_{n+2}}{F_n}$, а с ростом $n$ эти отношения становятся всё ближе к $\phi^2$ и практически неразличимы.
Появившийся единичный параллелограмм и его диагональ являются объектами красивой науки, начала которой заложил Герман Минковский, — геометрии чисел. Более точно — геометрической интерпретации цепных дробей.
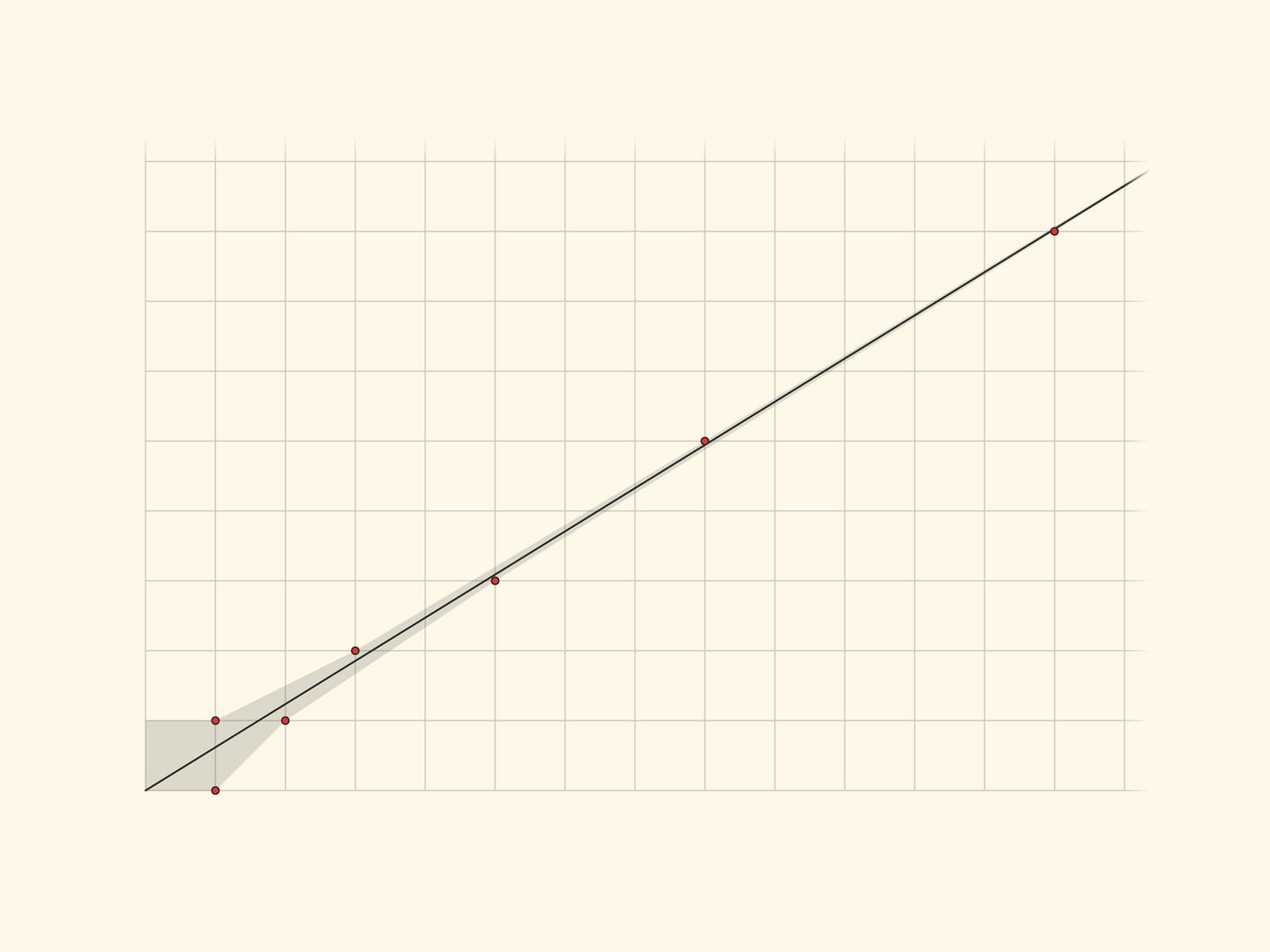
На рисунке показана прямая $x=\dfrac{1+\sqrt{5}}2y$ и отмечены наиболее близкие к ней узлы сетки. Их координаты — соседние числа Фибоначчи, а сами точки, прыгая поочерёдно то выше прямой, то ниже, приближаются к ней. А отношения соседних чисел Фибоначчи дают в некотором смысле наилучшие рациональные приближения золотого сечения… Заинтригованному читателю советуем брошюру Владимира Игоревича Арнольда «Цепные дроби».
Казалось бы, просто фокус, просто картинки, ходящие в интернете… А сколько нетривиальной математики в них заложено!
Литература
Игнатьев Е. И. В царстве смекалки или арифметика для всех: книга для семьи и школы. Книга вторая. — Санкт-Петербург, 1909. — [Раздел «Геометрические софизмы»]. — [Следует смотреть издания 1908—1924 годов — они существенно полнее и содержательнее последующих].
Кордемский Б. А. Математическая смекалка. — М.: ГТТЛ, 1954. — [Глава 14 «Числа древние, но вечно юные», Б. «Числа Фибоначчи»].
Sillke T. Geometrical Paradox. — [Стоит обратить внимание на обширный список литературы].
Спивак А. В. Числа Фибоначчи // Новая школьная энциклопедия. Т. «Небесные тела. Числа и фигуры». — М.: Росмэн-пресс, Мир книги, 2005. — Стр. 396—401. — [Переиздание: «Математика: полная энциклопедия». — М.: Росмэн-пресс, 2020].
Воробьёв Н. Н. Числа Фибоначчи. — 4‐е изд., доп. — М.: Наука, 1978. — (Популярные лекции по математике; Вып. 6).
Грэхем Р., Кнут Д., Паташник О. Конкретная математика: Основание информатики. — М.: Мир, 1998. — [2‐e изд.: М.: Мир, Бином, 2009]. — [§ 6.6 «Числа Фибоначчи»].
Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — [Глава 11 «Золотое сечение и филлотаксис», стр. 236—252].
Арнольд В. И. Цепные дроби. — М.: МЦНМО, 2009. — (Библиотека «Математическое просвещение»; Вып. 14).
Филлотаксис // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 78, 318.