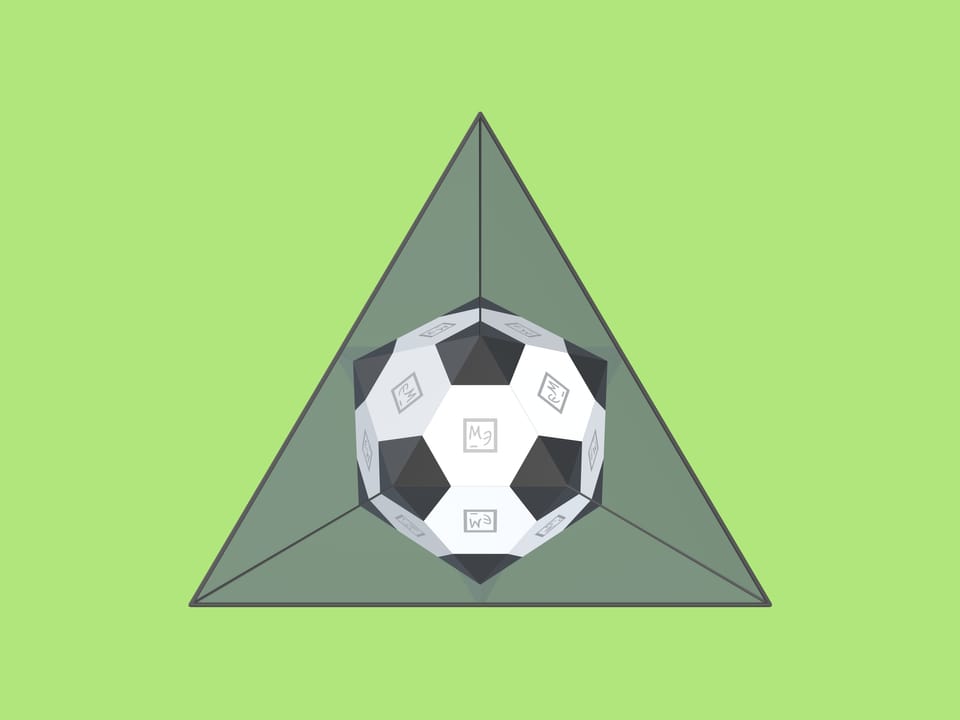
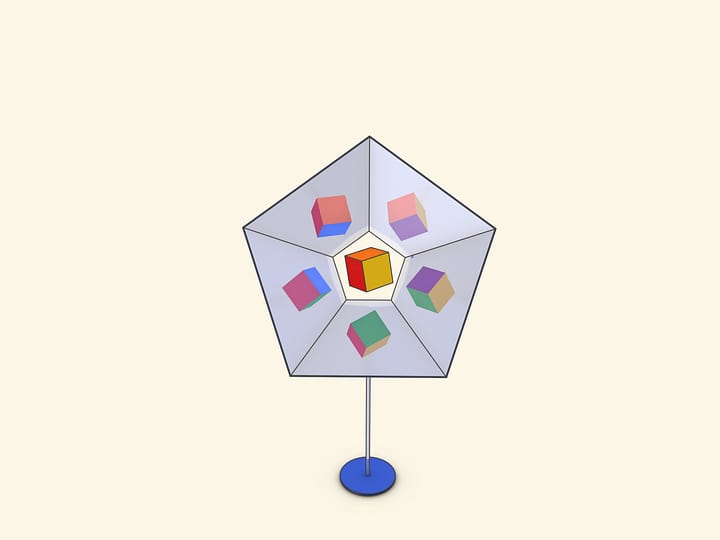
Поверхность классического футбольного мяча состоит из «слегка искривлённых» 12 правильных пятиугольников чёрного цвета и 20 правильных белых шестиугольников.
Кстати, «классическим» такой мяч был не всегда: впервые такие покрой и раскраска были использованы для официального мяча на чемпионате мира в 1970 году в Мексике. Чёрно-белая раскраска тогда была выбрана из соображений контрастности, чтобы мяч был лучше виден на преобладавших в то время чёрно-белых телевизорах. Да и само название — Telstar — он получил в честь телевизионного спутника. В последующие годы раскраска официальных мячей менялась, но покрой оставался неизменным вплоть до чемпионата 2002 года.
С точки зрения математики, классический футбольный мяч является усечённым икосаэдром. Этот факт и теория групп, порождённых отражениями (в трёхмерном случае — многогранников Кокстера), позволяет сделать простую в изготовлении, но красивую модель.
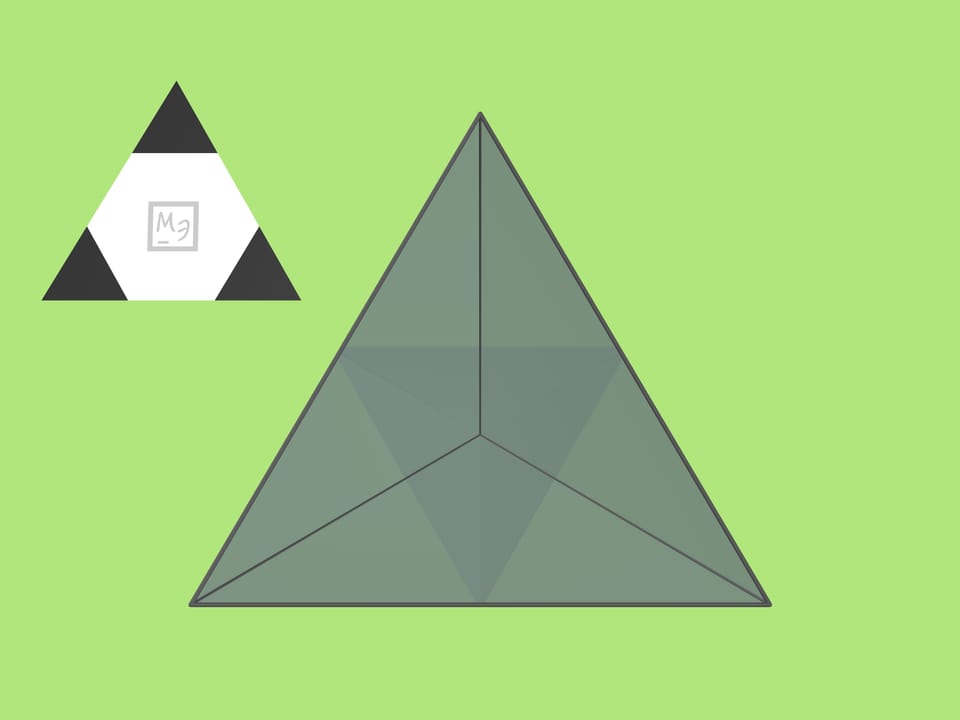
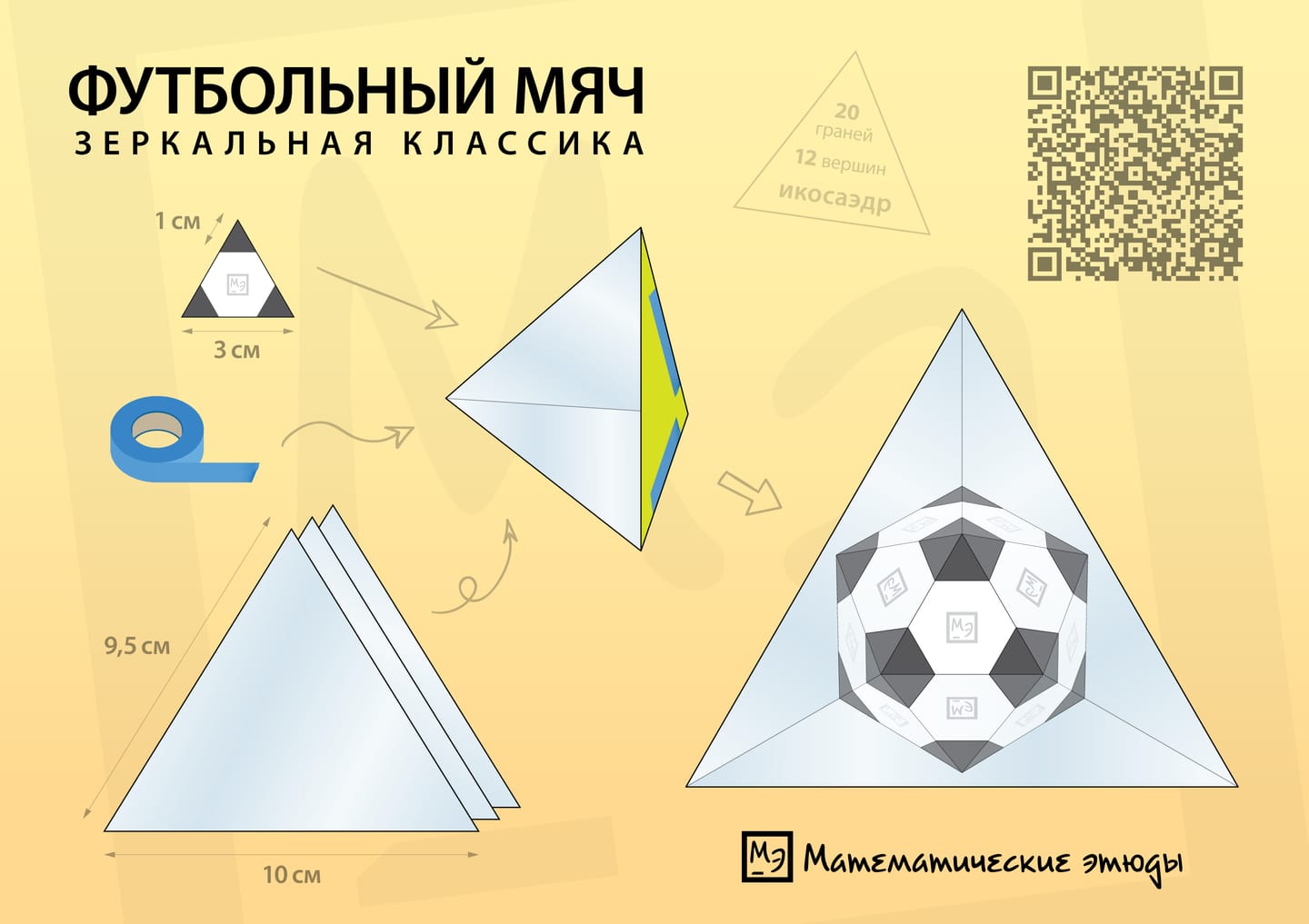
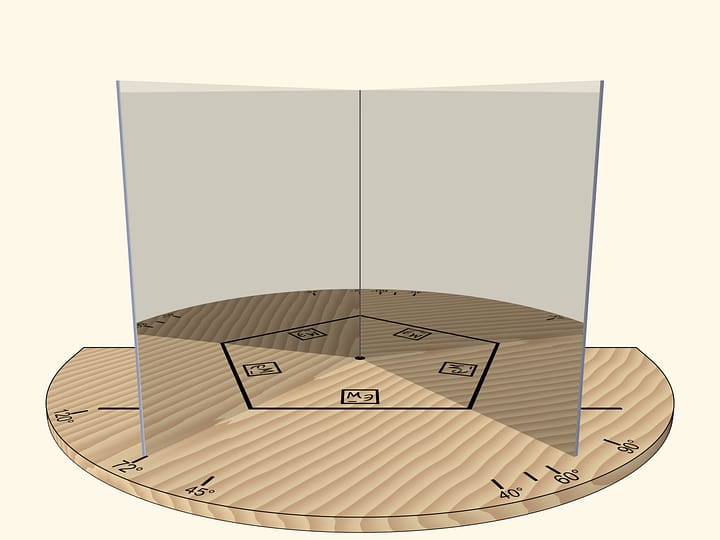
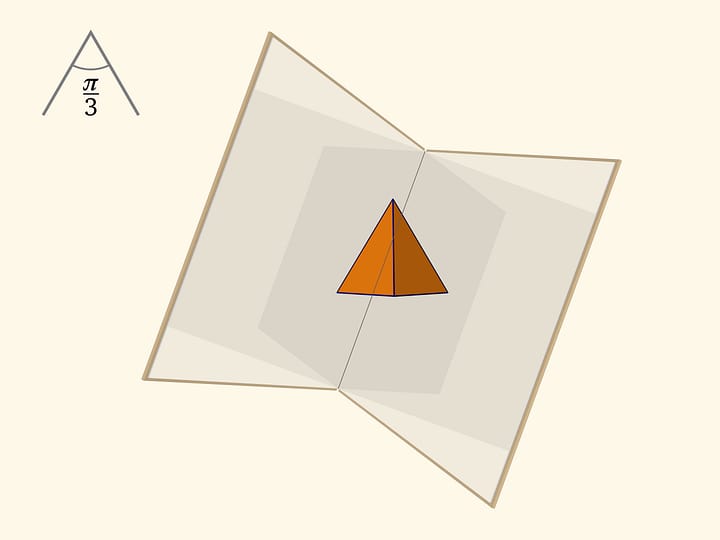
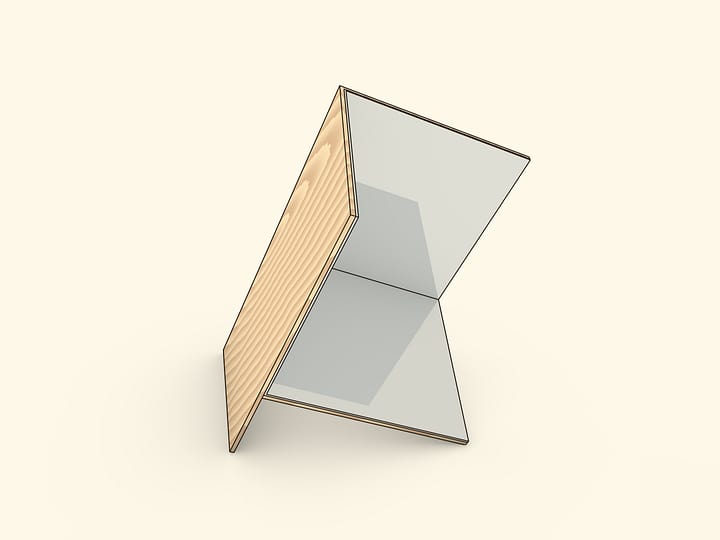
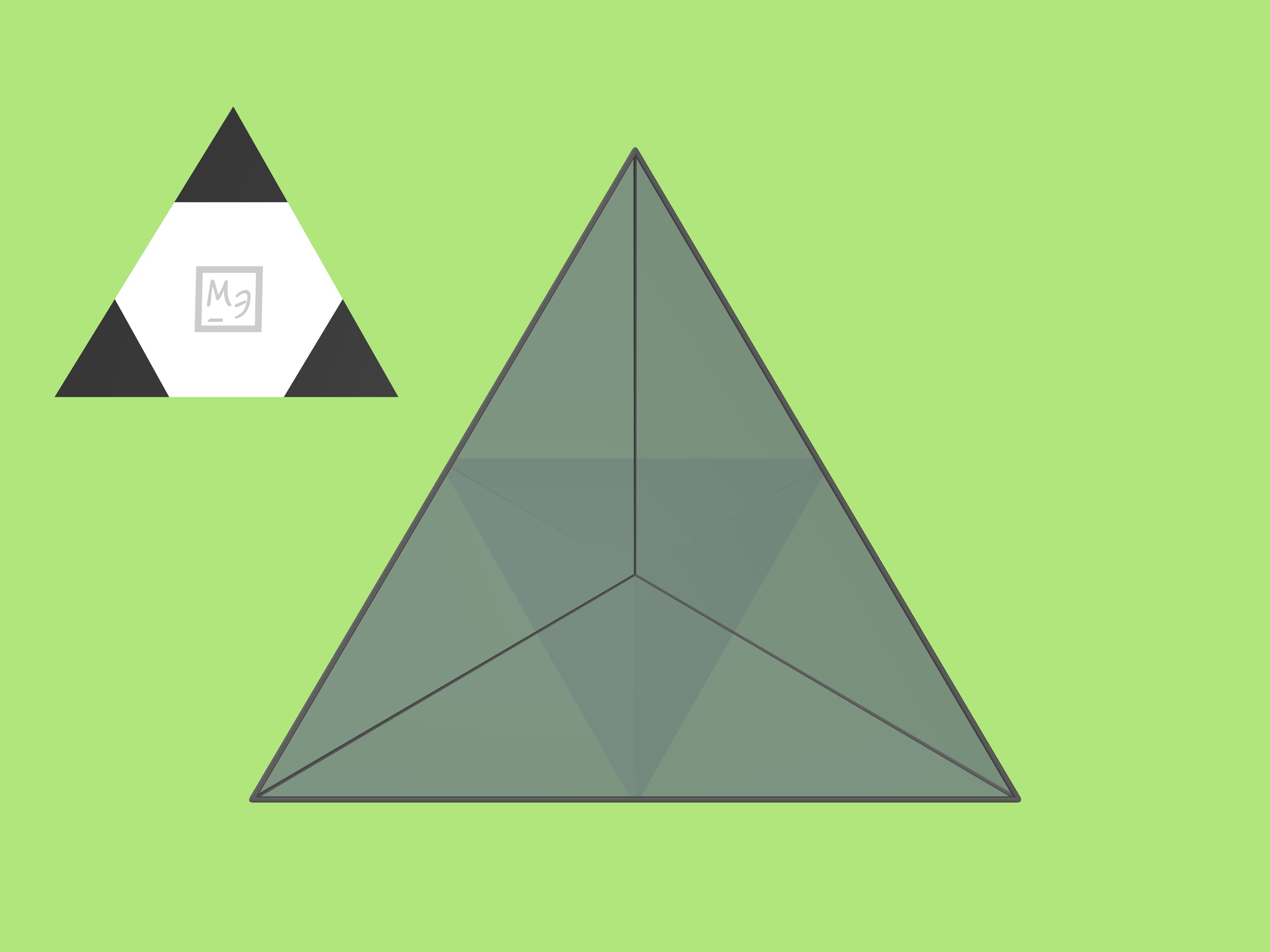
Следует взять зеркальный трёхгранный угол, составленный из одинаковых равнобедренных треугольников. При длине основания $a$ боковые стороны, по которым склеиваются треугольники в угол, должны иметь длину $r=\frac{1}{4}\sqrt{2(5+\sqrt{5})}\,a$ или с хорошей точностью $r\approx0{,}95\,a$. (Например, если взять $a=10$ см, то $r=9{,}5$ см.) Зеркальный угол очень близок к правильному тетраэдру, но всё же отличается от него.
Ещё одна необходимая деталь — (плоский) правильный треугольник, окрашенный в белый и чёрный цвета так, что внутренняя белая область является правильным шестиугольником. (Для этого стороны чёрных треугольников надо взять в три раза меньше стороны исходного правильного треугольника.)
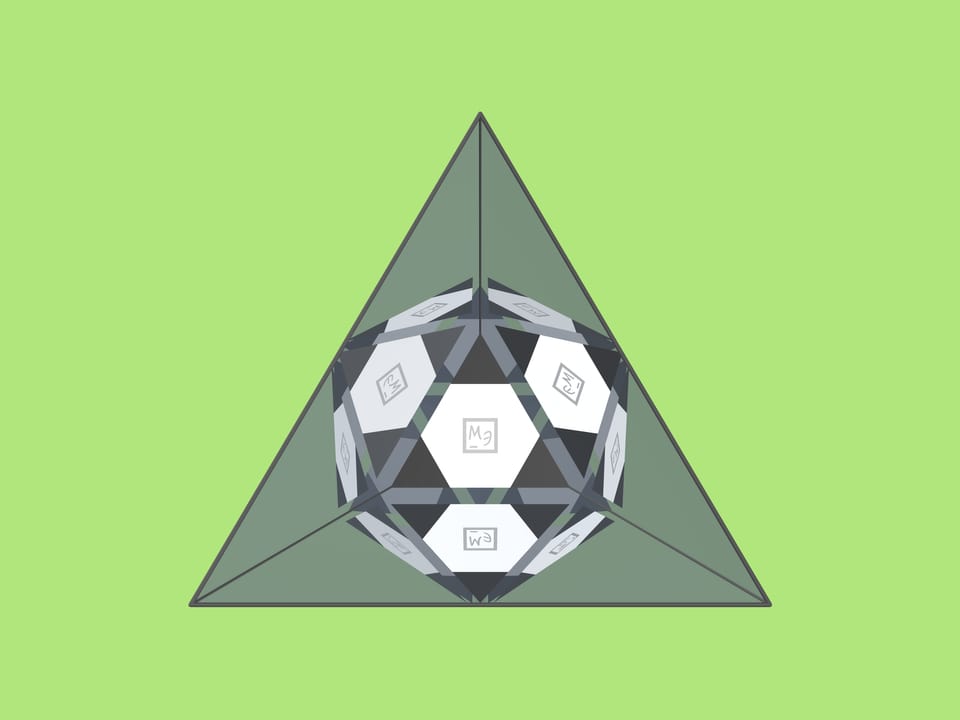
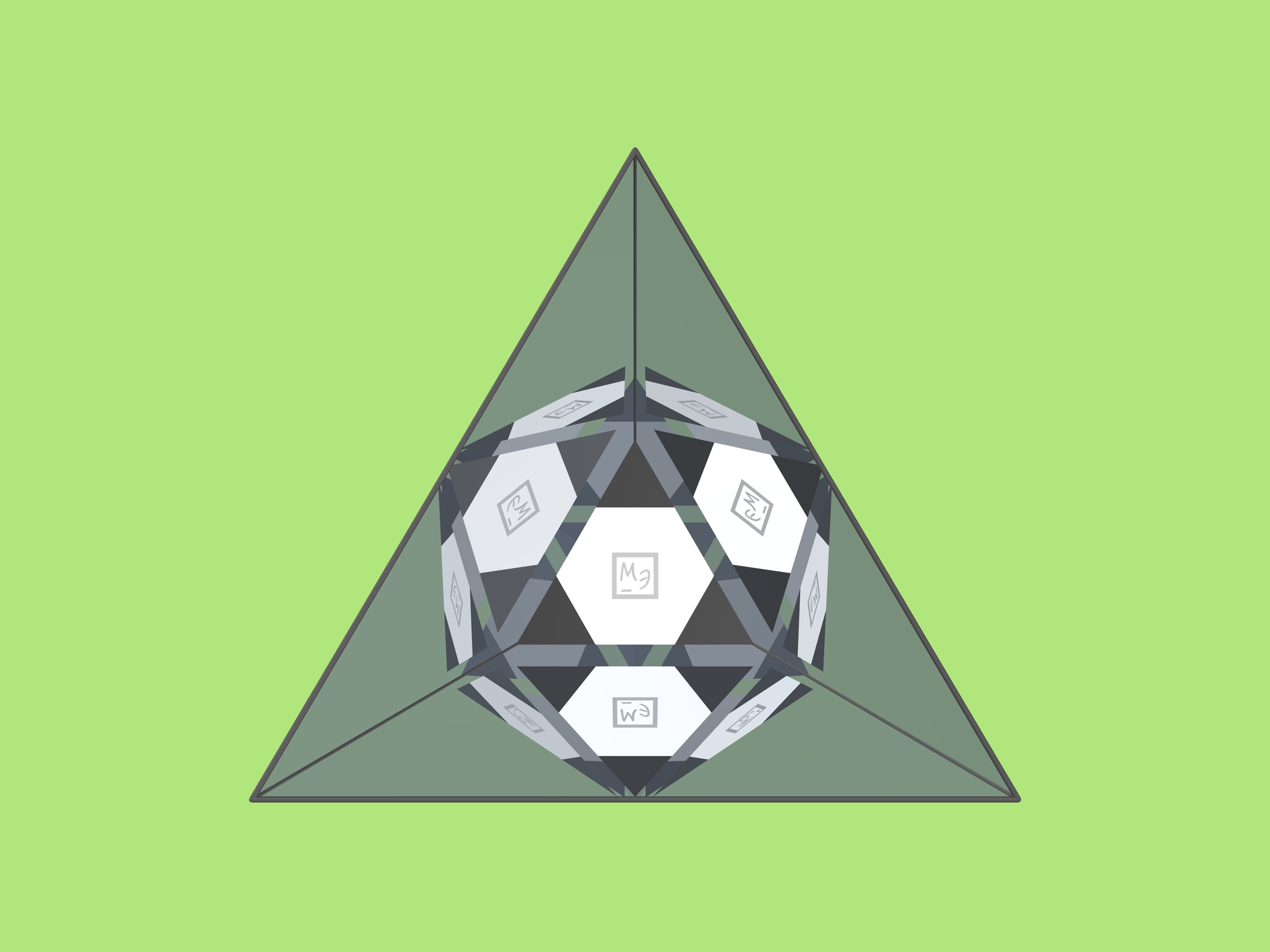
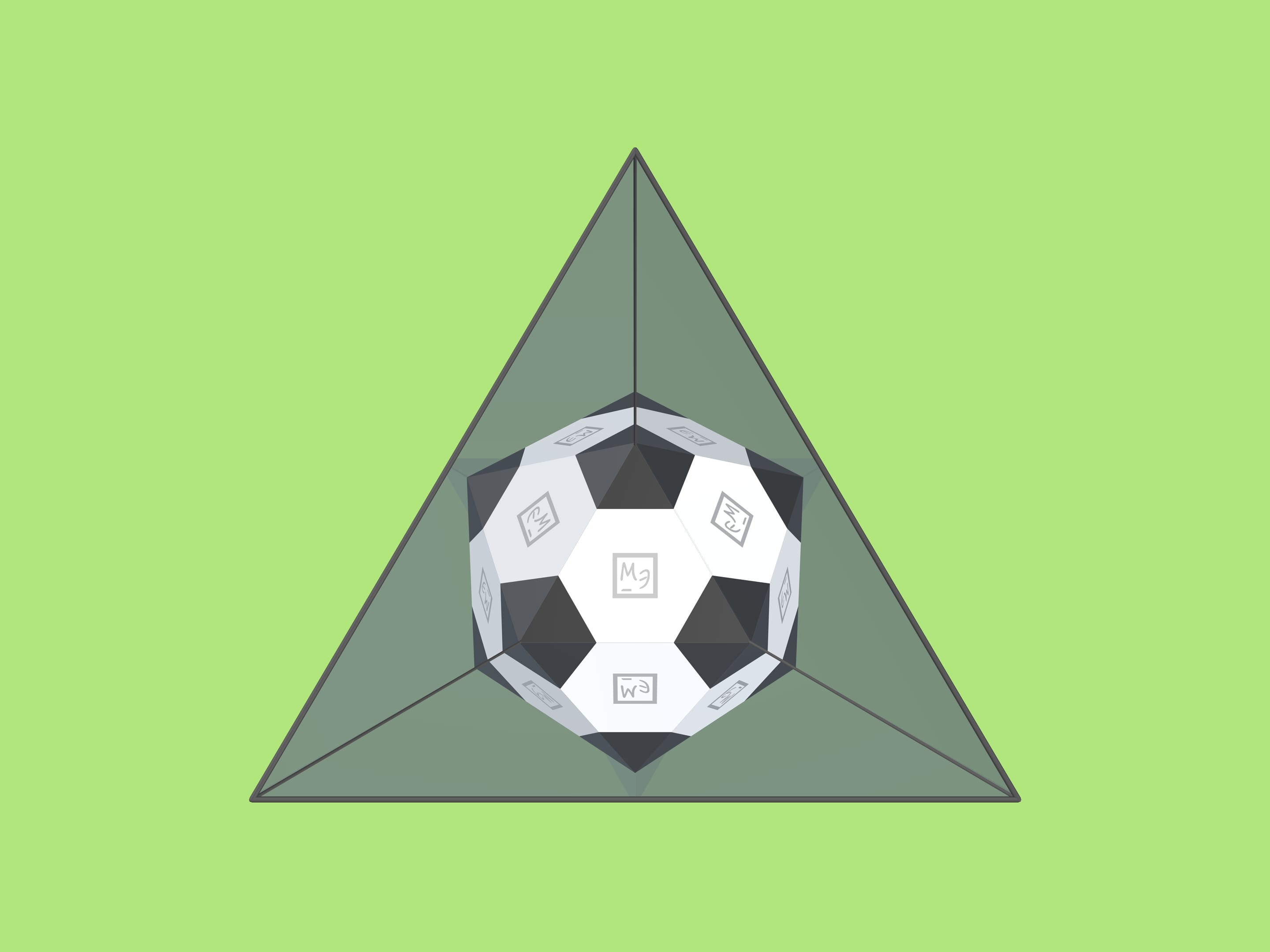
Если такой треугольник вложить в трёхгранный угол, вы увидите модель классического футбольного мяча! При покачивании угла относительно оси зрения картинка меняться не будет.
Чтобы при отражении «мяч» был виден полностью, вкладываемый треугольник не должен быть слишком большим. Вкладывать его надо не дальше чем на треть высоты от вершины зеркального угла. (Значит, при основании зеркального треугольника $a=10$ см длину стороны вкладываемого треугольника можно сделать равной $3$ см, соответственно стороны маленьких чёрных треугольников на нём — по $1$ см.)
Зеркальные равнобедренные треугольники проще всего вырезать из пластика с зеркальным напылением. А скрепить их можно с помощью скотча или широкой изоленты, склеив вдоль боковых сторон — рёбер трёхгранного угла.
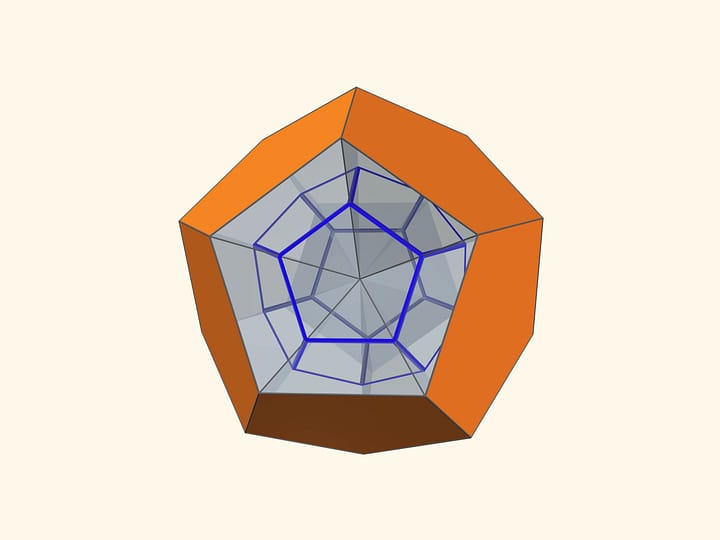
Что же это за такой магический зеркальный угол, в котором при отражениях виден футбольный мяч? (А на самом деле — икосаэдр, который виден ещё более явно, если вложить одноцветный треугольник.)
Зеркальный угол связан с самим икосаэдром: его вершина расположена в центре икосаэдра, а зеркала проходят через стороны одной из граней икосаэдра. Отсюда получаются и условия на стороны равнобедренных треугольников, образующих зеркальный угол: если основание треугольника $a$ — длина ребра икосаэдра, то боковая сторона $r$ — радиус описанной около икосаэдра сферы.
А то, что картинка в таком зеркальном угле будет икосаэдром, гарантирует теория групп, порождённых отражениями.
Литература
Футбольный мяч // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 154—155, 344-345.