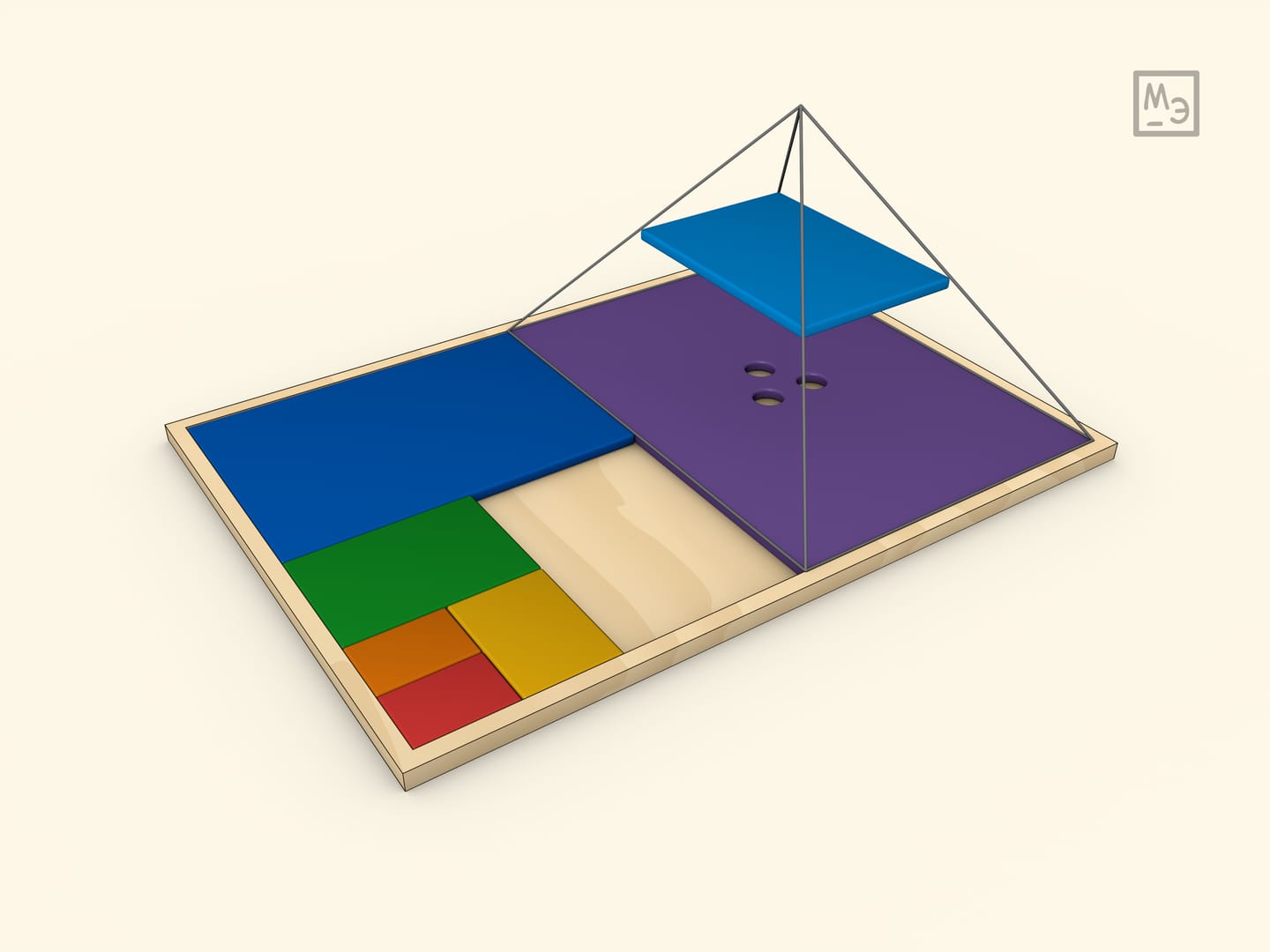
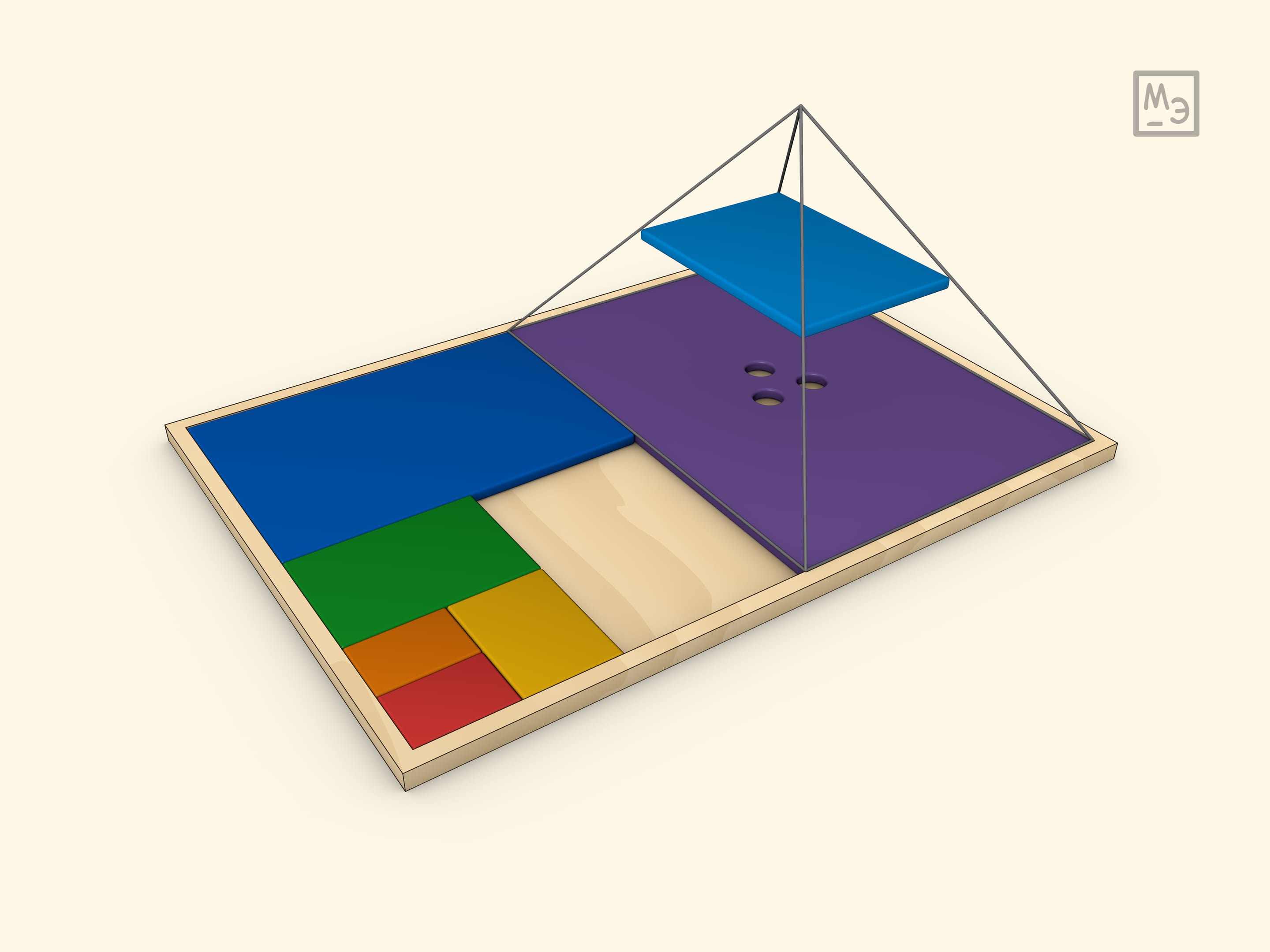
Сумма бесконечной геометрической прогрессии⁠

Сумма бес­ко­неч­ной геомет­ри­че­ской прогрес­сии равна $b_1/(1-q)$, где $b_1$ — пер­вый член прогрес­сии, а $q$ — её знаме­на­тель ($|q|<1$). В случае $q=1/2$ сумму можно «вычислить» геометрически.

Если при­нять площадь большей детали за 1, то сумма площа­дей всех дета­лей оче­видно равна 2.

Если поле сде­лать не про­из­воль­ным, а с отноше­нием сто­рон рав­ным $\sqrt{2}$, то все полу­чающи­еся при деле­нии попо­лам детали будут подобны друг другу.

Модель можно сде­лать из дерева или кар­тона. Для учащихся сред­них клас­сов она может служить иллю­страцией и как суммы бес­ко­неч­ной геомет­ри­че­ской прогрес­сии со знаме­на­те­лем $1/2$, и как суммы степе­ней двойки. А для учащихся млад­ших клас­сов — голо­во­лом­кой.