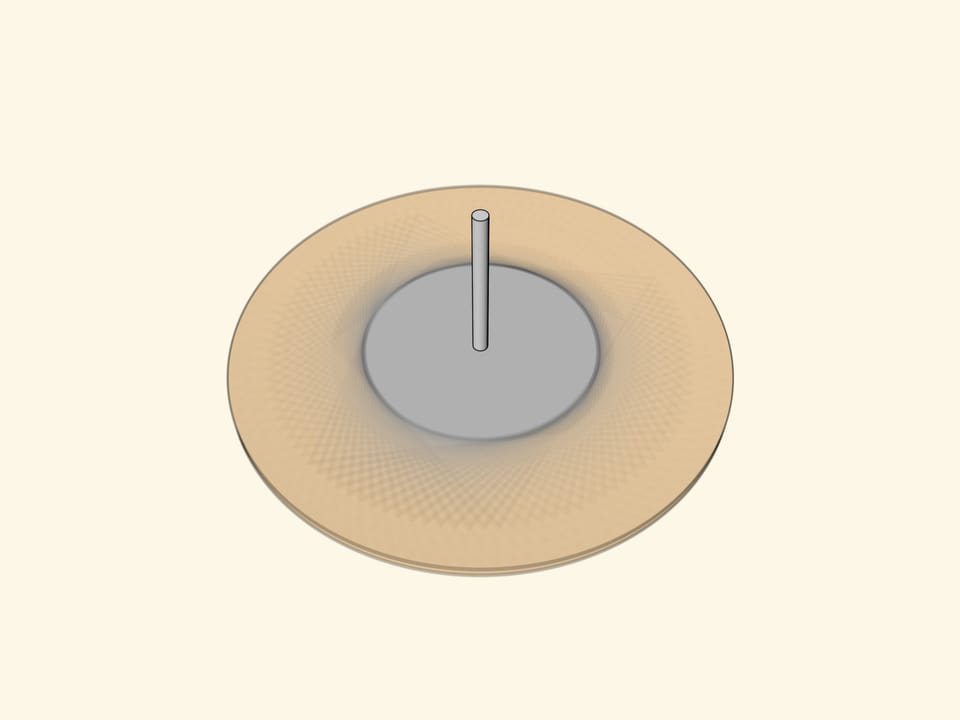
Простейший волчок поможет увидеть даже не нарисованную вписанную в треугольник окружность.
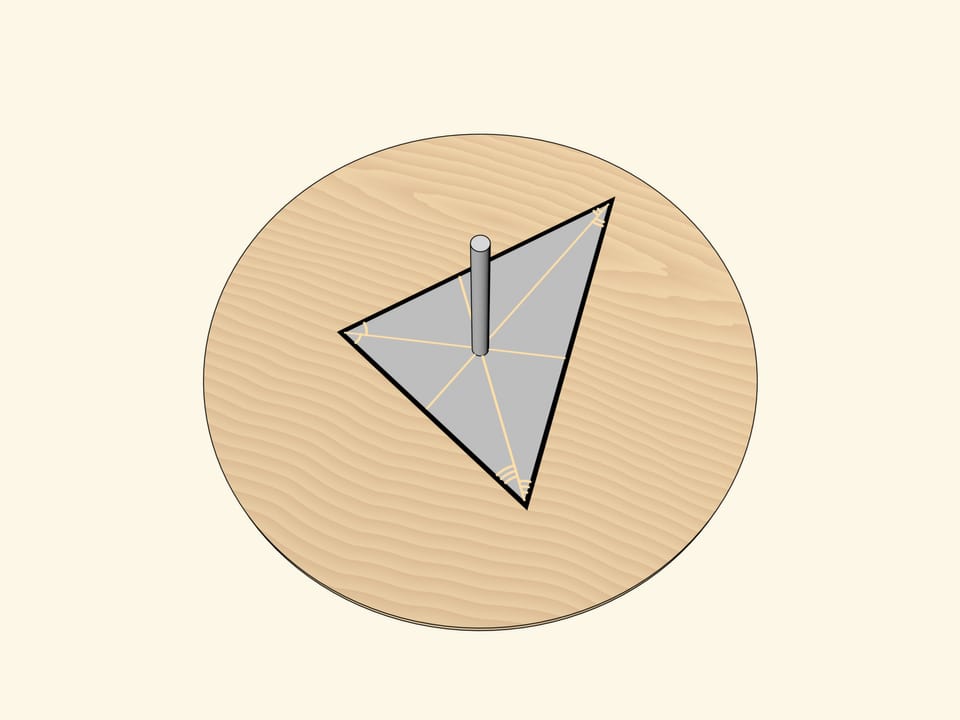
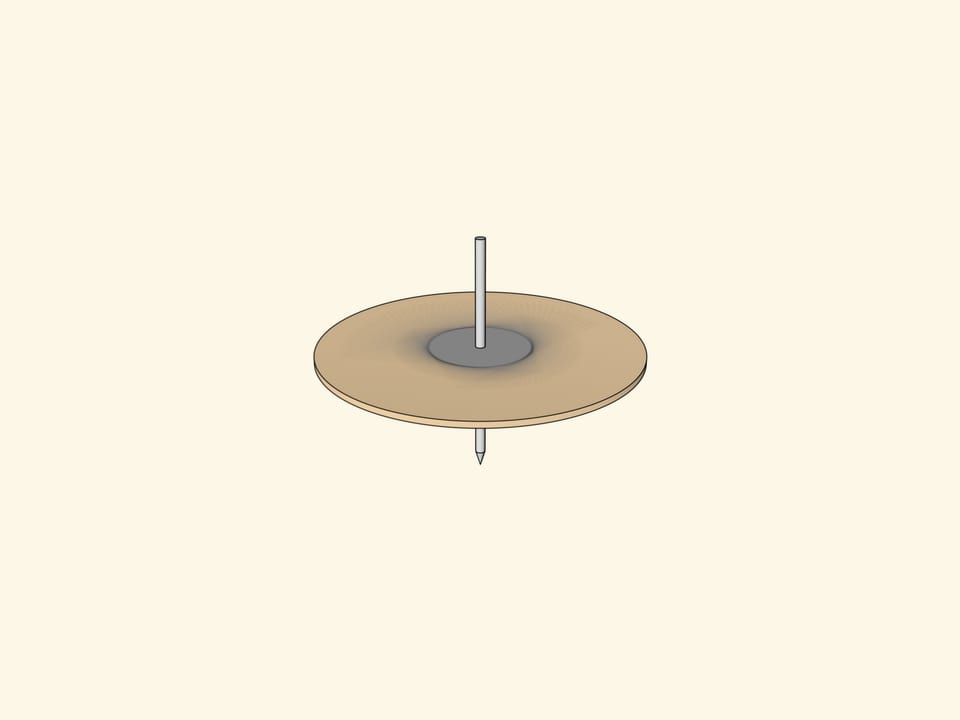
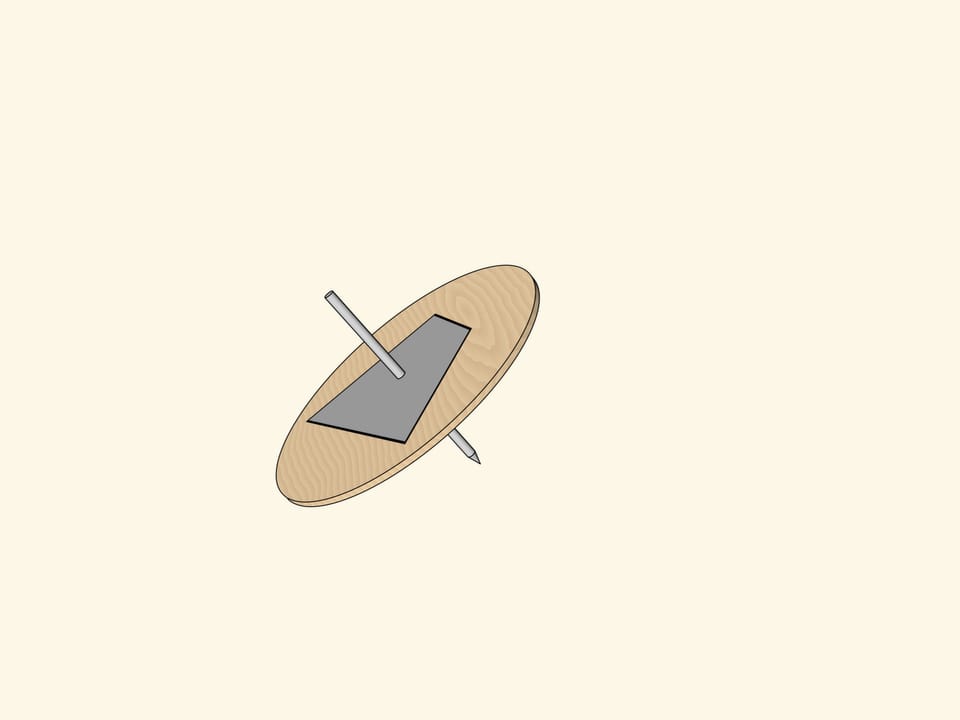
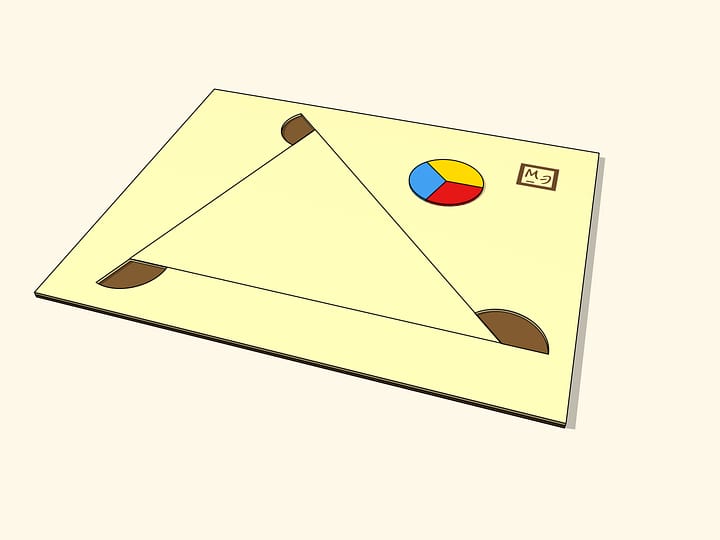
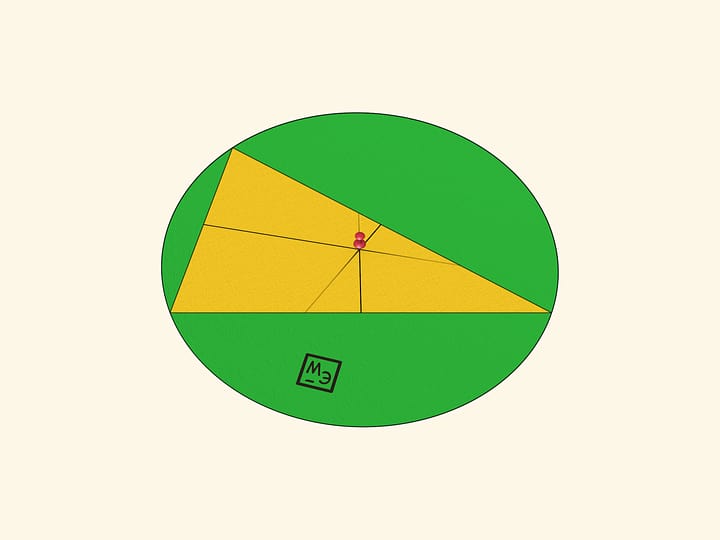
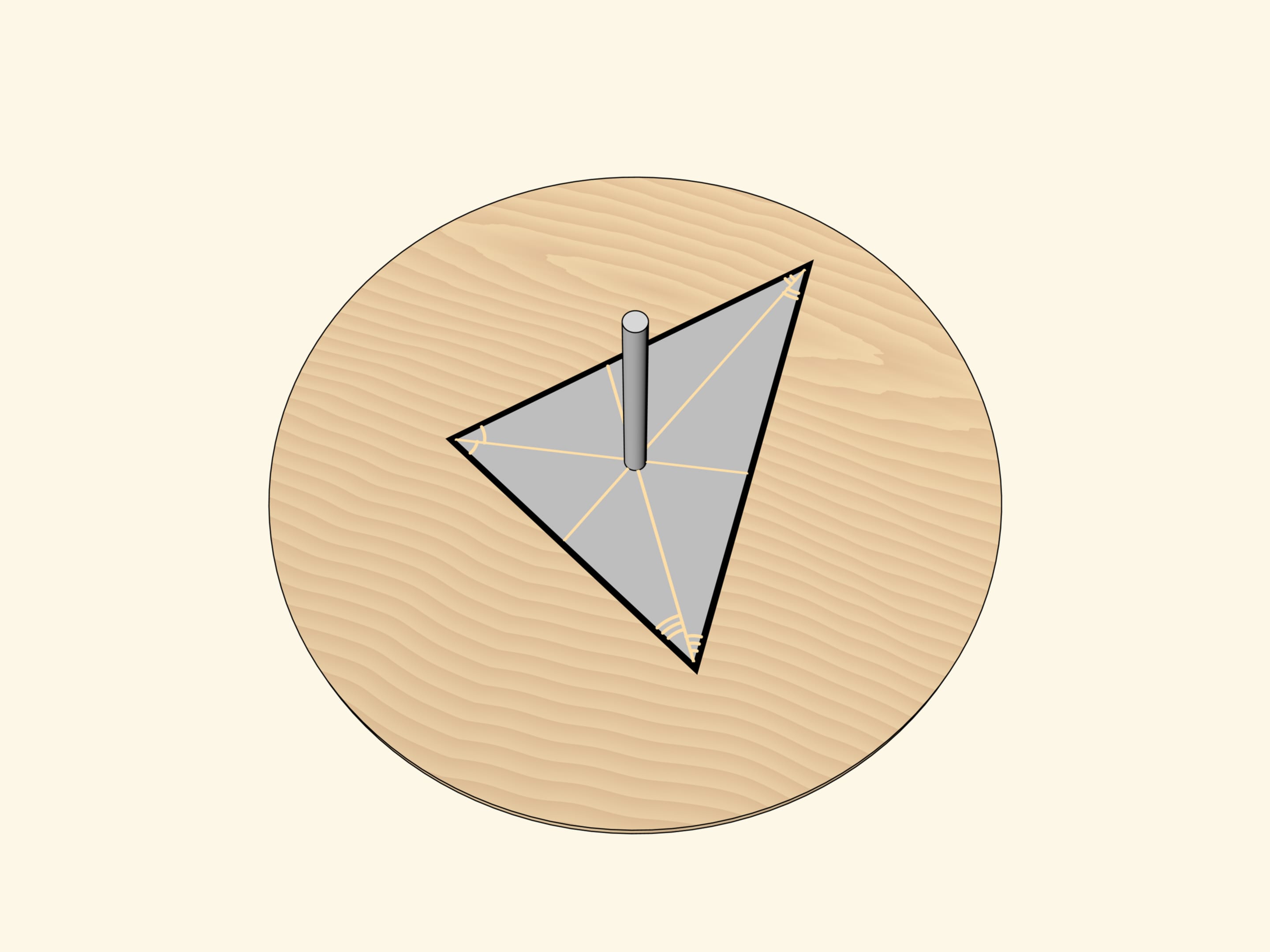
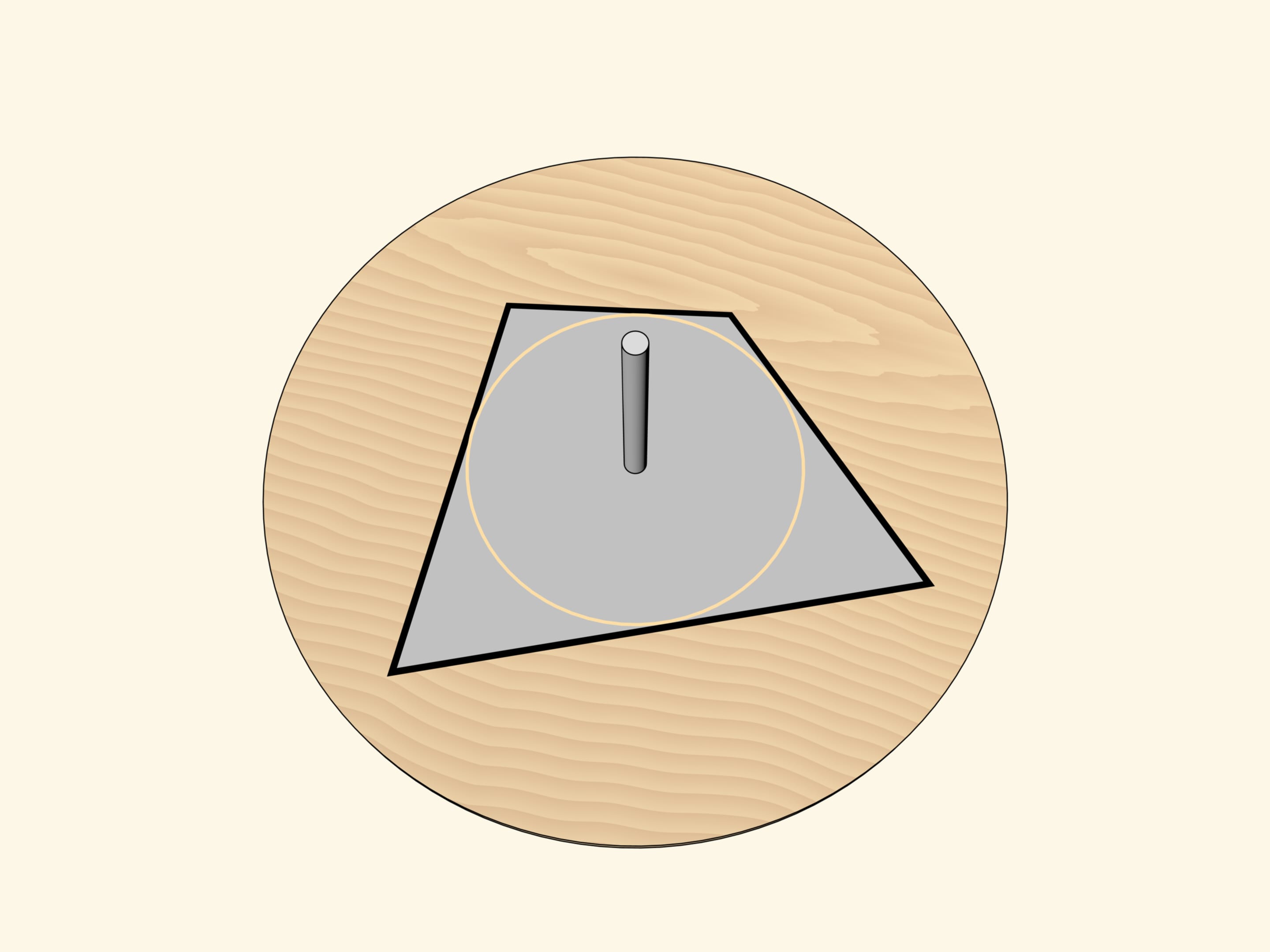
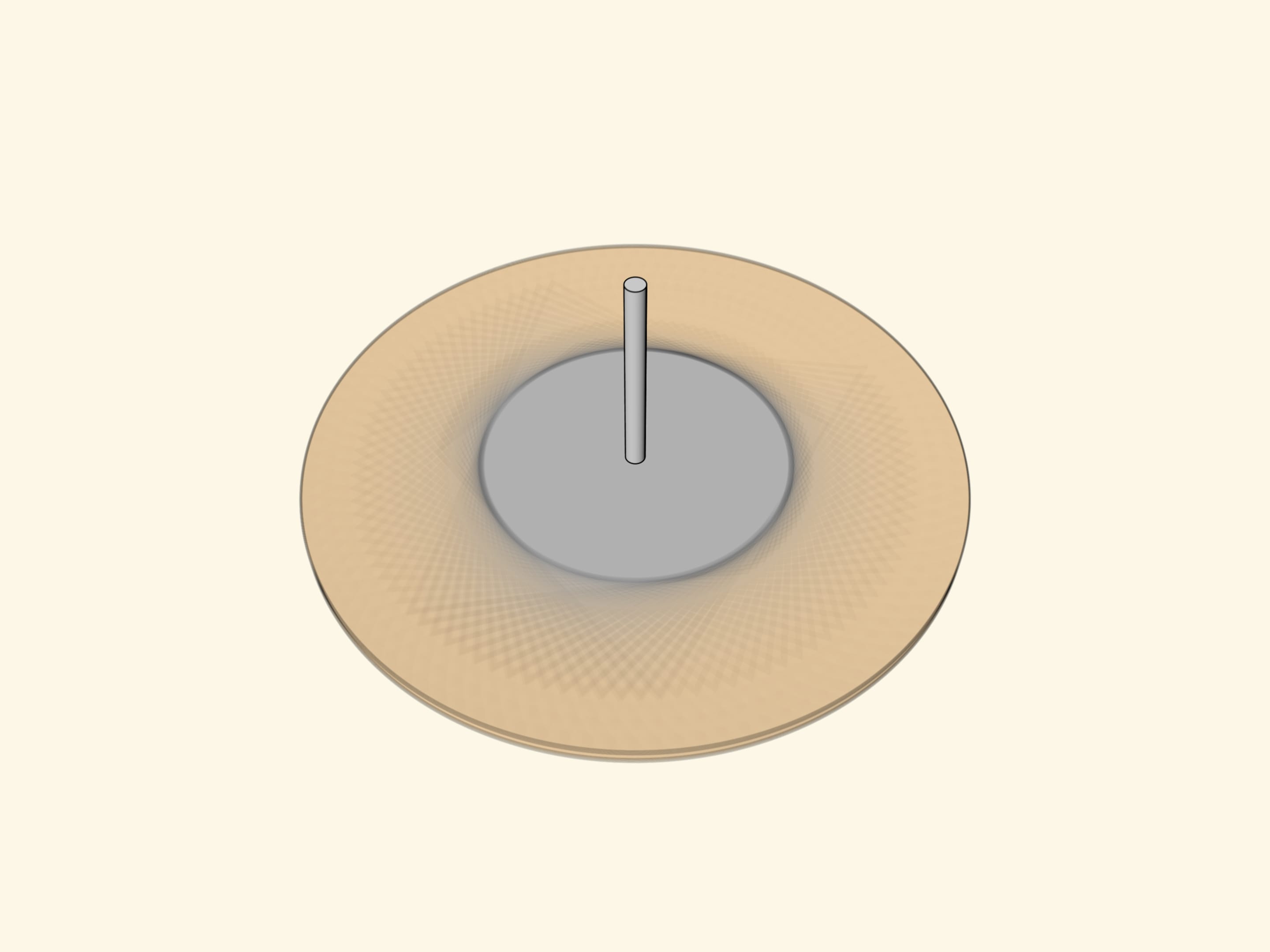
На плоской поверхности волчка следует нарисовать треугольник так, чтобы ось волчка проходила через точку пересечения биссектрис треугольника. Если раскрутить волчок, то мы увидим… вписанную в треугольник окружность. Не треугольник, который нарисован, а не нарисованную (!) окружность, вписанную в треугольник.
Дело в том, что при вращении треугольника вокруг точки пересечения биссектрис вписанная окружность является огибающей всевозможных положений сторон треугольника. Внутрь окружности стороны «не заходят». А вдоль окружности при ненулевой толщине сторон треугольника закрашенные точки сливаются для глаза в окружность.
В случае произвольного выпуклого многоугольника с большим числом вершин все биссектрисы внутренних углов могут не пересекаться в одной точке — в таком случае вписать окружность в такой многоугольник невозможно.
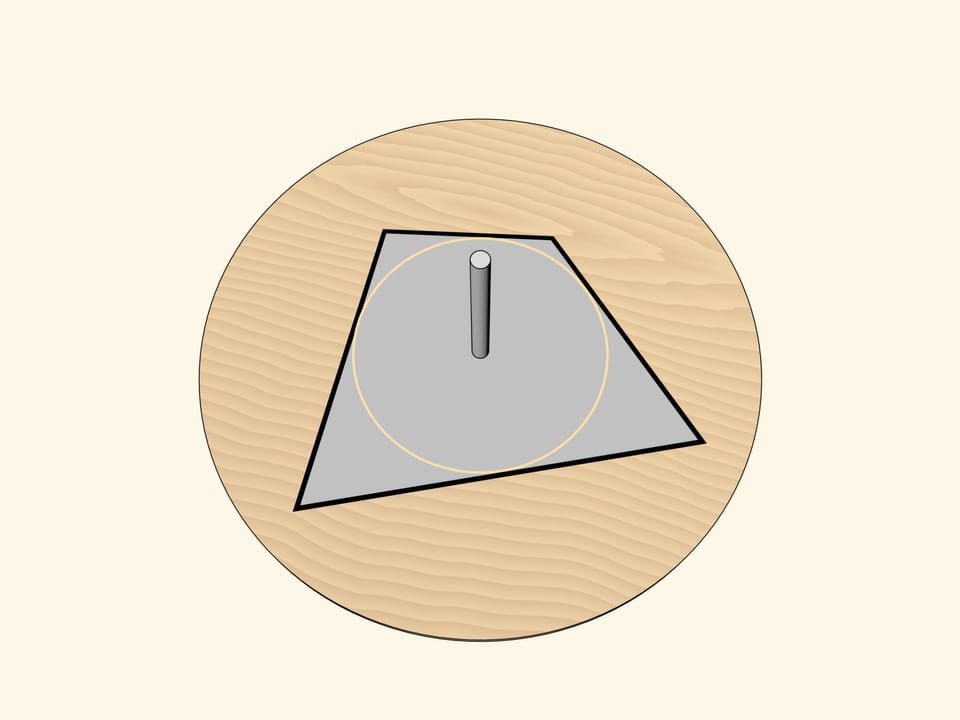
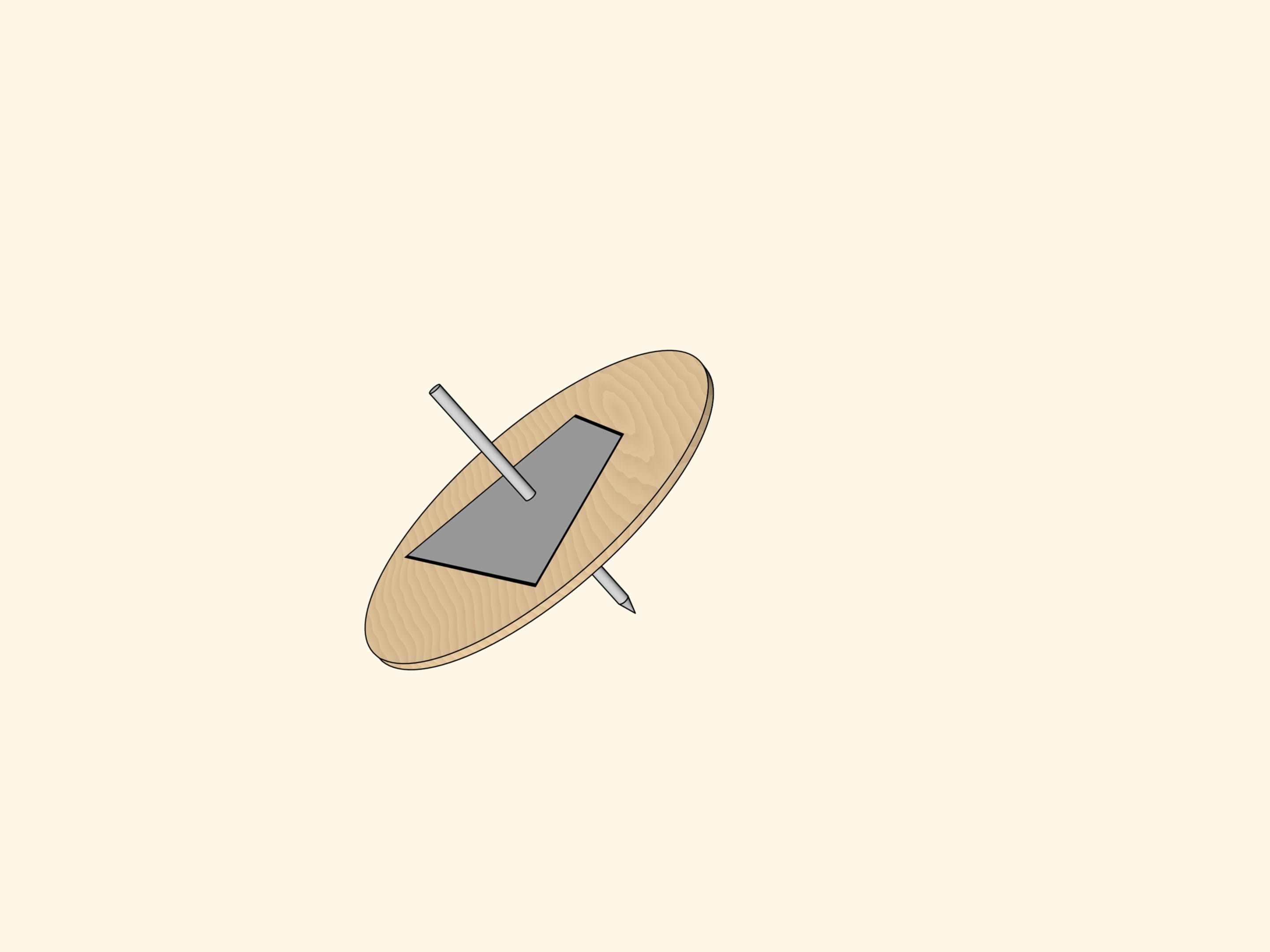
Но если выбрать многоугольник, например четырёхугольник, описанный около окружности, нарисовать его на поверхности волчка так, чтобы ось проходила через центр вписанной окружности, то эффект будет тот же. На крутящемся волчке будет виден не сам многоугольник, а его вписанная окружность.