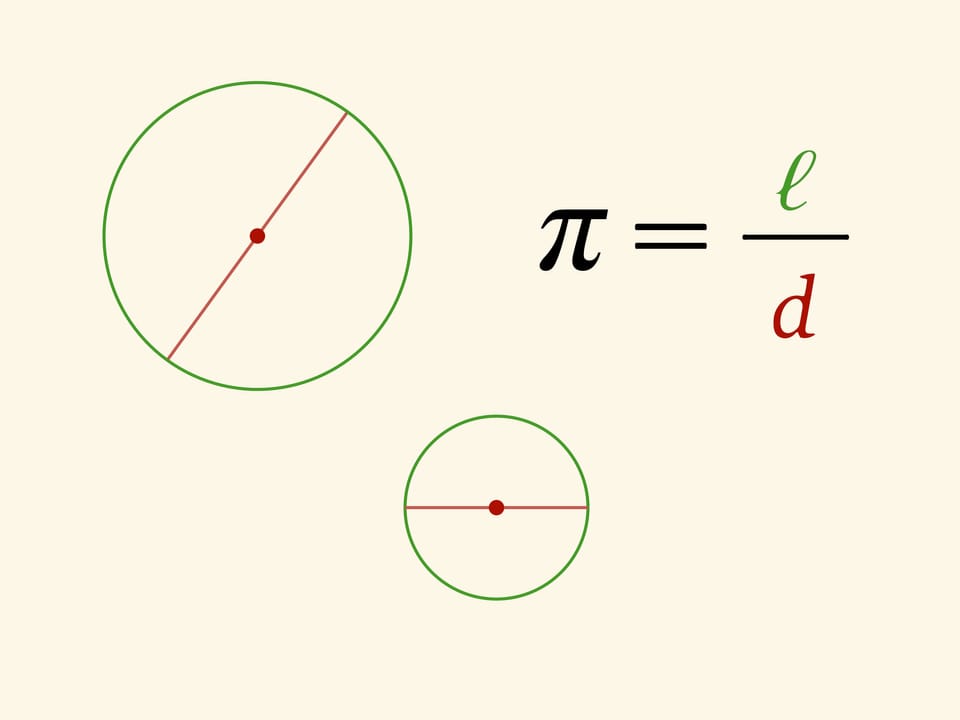Отношение длины окружности к диаметру не зависит от размера окружности, т. е. является фиксированным числом. Это число в математике обозначают буквой $\pi$.
Число $\pi$ представляется бесконечной непериодической десятичной дробью $$ \pi=3,1415926535… $$
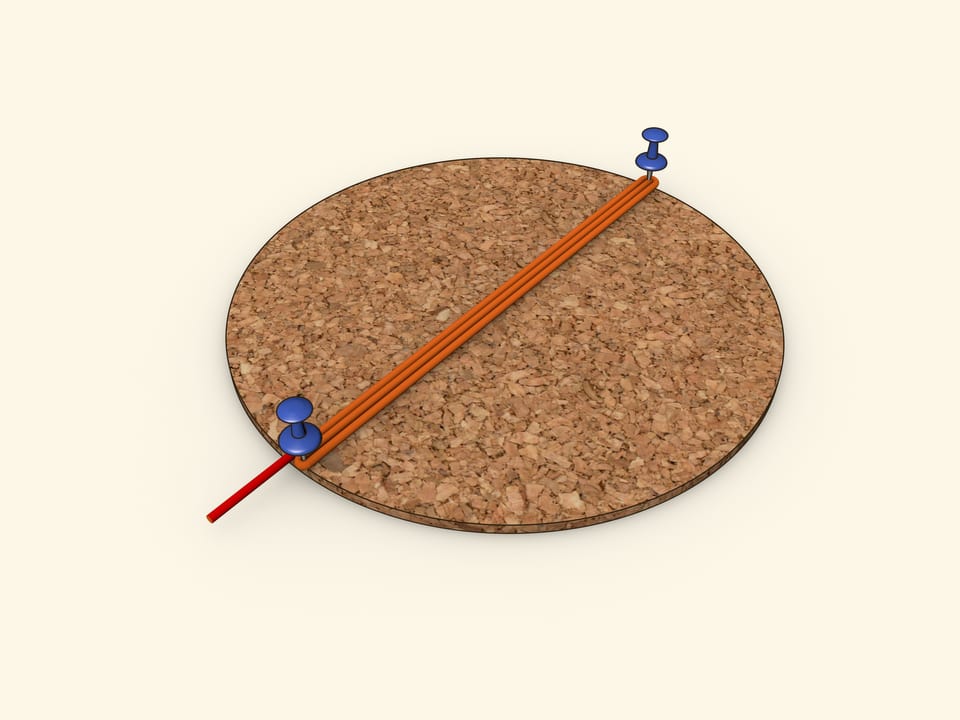
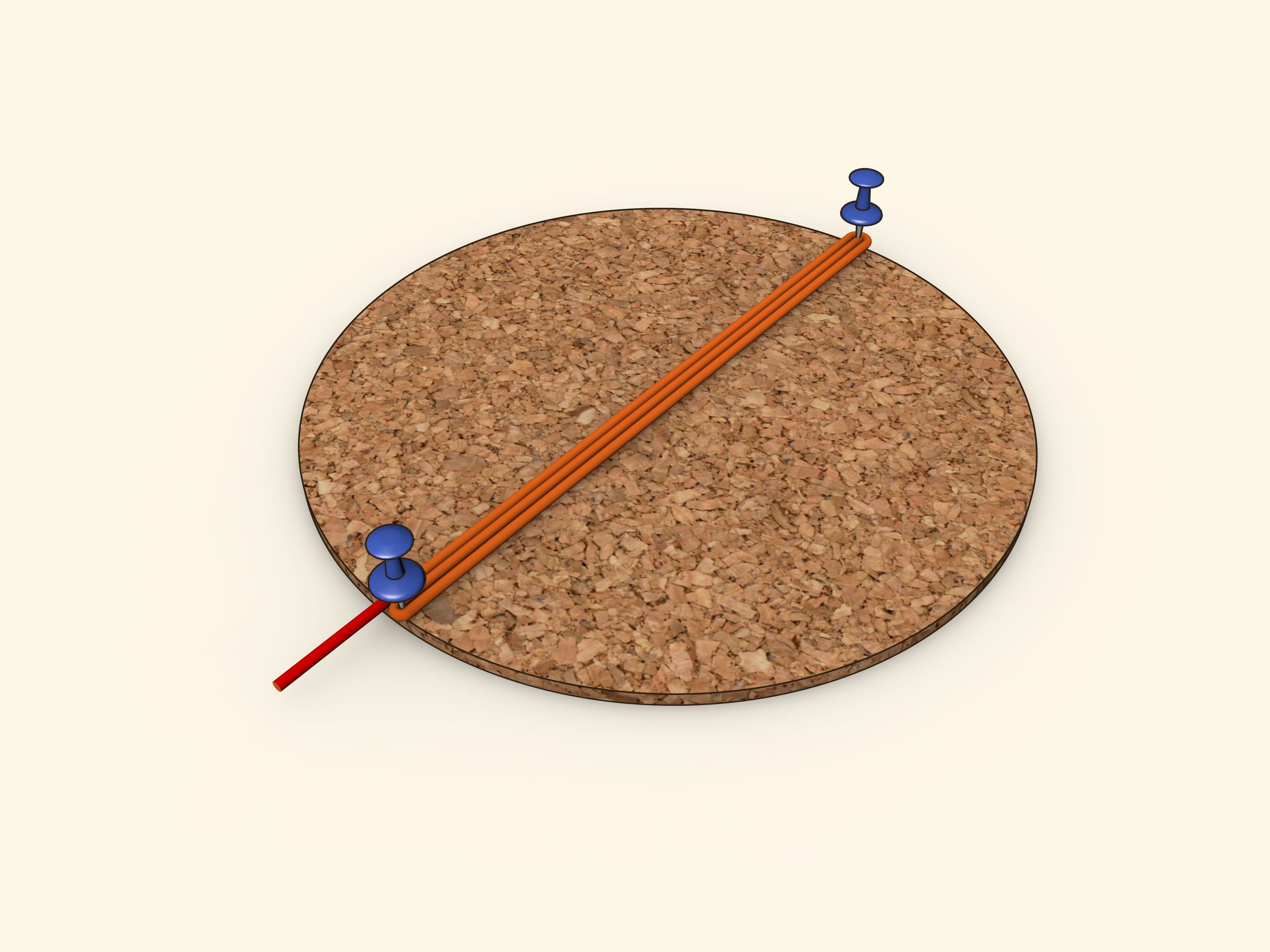
То, что $\pi$ равно «трём с хвостиком», можно продемонстрировать используя круглую пробковую подставку под горячее, верёвку и две кнопки.
Обмотаем лежащую на столе подставку и обрежем верёвку так, чтобы её длина была равна длине окружности.
Воткнув кнопки в диаметрально противоположные точки, можно показать, что та же самая верёвка три раза пройдёт вдоль диаметра круга и останется ещё «хвостик».
Борьба за максимально точное нахождение длины этого «хвостика» – была захватывающей и продолжалась столетиями.
Одним из свойств числа $\pi$ является то, что в его десятичной записи после запятой можно встретить дату вашего рождения.