Наиболее известная математическая задача упаковки — плотнейшая упаковка одинаковых шаров в пространстве (в двумерном случае — кругов на плоскости). В прикладном смысле интересно рассматривать задачи упаковки не во всё пространство, а в ограниченные объёмы. Постановки бывают разные, рассмотрим на плоскости такую: в какое минимальное по размеру поле заданной формы можно уложить $N$ одинаковых фигур? Известные решения этой задачи можно представить в виде головоломок. Приведём несколько примеров.
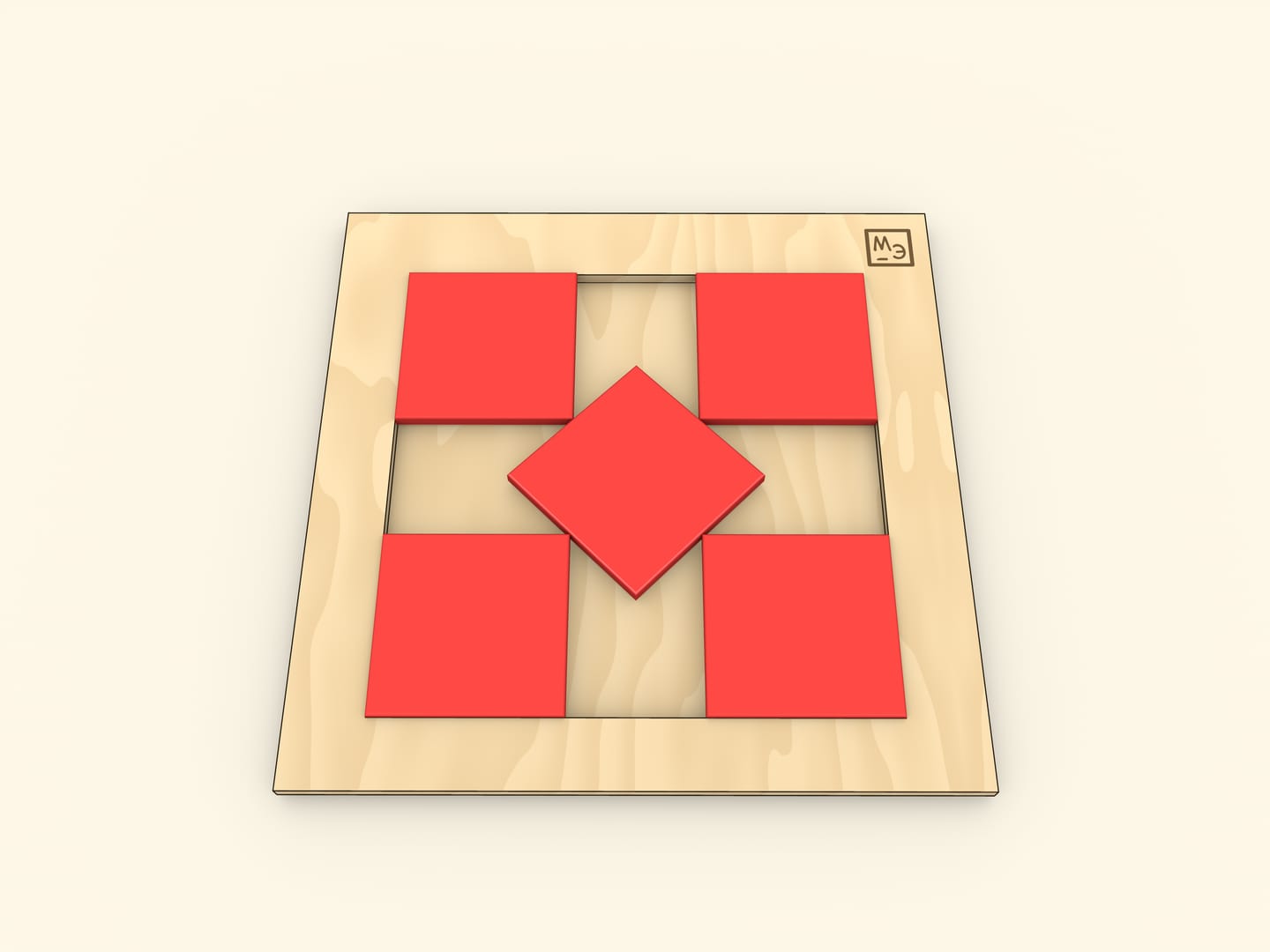
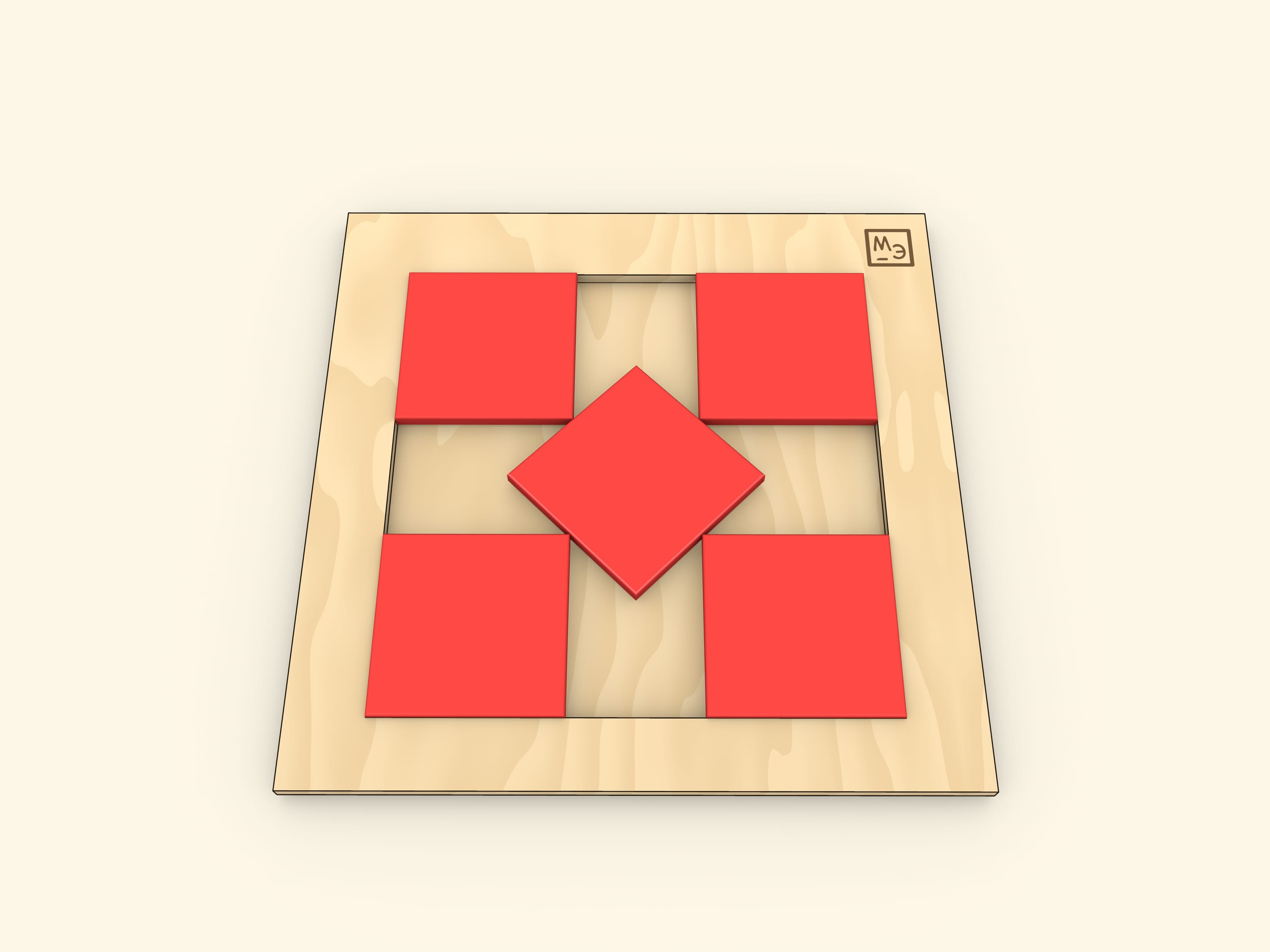
Квадраты укладываются в квадрат.
Пять единичных квадратов можно уложить в квадрат со стороной $2+1/\sqrt{2}$. Десять единичных квадратов укладываются в квадрат со стороной $3+1/\sqrt{2}$. И хотя пример известен с 1979 года, доказательство того, что в квадрат с меньшей стороной уложить десять квадратиков нельзя, появилось лишь в 2003 году.
Квадраты укладываются в правильный треугольник.
Шесть единичных квадратов можно уложить в правильный треугольник со стороной $2+4/\sqrt{3}$. В некоторых случаях, как представленное для восьми квадратов (сторона треугольника примерно равна $5{,}3$), известное решение и нерегулярно, и некрасиво. Мир так устроен или ещё не нашли наилучший способ укладки?
Правильные треугольники укладываются в квадрат.
Три треугольника с единичной стороной можно уложить в квадрат со стороной $\sqrt{3}/2+\sqrt{6}/4$, а семь треугольников — в квадрат со стороной $2$.
Правильные треугольники укладываются в круг.
Восемь треугольников с единичной стороной можно уложить в круг с радиусом, равным примерно $1{,}26$. А 19 треугольников можно уложить в круг радиуса $\sqrt{10/3}$ и это расположение было найдено совсем недавно — в 2019 году.
На сайте «Erich's Packing Center» приведено множество подобных примеров. Про некоторые решения можно доказать, что они наилучшие, некоторые решения — наилучшие известные примеры на момент обновления. Иногда удивляет, что даже для «простых» фигур и «простых» ответов, как в случае упаковки 6 и 13 квадратов в квадрат, доказательство было найдено только в XXI веке.
Каждый может выбрать понравившиеся ему примеры и сделать соответствующие головоломки, попроще или посложнее.