Парабола: изонить⁠

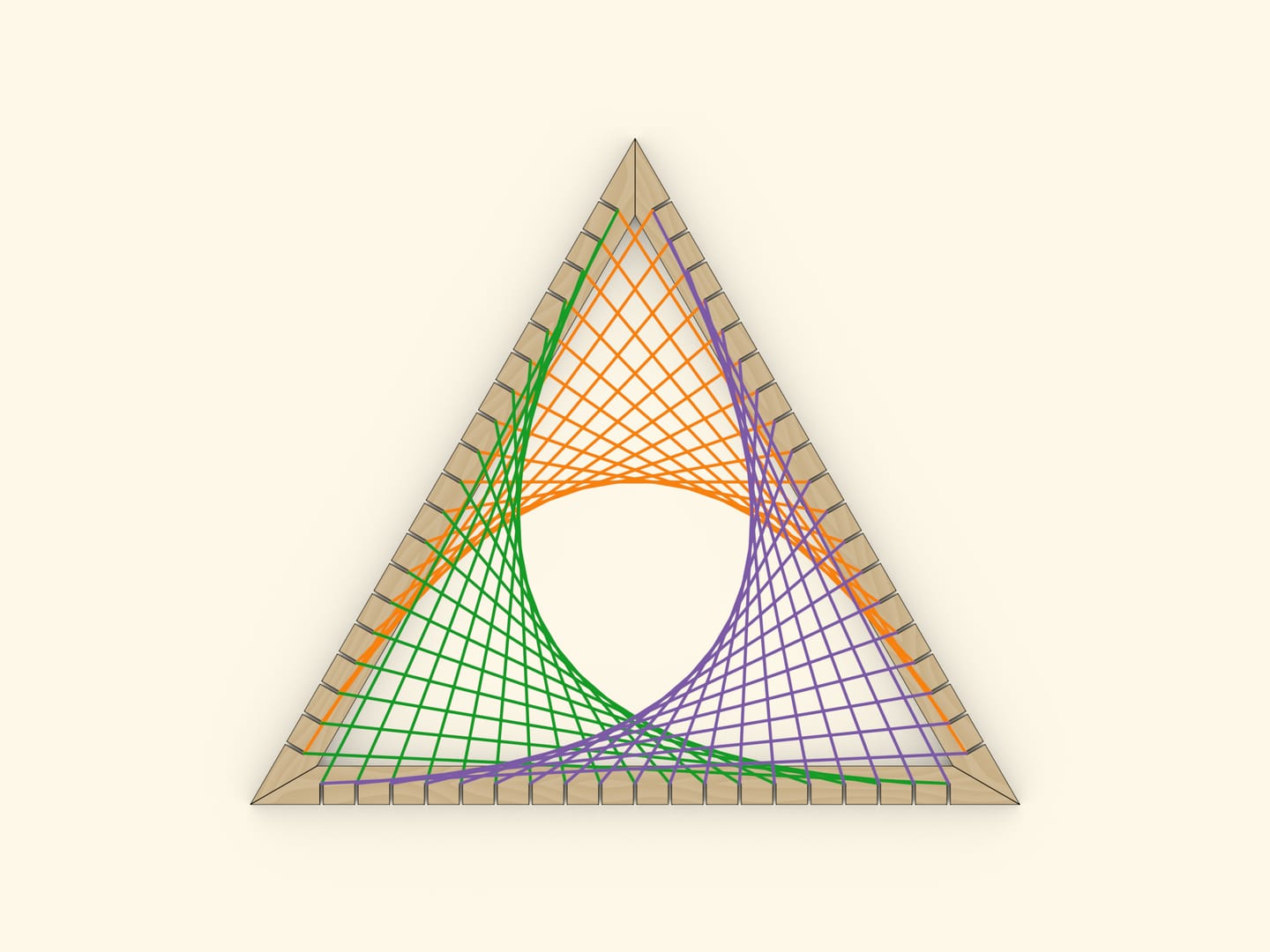
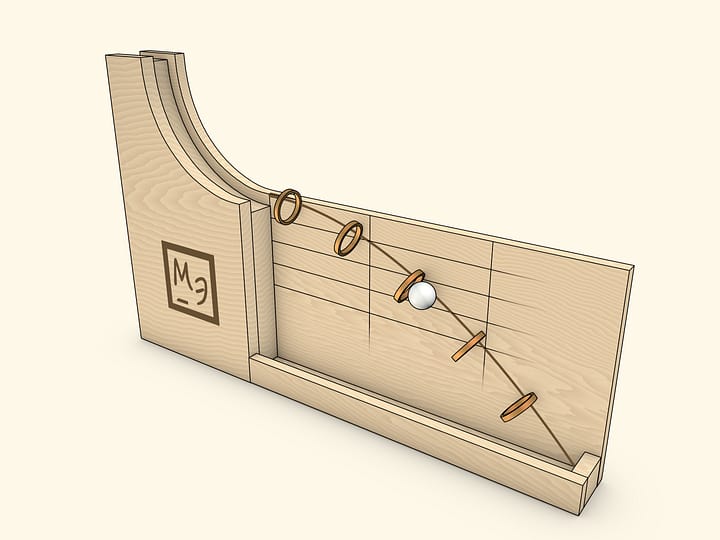
Всего лишь натя­ну­тые прямые нити, а выри­со­вы­ва­ется кар­тина. Такая тех­ника назы­ва­ется string art, curve stitching, изонить, вышивка по кар­тону. Эти слова можно встре­тить и когда гово­рят о дет­ском твор­че­стве, и когда гово­рят об искус­стве. И даже когда гово­рят о науке: изо­нить поз­во­ляет уви­деть ⁠⁠кар­дио­иду и неф­ро­иду, лучше понять физи­че­ское явле­ние «кау­стика» и его матема­ти­че­скую основу — геомет­ри­че­ское поня­тие «оги­бающая». А в пред­став­лен­ной модели изо­нить выри­со­вы­вает пара­болу.

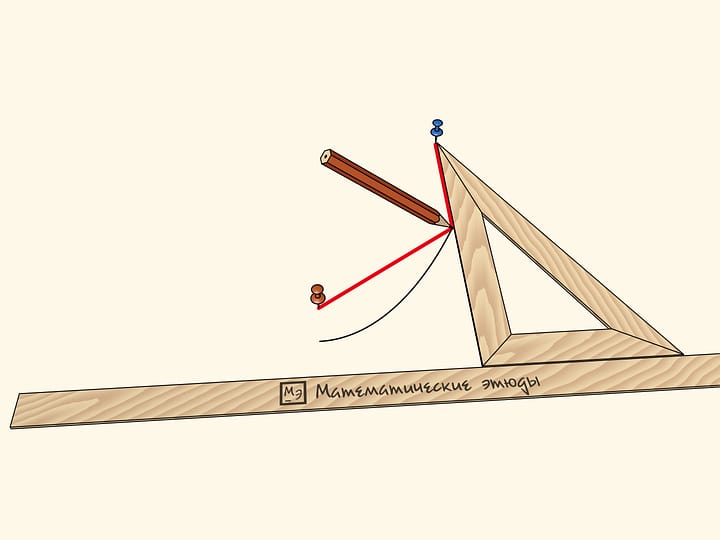
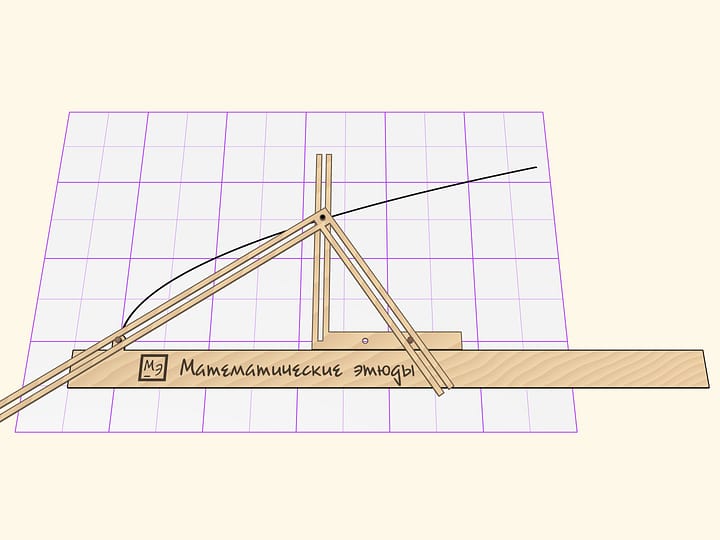
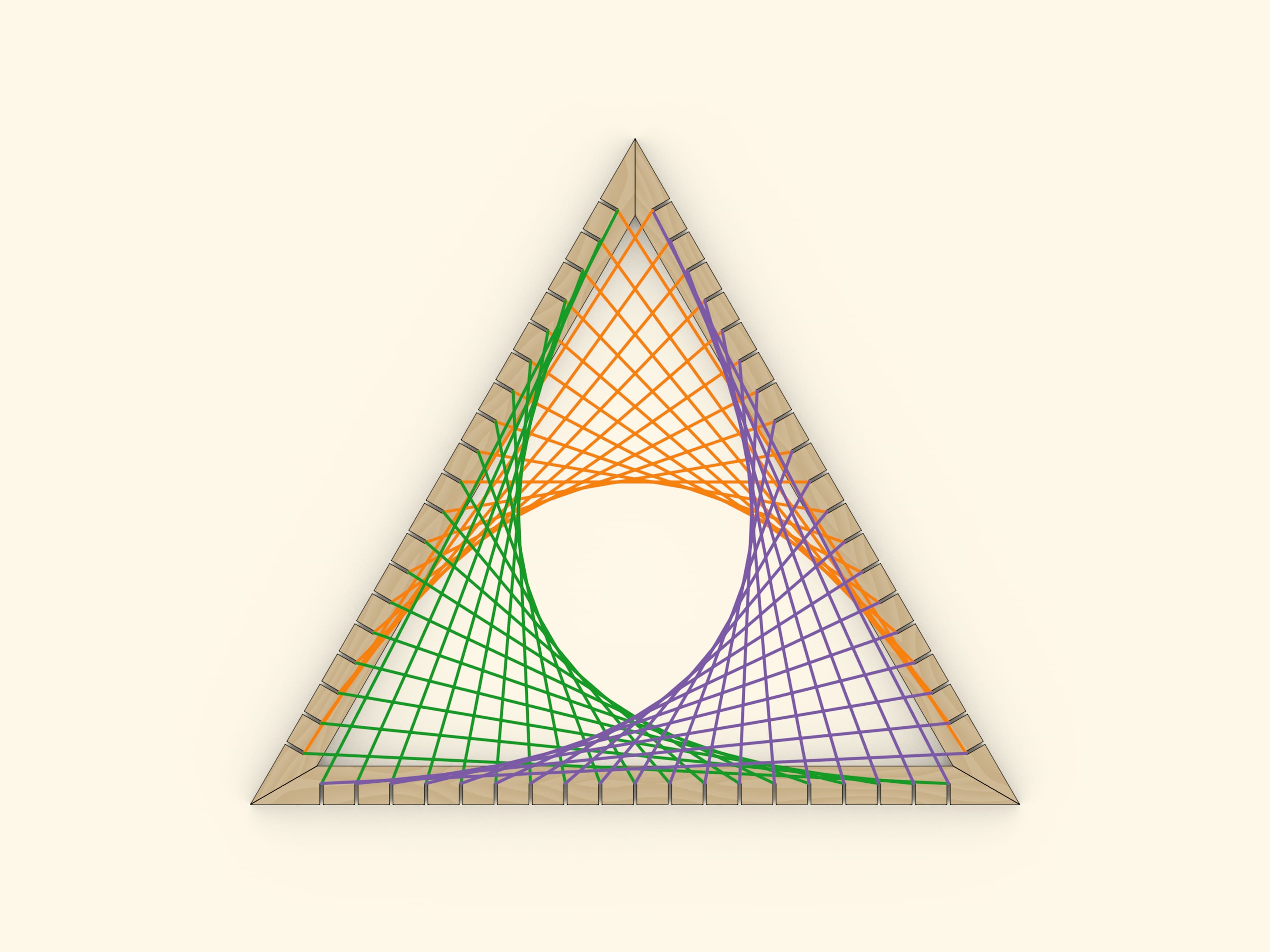
На сто­ро­нах про­из­воль­ного угла отме­тим оди­на­ко­вое коли­че­ство точек так, чтобы шаг между точ­ками на каж­дой из сто­рон был посто­ян­ным. Зануме­руем их на одной сто­роне «от вершины угла», а на дру­гой сто­роне — «к вершине угла». Если соеди­нить нитями точки с оди­на­ко­выми номе­рами, то уви­дим пара­болу!

В «симмет­рич­ном слу­чае», — когда «шаг» между точ­ками на обеих сто­ро­нах оди­на­ко­вый, — ось пара­болы будет совпа­дать с высо­той тре­уголь­ника. Если от вершины тре­уголь­ника и от осно­ва­ния отступить оди­на­ко­вое коли­че­ство шагов, то вершина пара­болы будет лежать на сред­ней линии тре­уголь­ника; несложно постро­ить и положе­ние фокуса пара­болы. Если шаги между точ­ками на раз­ных сто­ро­нах отли­чаются, то пара­бола будет «повёр­нута» отно­си­тельно тре­уголь­ника.

Раз­лич­ные реа­ли­за­ции этой идеи встре­чаются и как дет­ское твор­че­ство, и как элемент в про­из­ве­де­ниях искус­ства.

Дока­за­тельство, что полу­чающа­яся при таком постро­е­нии оги­бающая явля­ется пара­бо­лой, осно­вы­ва­ется на том, что при аффин­ном пре­об­ра­зо­ва­нии пара­бола пере­хо­дит в пара­болу (заме­тим, что при этом фокус и дирек­триса не пере­хо­дят в фокус и дирек­трису). Так общий слу­чай сво­дится к част­ному, когда тре­уголь­ник рав­но­бед­рен­ный и прямо­уголь­ный; а точки рас­по­ложены на сто­ро­нах без отступов от углов. А этот слу­чай в точ­но­сти совпа­дает с постро­е­нием пара­болы в мини­а­тюре ⁠⁠Пара­бола как оги­бающая.

Это дока­за­тельство ана­логично реше­нию сле­дующей задачи о двух пеше­хо­дах. По пере­се­кающимся прямым с раз­лич­ными ско­ро­стями идут два пеше­хода, при­чём точку пере­се­че­ния прямых они про­хо­дят в раз­ные моменты времени. Ока­зы­ва­ется, оги­бающая все­возмож­ных прямых, соеди­няющих пеше­хо­дов, явля­ется пара­бо­лой.