Псевдосфера — поверхность Бельтрами — является поверхностью постоянной отрицательной гауссовой кривизны. Постоянство гауссовой кривизны во всех точках поверхности имеет интересную механическую интерпретацию: кусочек поверхности можно двигать по самой поверхности, и он, изгибаясь, всё время будет прилегать к ней. Без математических знаний в случае псевдосферы это кажется удивительным.
Два важнейших и простейших примера поверхностей постоянной гауссовой кривизны — плоскость и сфера.
Плоскость является примером поверхности нулевой гауссовой кривизны. Листочек — кусочек плоскости — можно сдвигать по ней, поворачивать, и листочек всегда будет прилегать к плоскости. Листочек можно перевернуть и снова положить на плоскость. (Кроме того, из листочка можно свернуть цилиндр и конус, для которых уже не так очевидно, что это поверхности постоянной нулевой кривизны.)
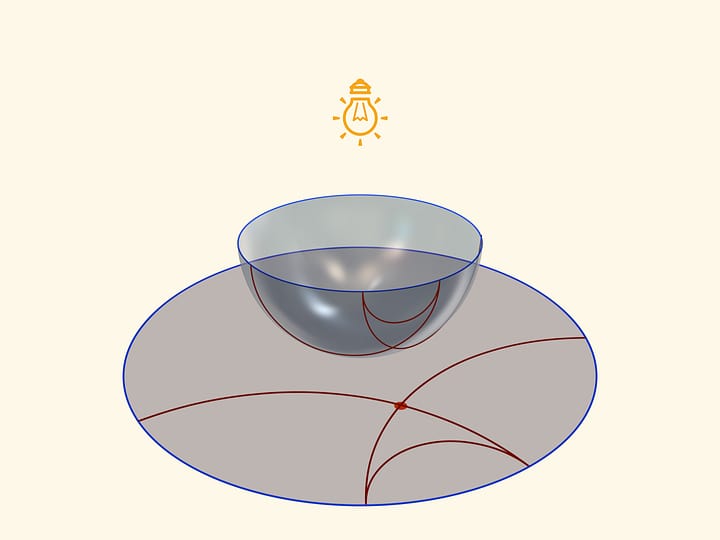
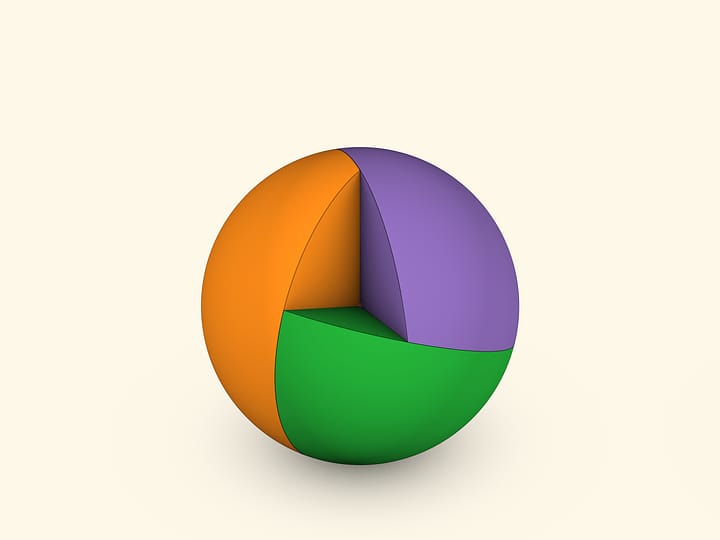
Гауссова кривизна во всех точках сферы радиуса $R$ одинакова и равна $1/R^2$. Сферическую шапочку можно двигать по сфере, поворачивать относительно центра шапочки и она всегда будет прилегать к сфере. Но если попробовать перевернуть шапочку, то приложить её к сфере не удастся.
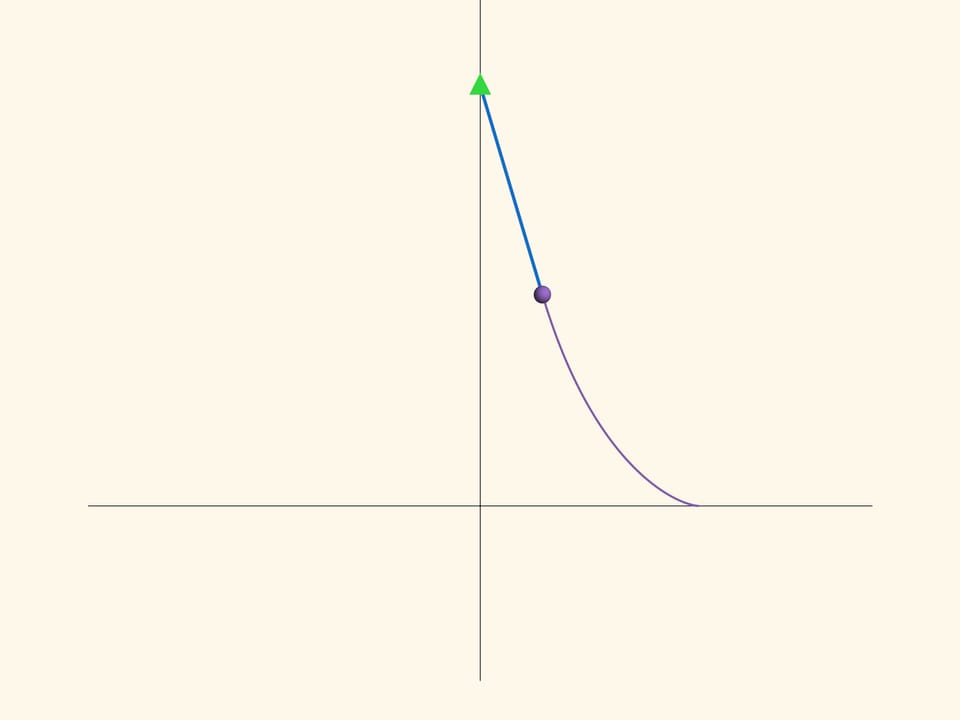
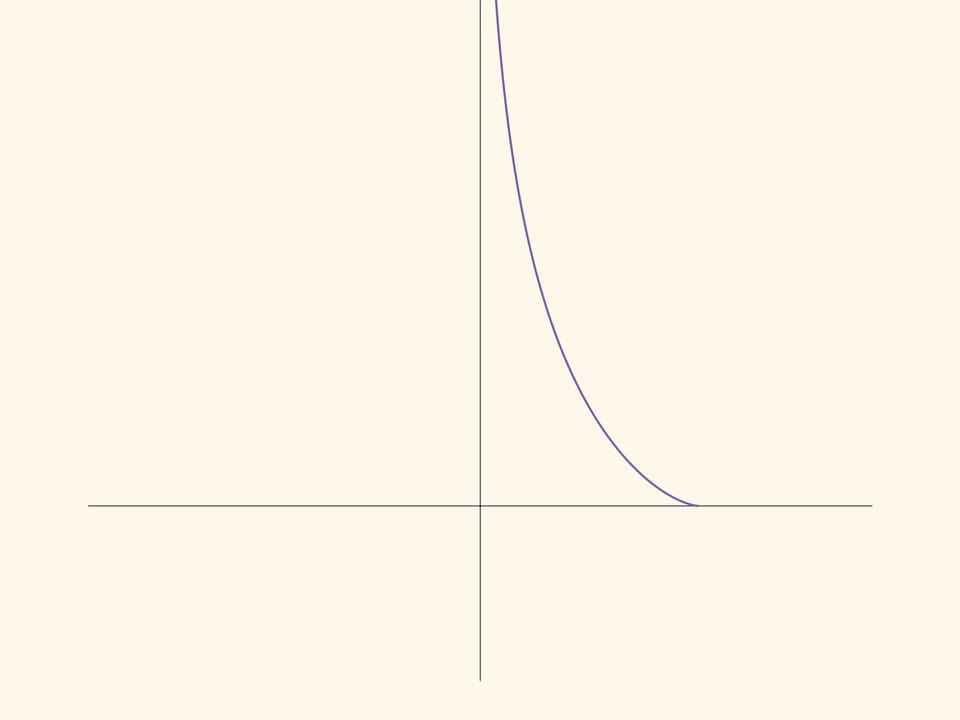
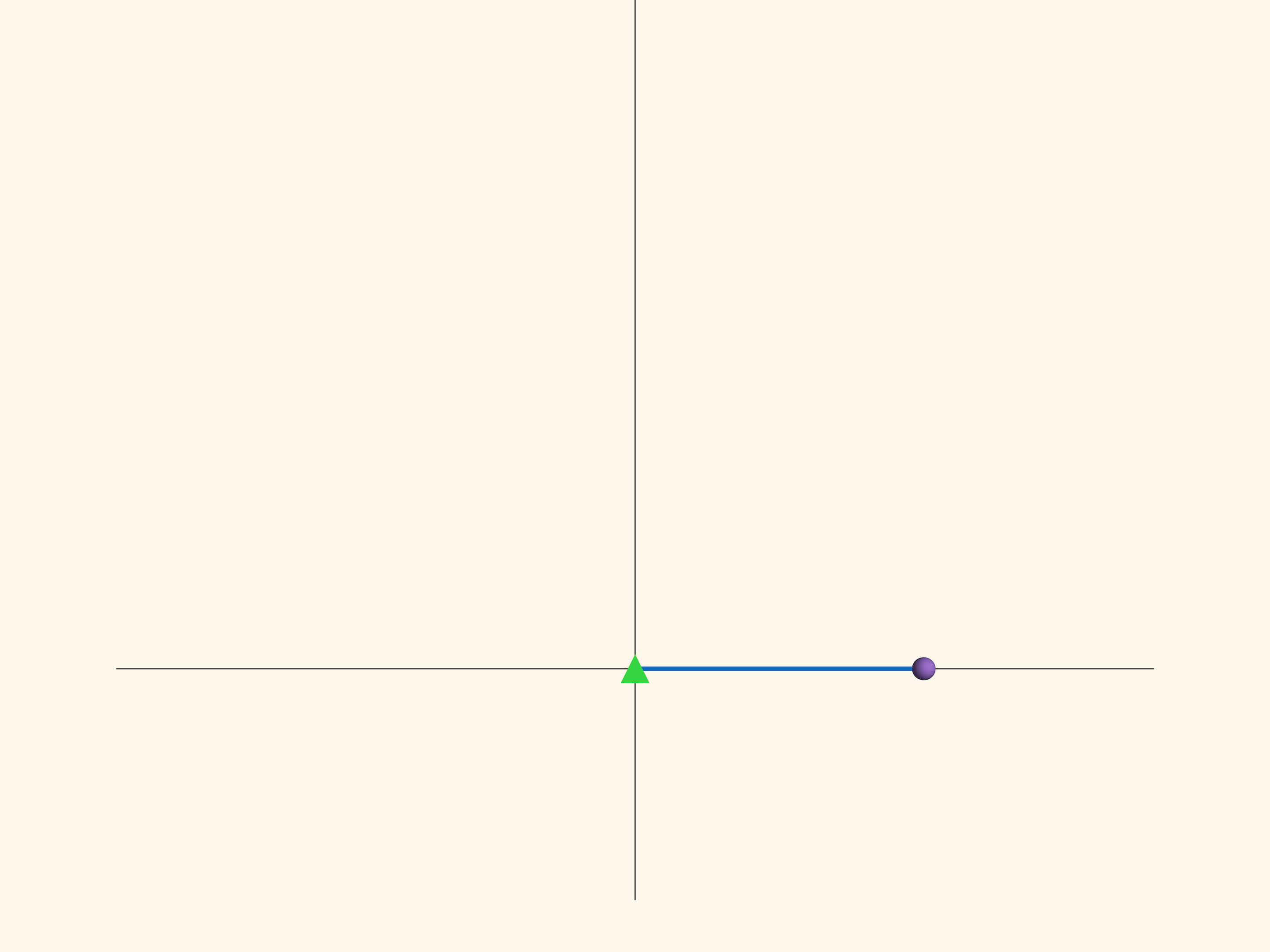
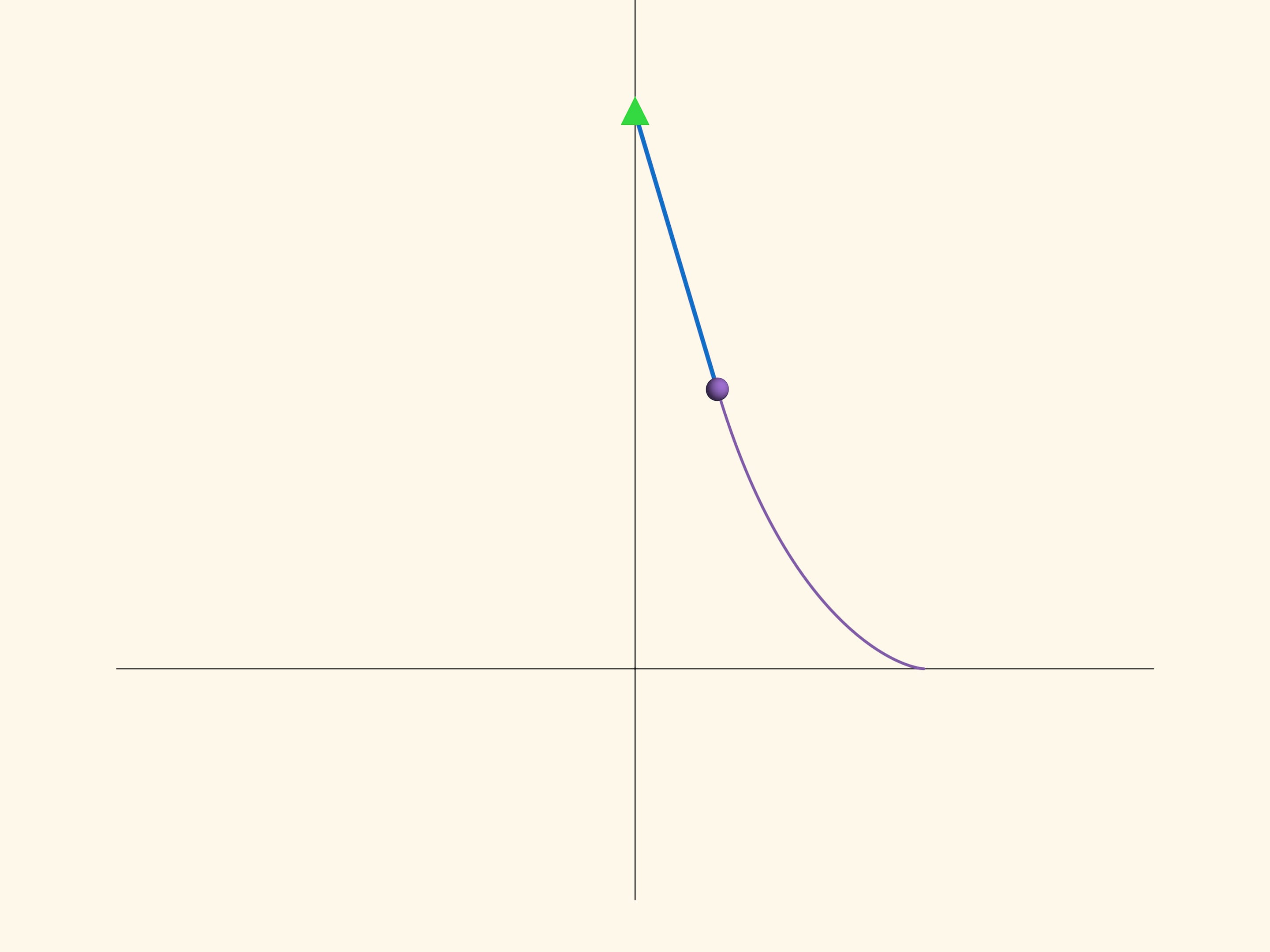
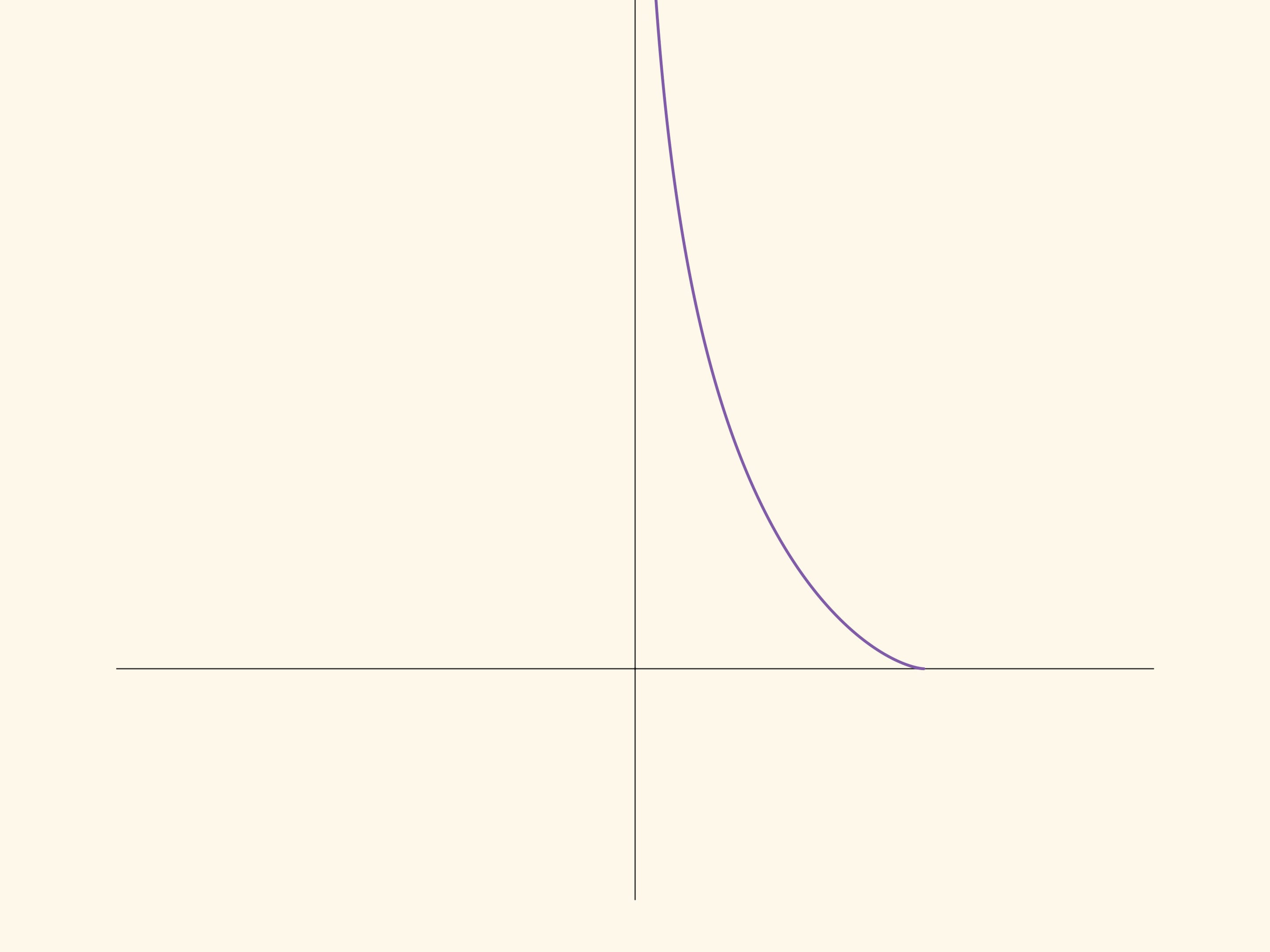
Трактриса — плоская кривая, описываемая точкой («тяжёлым телом»), которую тащат на верёвке постоянной длины $R$, идя по прямой $l$. Положения верёвки при этом являются касательными к трактрисе, а сама кривая приближается к прямой $l$, но не достигает её.
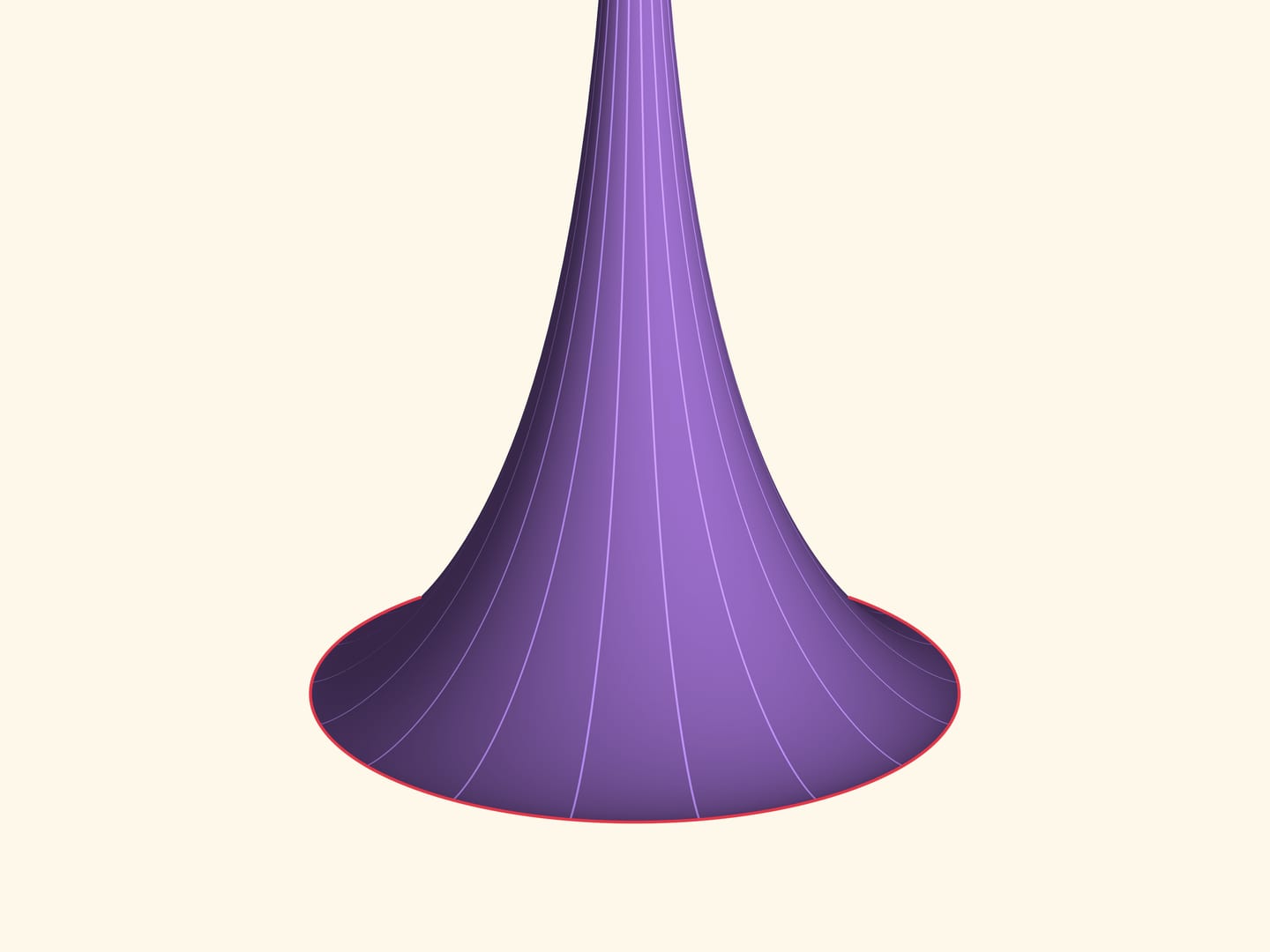
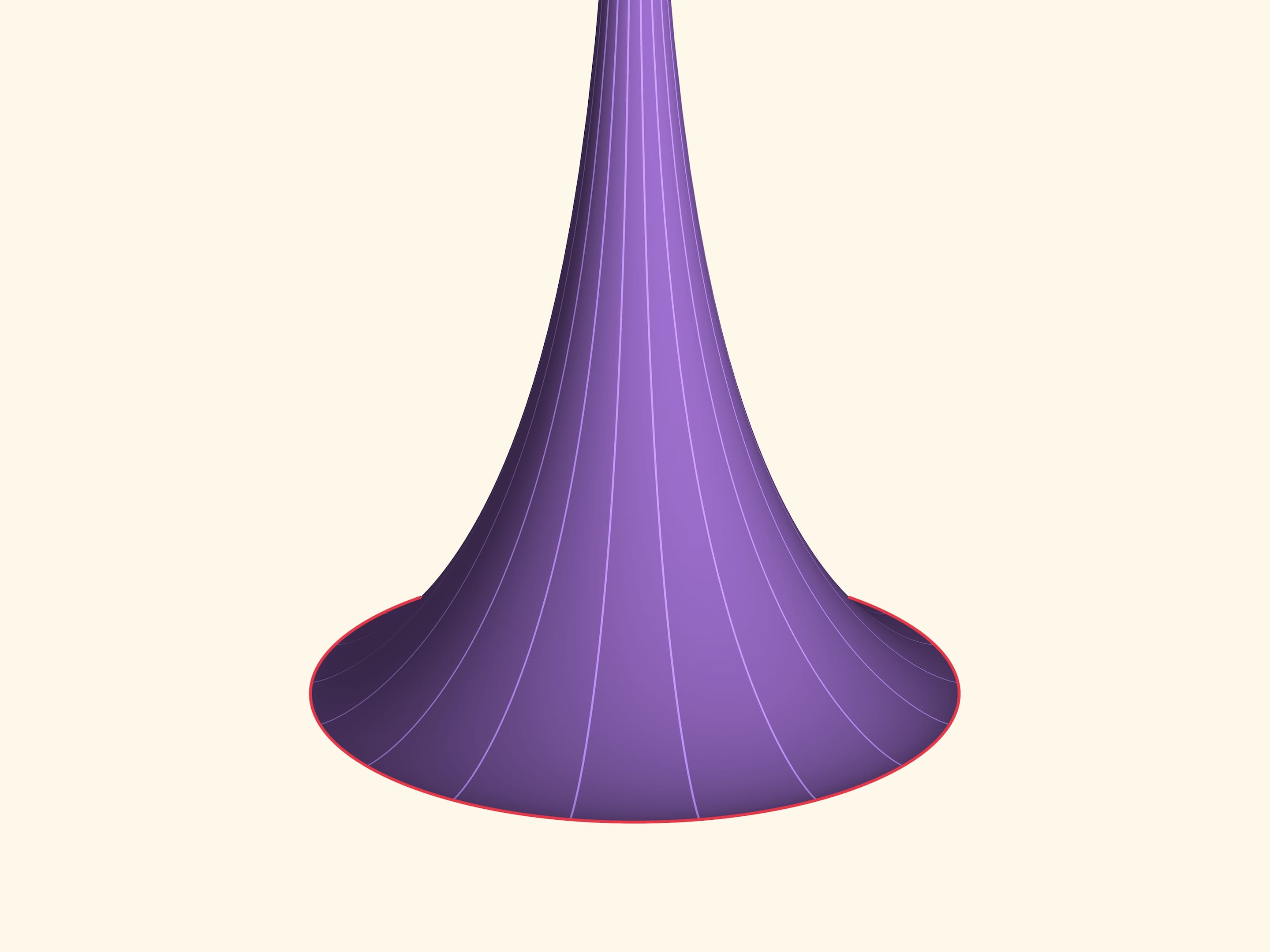
Если провращать трактрису вокруг прямой $l$, получится бесконечная поверхность. В фильме показана половина трактрисы и половина поверхности. Полностью поверхность бесконечна в обе стороны, во всех точках гладкая, кроме ребра возврата, являющегося окружностью радиуса $R$.
В 1693 году Христиан Гюйгенс заметил, что площадь этой поверхности и ограничиваемый ею объём конечны: площадь равна $4\pi R^2$ и совпадает с площадью сферы радиуса $R$, а объём в два раза меньше объёма шара радиуса $R$.
В первой половине XIX века российский математик немецкого происхождения Фердинанд Миндинг показал, что поверхность имеет постоянную отрицательную гауссову кривизну, равную $-1/R^2$. Кроме того, он показал, что понятия группы движений и конгруэнтных фигур имеют смысл лишь на поверхностях постоянной кривизны.
А во второй половине XIX века, уже после смерти и Николая Ивановича Лобачевского, и Карла Фридриха Гаусса, и Яноша Бойяи, итальянский математик Эудженио Бельтрами доказал, что на гладкой части этой поверхности, вложенной в трёхмерное пространство, локально реализуется геометрия плоскости Лобачевского и назвал поверхность псевдосферой.
Гауссова кривизна поверхности в точке равна произведению главных кривизн в этой точке. На плоскости и на сфере значения главных кривизн не меняются от точки к точке. Псевдосфера — более сложная и интересная поверхность постоянной кривизны: главные кривизны меняются, а вот произведение их значений, $-1/R^2$ — нет. И несмотря на это…
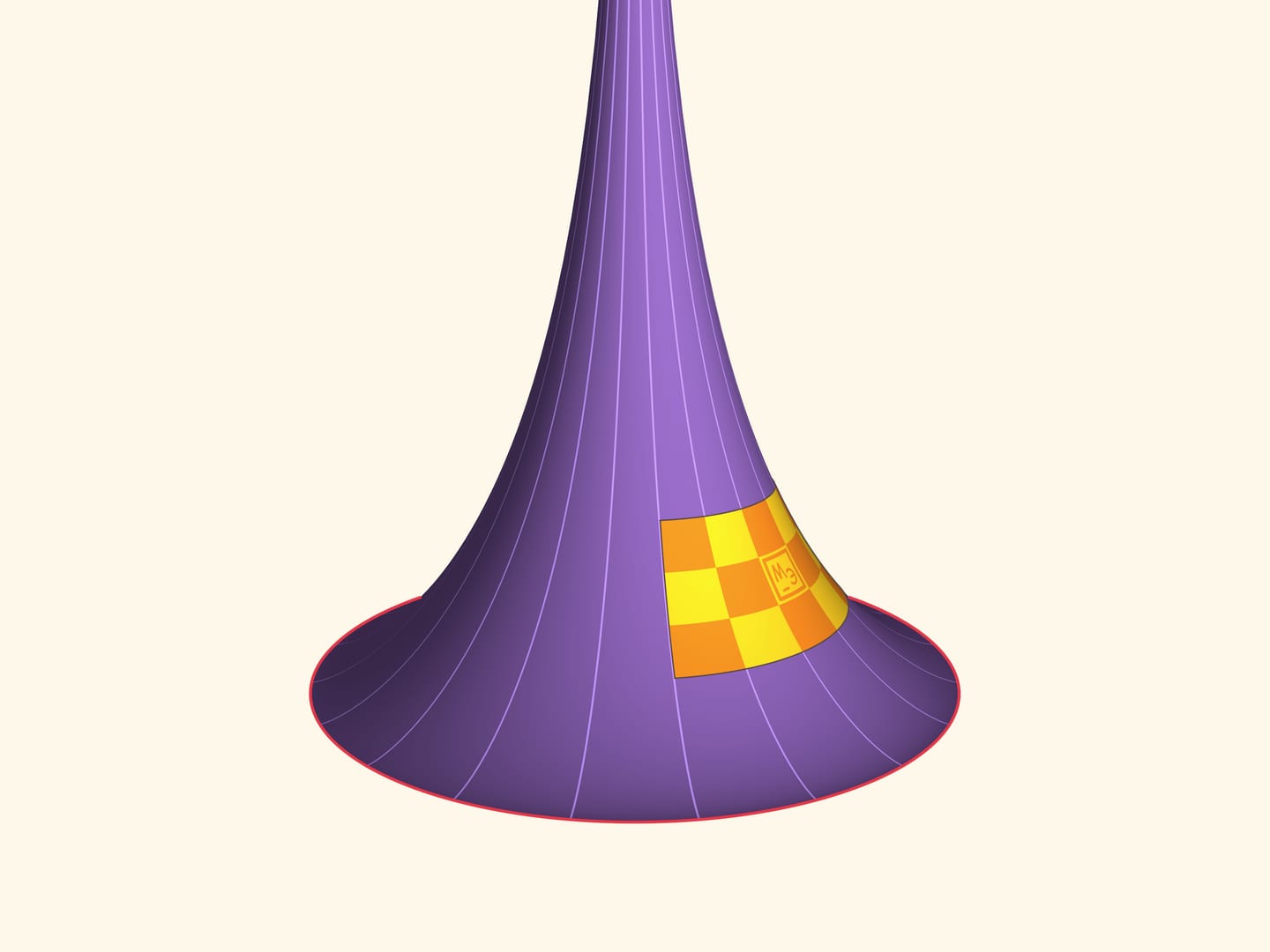
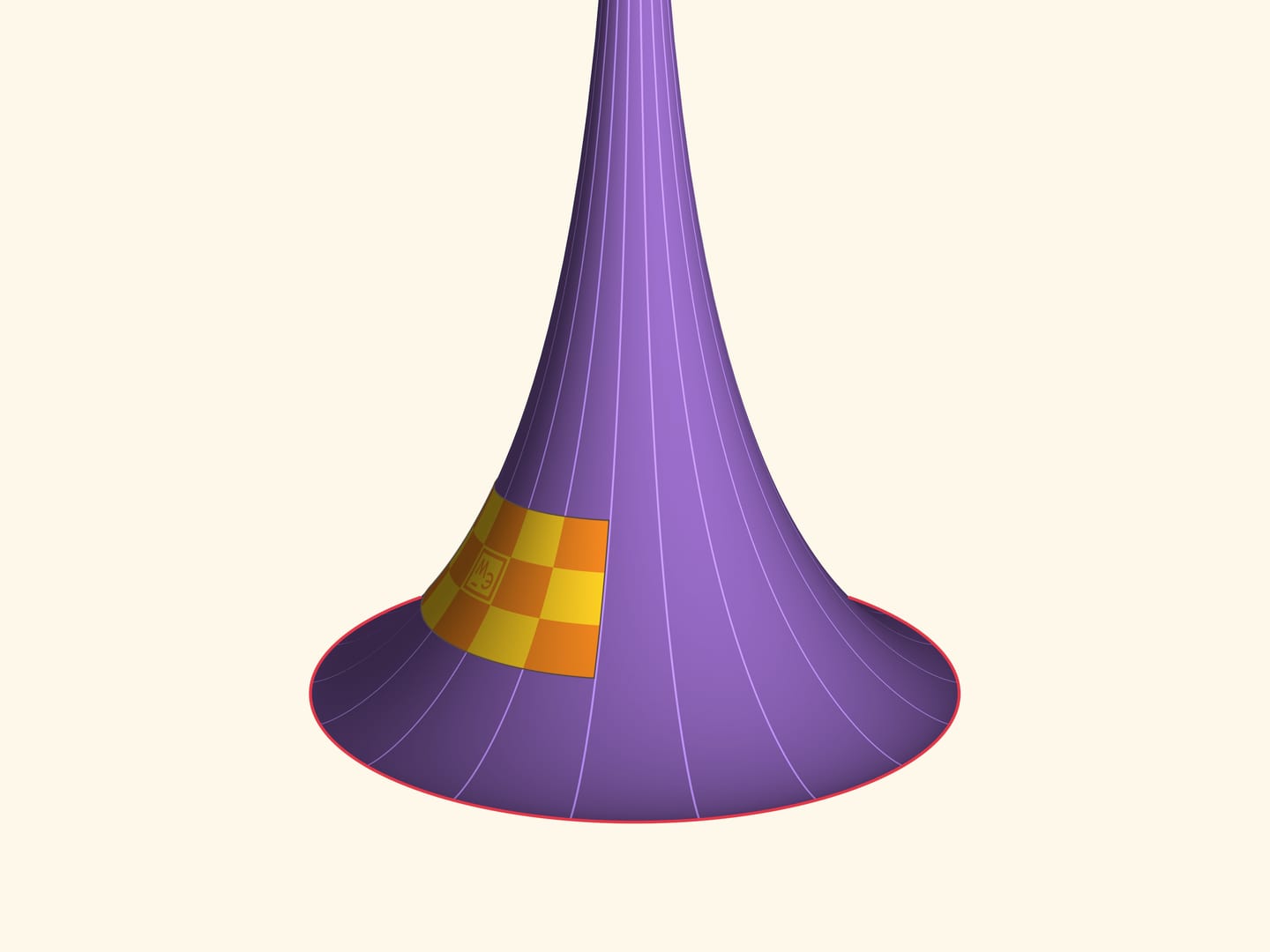
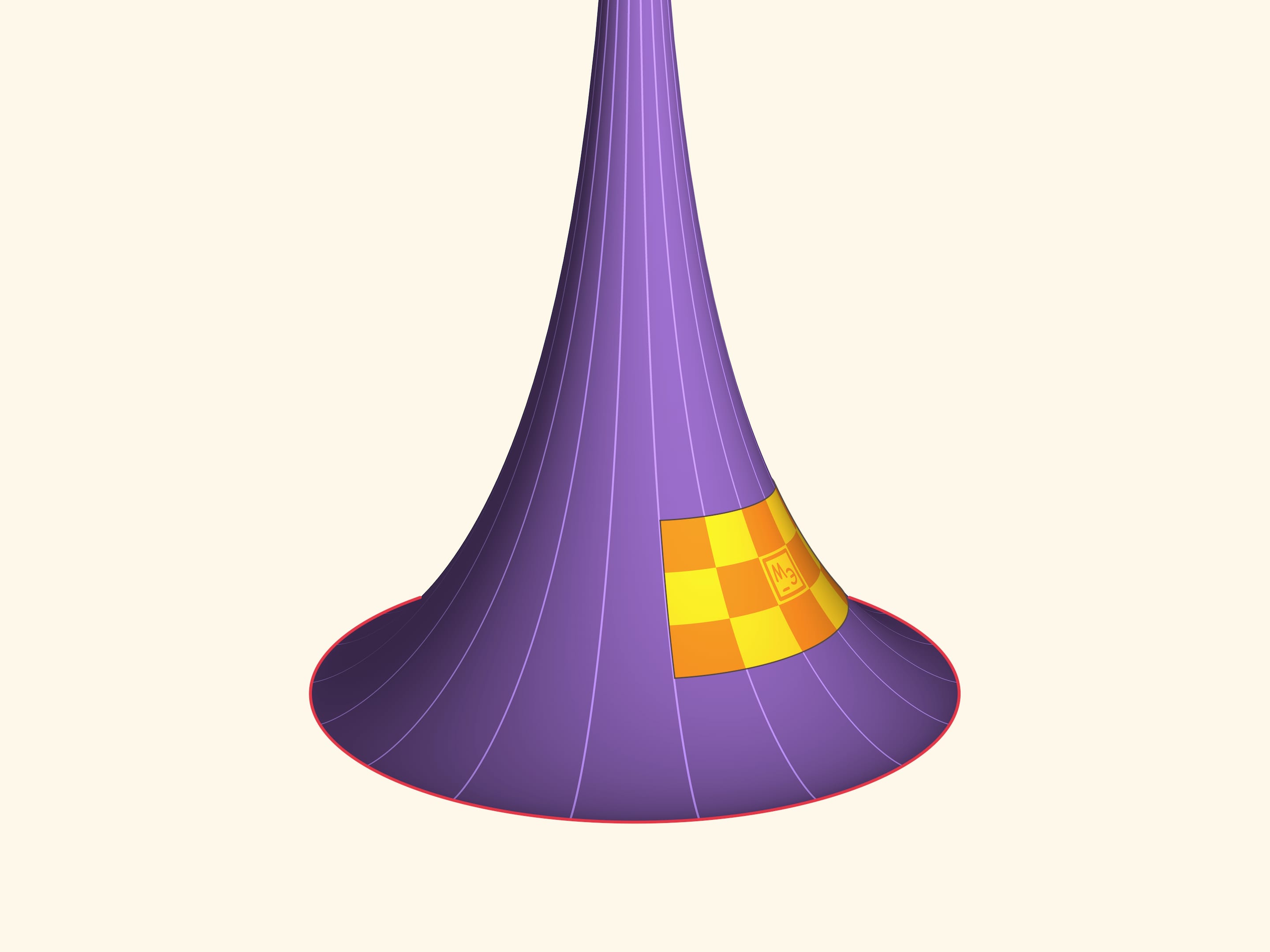
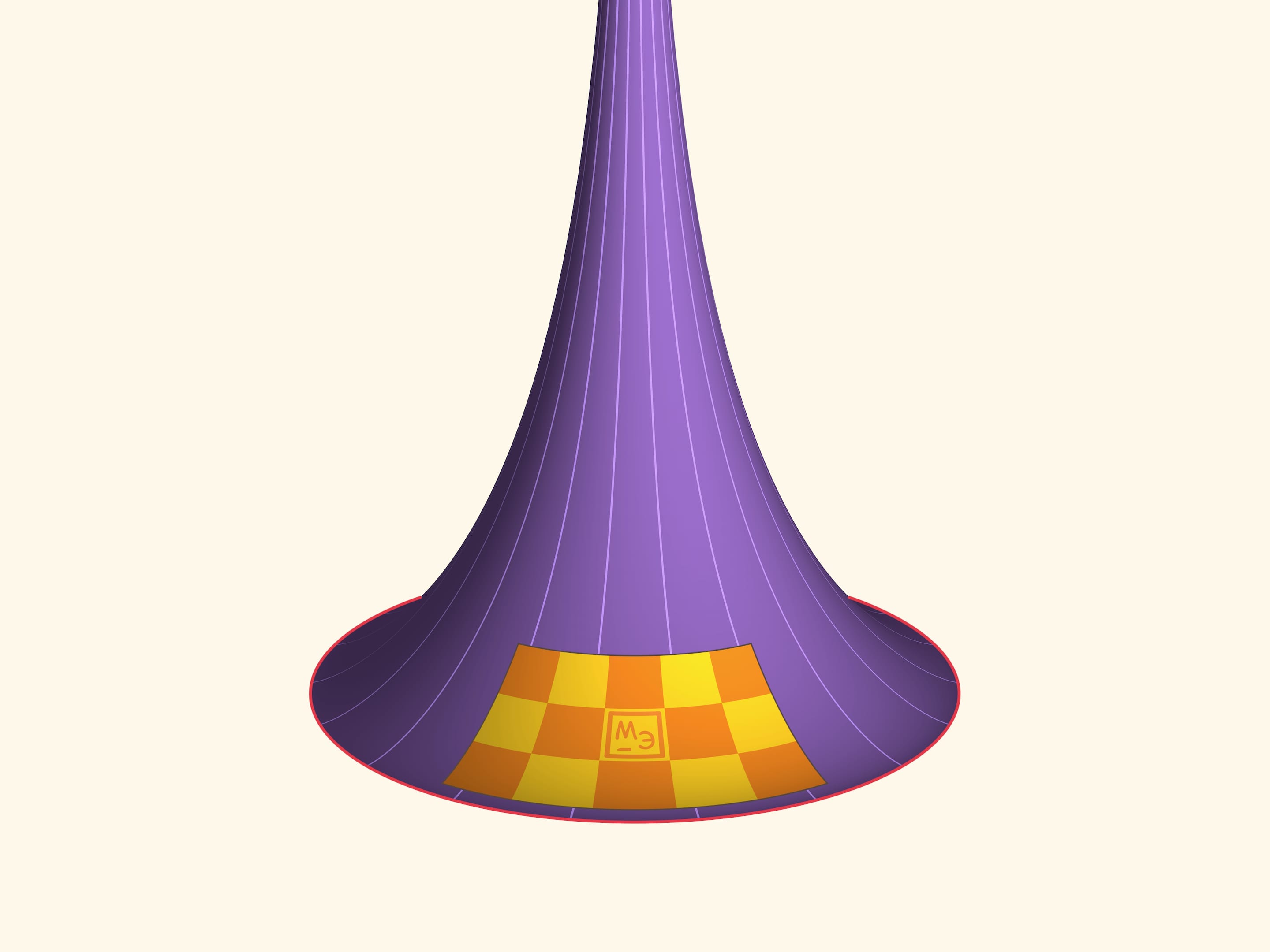
Возьмём некоторый кусочек поверхности Бельтрами. Сделаем пластину из изгибаемого, но нерастяжимого материала, например, меди, в форме этого кусочка поверхности. Эта пластина, имеющая отрицательную гауссову кривизну, может (как и плоский лист бумаги) изгибаться, и при этом расстояния по поверхности между точками пластины не меняются. По знаменитой теореме Гаусса, названной им самим «egregium» (замечательной), гауссова кривизна зависит только от внутренней геометрии поверхности (т. е. расстояний по поверхности) и поэтому не меняется при изгибаниях. Значит, нашу пластину нельзя приложить ни к плоскости (имеющей нулевую кривизну), ни к сфере (имеющей положительную кривизну). А вот к псевдосфере можно приложить в любой точке и в любом положении!
Псевдосфера является поверхностью вращения, и пластину, очевидно, можно смещать вдоль параллели.
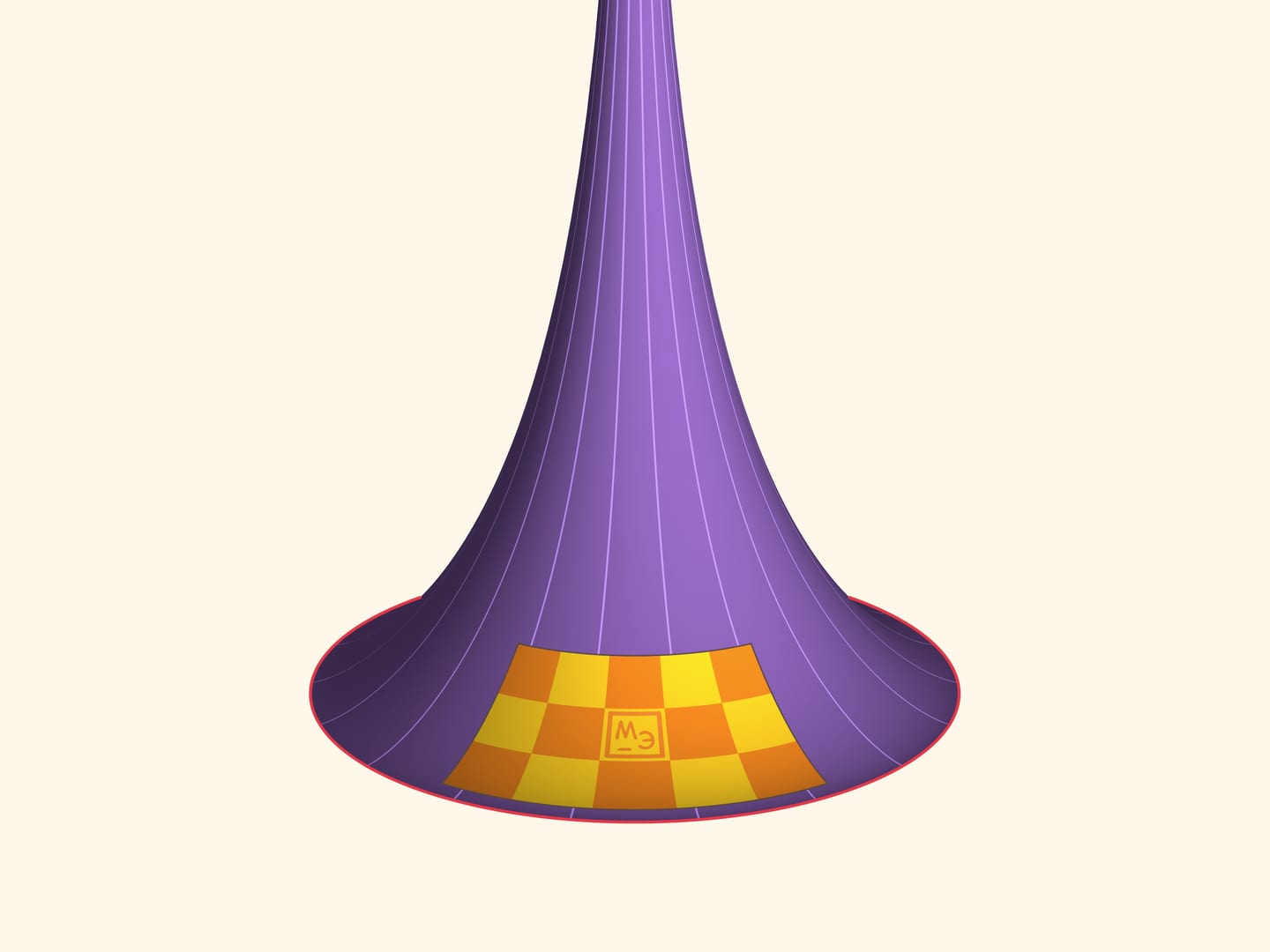
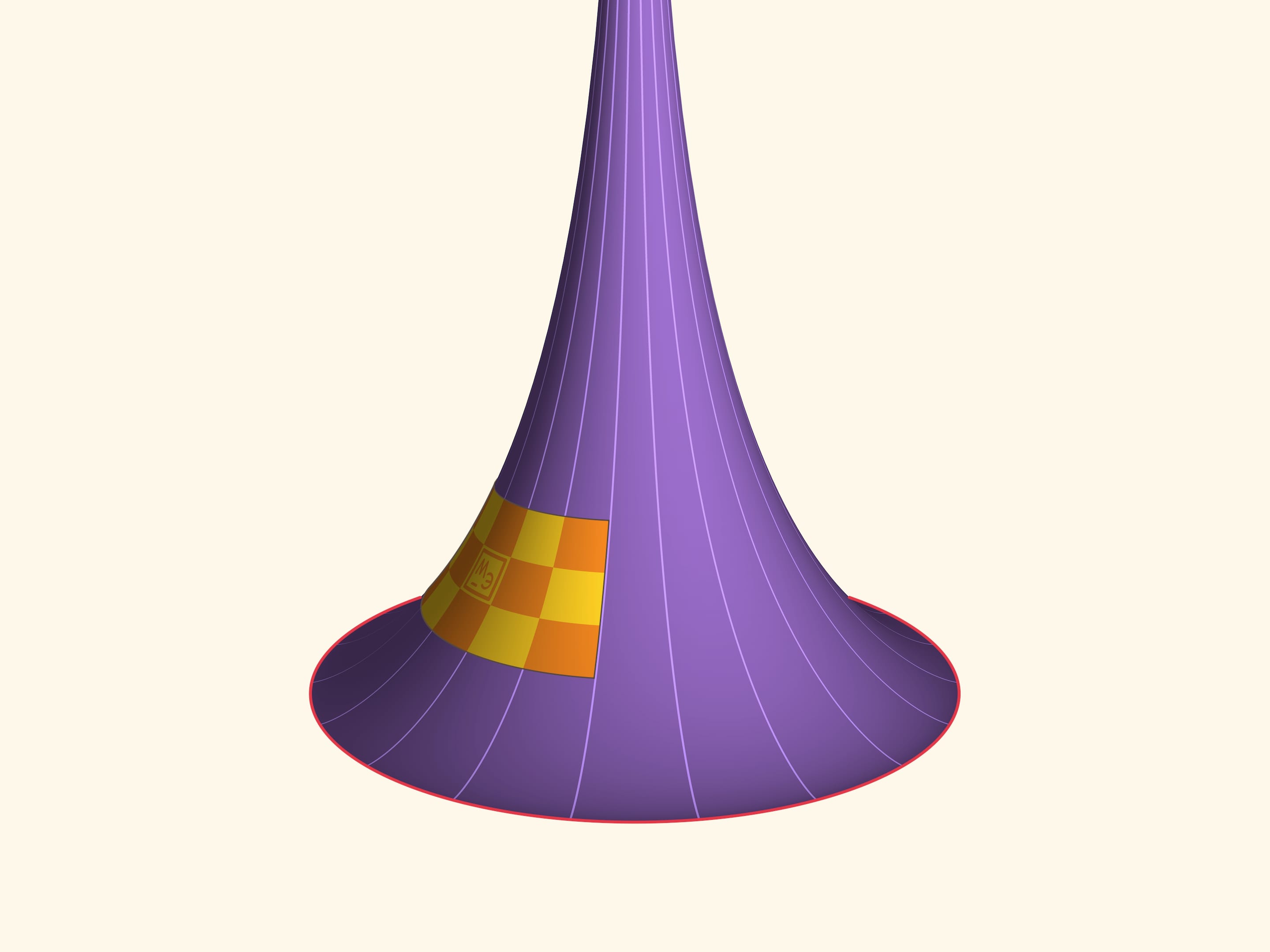
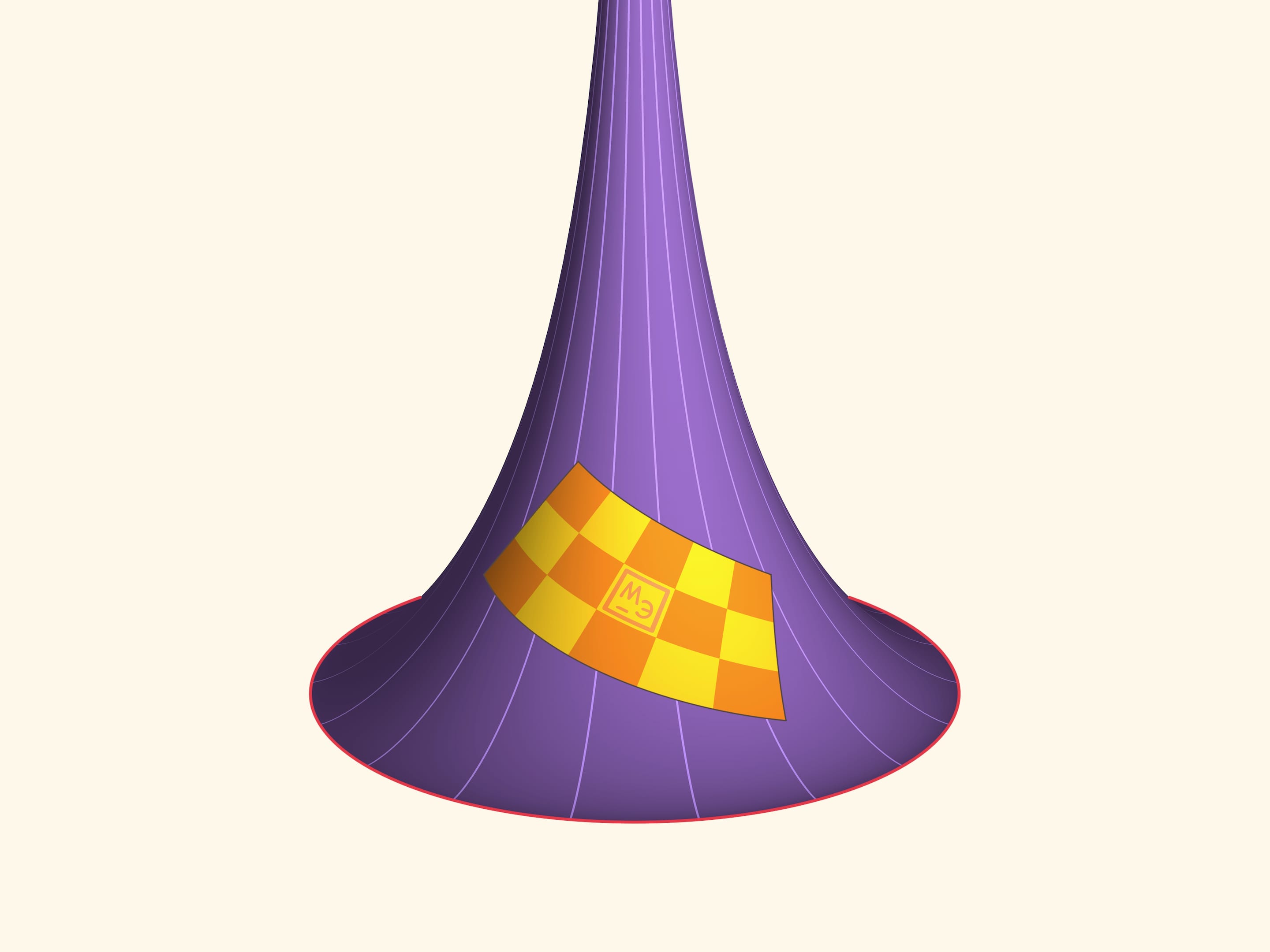
Менее очевидно, что пластину можно сдвигать по высоте вдоль поверхности.
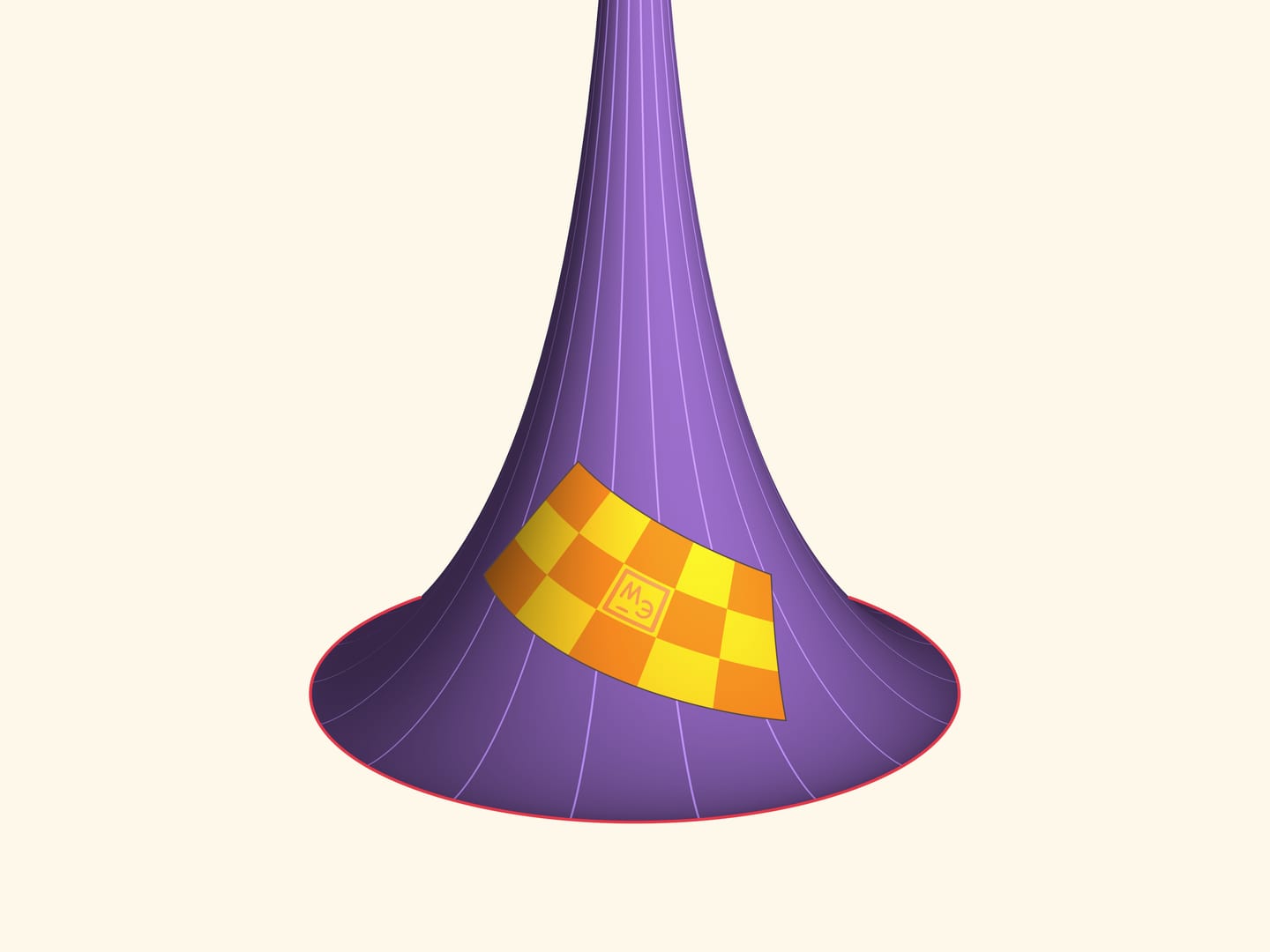
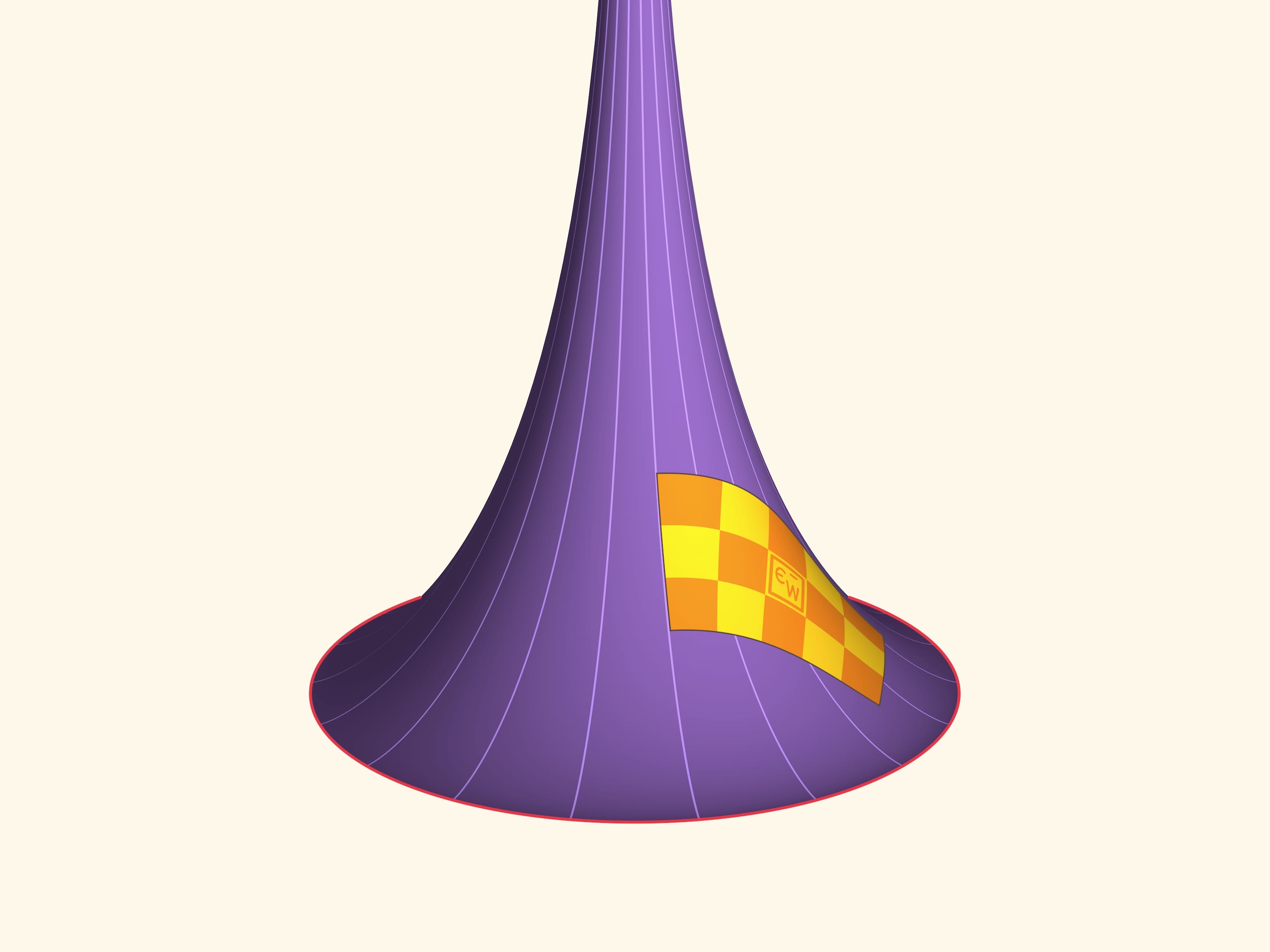
Без математических знаний не верится, но эту пластину можно вращать, и она всегда будет прилегать к поверхности!
Если из псевдосферы вырезать «средний слой» и посмотреть только на оставшиеся части, имеющие в точках совсем разные главные кривизны, то не верится даже, что пластину можно приложить и к одной части, и к другой.
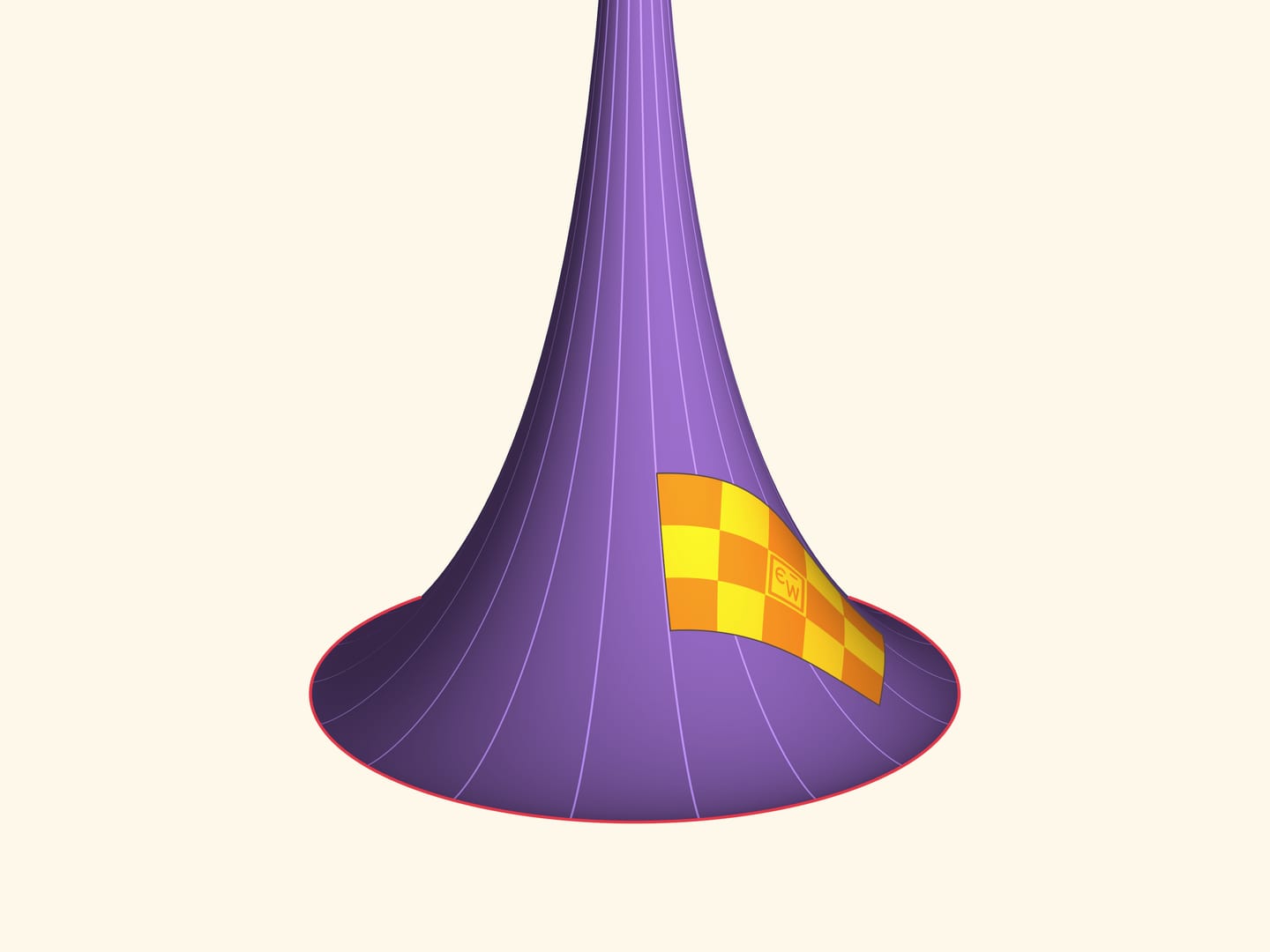
Ещё более интересный факт, подмеченный штатным краснодеревщиком лаборатории популяризации и пропаганды математики Математического института им. В. А. Стеклова РАН Александром Лещинским при изготовлении этой модели, заключается в том, что пластину можно «вывернуть наизнанку»: как и в случае листочка на плоскости её можно перевернуть, и она снова будет прилегать к поверхности Бельтрами! Выворачивание пластины связано с решениями важного нелинейного дифференциального уравнения в частных производных — уравнения sin-Гордона $\frac{\partial^2u}{\partial x\,\partial y}=\sin u$, и в следующей версии фильма мы покажем, как это выглядит.
Описанная модель, изготовленная на рубеже XIX—XX веков, как тогда было принято, из гипса, хранится в Музее Николая Ивановича Лобачевского Казанского федерального университета. Деревянная модель, с которой можно проводить эксперименты, находится в лаборатории популяризации и пропаганды математики Математического института им. В. А. Стеклова Российской академии наук, а также подарена в музеи Н. И. Лобачевского в Казани (Республика Татарстан) и Козловке (Чувашская республика).