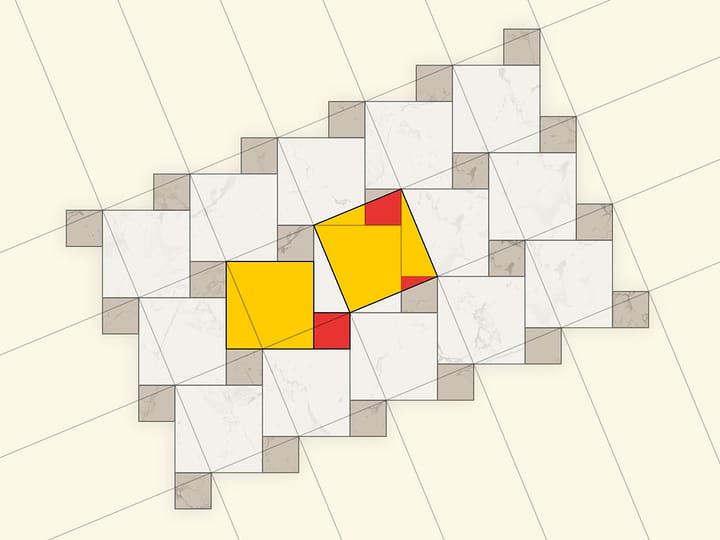
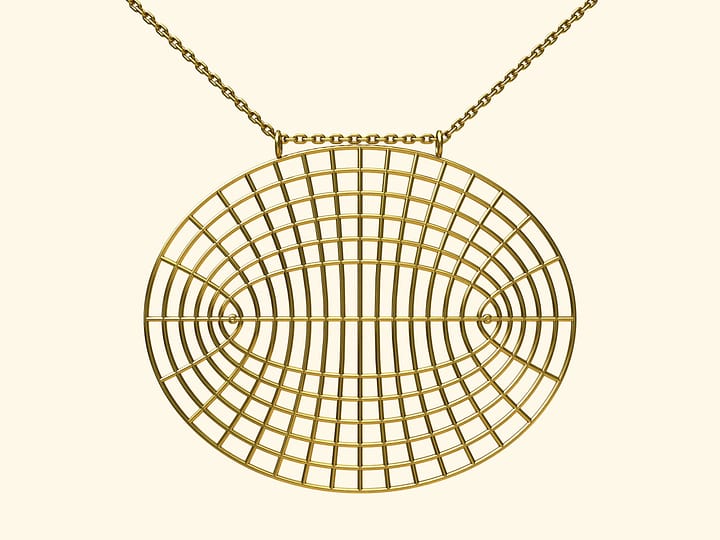
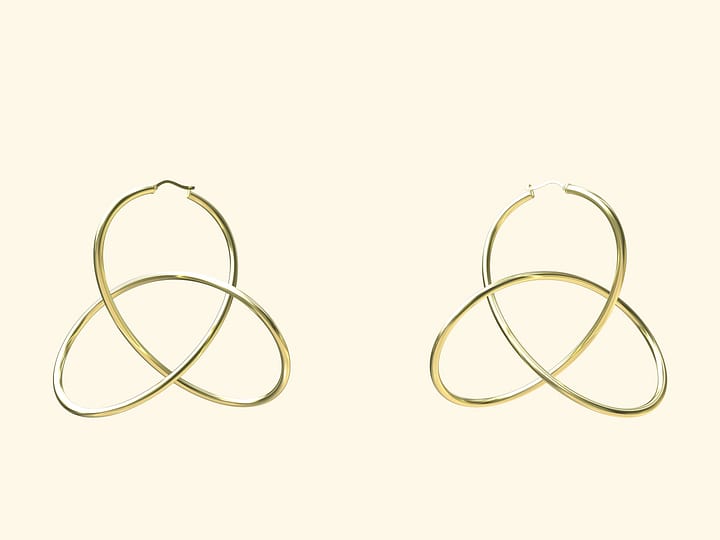Теорема Пифагора: серьги ⁠

⁠⁠Тео­рема Пифагора имеет много извест­ных дока­за­тельств типа «Смотри». Неко­то­рые из них можно пред­ста­вить и в совсем непри­выч­ном виде.

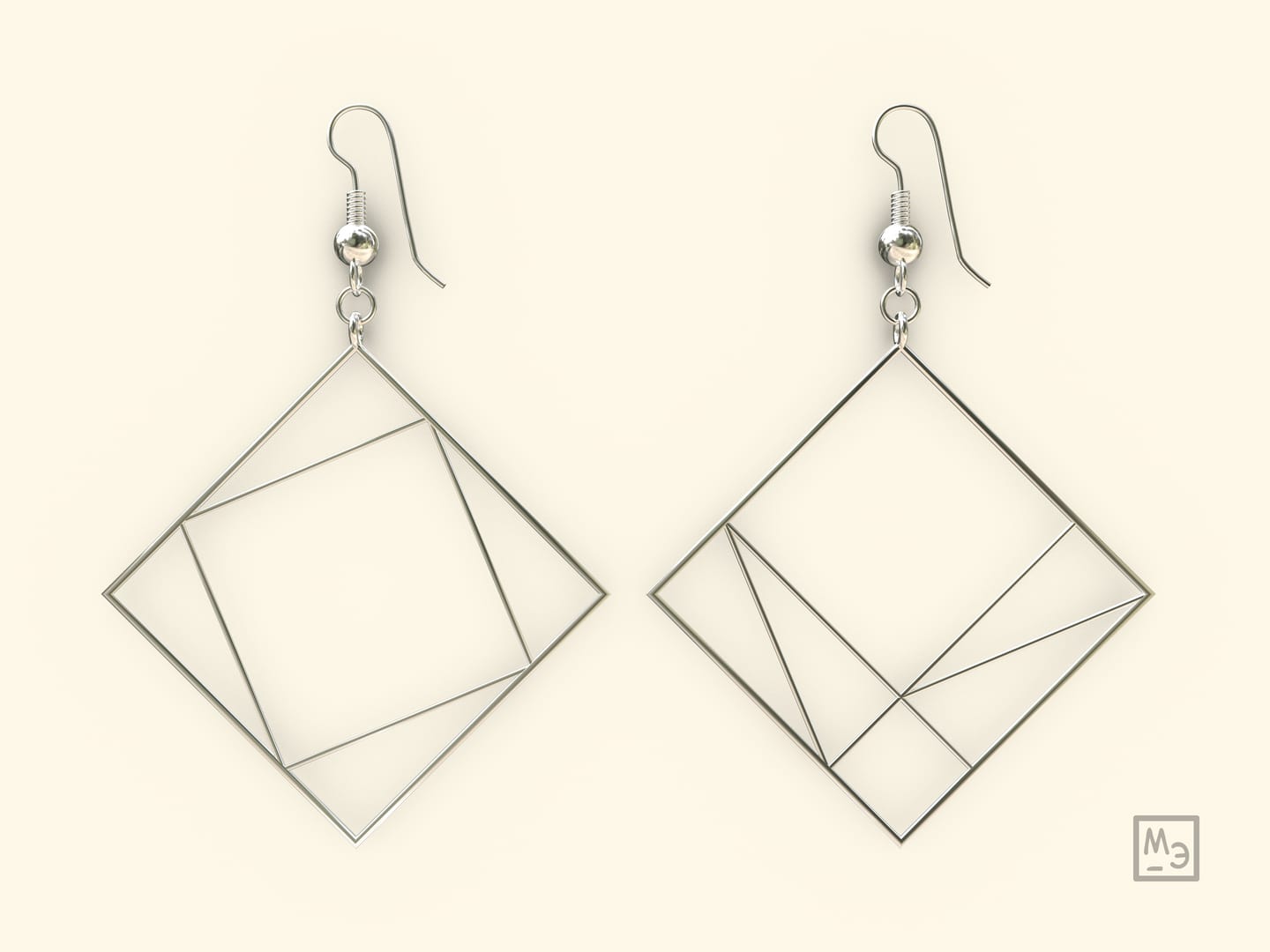
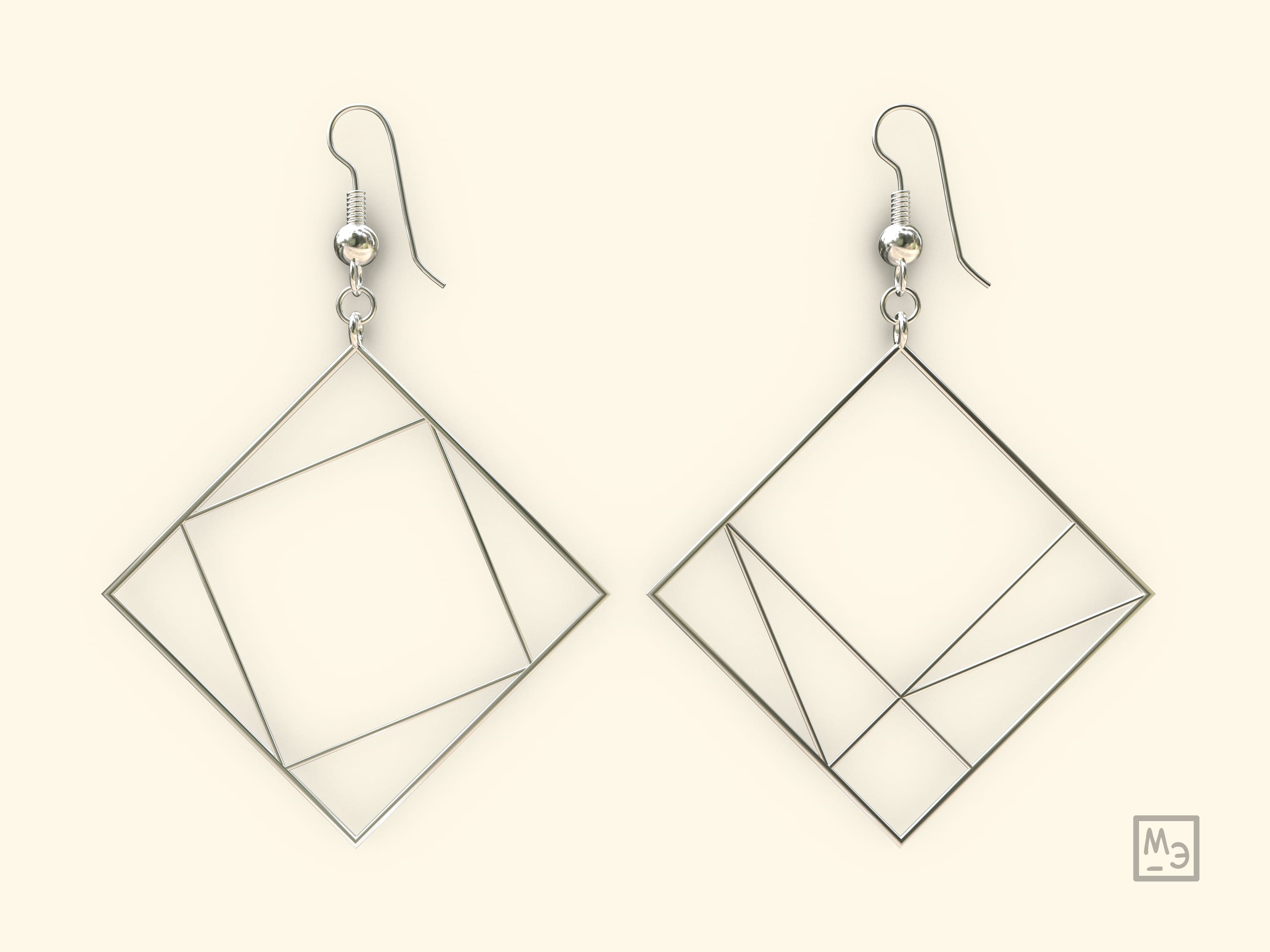
В одном наборе серьги должны быть раз­ные: именно вме­сте они достав­ляют дока­за­тельство тео­ремы Пифагора. Девушка с такими серьгами одно­значно при­вле­чёт внима­ние, а уж если она ещё и объяс­нит моло­дому чело­веку само дока­за­тельство тео­ремы…

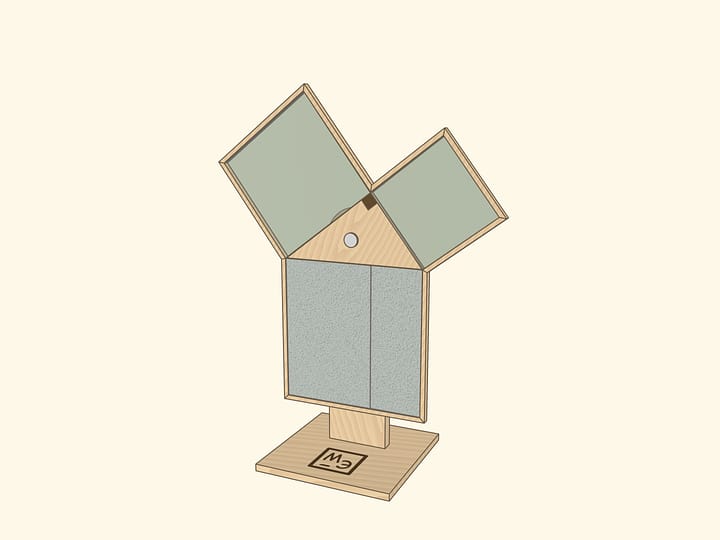
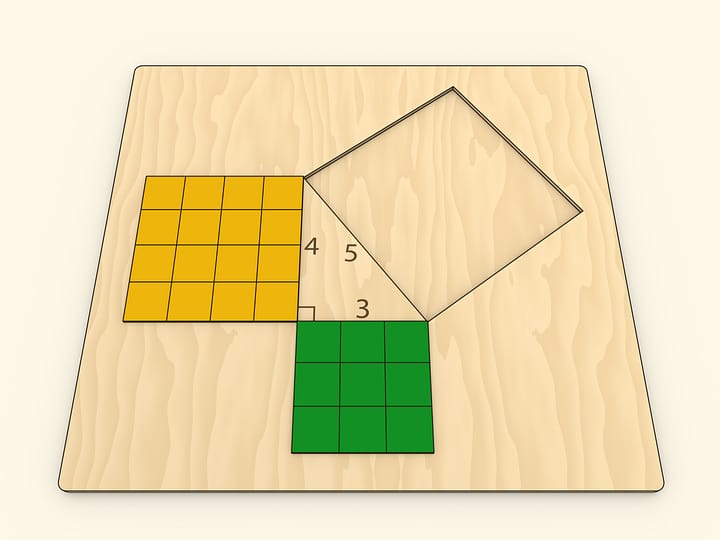
Это же дока­за­тельство можно реа­ли­зо­вать и как настоль­ную модель для класса.

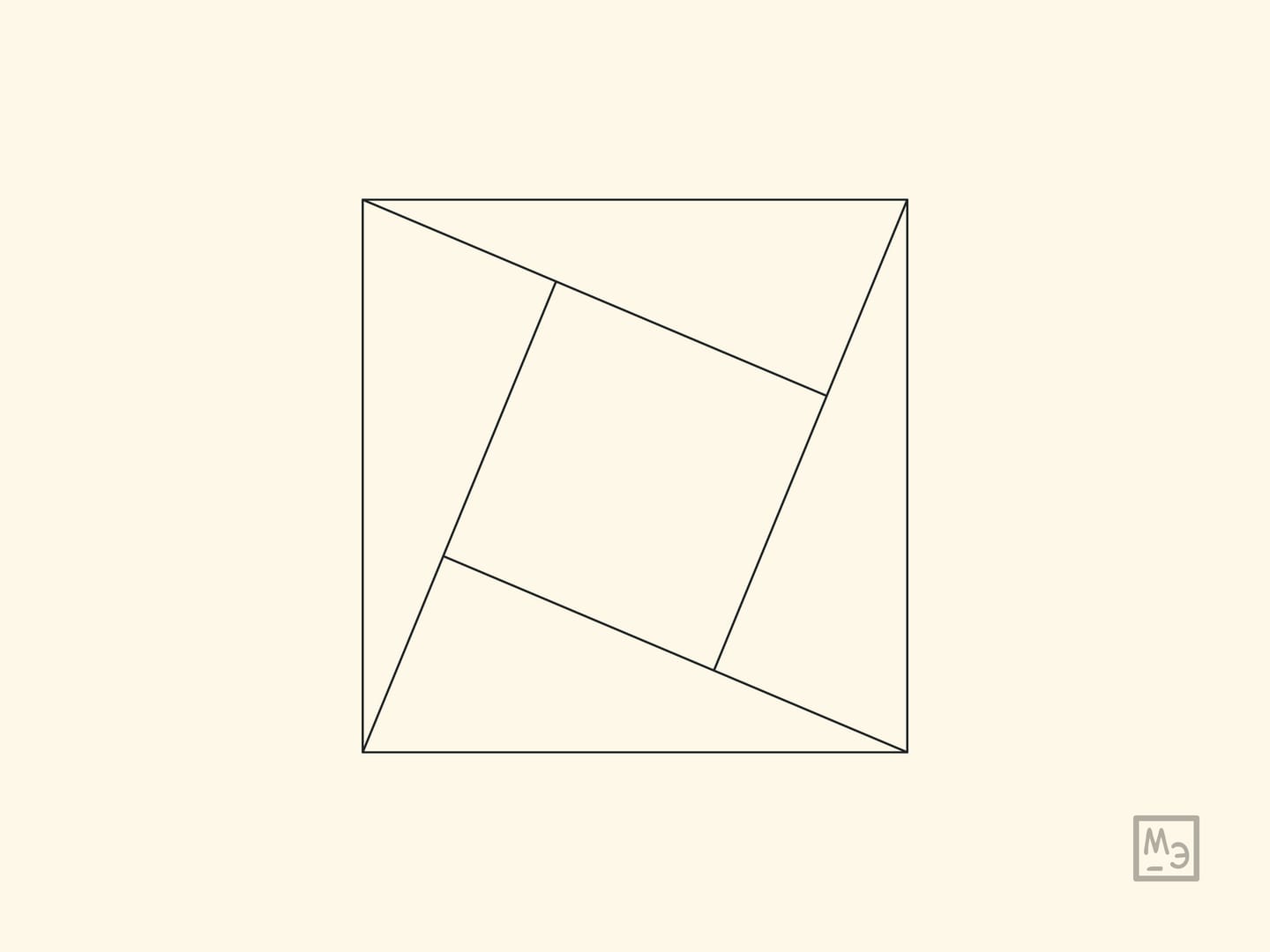
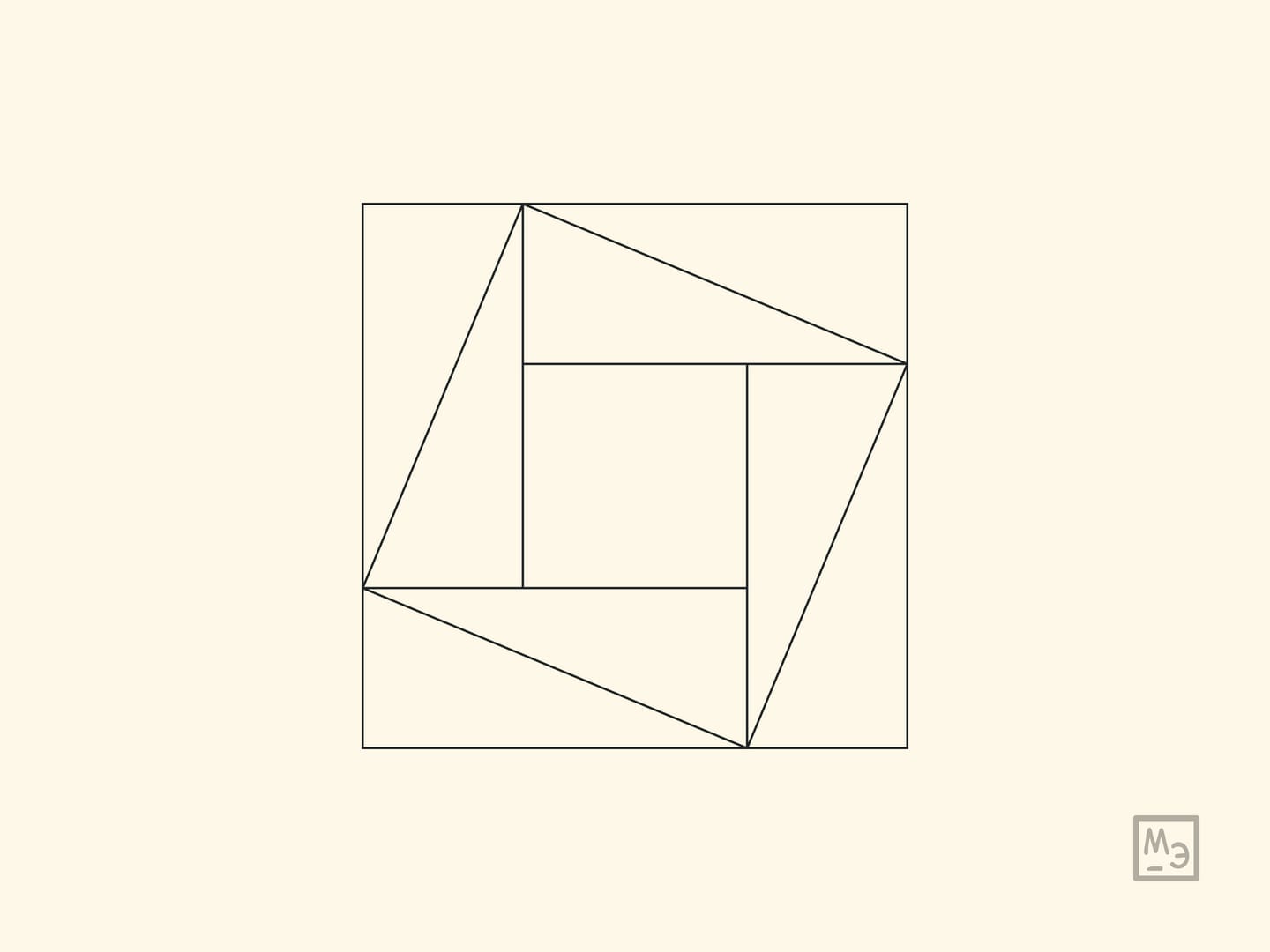
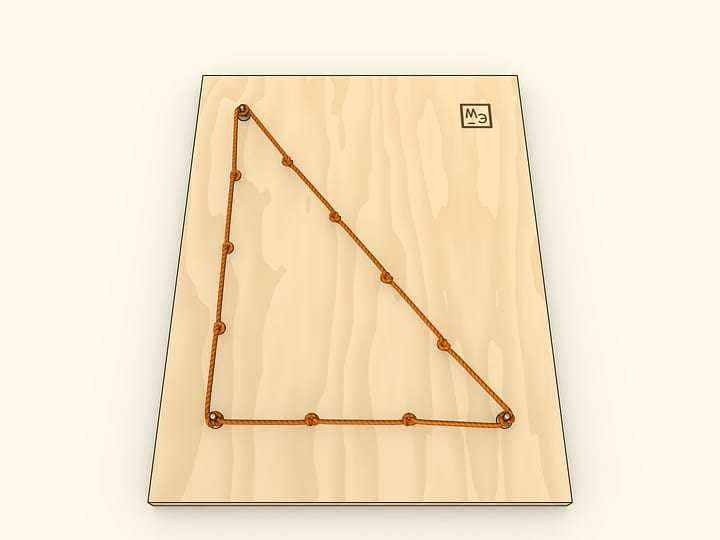
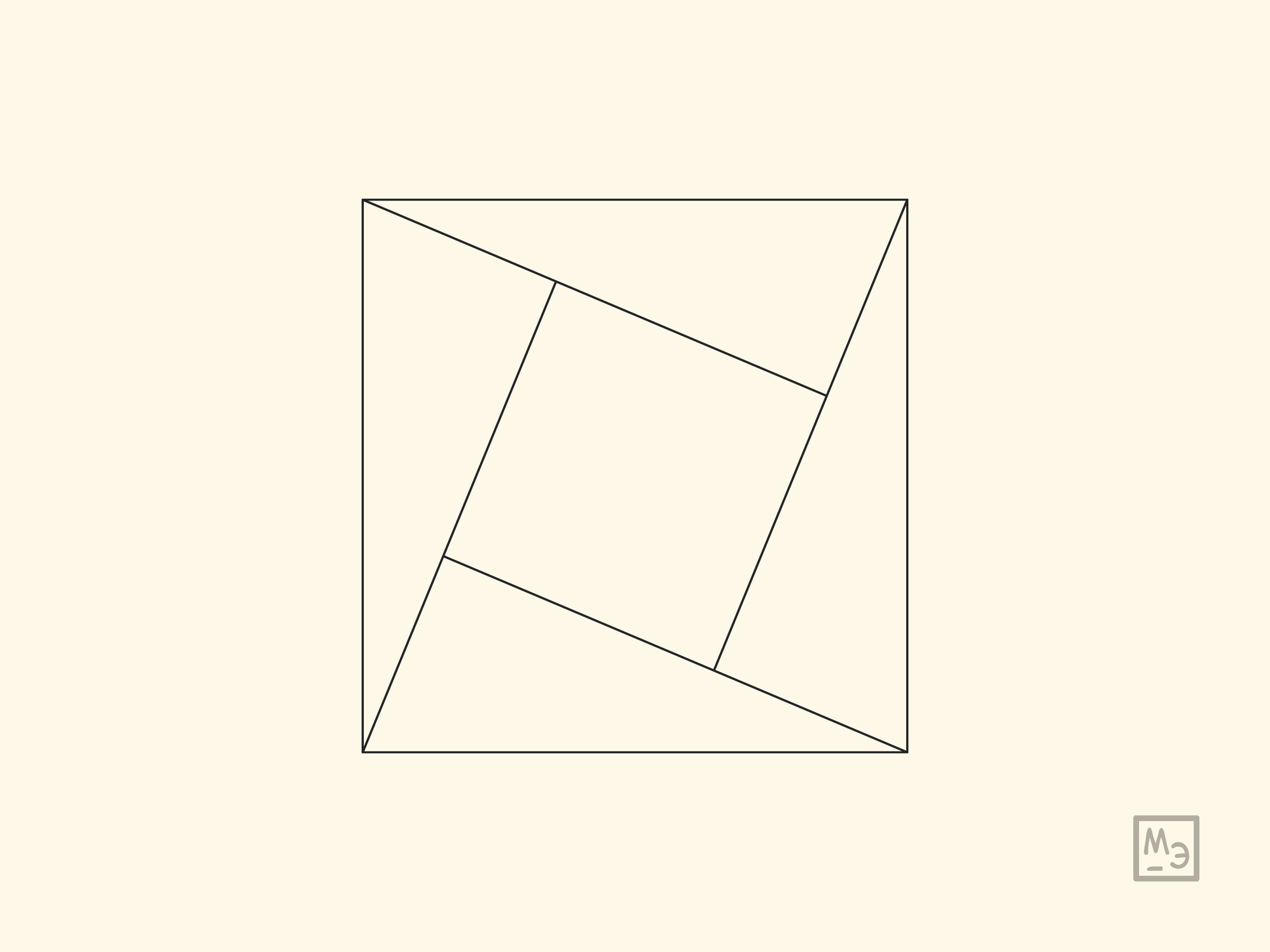
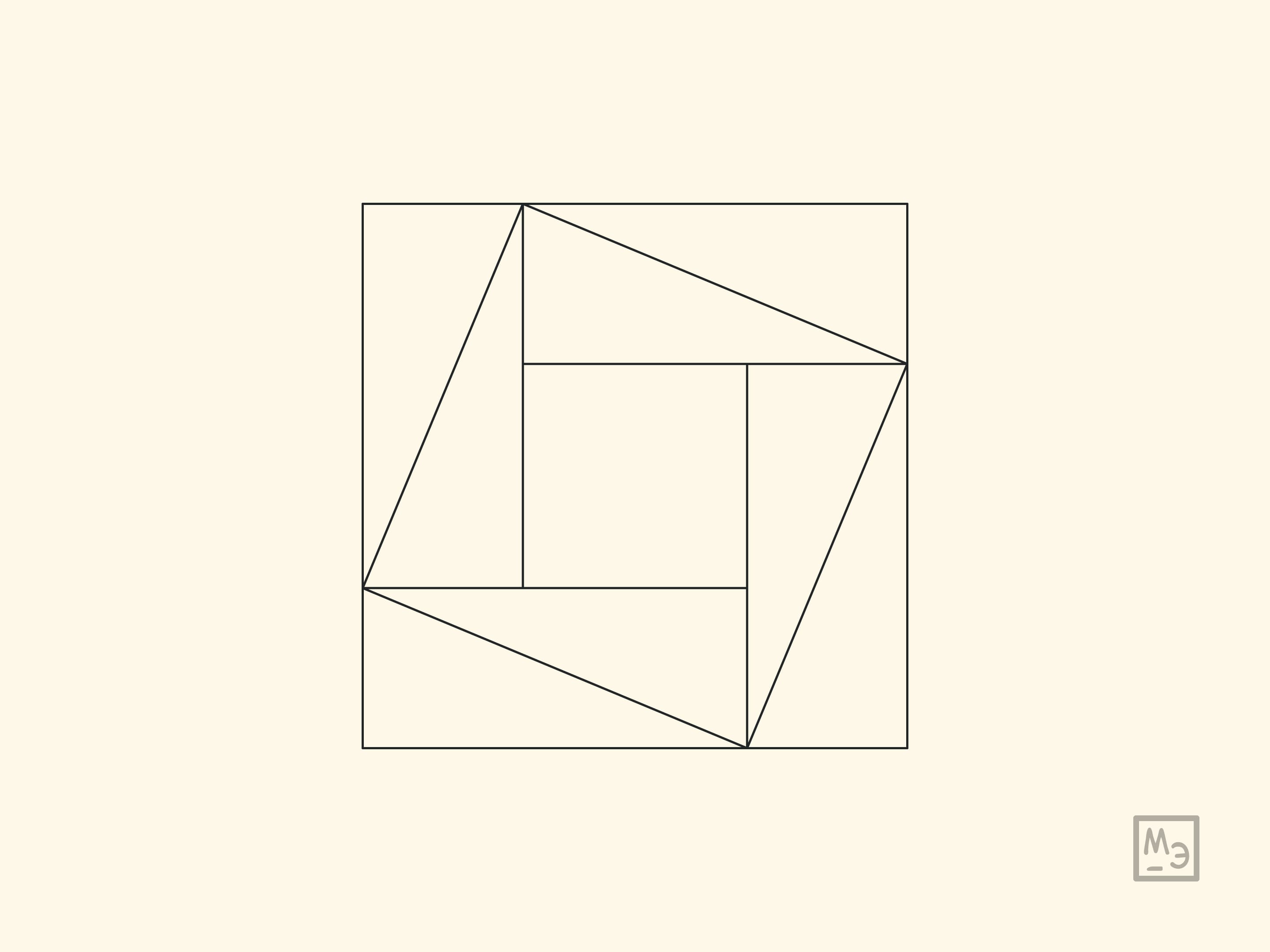
Подоб­ные дока­за­тельства известны с древ­но­сти. В древ­не­ки­тайском «Трак­тате об изме­ри­тель­ном шесте» ука­зы­ва­ется, что тео­рема Пифагора для прямо­уголь­ного тре­уголь­ника со сто­ро­нами $3$, $4$, $5$ была известна Шан Гао за 1100 лет до н. э., а в общем слу­чае — Чэнь-цзы, жившему в VI веке до н. э. В коммен­та­риях к этой книге ука­зано, что дока­за­тельство этой тео­ремы было осно­вано на чер­теже при­во­димом ниже (левый чер­тёж). А в индийской книге «Венец зна­ний» (Бхас­кара, XII век) в каче­стве дока­за­тельства тео­ремы Пифагора при­ве­дён пра­вый чер­тёж, допол­нен­ный надпи­сью «Смотри».

При­ве­дён­ные кар­тинки — лишь идеи дока­за­тельств. Рекомен­дуем вос­ста­но­вить их пол­но­стью в каж­дом слу­чае.