Как посчитать площадь под синусоидой? Более точно: площадь, между графиком функции $\sin x$ и его «основанием».
Оказывается, эту площадь можно посчитать без применения интегралов, по сути — ничего не считая! Стоит только вспомнить, что функция синуса — нечётная, т. е. $\sin (-x)=-{\sin x}$. На геометрическом языке это означает, что график функции симметричен относительно начала координат.
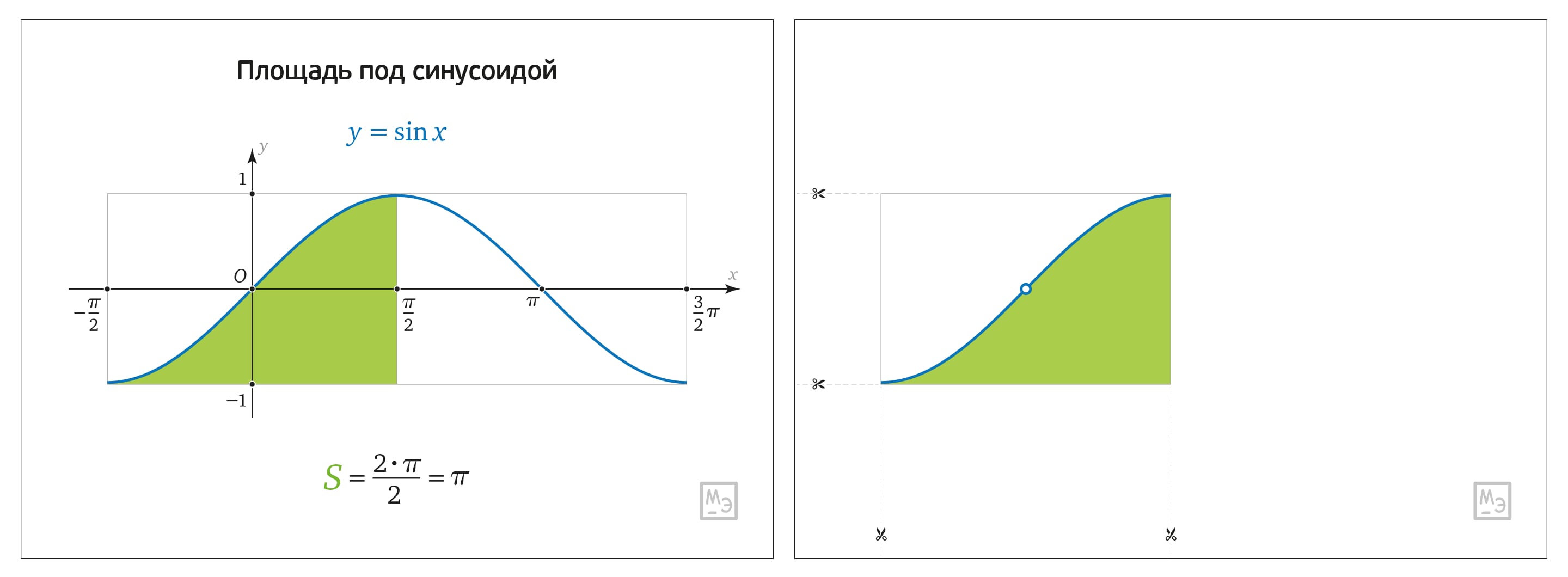
Центральная симметрия подсказывает идею модели, иллюстрирующую подсчёт площади. На листе бумаги распечатаем график синуса и закрасим под ним площадь на отрезке $[-\pi/2, \pi/2]$. На «прозрачке» повторим картинку.
Если наложить прозрачку на бумажный график, то картинки, естественно, совпадут. Воткнув канцелярскую скрепку в начало координат, повернём прозрачку на $180^\circ$. Кривая синуса совпадёт с собой! А вот закрашенным, причём без наложений, окажется уже весь прямоугольник $[-\pi/2, \pi/2]\times [-1,1]$. Посчитать площадь прямоугольника, а затем поделить пополам, — несложно.
Итак, площадь под синусом (между графиком функции $\sin x$ и его «основанием») на участке $[-\pi/2, \pi/2]$ равна $\pi$, а на полном периоде, соответственно, $2\pi$. Этот факт в совокупности с лепестками Роберваля, о которых будет отдельный сюжет, дают способ вычислить площадь под аркой циклоиды.
По сути, модель основана на том, что синусоида делит прямоугольник на две равновеликие части. Подобный трюк, очевидно, можно проводить и с другими нечётными (или сводящимися к ним) функциями.
Литература
Берман Г. Н. Циклоида. — М.: Наука, 1980. — С. 30.