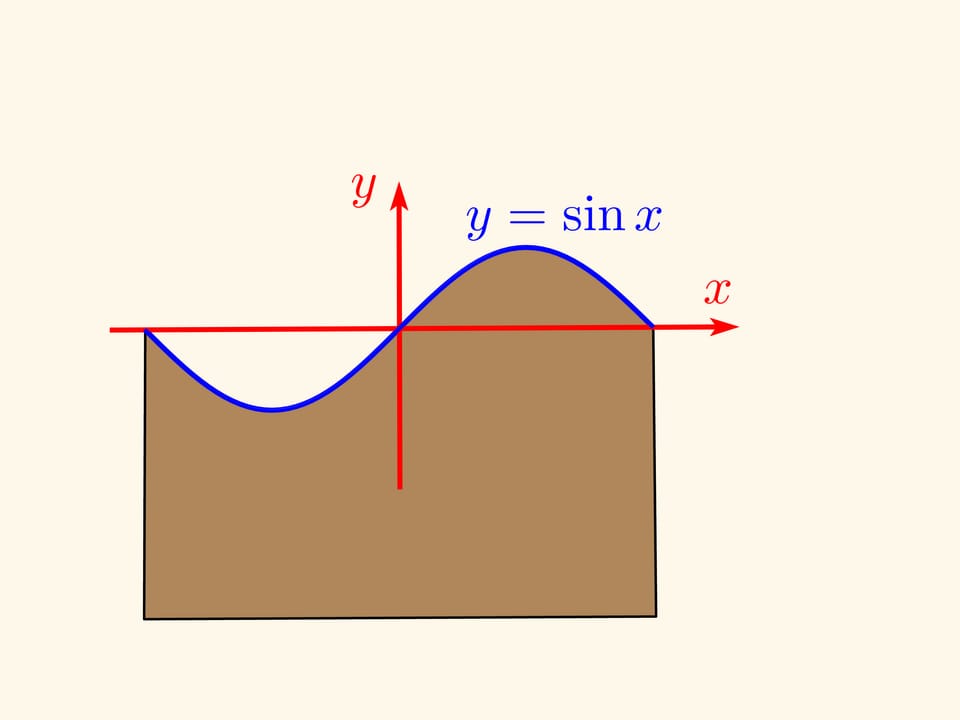
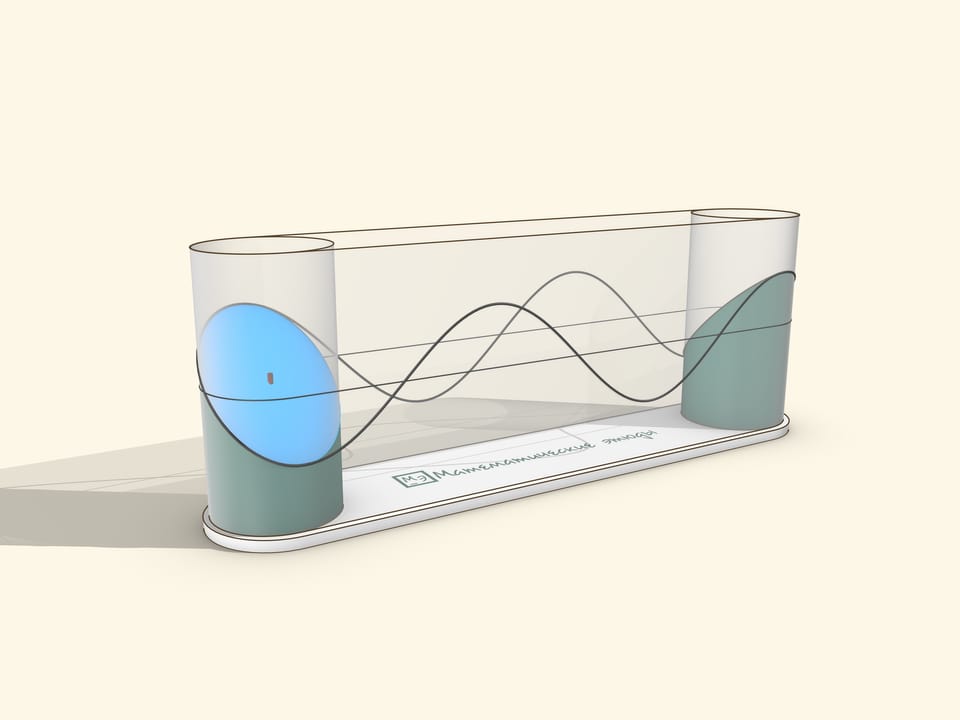
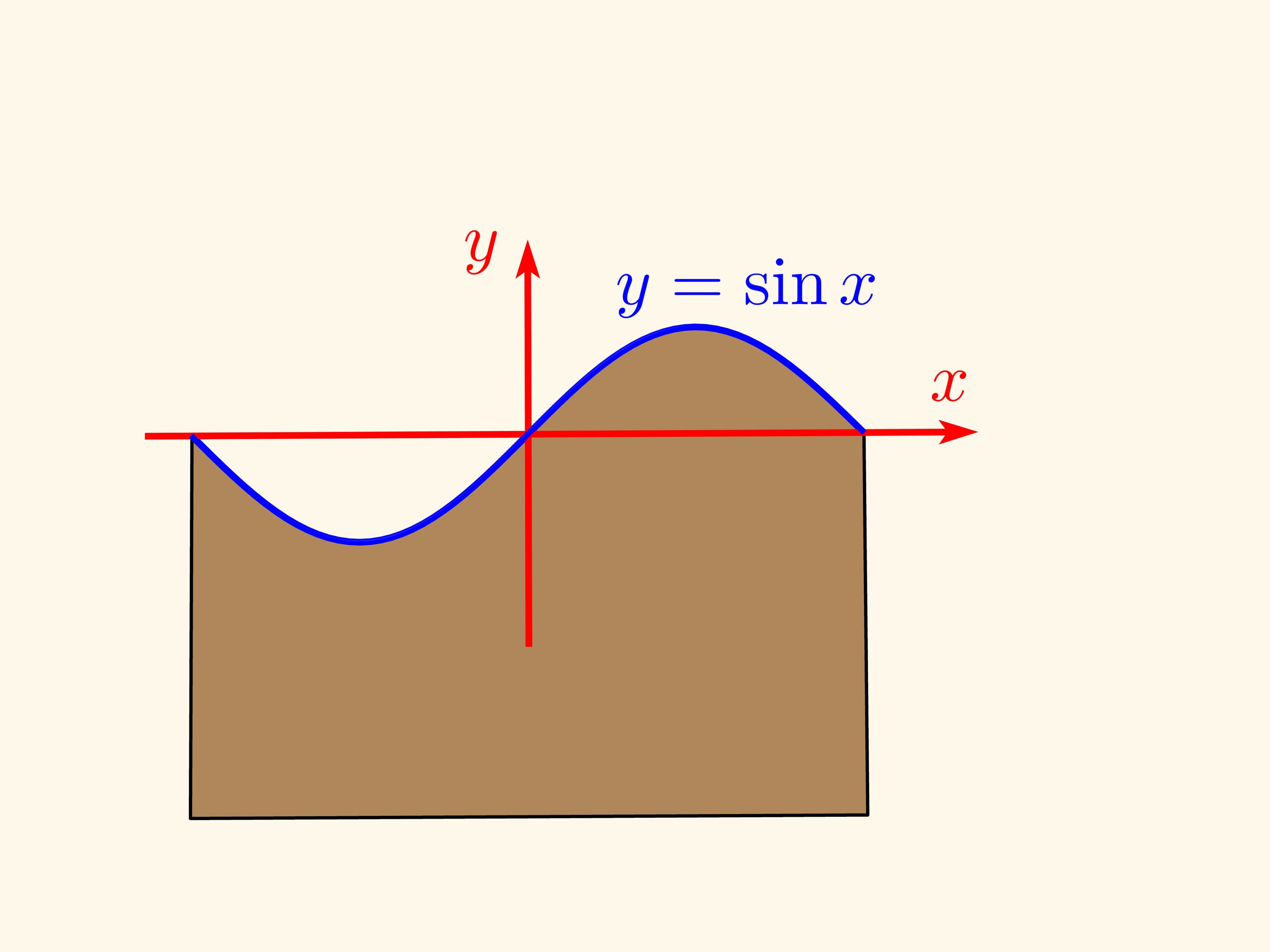
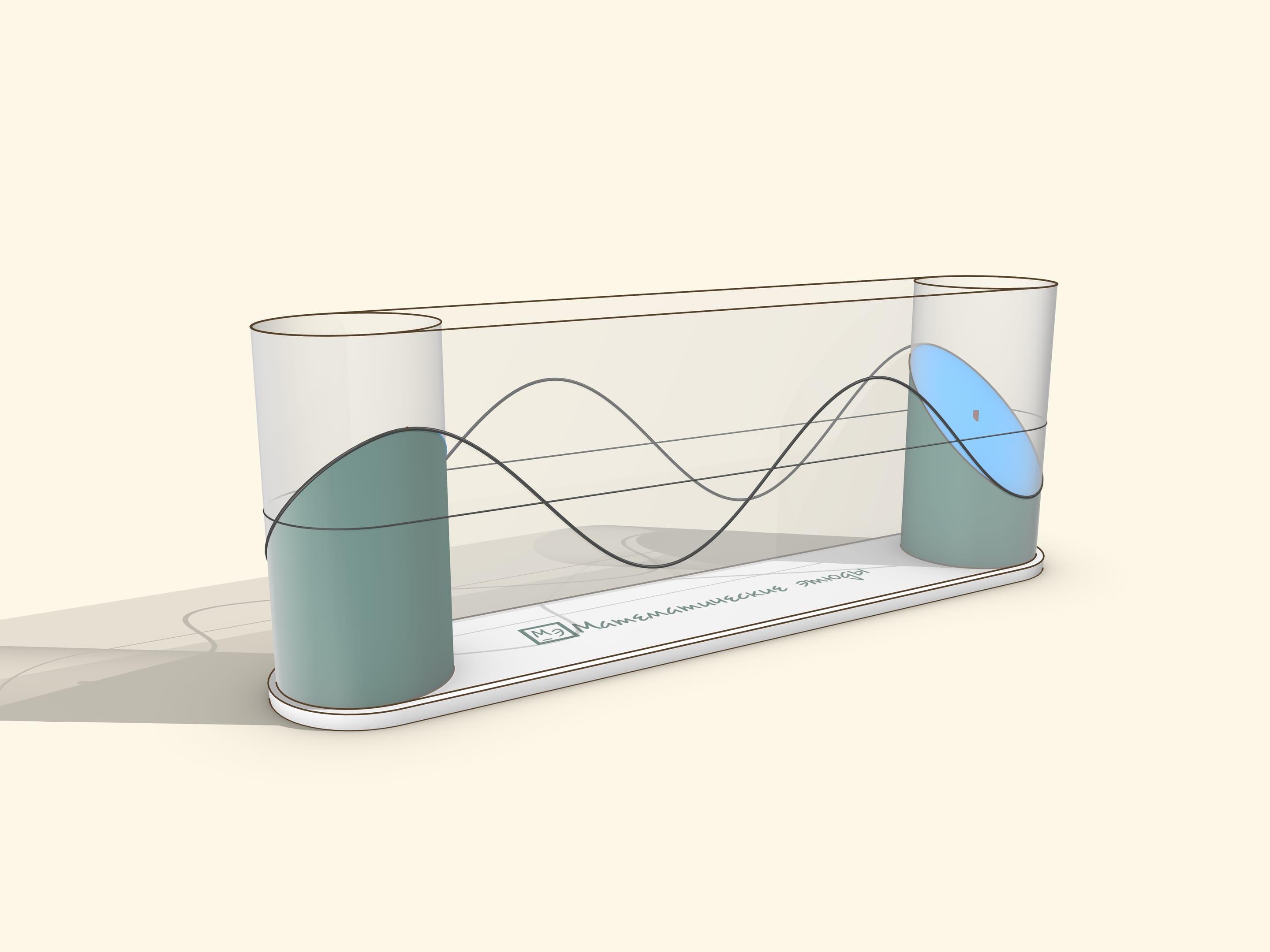
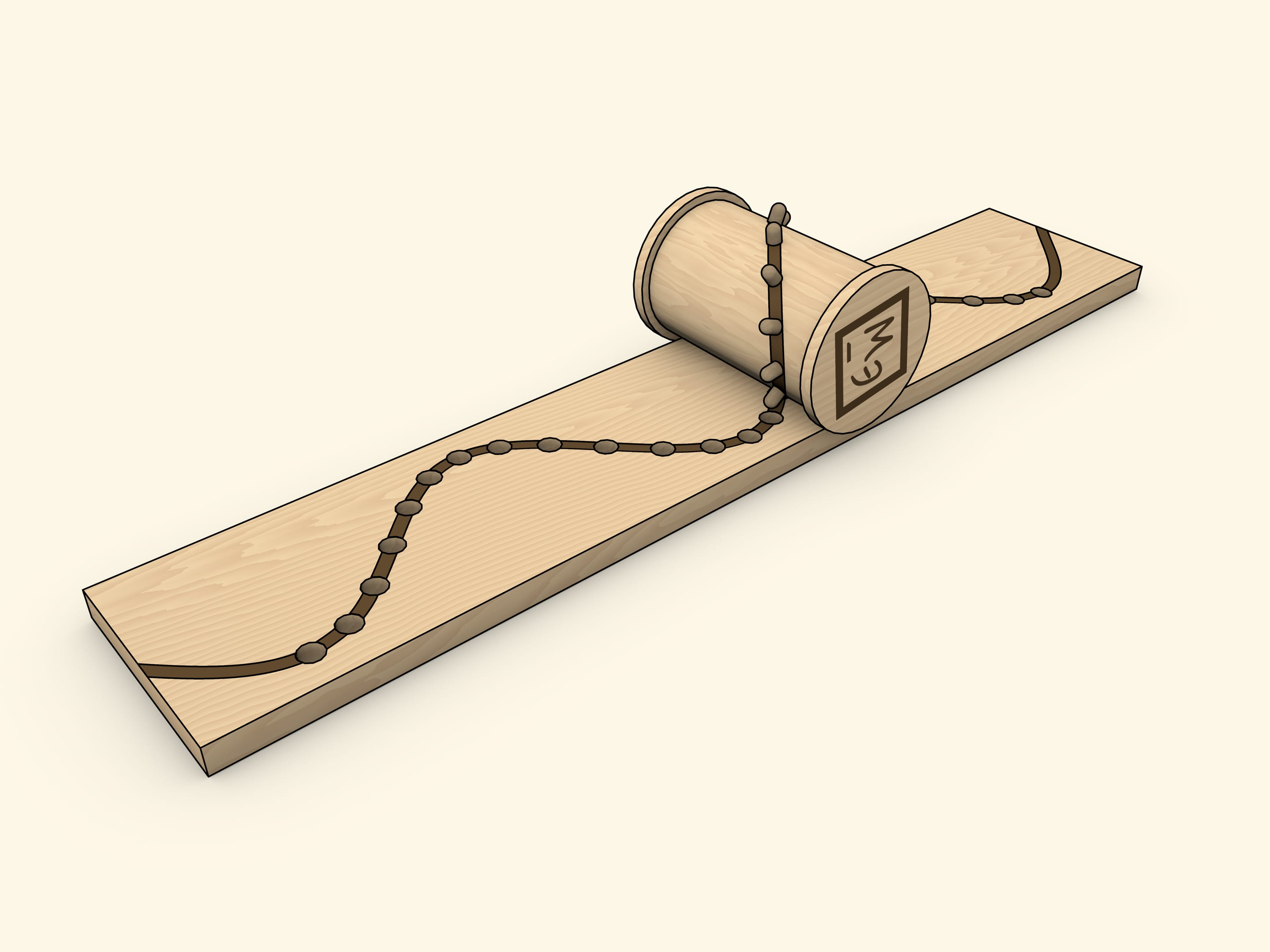
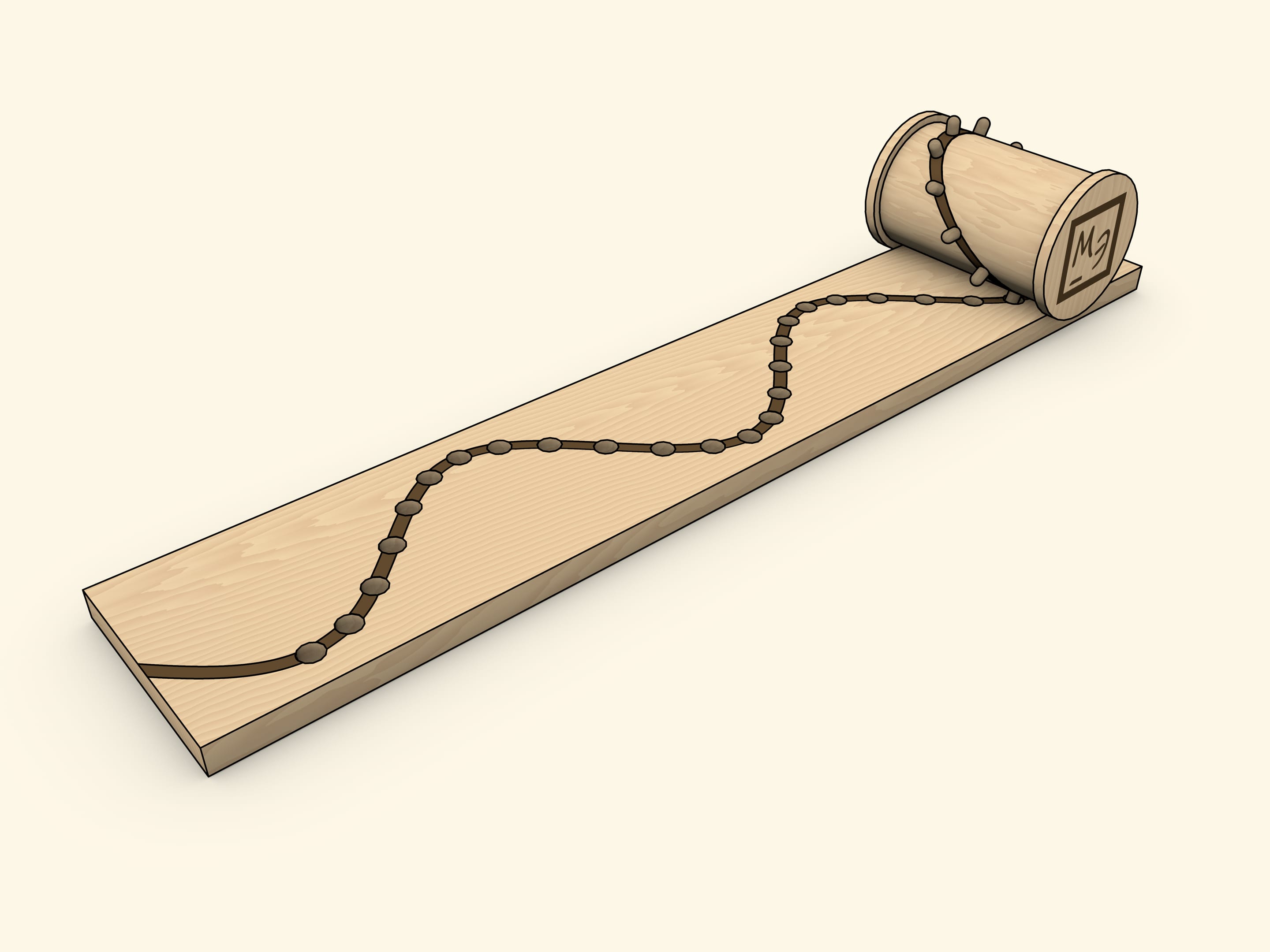
График синусоиды можно получить как развёртку «срезанного под углом» цилиндра (или, что то же самое — с нарисованным на нём эллипсом).
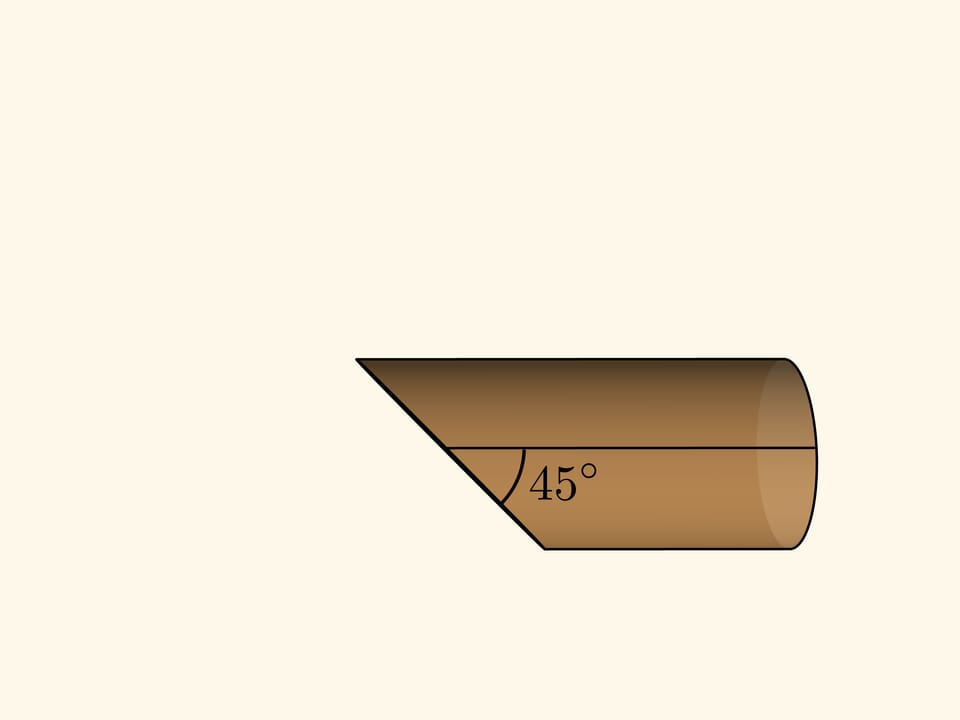
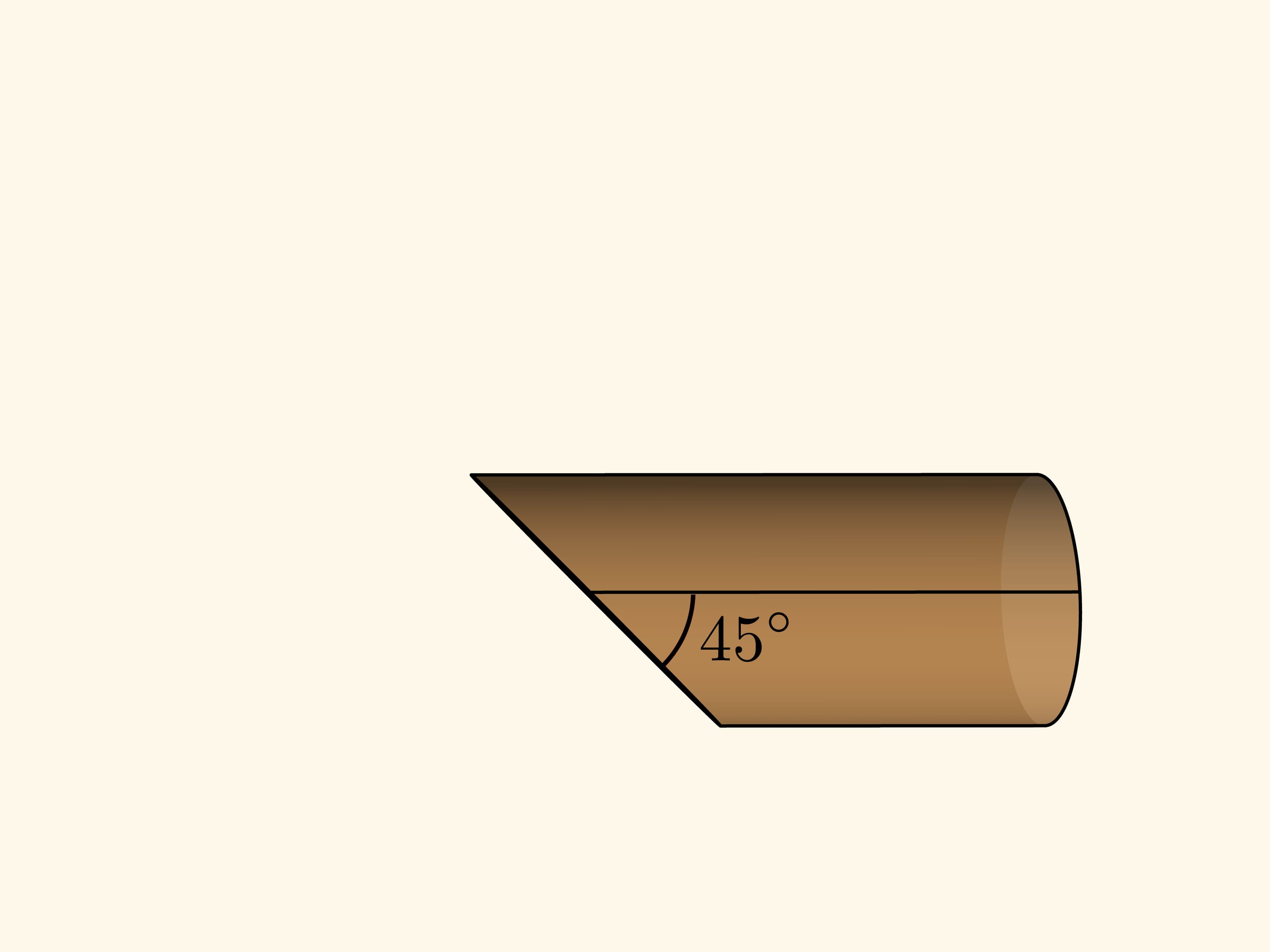
Для получения синусоиды в домашних условиях достаточно иметь батон колбасы. Как известно, колбасу надо резать под углом — тогда куски больше.
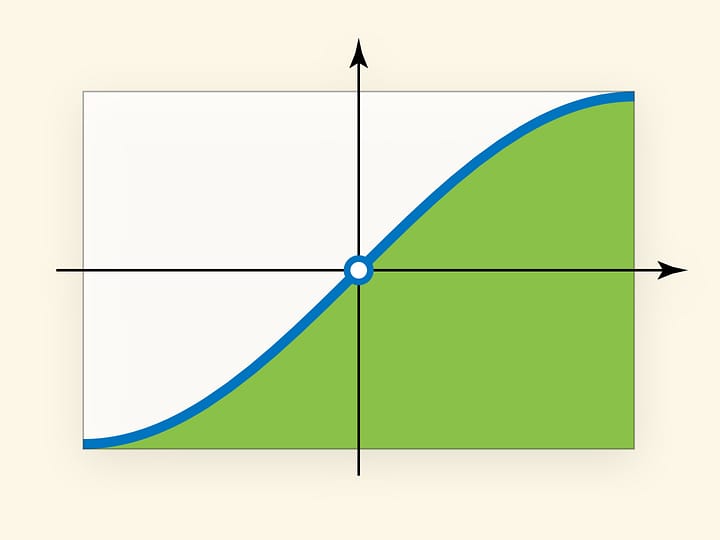
Надрежем шкурку вдоль ещё непорезанной части колбасы и развернём шкурку на плоскость. Если сечение было проведено под углом 45 градусов к оси цилиндра (примем его радиус за единицу), то один край шкурки (развёртки цилиндра) будет в точности синусоидой — графиком функции $y=\sin x$! Если же угол был произвольным, $\alpha ,$ то получится сжатый график $y=\tg\alpha \sin x $.
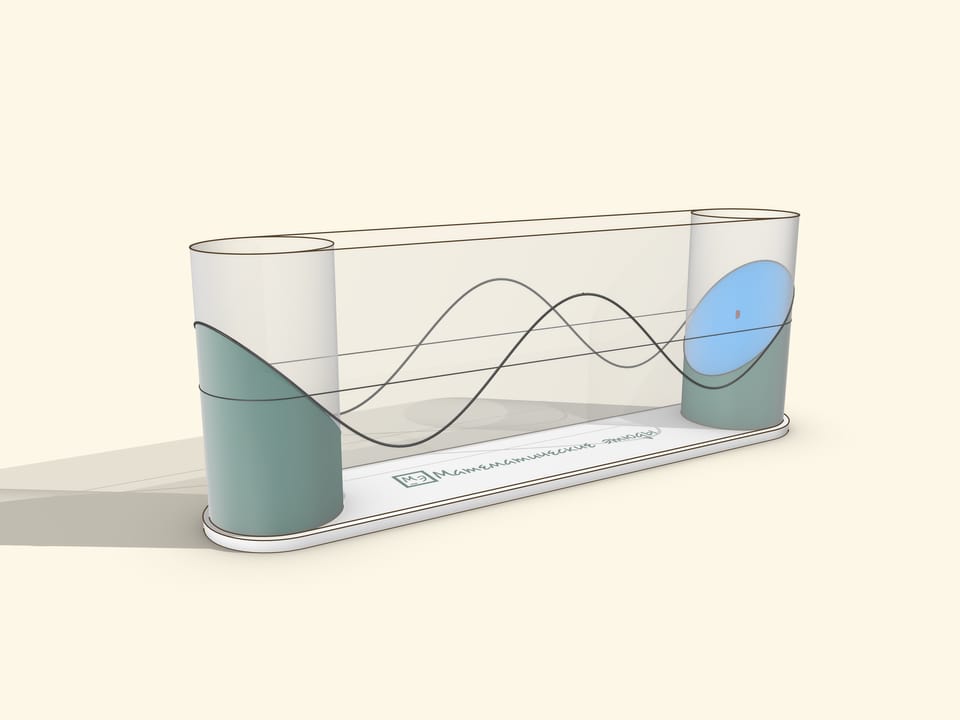
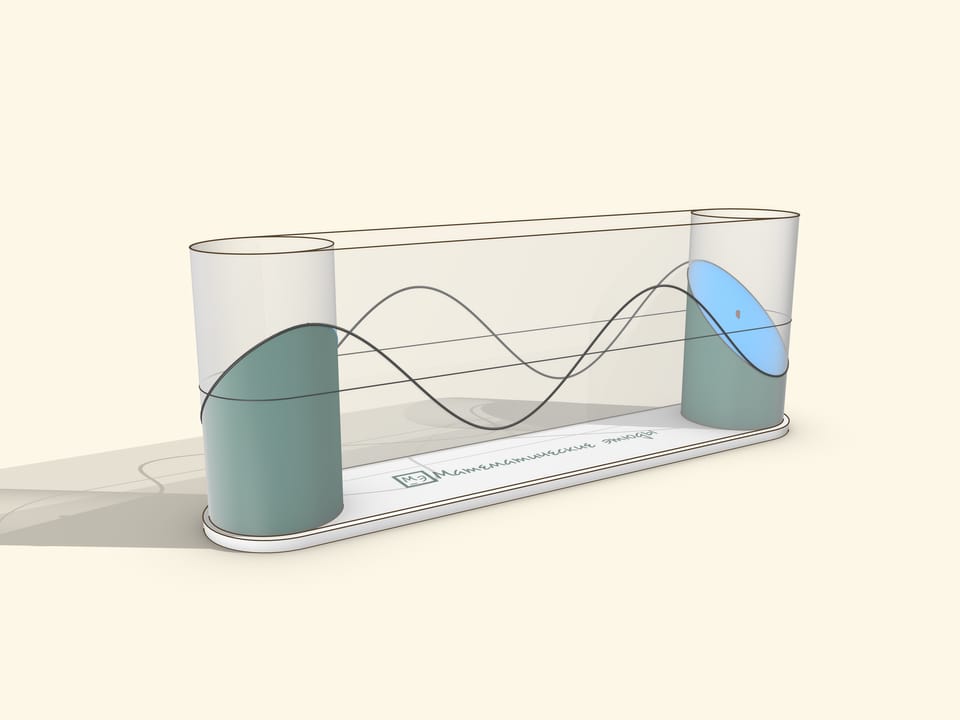
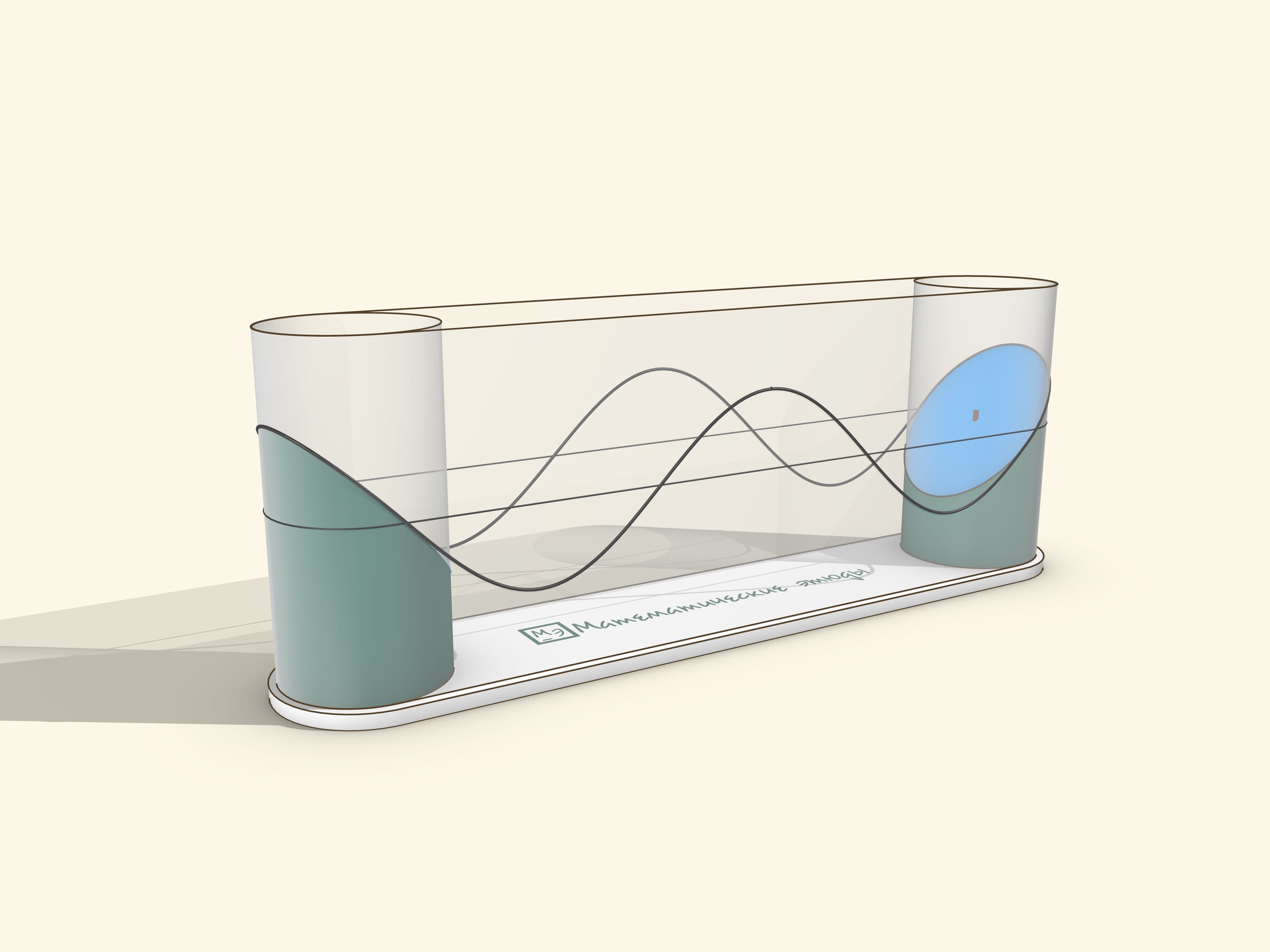
Музейный экспонат можно сделать натянув прозрачную плёнку на два цилиндра. Привод стоит делать ручным, чтобы пользователь мог вращать с удобной ему для наблюдения скоростью и останавливать для созерцания, как синусоида сматывается с цилиндра.
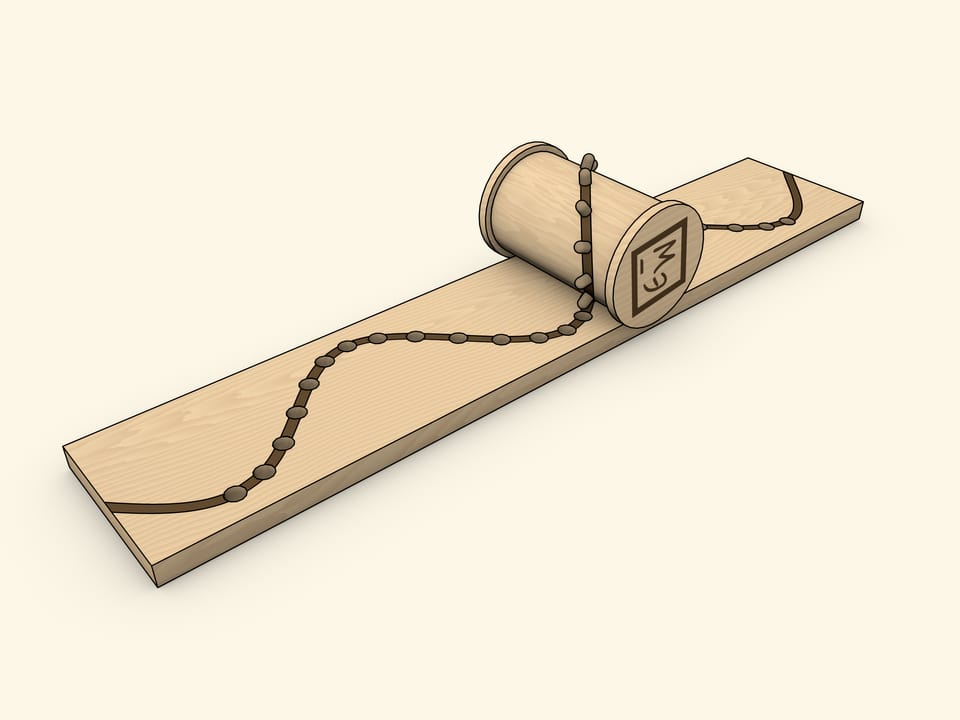
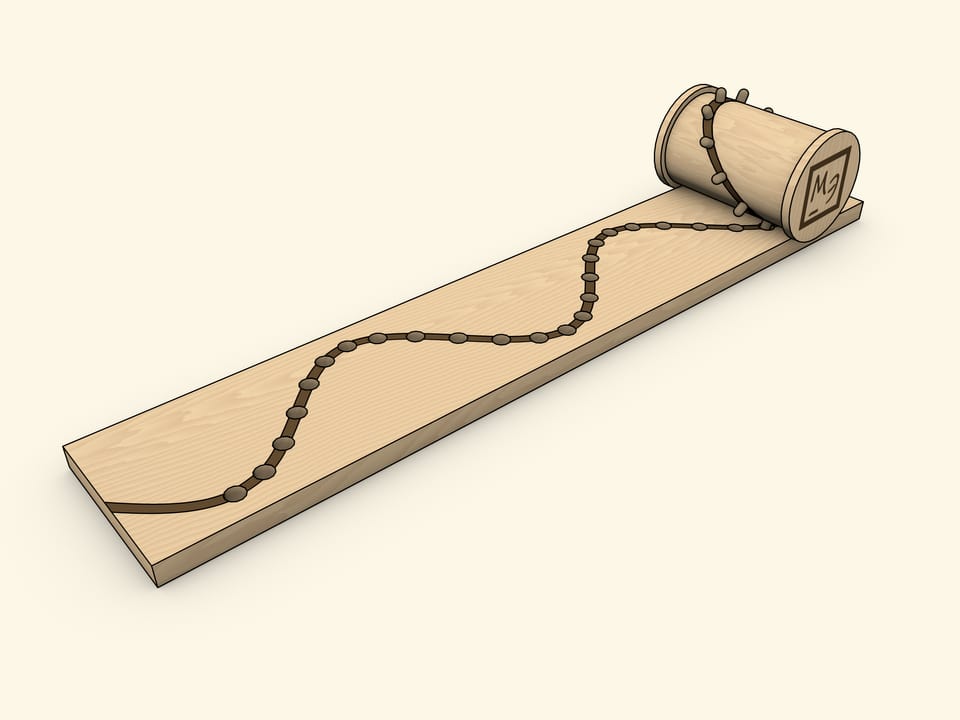
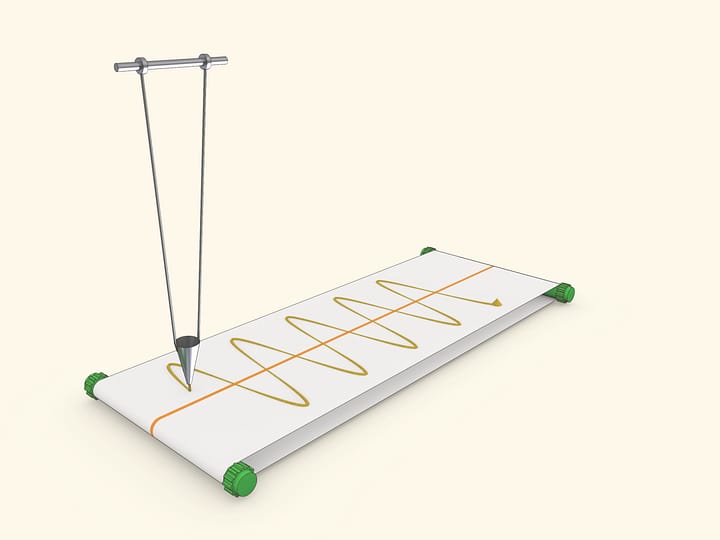
Ещё один «домашний» способ получения синусоиды как развёртки цилиндра — катушка со вставленными вдоль эллипса штырьками.
Выбор катушки неслучаен: реборда при правильно подогнанной ширине основания позволяет избежать перекосов. При такой реализации отверстия в основании необходимо делать конусообразными и/или шире штырьков, так как они должны беспрепятственно входить и выходить «под углом».