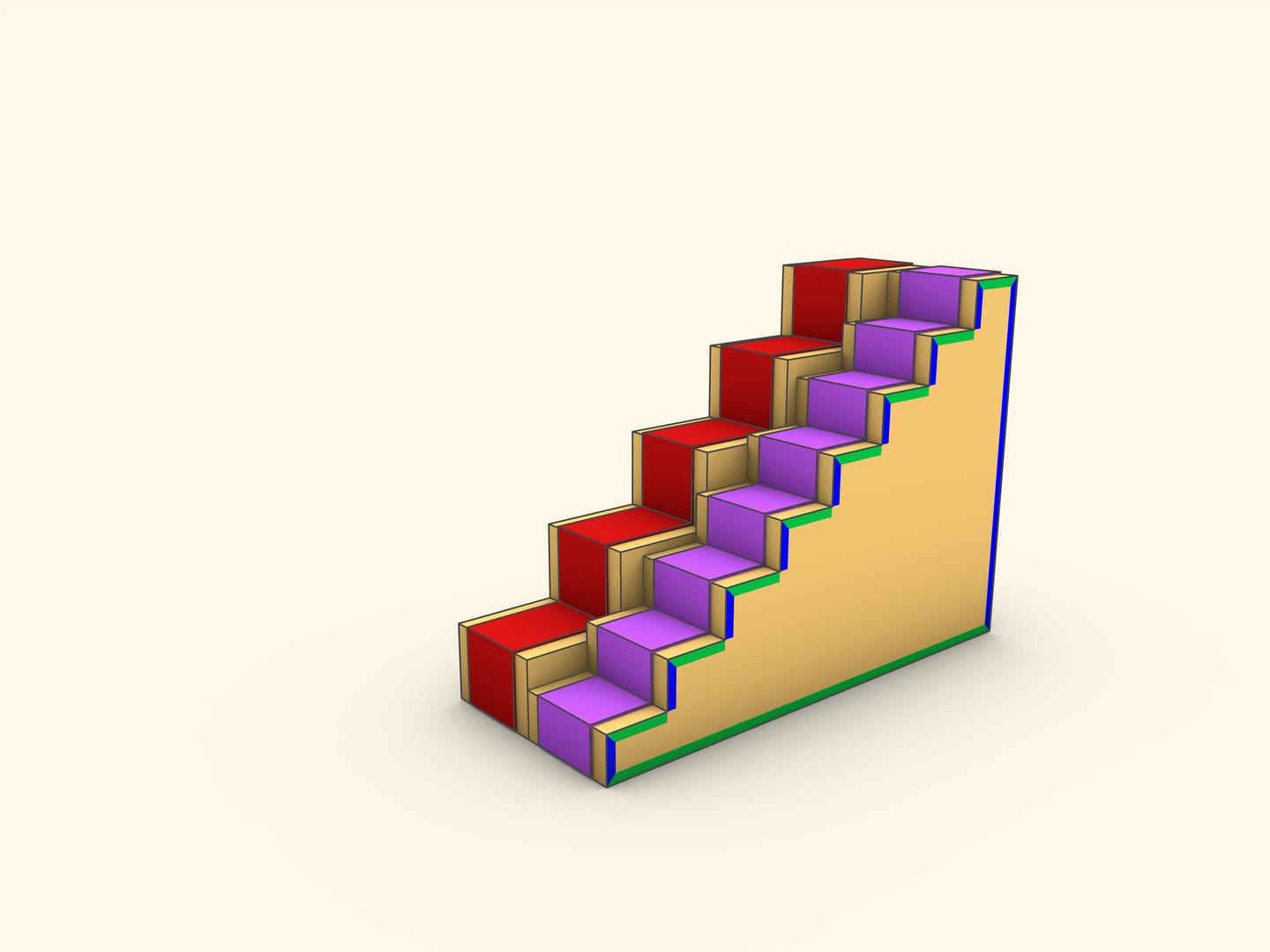
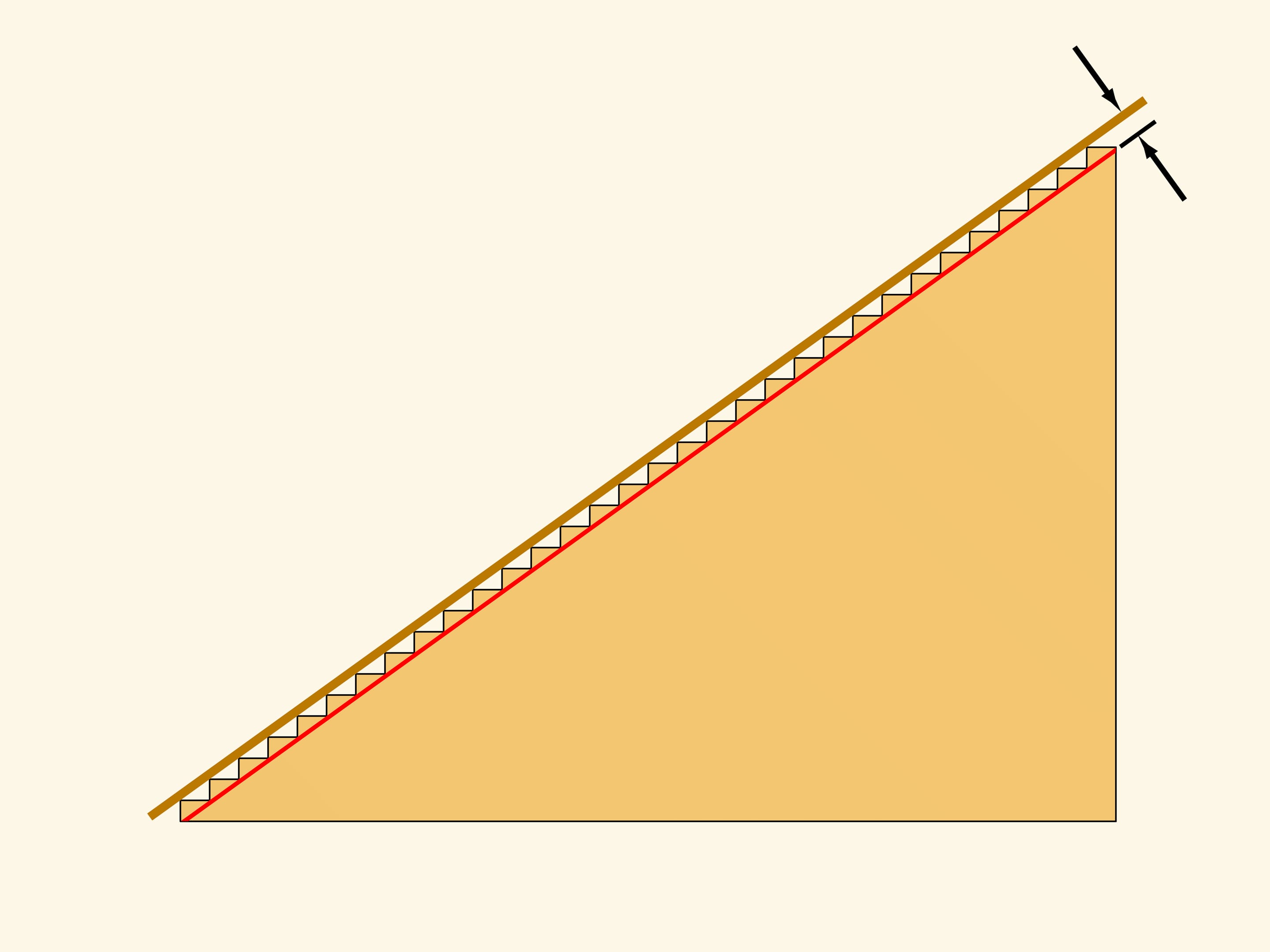
Рассмотрим две лестницы с общим началом и приходящие в одну и ту же точку, но с разными количествами ступенек. Классическая детская задача: у какой из лестниц длина больше — где ступеньки мельче или крупнее? Для какой из лестниц потребуется более длинная ковровая дорожка?
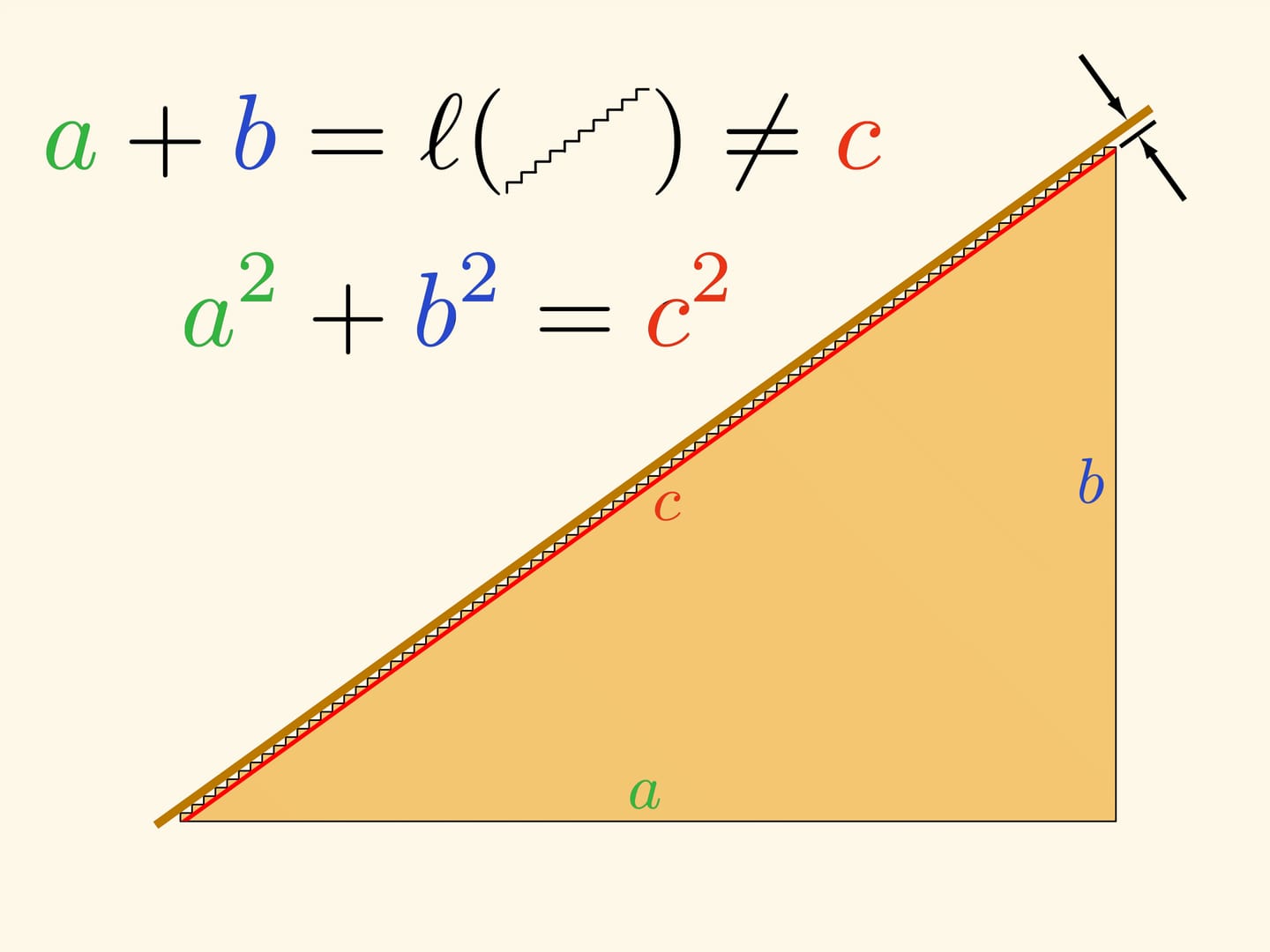
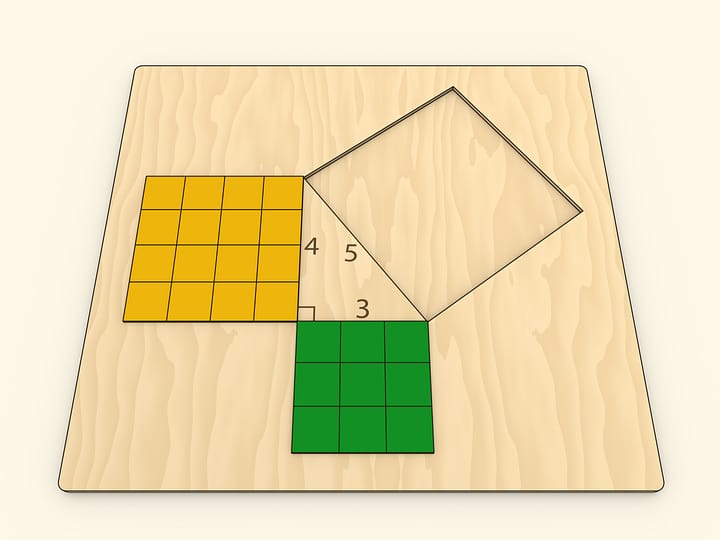
Несложно доказать, что длина ковровой дорожки не зависит от размера ступеней. Достроим лестницы до прямоугольного треугольника. Сумма длин вертикальных участков ковра равна длине вертикального катета этого прямоугольного треугольника, горизонтальных — горизонтального. Таким образом, длина всей ковровой дорожки равна сумме катетов, которая не зависит от размера ступеней.
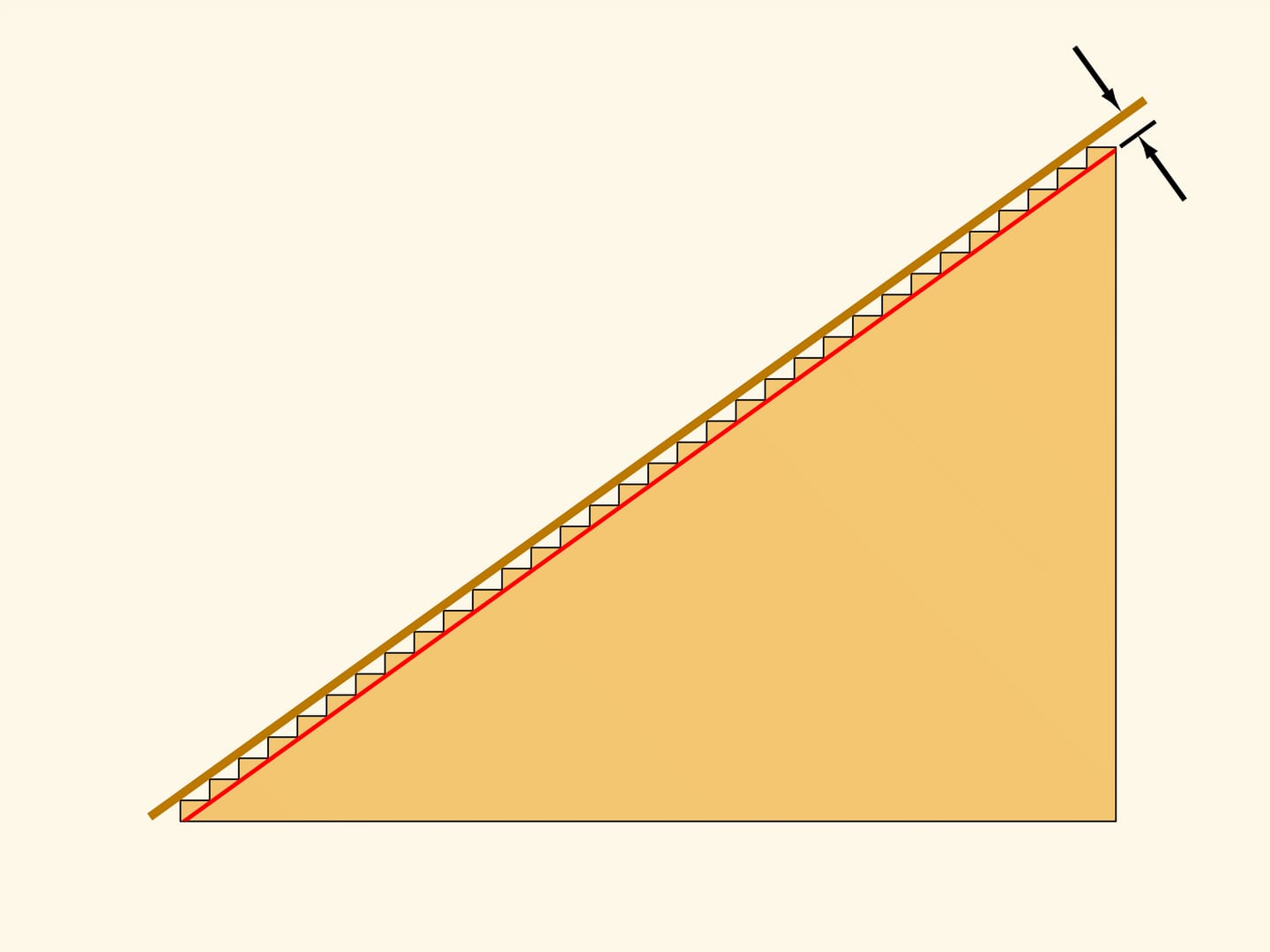
Будем делать ступени всё более мелкими. Для любой такой лестницы её длина равна сумме катетов. А лестница всё ближе и ближе к гипотенузе прямоугольного треугольника.
Очевидно, что «в пределе» получим, что длина ковровой дорожки — длина гипотенузы — равна сумме катетов, т. е. $c=a+b$… Но постойте, мы ведь с вами хорошо знаем теорему Пифагора, говорящую, что $c^2=a^2+b^2$! А это совсем не то же самое, что $c=a+b$…
За словами «очевидно, что» часто кроются ошибки — старайтесь их не употреблять в математических текстах. А чтобы запомнить это, попробуйте разобраться, в чём же была допущена ошибка.
Литература
Далёкое близкое // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 69—69, 314—315.