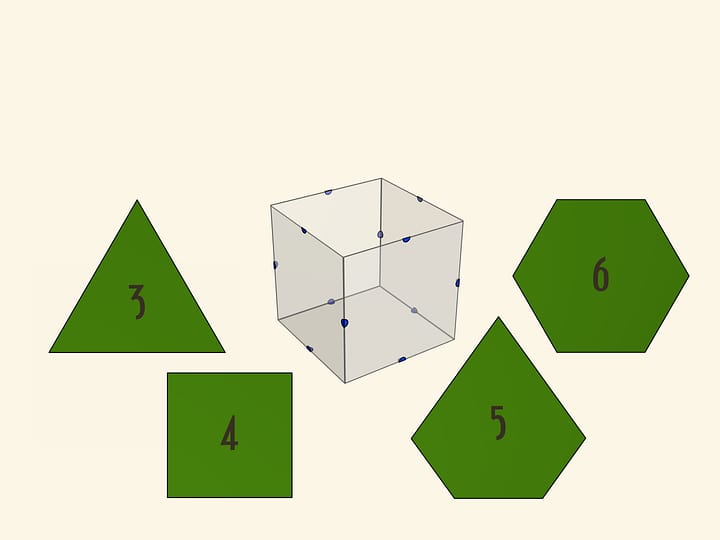
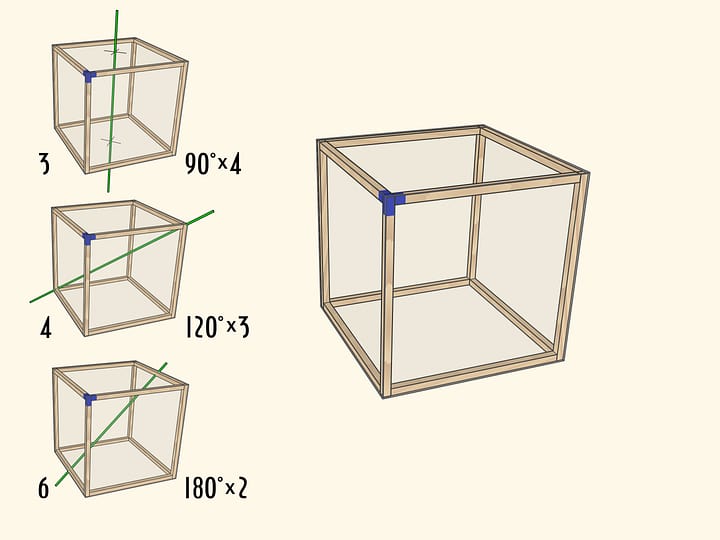
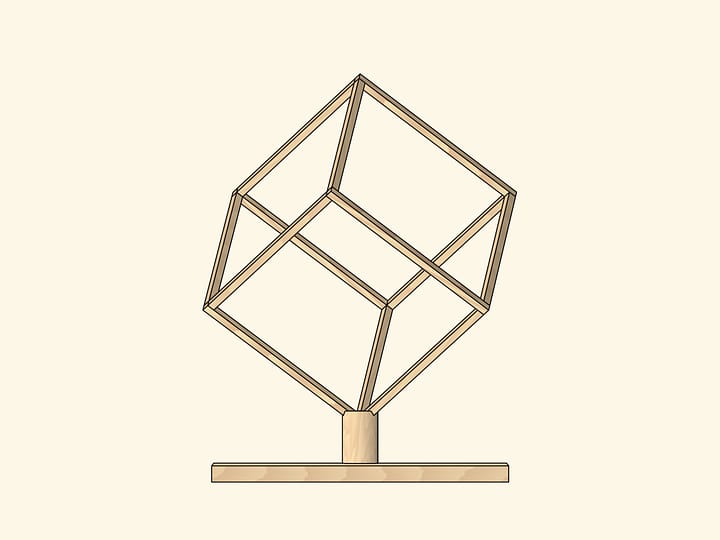
Пять правильных многогранников — тетраэдр, октаэдр, куб, икосаэдр и додекаэдр — красиво вписываются друг в друга. Например, тетраэдр можно вписать в додекаэдр. Более того, вершины додекаэдра можно так покрасить в $5$ цветов, что вершины каждого цвета образуют правильный тетраэдр! А значит, можно сделать разноцветную модель одной из 59 звёздчатых форм икосаэдра.
Поворотов, переводящий додекаэдр в себя, $12\cdot5=60$ штук: додекаэдр можно поставить на любую из 12 граней и в таком положении повернуть 5 способами. Каждый поворот как-то переставляет рассматриваемые $5$ тетраэдров. Оказывается, что вращение додекаэдра полностью определяется тем, как оно переставляет тетраэдры. Но из вращений додекаэдра происходят не все $5!=120$ потенциально возможных перестановок, а только половина — так называемые чётные перестановки. (На языке теории групп можно сказать, что возникает изоморфизм группы вращений додекаэдра с группой $A_5$ чётных перестановок.)
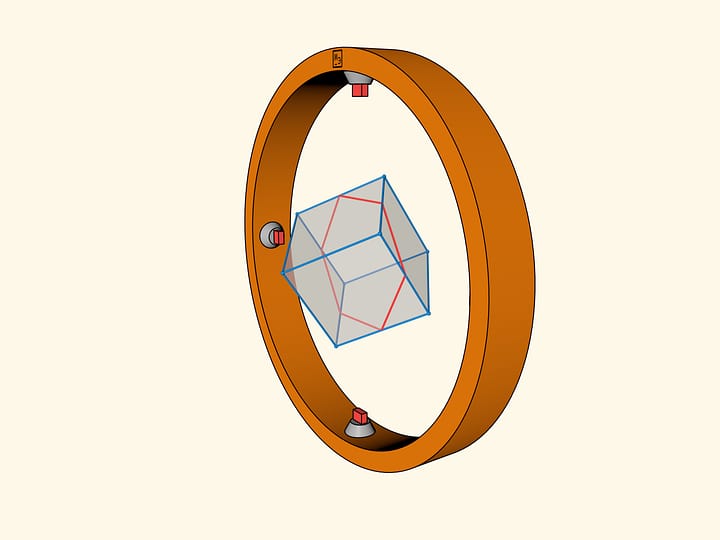
Ту же связь вращений додекаэдра с перестановками можно получить и вписывая в додекаэдр не $5$ тетраэдров, а $5$ кубов («кубы Кеплера»). При этом каждый из рассмотренных тетраэдров вписан в один из кубов Кеплера.
В куб тетраэдр можно вписать двумя разными способами. Если в каждом кубе Кеплера заменить тетраэдр на «противоположный», то получившаяся из пяти «новых» тетраэдров фигура не будет совмещаться с исходной поворотом, а только зеркальной симметрией.
Литература
Венниджер М. Модели многогранников. — М.: Мир, 1974. — Стр. 51—54.
Другие модели раздела «Многогранники»
