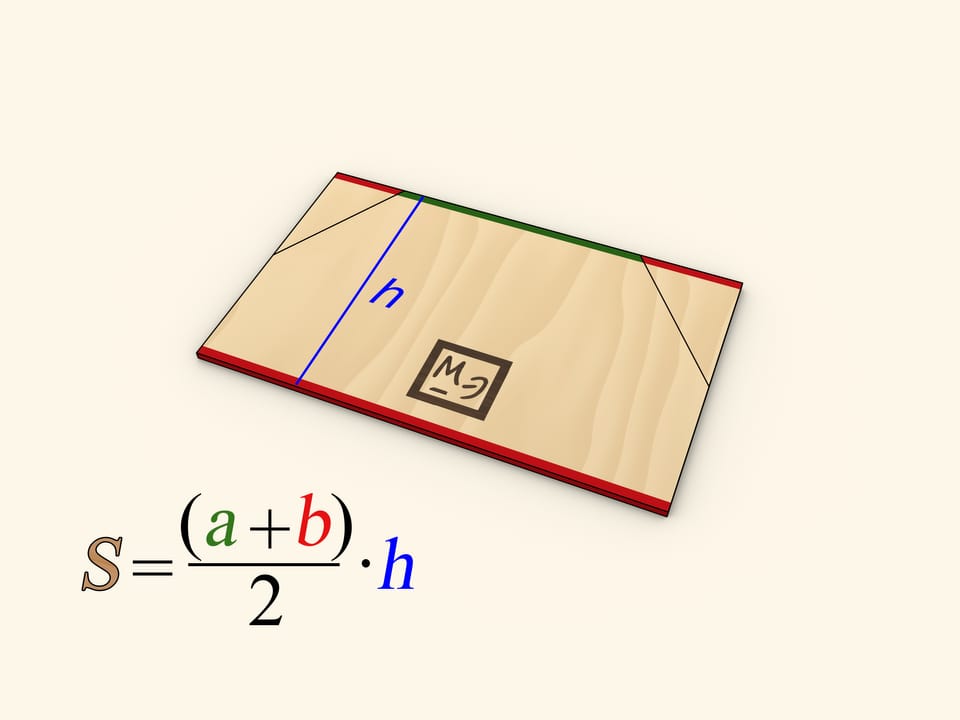
Площадь трапеции равна произведению полусуммы длин оснований на длину высоты. Более формально: если длины оснований равны $a$ и $b$, а высоты – $h$, то площадь равна $S=(a+b)/2\cdot h$. Проиллюстрировать эту формулу, а, если она забыта, вывести, можно воспользовавшись формулами вычисления площади прямоугольника или треугольника.
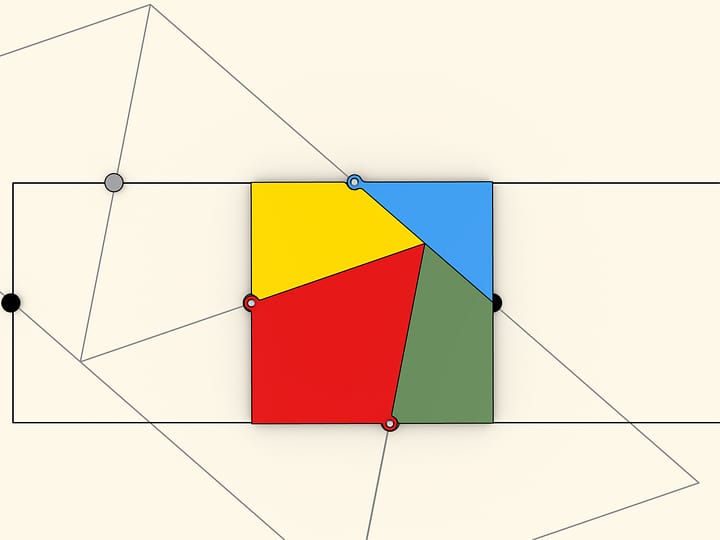
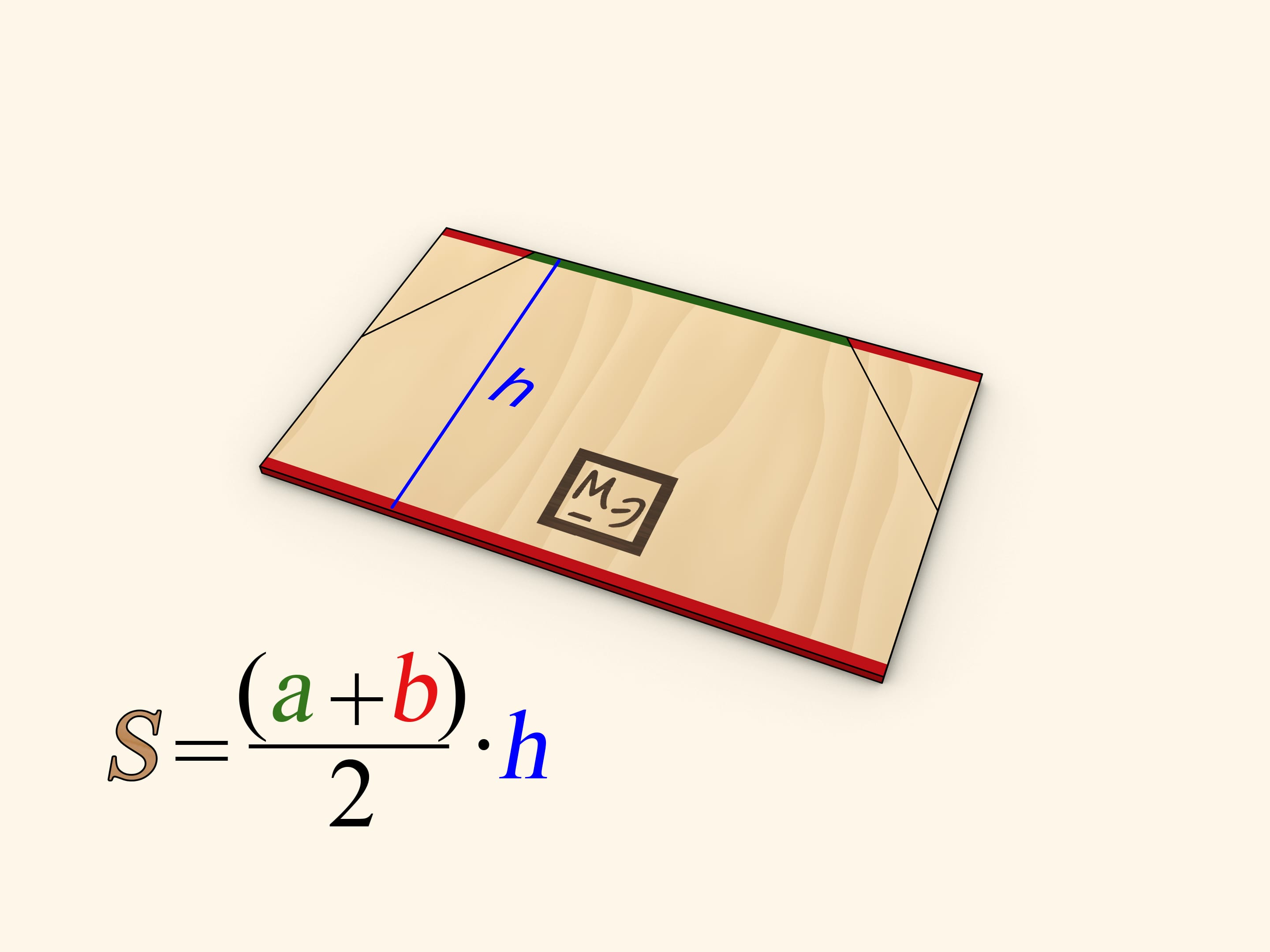
Чтобы воспользоваться формулой площади прямоугольника проведём из середин боковых сторон трапеции перпендикуляры на длинное основание и разрежем вдоль них трапецию. Отрезанные два прямоугольных треугольника приложим гипотенузами к оставшимся частям боковых сторон. Полученная фигура является прямоугольником.
Длина одной пары сторон прямоугольника совпадает с длиной высоты трапеции. Сумма длин двух других сторон равна сумме длин оснований трапеции, а, значит, длина одной стороны равна полусумме длин оснований, то есть $(a+b)/2$. Таким образом, площадь прямоугольника, а значит и площадь исходной трапеции, равна $S=(a+b)/2\cdot h$.
Для полного доказательства следует ещё убедиться, что получившаяся после перекладывания треугольников фигура в действительности является прямоугольником — каждая боковая сторона и составное основание являются прямыми линиями, а соответствующие стороны параллельны друг другу. Прямоугольность же углов заложена в самом способе разрезания — по перпендикулярам к основанию.
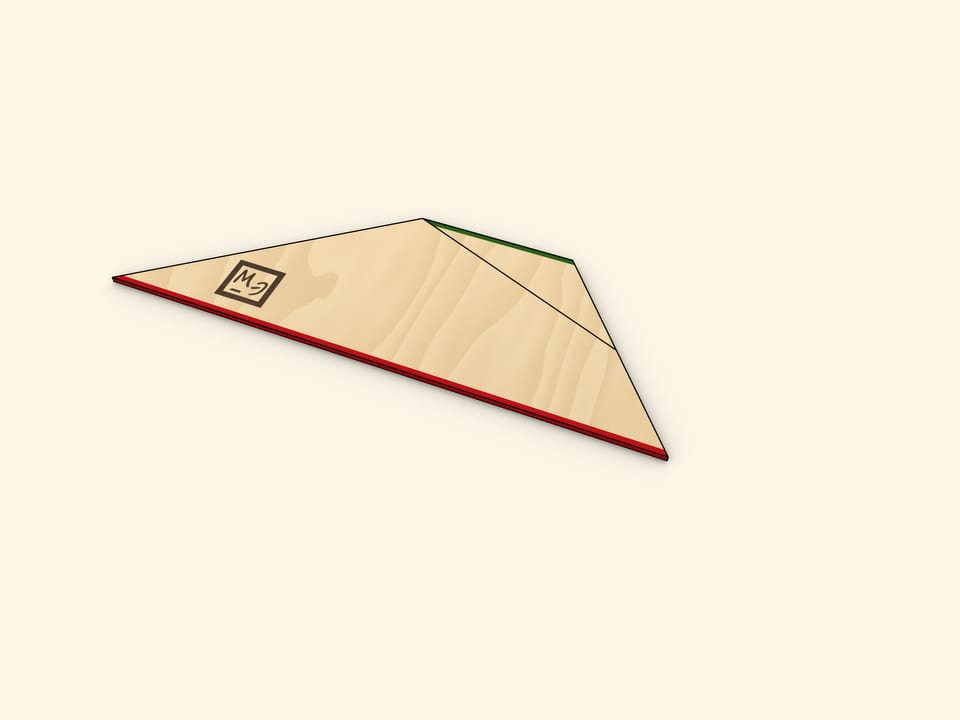
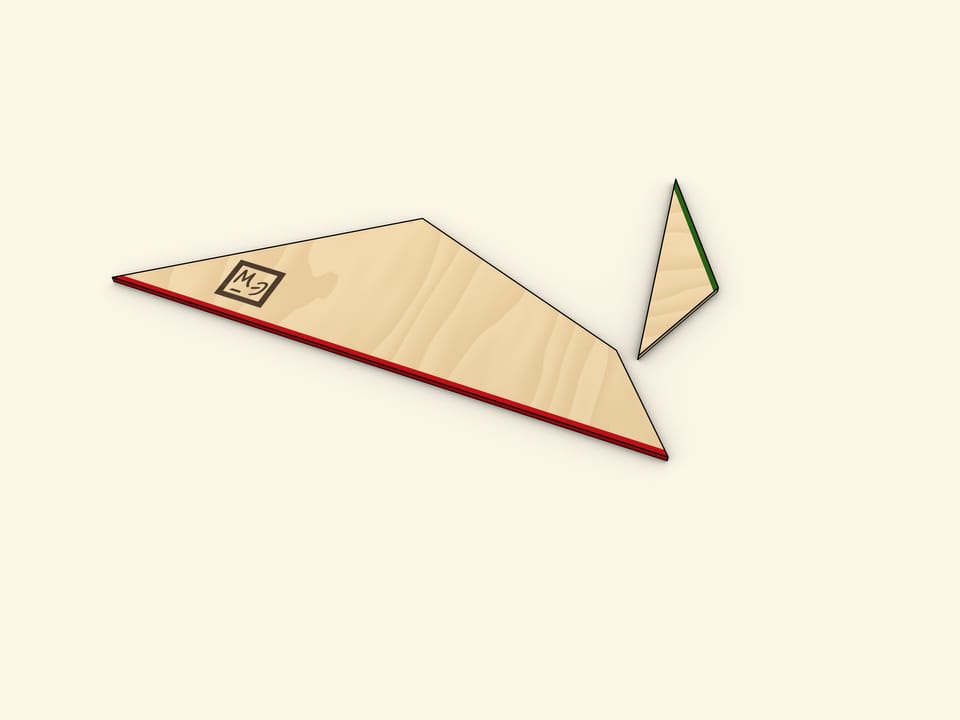
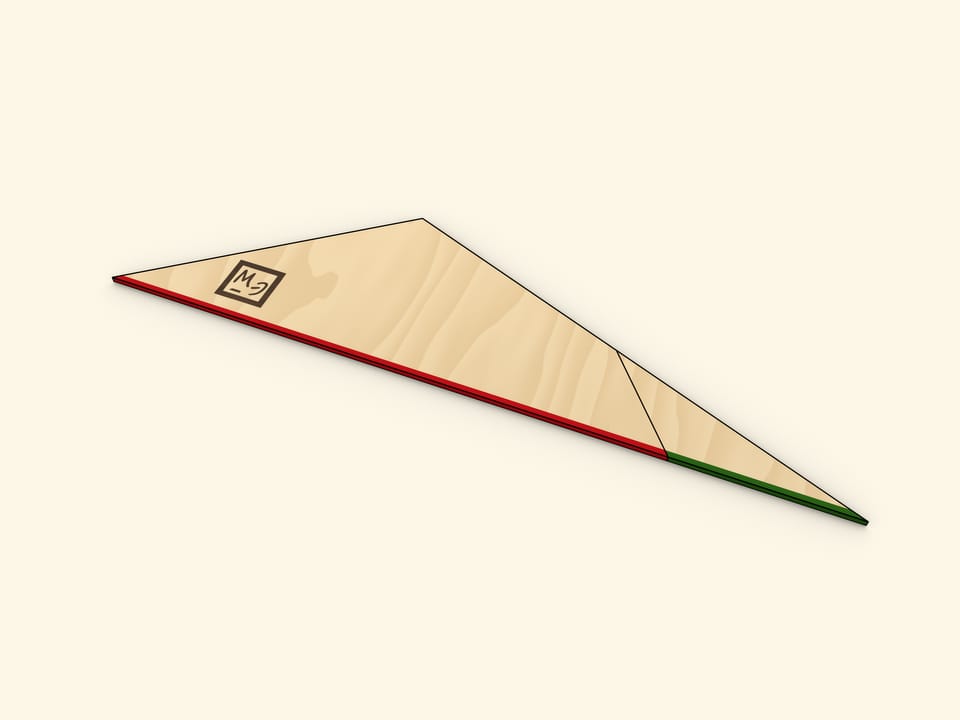
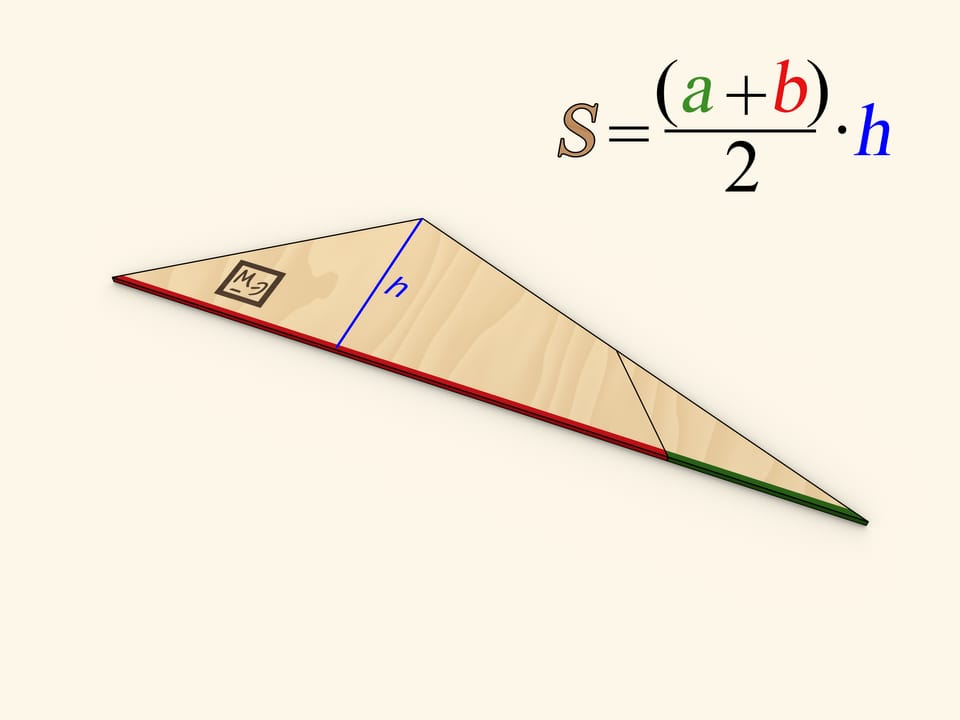
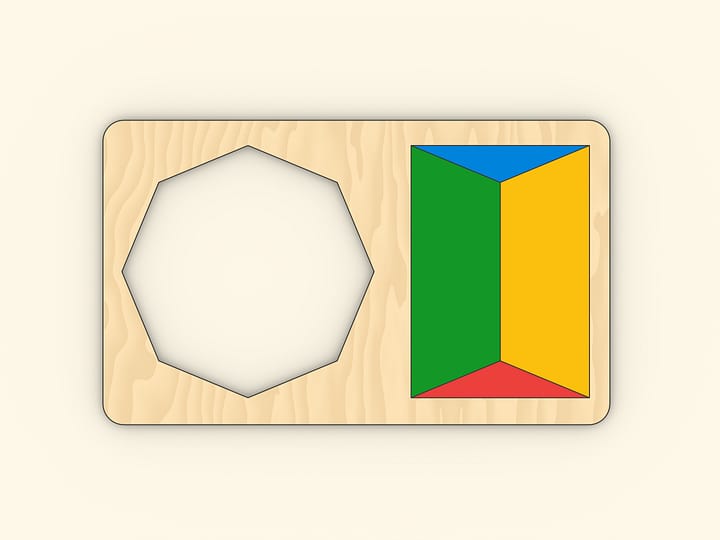
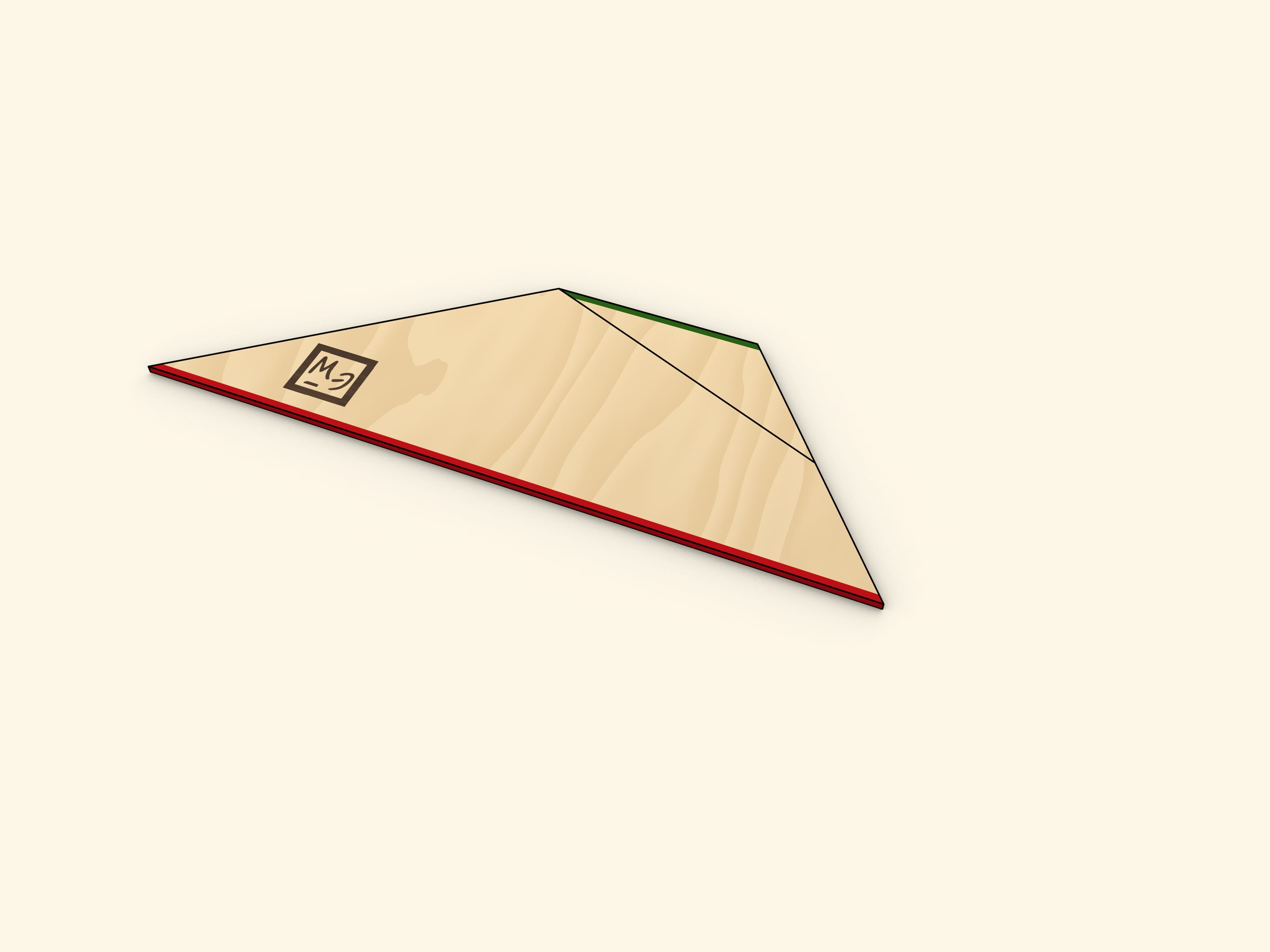
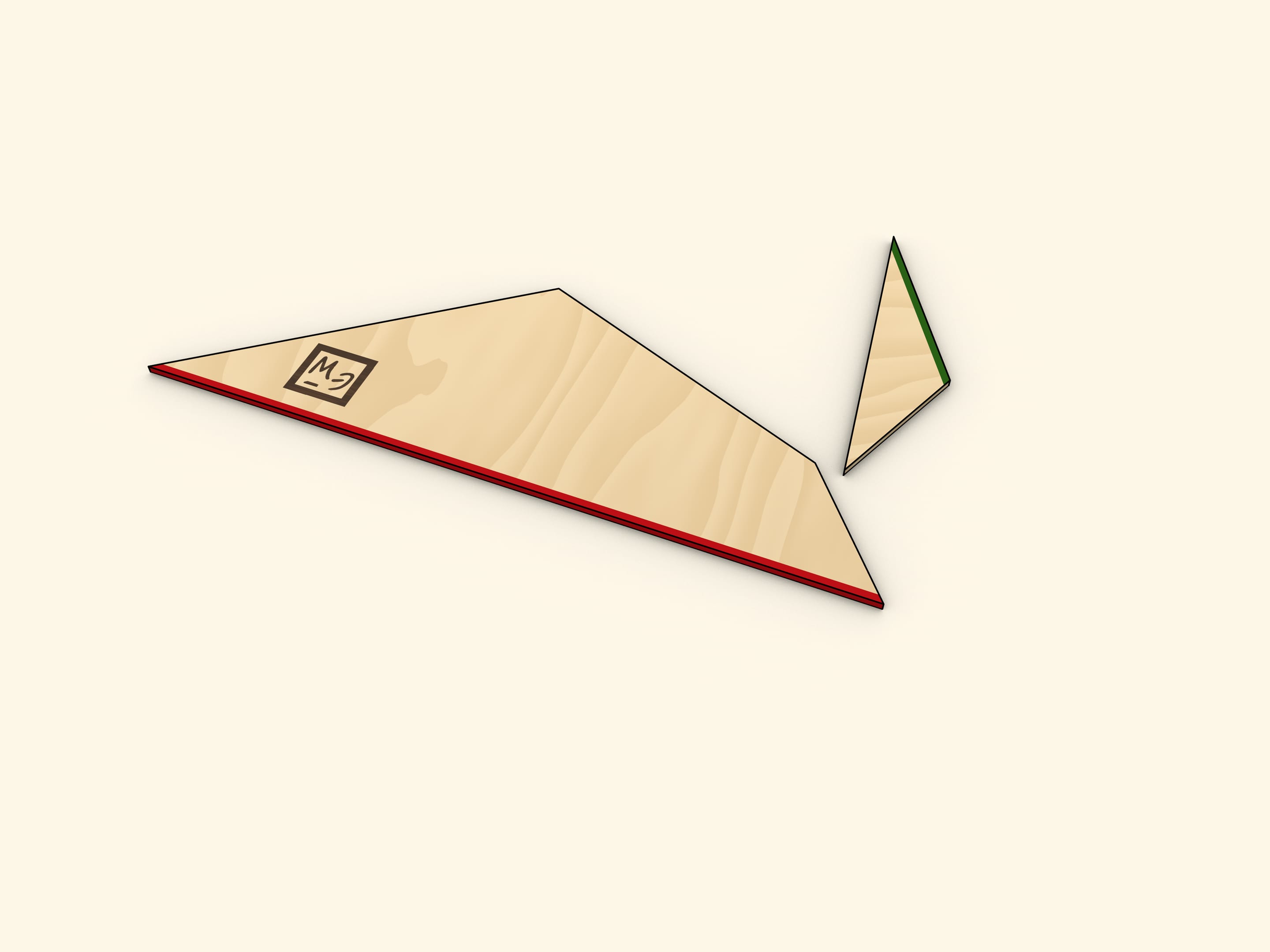
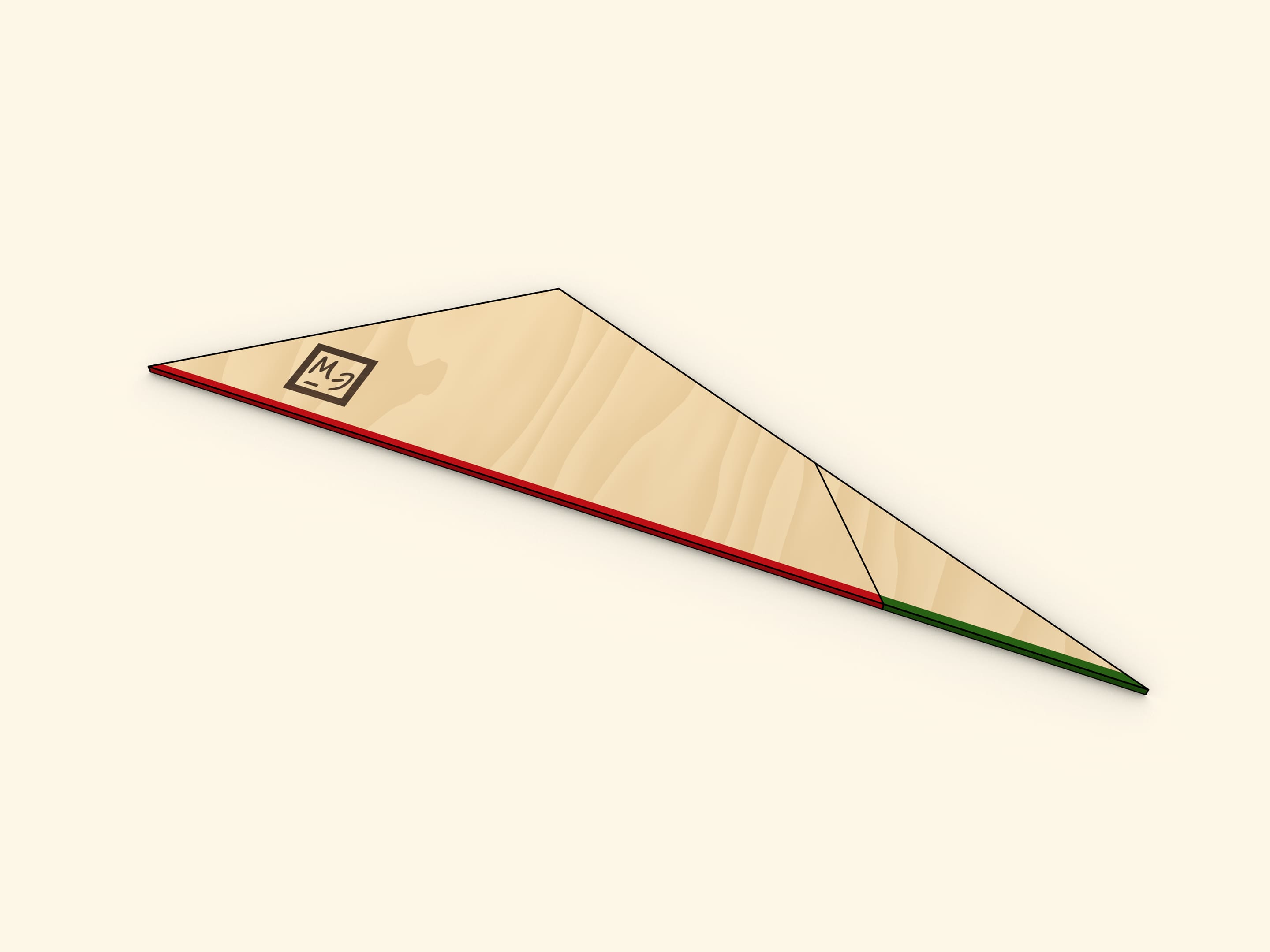
Свести трапецию к треугольнику можно разрезав её вдоль линии, соединяющей вершину с серединой противоположной боковой стороны. Повернём отрезанный треугольник до того момента, когда оба основания трапеции окажутся на одной прямой. Убедитесь, что две части боковой стороны при этом лягут на одну прямую, то есть, получится действительно треугольник.
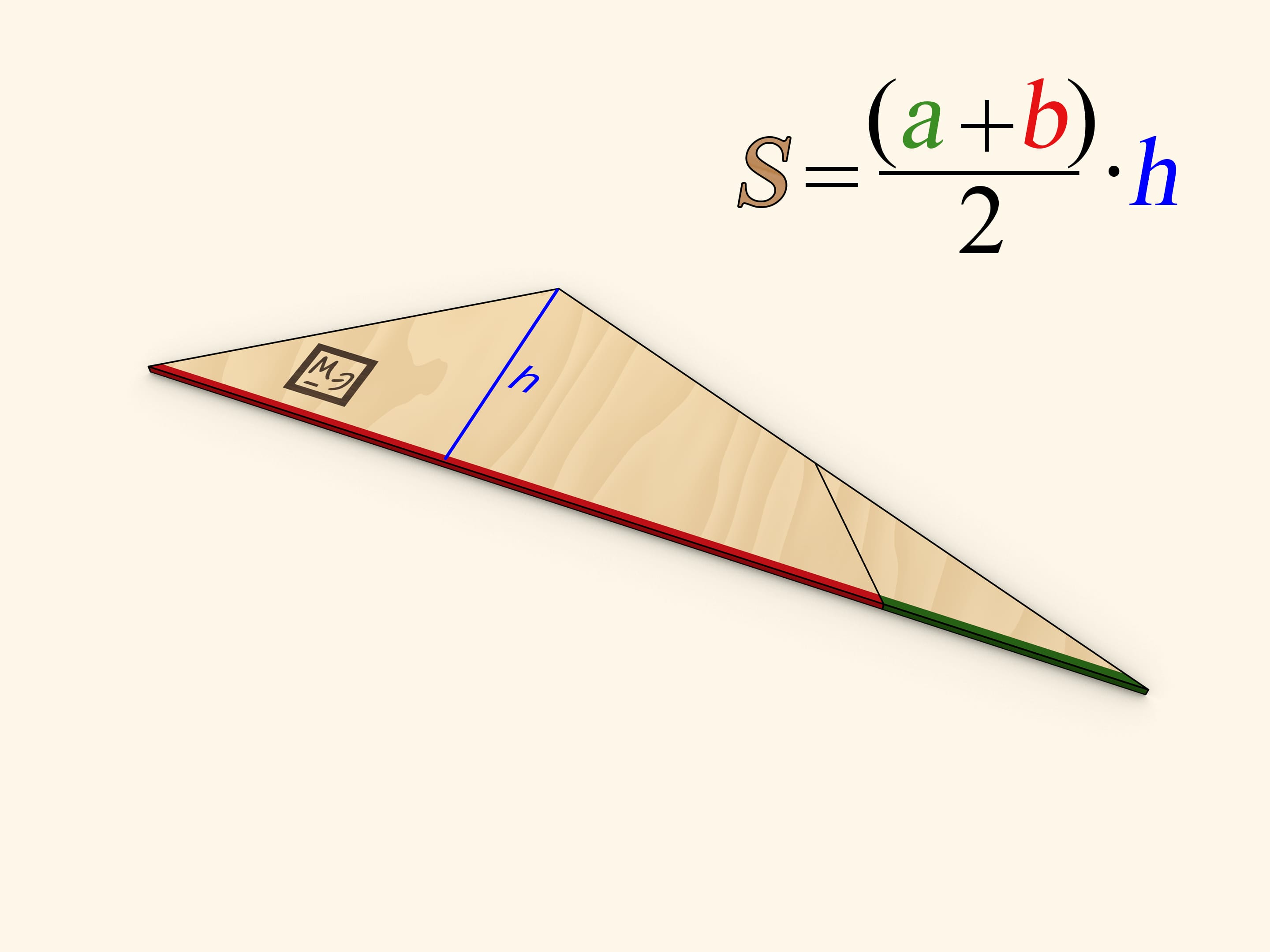
Одна из сторон получившегося треугольника имеет длину, равную сумме длин оснований трапеции, а длина высоты треугольника, проведённой к этой стороне, совпадает с высотой трапеции.
Один из способов подсчёта площади треугольника состоит в нахождении половины произведения длины стороны на длину высоты, опущенную на эту сторону. Применение этого способа и даёт привычную формулу площади трапеции.
Обе модели можно сделать из доски толщиной около 10 мм. Для удобства демонстрации части, на которые она разрезается, удобно соединять между собой при помощи магнитов.