“The Educated Monkey” can not only count in a row (as it did in Mikhail Zoshchenko’s short story with the same title), but can multiply and add numbers! If you move the monkey’s “legs” to the given numbers, its “hands” fingers will point at the result of the chosen operation.
The middle buttons switch the viewing mode between a historical model, its kinematic scheme or a combined view.
at the number desired
at the number desired
The history of creating an “Educated monkey” is related to a trained monkey, named Consul, visit to United States in the early 20th century. It was able to imitate many human actions, including operating the cash register. It participated in many popular shows in different parts of the USA. In 1909 even a short film titled “Consul crosses the Atlantic” was released — at that time, the planes couldn’t fly long distances, one could get to America by ship only, spending more than a week in a voyage across the Atlantic ocean.
In 1910, the monkey performed in city of Dayton, where the NCR company, which produced cash registers and held a large collection of such devices, was situated. (Now this company is known for its ATMs, which are also used in Russia).
In 1915, NCR’s draftsman William Henry Robertson, who previously worked as a mathematics teacher in secondary school and had heard stories about Consul visits to the company, applied for two patents. The first patent covered “calculating device” for a “quick and simple method of searching results” on the diagram. Such a method for solving equations is called nomography. The second patent covered a toy, based on the same mechanism, “for stimulating children’s interest in learning numbers”. The mentioned toy was implemented as a monkey. Finally, in 1916 the toy “Consul: The Educated Monkey” appeared in catalogues.
“The Educated Monkey” can multiply and square numbers from 1 to 12. The reason is that States had inherited “school” multiplication table from Britain. In English system of length measures 1 foot is equal to 12 inches; until 1971 the monetary unit of 1 shilling was equal to 12 pence, and in weight system of measures, used by The Royal Mint to this day, 1 pound equals 12 ounces. The multiplication table, being an education system instrument, is “adapted” to the country and in the US, it is traditionally 12×12. In Russia metrical (decimal) measure system was implemented as a non-mandatory system at the end of 19th century, and as a mandatory — in 1917—1925. Thus, Russians are used to a 10×10 multiplication table.
“The Educated Monkey” is a planar hinge mechanism.
The construction of the device is symmetrical, the basis of the mechanism is two equal isosceles right-angled triangles. Each hypotenuse at one end is resting on a number line, where these support points ($L$ and $R$) can slide. Another ends of triangles’ hypotenuses are hinged. (Such a construction can be imagined as two halves of a square cut along a vertical diagonal, the lower points of which can be slid apart).
Two additional links, hinged to each other in a point O, are also hinged to triangles at the vertex of the right angles. These links are equal in length to triangles’ catheti and together with them form a hinged rhombus.
The point $O$ is always in the middle between points $L$ and R: just like the hinge connecting the triangles, it lies on perpendicular bisector of segment LR. The choice of isosceles right-angled triangles ensures linear (with a coefficient of $1/2$) dependence of the point $O$ height above the number line on the segment $LR$ length — distance from the point $O$ to the line is always half the length of the segment $LR$ (a strict proof is given below).
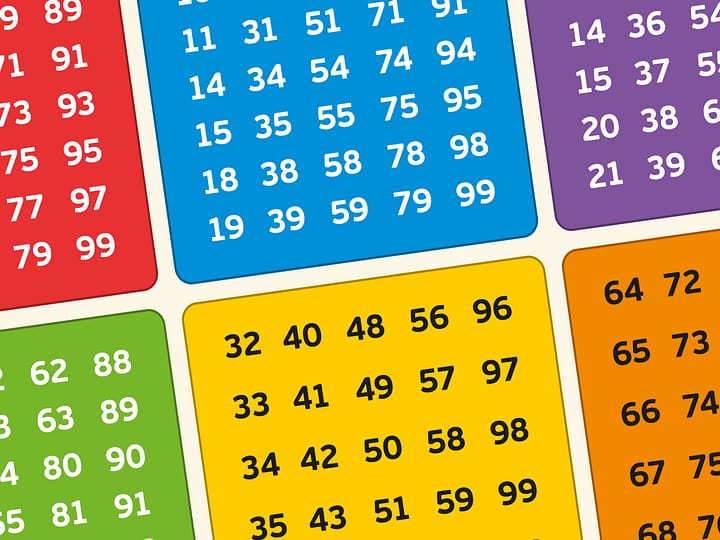
Since integers on the number line are uniformly distributed, then at all possible positions of $L$ and $R$ corresponding to the integers, the point $O$ positions will form a triangle of values, whose rows will be evenly spaced vertically and the positions inside one row will be in the middle between the positions in adjacent rows.
For example, if the points $L$ and $R$ are placed on the two adjacent integers, the point $O$ is located between them, at a distance of $1/2$ from the number line. If the points $L$ and $R$ are placed at a distance of two integers, then the point $O$ is located at a distance 1 from the number line in the middle between the positions in the previous row.
Thus, the “Educated Monkey” implements a binary operation: each position of “variables” $L$ and $R$ defines the unique position of the window, where the result of this operation can be written. If the order of the numbers on which points $L$ and $R$ are placed is not considered, the operation will be commutative i.e. it won’t depend on order of the numbers. For example, it’s possible to implement functions of multiplication and addition. If we additionally agree that when subtracting, the smaller number is always subtracted from the bigger one, and when dividing, the bigger number is always divided by the smaller, then it’s possible to implement non-commutative functions of subtraction and division.
To apply the chosen operation to two identical numbers, for example, to get a square when multiplying, a special extra “square” position is added for the point $R$ to the right of the number line. The triangle of values is expanded with corresponding numbers — squares of integers where the $L$ point is placed.
For each chosen operation a specific triangle of values is composed and placed on the field.
For a complete description of the classic model of “The Educated Monkey” it’s worth noting that the rectangular window, which is pointed at by the monkey’s fingers, is placed above the point $O$. To ensure that the window is always in upright position, it’s made as a part of “tail” link, which slides its slot on the hinge connecting the triangles, located in a butterfly. The same link also holds the head in an upright position.
The “tail” link isn’t needed to make a simplified model without the head and with round window right at the $O$ point. This simplification also makes it so the “tail” does not protrude beyond the field even at distant positions of the $L$ and $R$ points.
Let’s prove that the choice of main blue triangles as isosceles right-angled in the construction of the monkey ensures linear (with a coefficient of $1/2$) dependence of the point height above the number line on the segment length. It is required so the rows of values triangle are evenly spaced vertically.
To find the height of the $O$ point let us circumscribe a rectangle with horizontal and vertical sides around one of the isosceles right-angled triangles. One vertical side of a rectangular lies on symmetry axis of the construction, while the other goes through the vertex of the blue triangle’s right angle. The resulted red-colored triangles are equal (they are right-angled, their catheti are equal and their angles are also equal). Let’s draw a horizontal diagonal of a green hinged rhombus, a horizontal segment through the point $O$ and a vertical segment through the point $R$. Three red segments are equal. Since the horizontal diagonal of rhombus divides the vertical diagonal in half, the pink segment has the same length. Thus, the violet segments are also equal. Therefore, the violet quadrilateral is always — in every position of the $L$ and $R$ points — a square. One of its sides is equal to the height of the $O$ point above a number line, and the other, because of symmetry, is half the segment LR.
If we omit the isoscelessness of blue triangles or the presence of right angle in it, the rows in the values triangle won’t be evenly spaced vertically. However, in case of self-made model, abandonment of these criteria simplifies the construction of monkey’s legs, while nonlinearity will hardly be noticeable.
The mathematical theory of planar hinge mechanisms — lines of different length, hinged at the ends — is still develops today. In 2005, for example, “The Signatures Theorem” was proved: for any signature there is a planar hinge mechanism that can precisely reproduce that signature. But the theorem is not yet constructive — it is proved that for every signature such a mechanism exists, but mathematicians do not yet know how to build one for a particular signature.