Пятый постулат Евклида равносилен утверждению, что через точку, не лежащую на прямой, можно провести ровно одну прямую, параллельную данной. Если пятый постулат не выполняется, то возможны две ситуации. Через точку, не лежащую на прямой, нельзя провести ни одной прямой, параллельной данной. Получается сферическая геометрия. Через точку, не лежащую на прямой, можно провести бесконечно много прямых, параллельных данной. Получается геометрия Лобачевского. Чем различаются эти геометрии и в чём их сходства — наглядно представлено на плакатах.
Представленные плакаты можно скачать и распечатать на бумаге формата «А». Минимальный размер — листы А3.
Три геометрии: сходства и различия
Евклидова
геометрия
геометрия
Сферическая
геометрия
геометрия
Геометрия
Лобачевского
Лобачевского
Евклид (Εὐκλείδης; Александрия, III век до н. э.).
«Начала» (др.-греч. Στοιχεῖα, лат. Elementa), определения:
точка есть то, что не имеет частей;
линия — длина без ширины;
прямая линия есть та, которая равно лежит на всех своих точках;
···
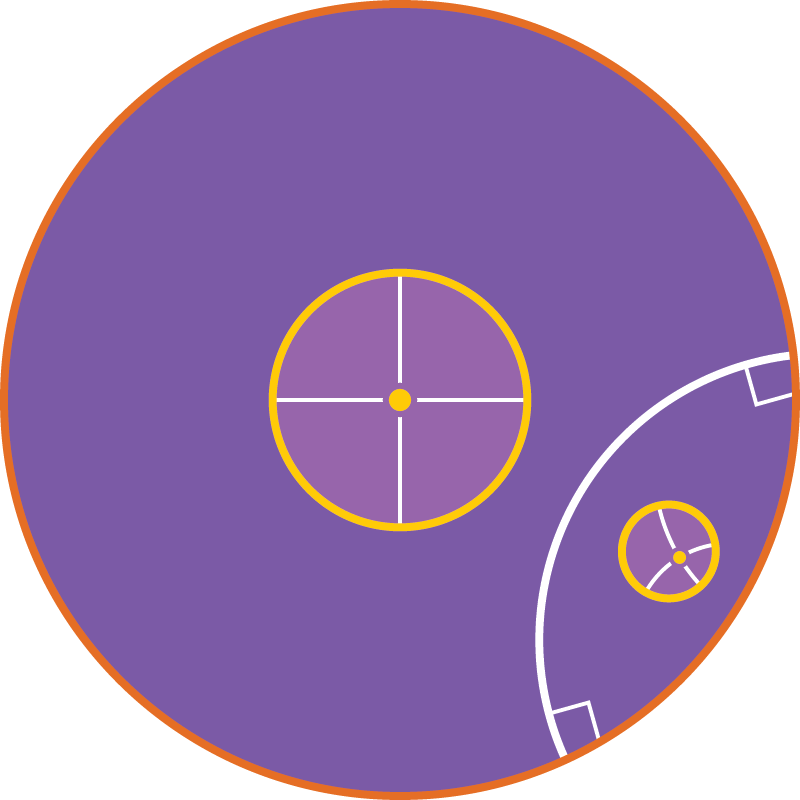
Точки — точки на единичной сфере, прямые — большие круги (сечения сферы плоскостями, проходящими через центр).
Расстояния — обычные длины (по сфере) отрезков прямых.
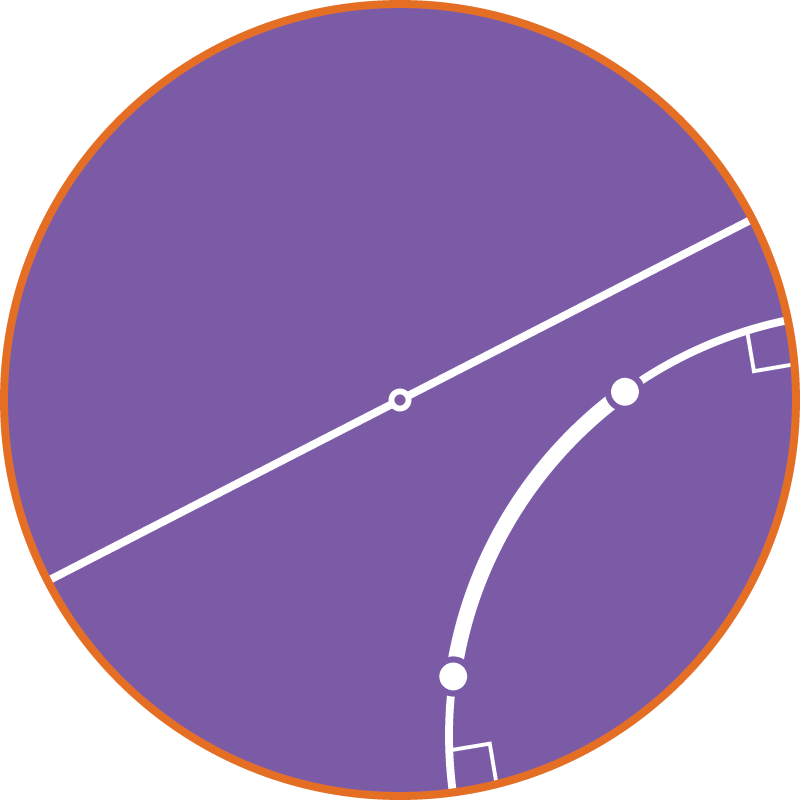
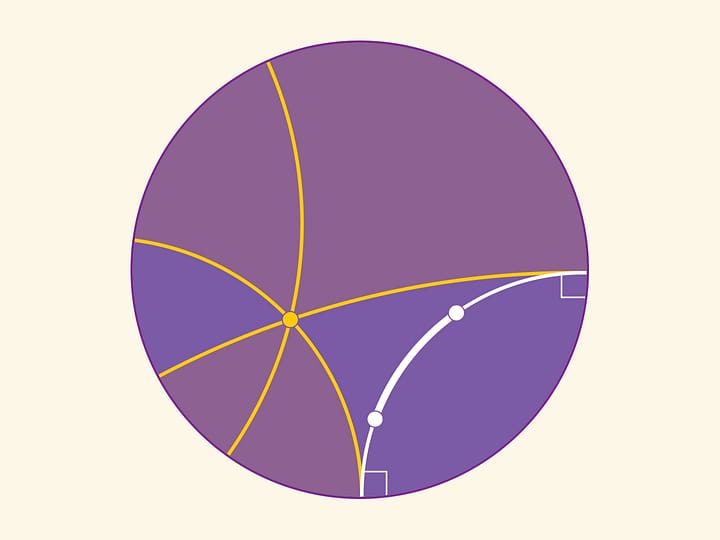
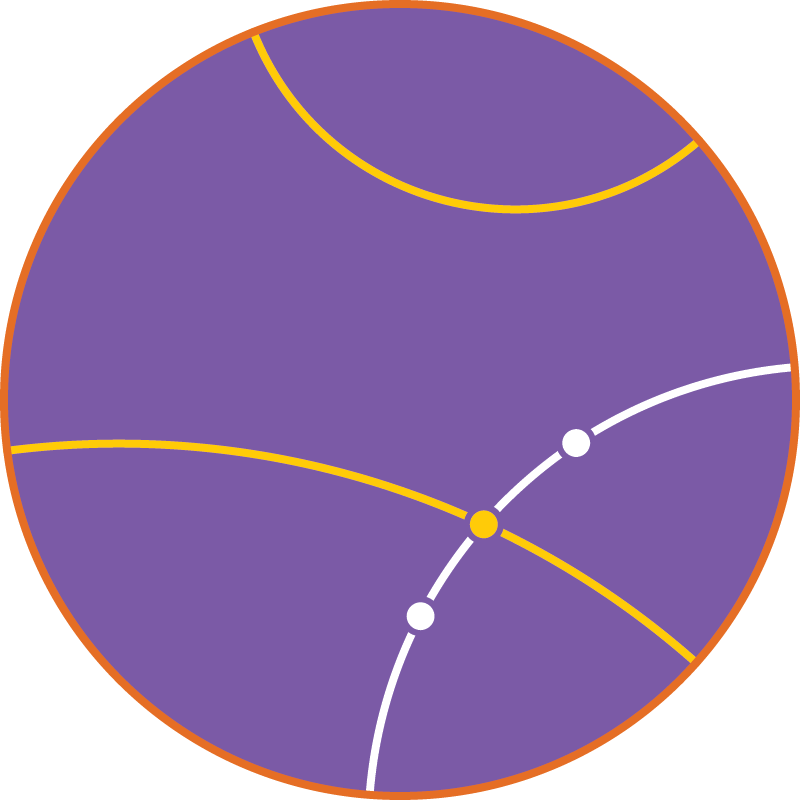
Модель Пуанкаре в круге:
точки — точки внутри окружности («абсолюта»),
прямые — дуги обычных окружностей, перпендикулярные абсолюту, и диаметры абсолюта.
Расстояния не совпадают с длинами дуг в обычном смысле.
Через точку, не лежащую на прямой, можно провести ровно одну прямую, параллельную данной.
Пятый постулат Евклида.
Через точку, не лежащую на прямой, нельзя провести ни одной прямой, параллельной данной.
Параллельными называются прямые, не имеющие общих точек.
Через точку, не лежащую на прямой, можно провести бесконечно много прямых, параллельных данной.
Параллельными называются прямые, не имеющие общих точек.
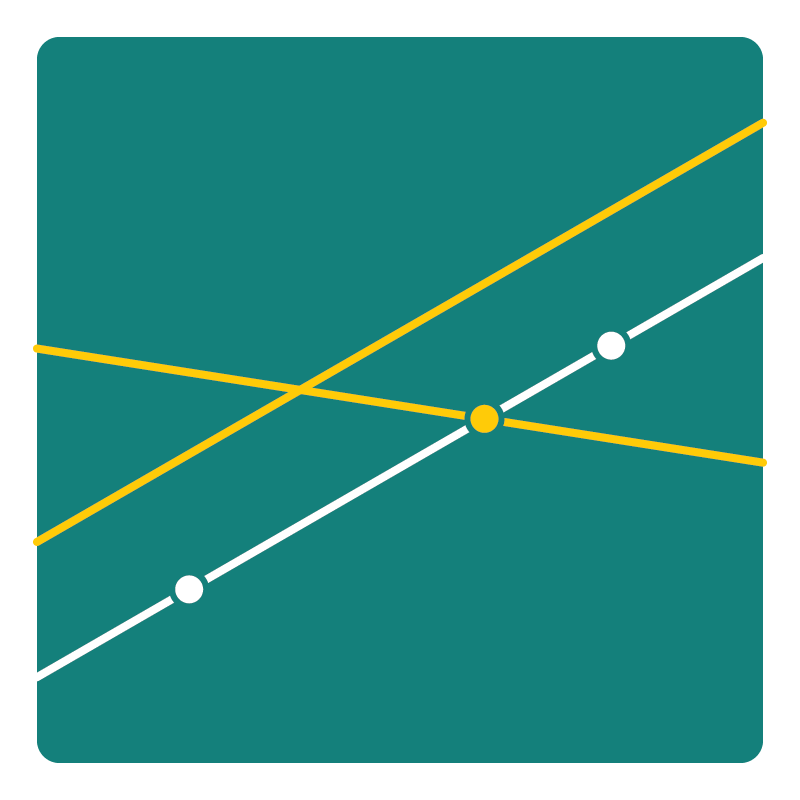
Через две различные точки можно провести ровно одну прямую; две различные прямые имеют не более одной общей точки.
Через две близкие точки можно провести ровно одну прямую; две различные прямые имеют ровно две общие точки.
Через диаметрально противоположные точки можно провести бесконечно много прямых.
Через две различные точки можно провести ровно одну прямую; две различные прямые имеют не более одной общей точки.
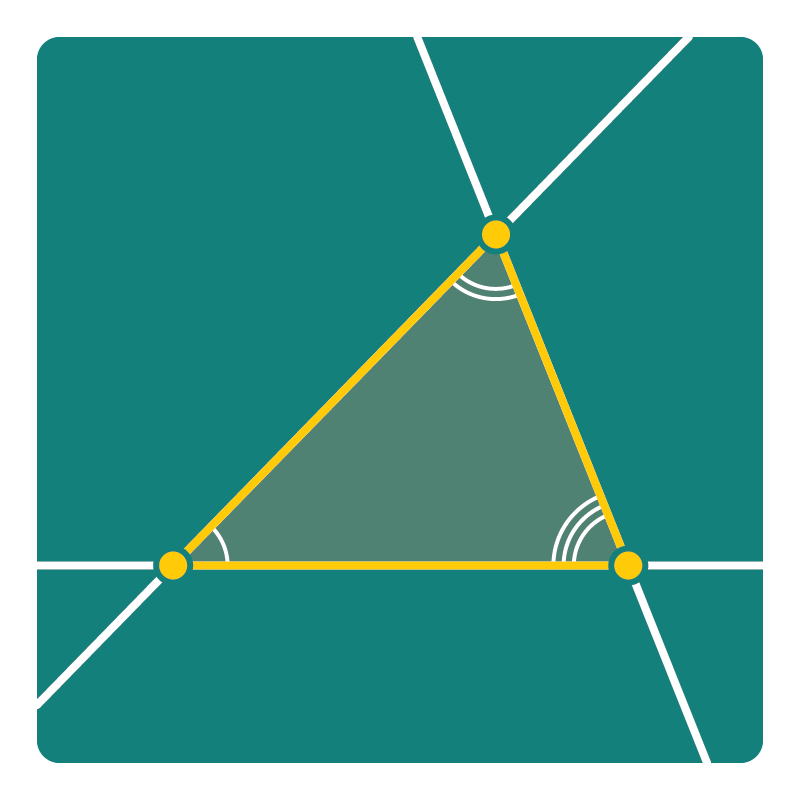
Сумма углов треугольника равна $\pi$.
Сумма углов треугольника больше $\pi$.
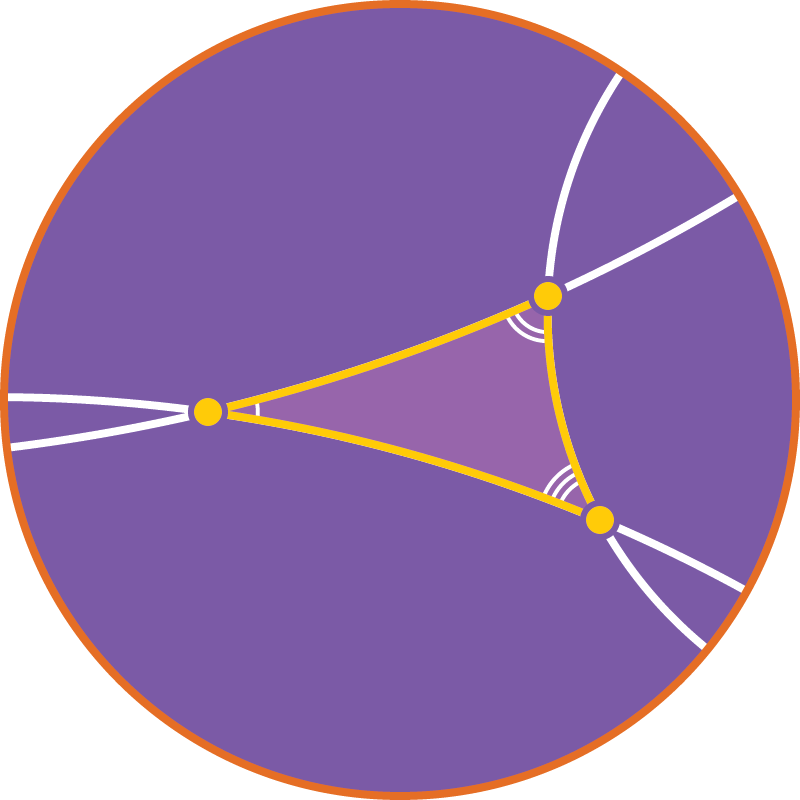
Сумма углов треугольника меньше $\pi$.
Площадь треугольника не выражается через только его углы.
Площадь треугольника с углами $\alpha$, $\beta$, $\gamma$ равна $(\alpha+\beta+\gamma)-\pi$.
Площадь треугольника с углами $\alpha$, $\beta$, $\gamma$ равна $\pi-(\alpha+\beta+\gamma)$.
Существуют подобные, но не равные, многоугольники.
Стороны треугольника не определяются его углами.
Подобных, но не равных, многоугольников не существует.
Стороны треугольника выражаются через его углы.
Подобных, но не равных, многоугольников не существует.
Стороны треугольника выражаются через его углы.
Для прямоугольных треугольников $c^2=a^2+b^2$.
Теорема Пифагора.
Для прямоугольных треугольников $\cos c=\cos a\cos b$. Как следствие, $c^2 \lt a^2+b^2$.
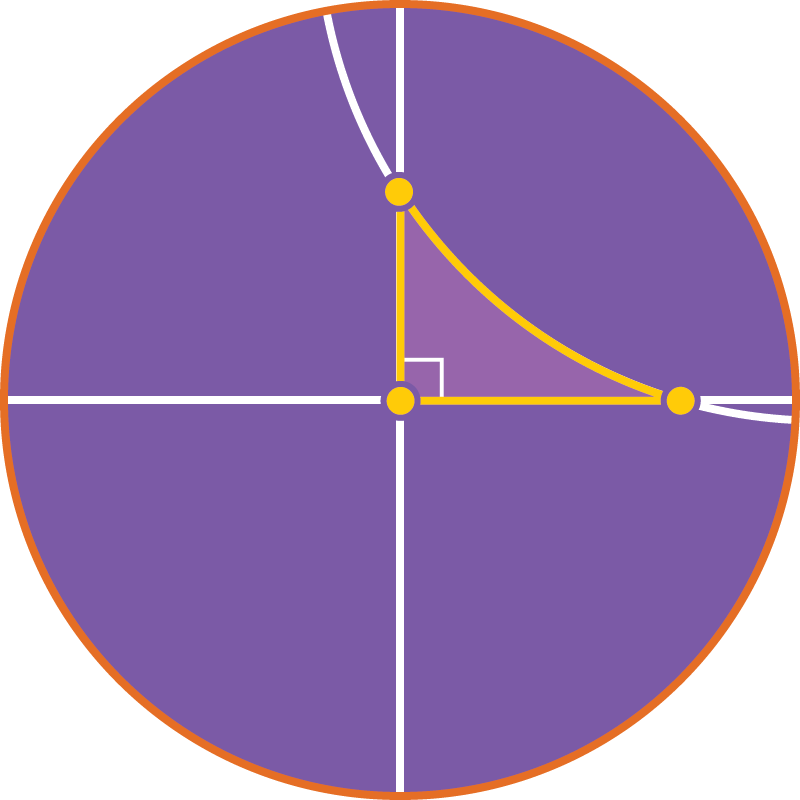
Для прямоугольных треугольников $\ch c=\ch a\ch b$. Как следствие, $c^2 \gt a^2+b^2$.
Длина окружности радиуса $r$ равна $2\pi r$.
Длина окружности радиуса радиуса $r$ равна $2\pi\sin r$.
Длина окружности ограничена (не больше длины прямой — большого круга).
Длина окружности радиуса радиуса $r$ равна $2\pi\sh r$.
Длина окружности очень быстро (экспоненциально) растёт с ростом $r$.
Множество точек, удаленных от данной прямой на данное расстояние, — пара прямых.
Множество точек, удаленных от данной прямой на данное расстояние, — пара окружностей (или точек).
Множество точек, удаленных от данной прямой на данное расстояние, — пара эквидистант (не прямых и не окружностей).
В модели Пуанкаре эквидистанты — дуги с концами на абсолюте, не перпендикулярные абсолюту (и хорды, не являющиеся диаметрами).
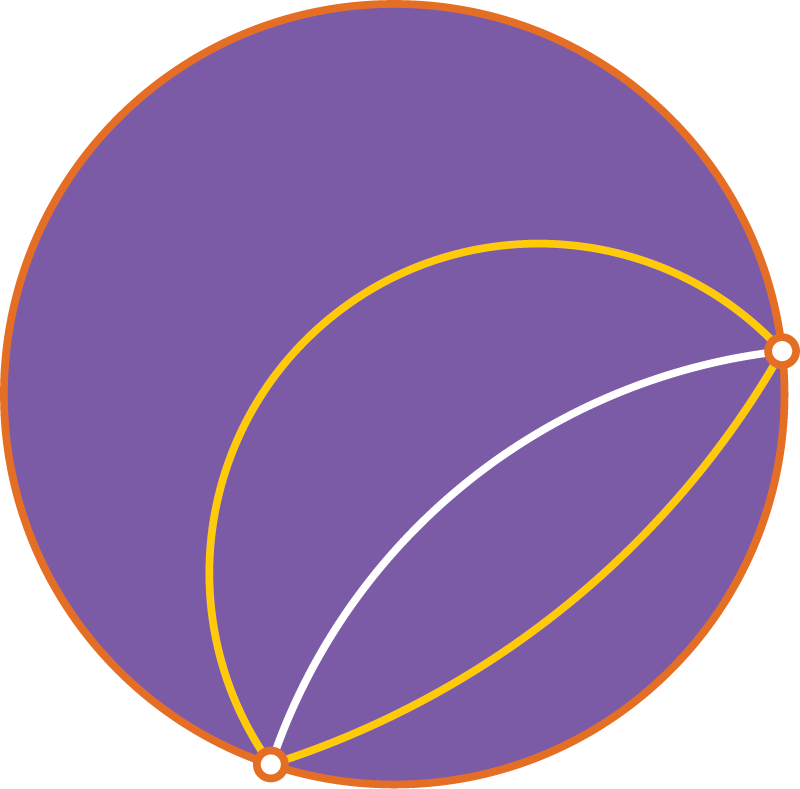
Любые три точки лежат либо на одной прямой,
либо на одной окружности.
Любые три точки лежат на одной окружности.
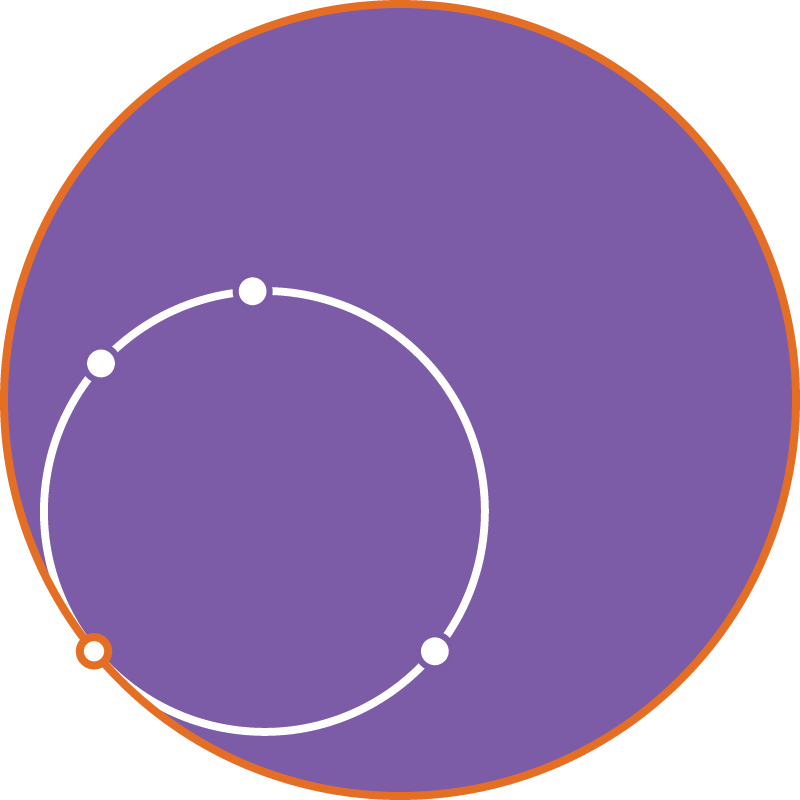
Любые три точки лежат либо на одой прямой,
либо на одной окружности,
либо на одной эквидистанте,
либо на одном орицикле.
В модели Пуанкаре орициклы — окружности, касающиеся абсолюта.
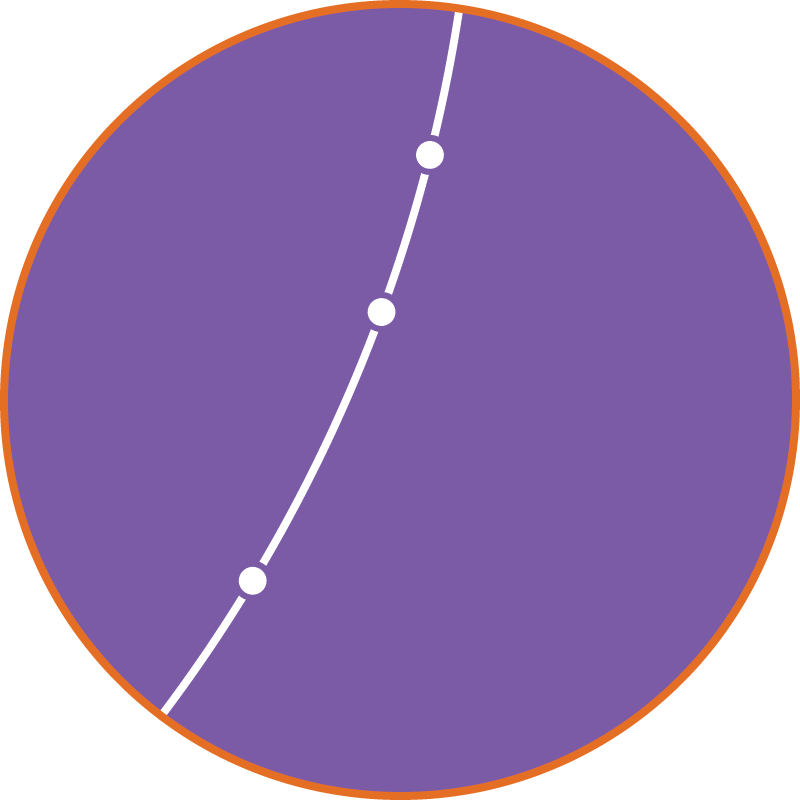
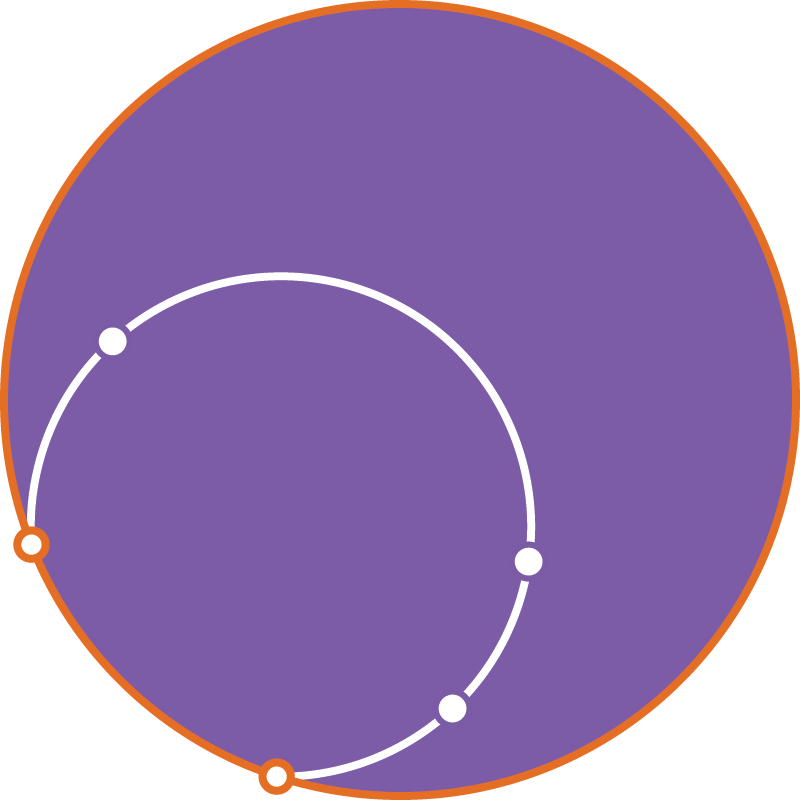
Сохраняющее ориентацию движение — либо поворот, либо параллельный перенос (сдвиг вдоль прямой).
Сохраняющее ориентацию движение — поворот.
Сохраняющее ориентацию движение — либо поворот, либо сдвиг вдоль прямой, либо сдвиг вдоль орицикла.
Существуют замощения одинаковыми правильными треугольниками, квадратами, шестиугольниками.
Существует замощение одинаковыми правильными $n$-угольниками, встречающимися по $k$ в каждой вершине, если $\frac1n+\frac1k=\frac12$.
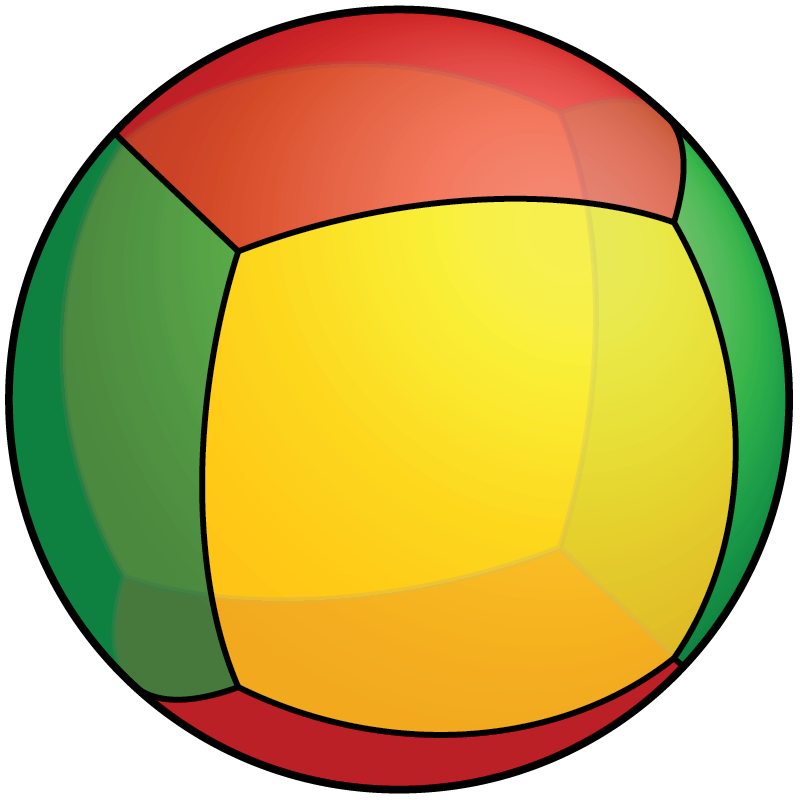
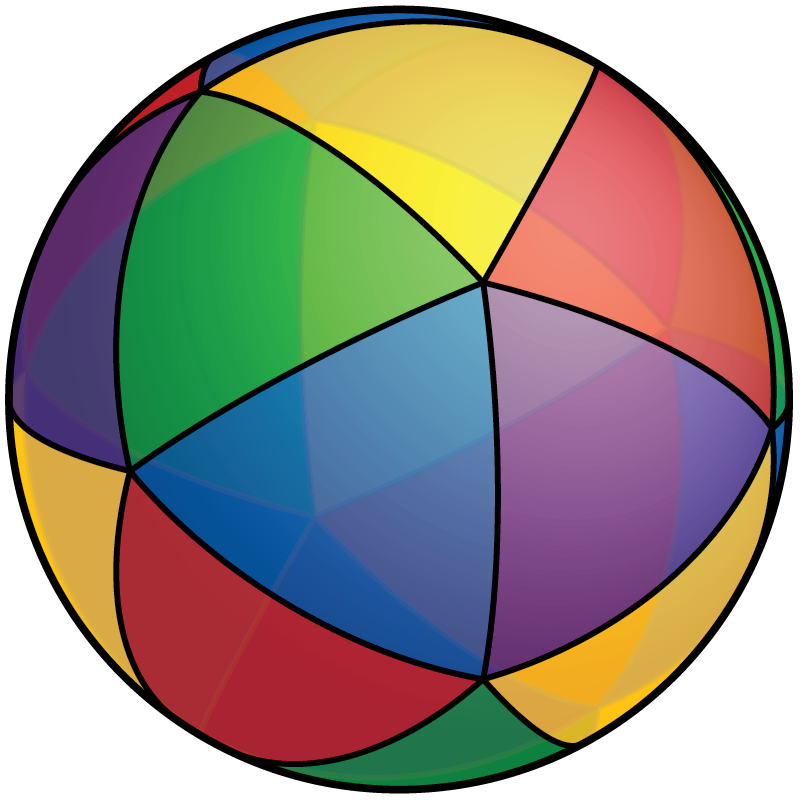
Существуют замощения одинаковыми правильными треугольниками, четырехугольниками, пятиугольниками.
Существует замощение одинаковыми правильными $n$-угольниками, встречающимися по $k$ в каждой вершине, если $\frac1n+\frac1k\gt\frac12$.
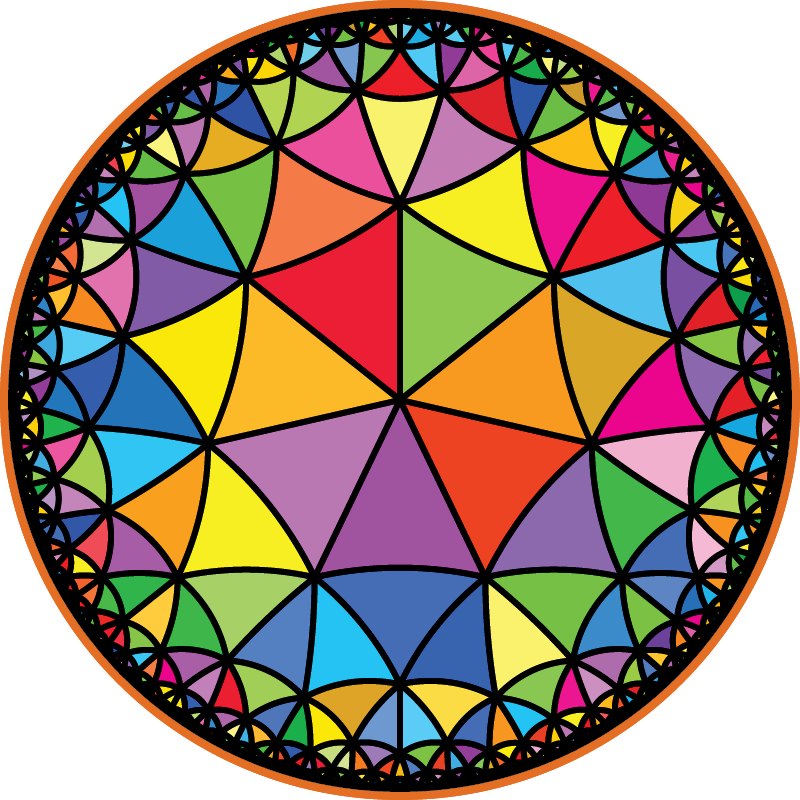
Существуют замощения одинаковыми правильными $n$-угольниками для любого $n$.
Существует замощение одинаковыми правильными $n$-угольниками, встречающимися по $k$ в каждой вершине, если $\frac1n+\frac1k\lt\frac12$.
Многие утверждения школьной планиметрии имеют аналоги и в сферической, и в неевклидовой геометриях. Но если в формулировке утверждения или в его доказательстве используется параллельность прямых, счёт углов, подобные треугольники, то возникают различия. Например, во всех трёх геометриях медианы треугольника пересекаются в одной точке. Но утверждение, что эта точка делит медианы в отношении $2 : 1$, вернo только в евклидовой геометрии.
