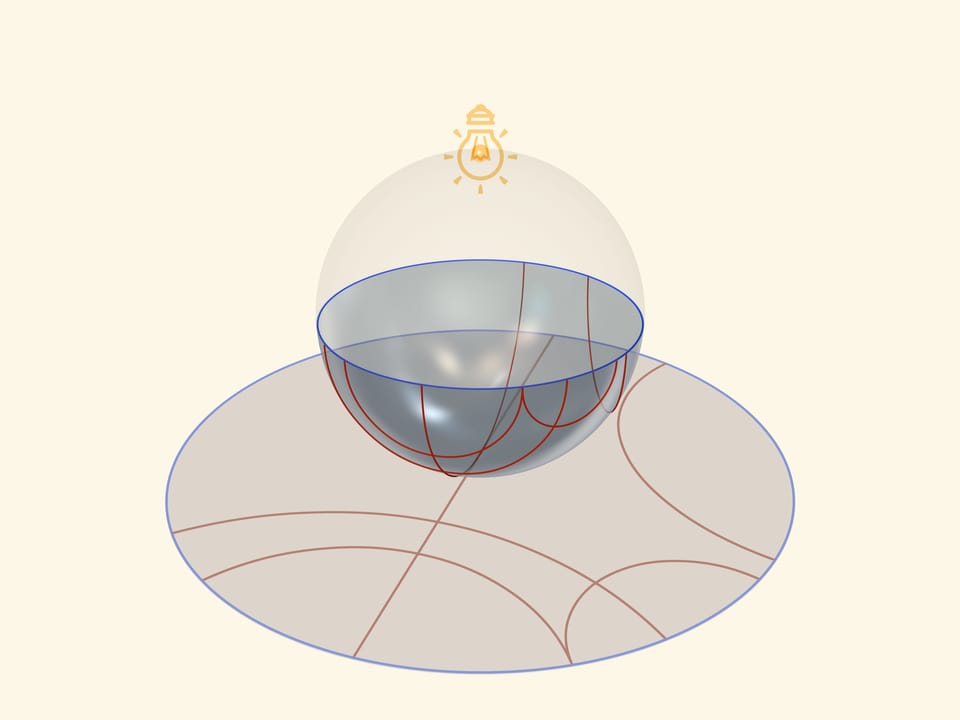
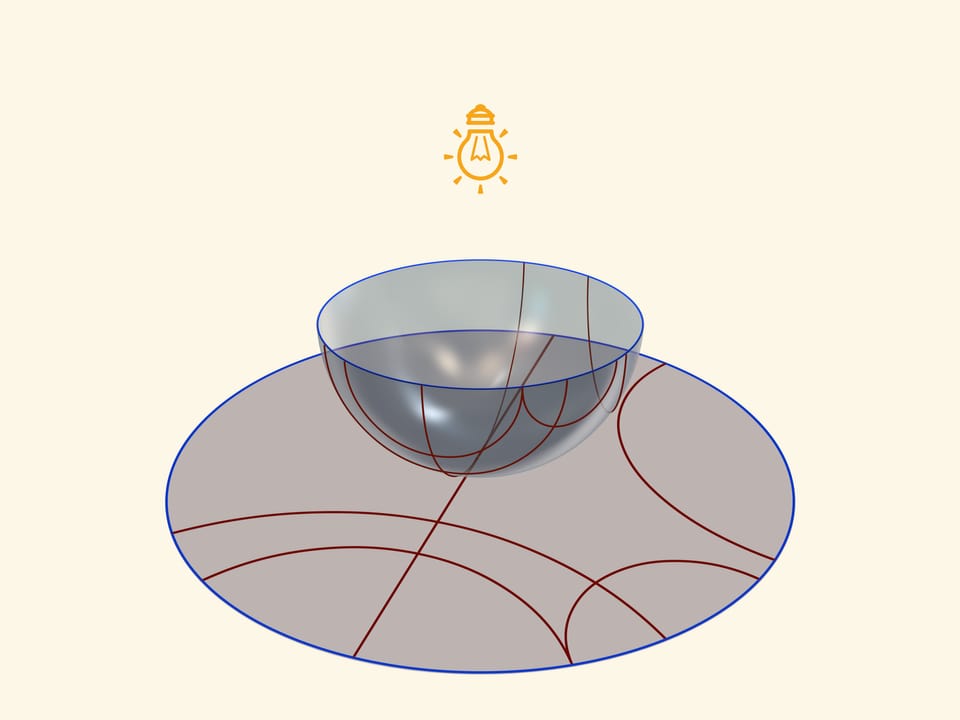
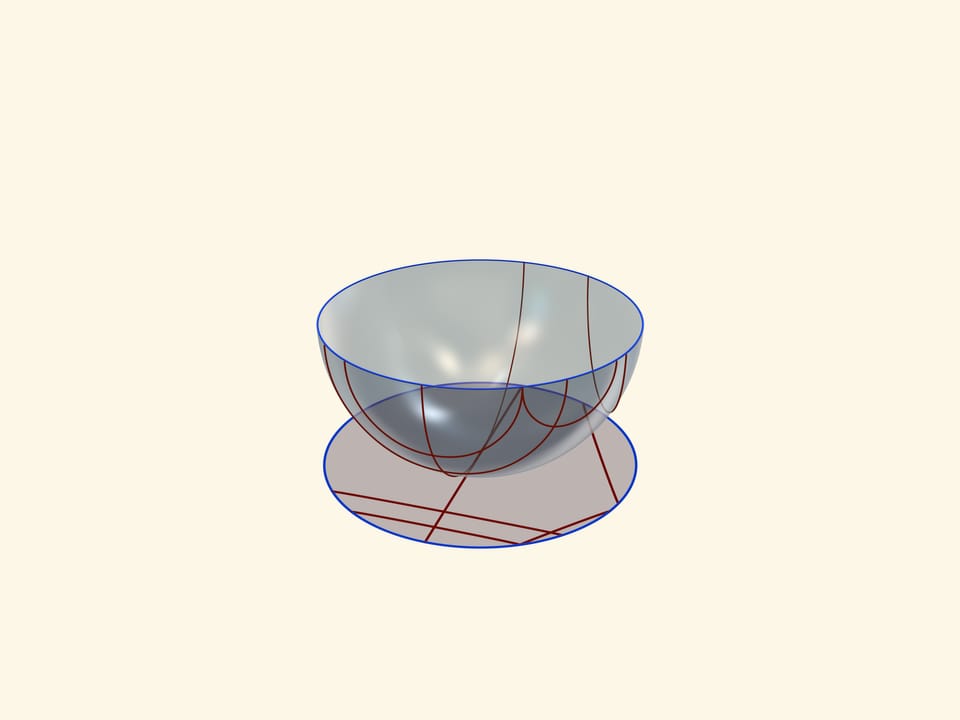
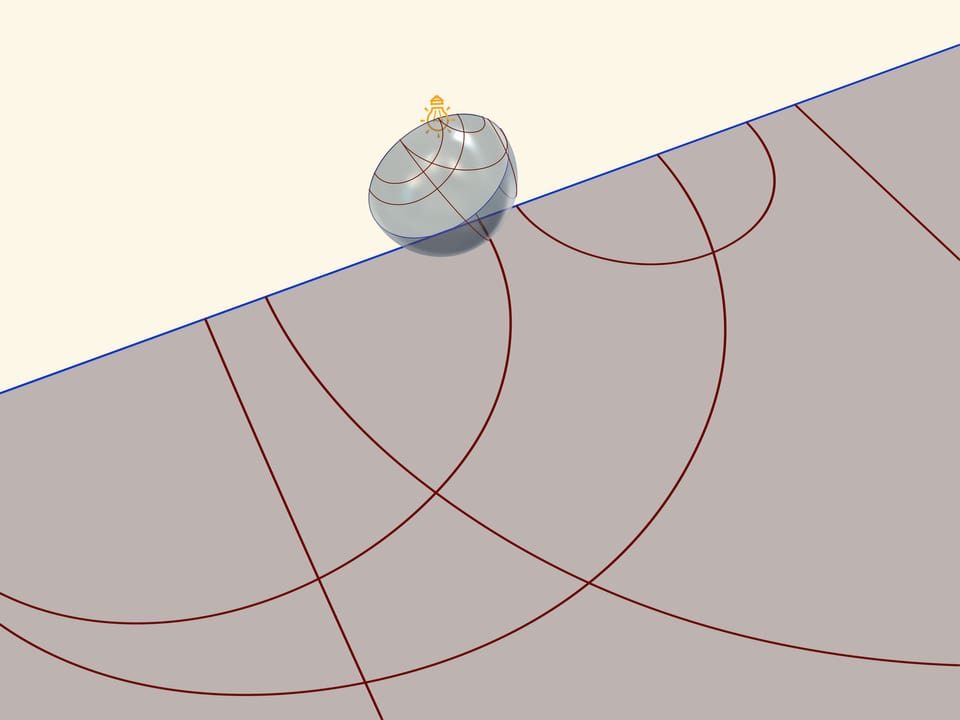
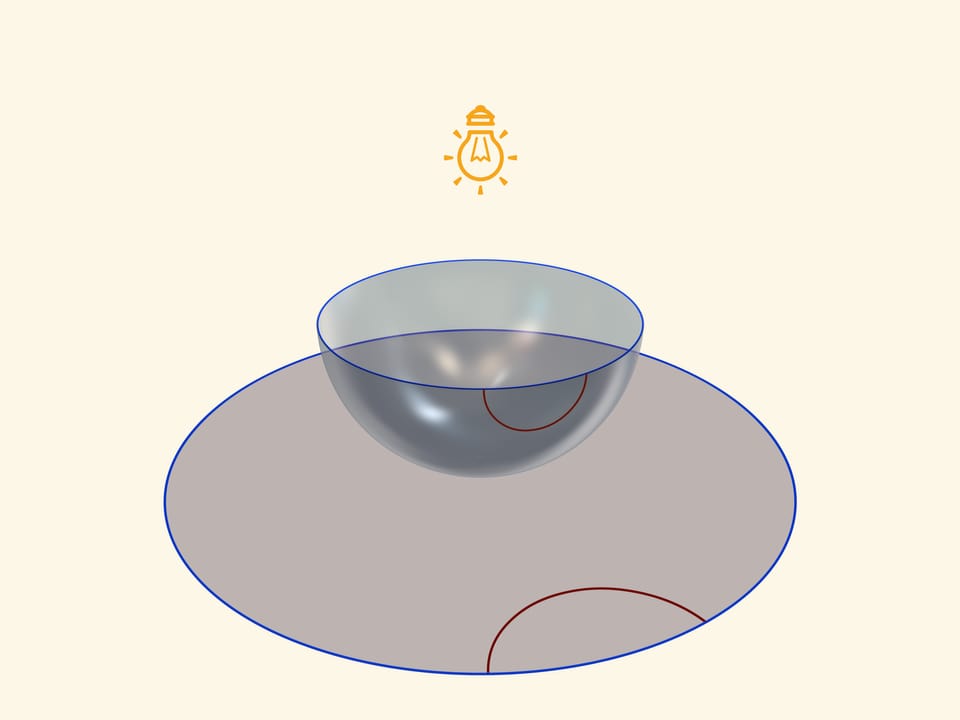
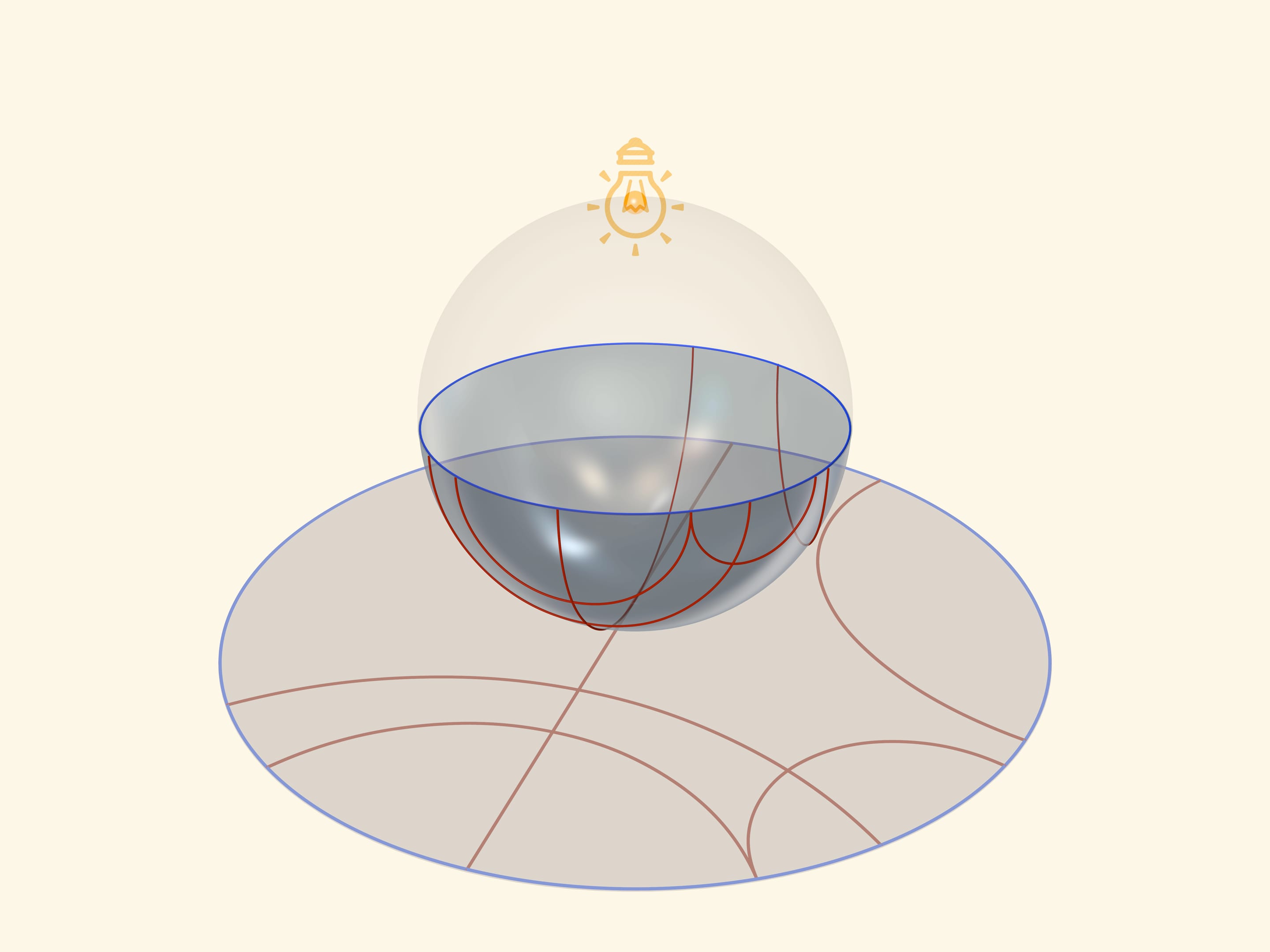
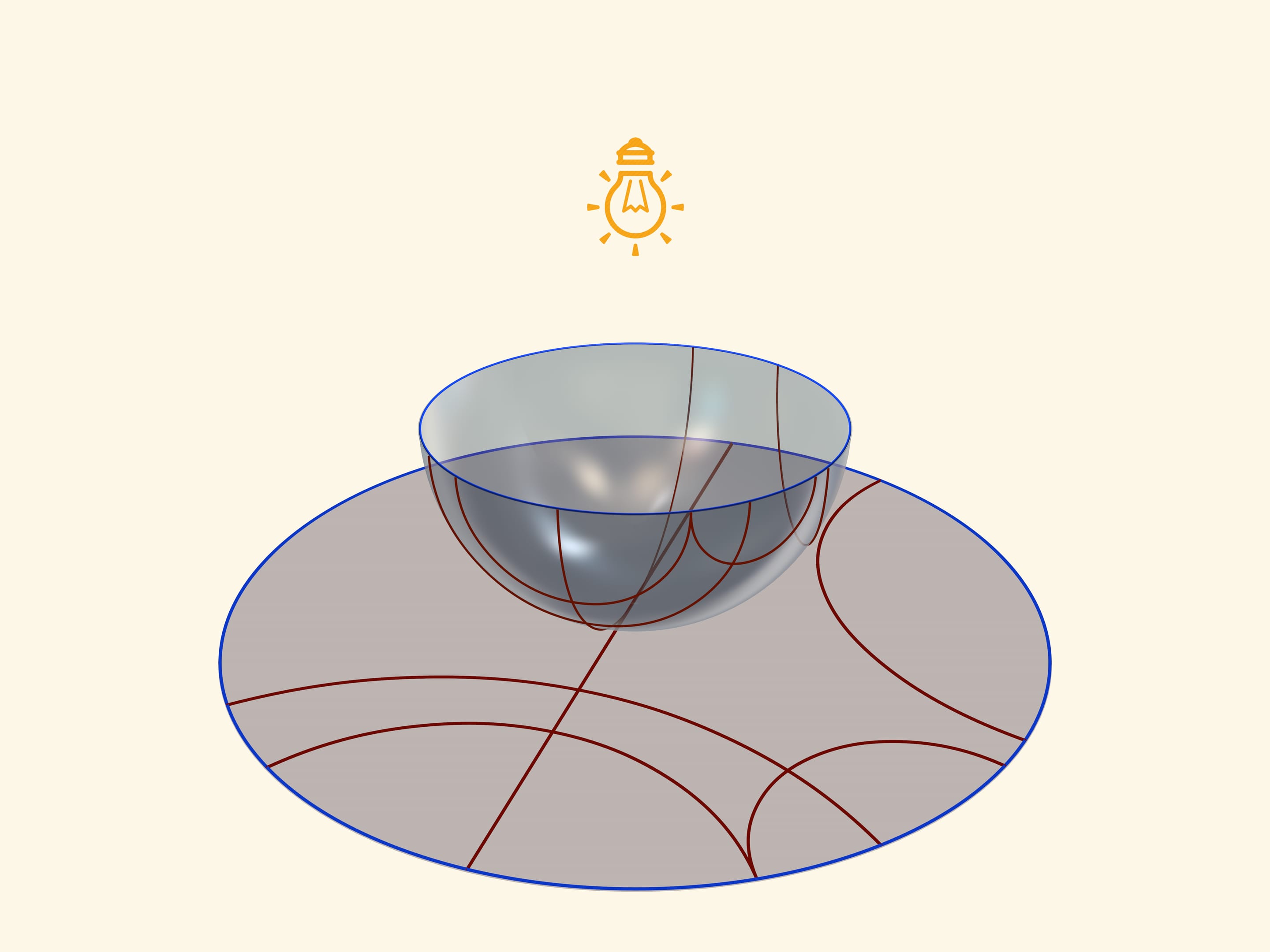
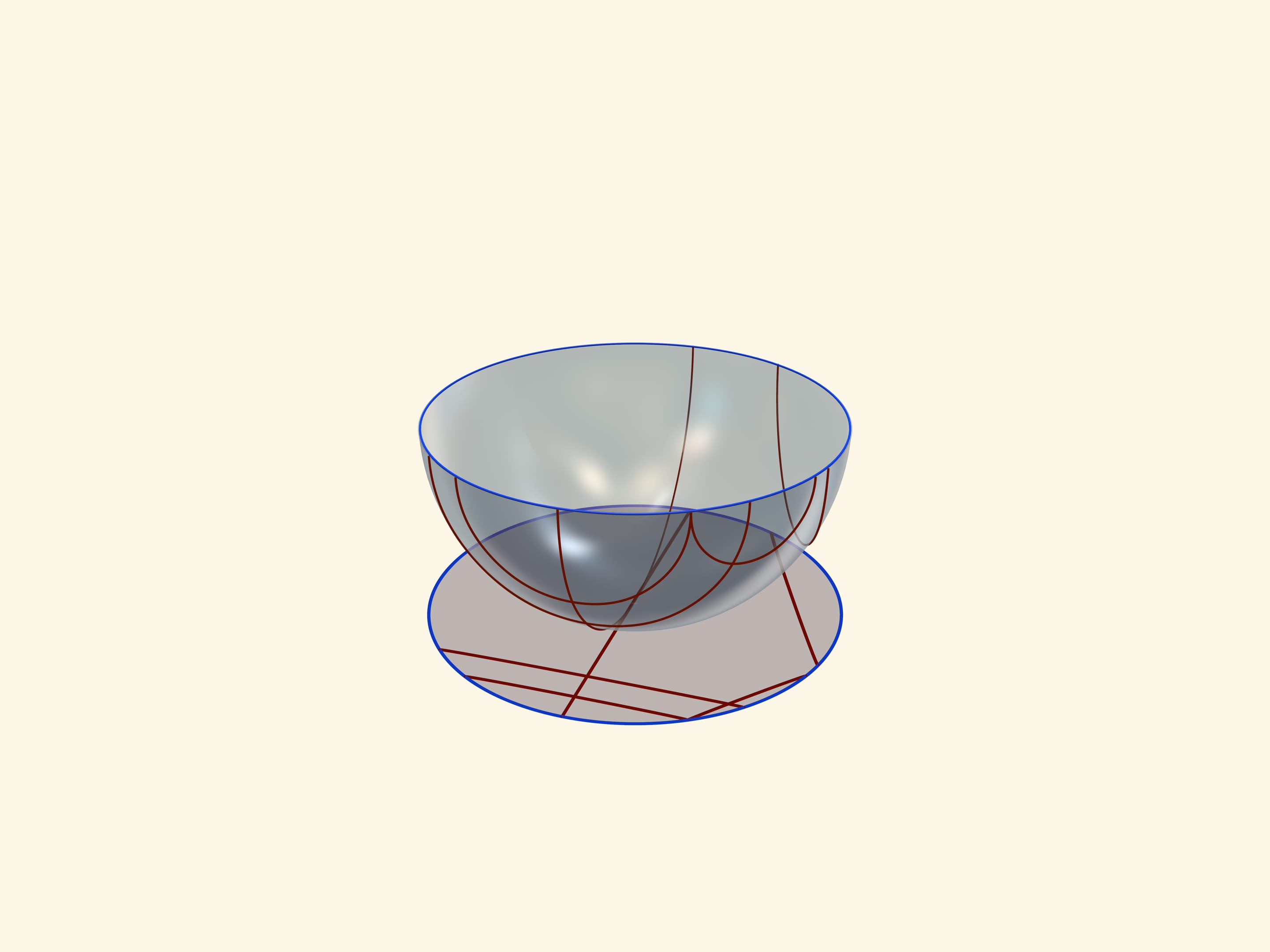
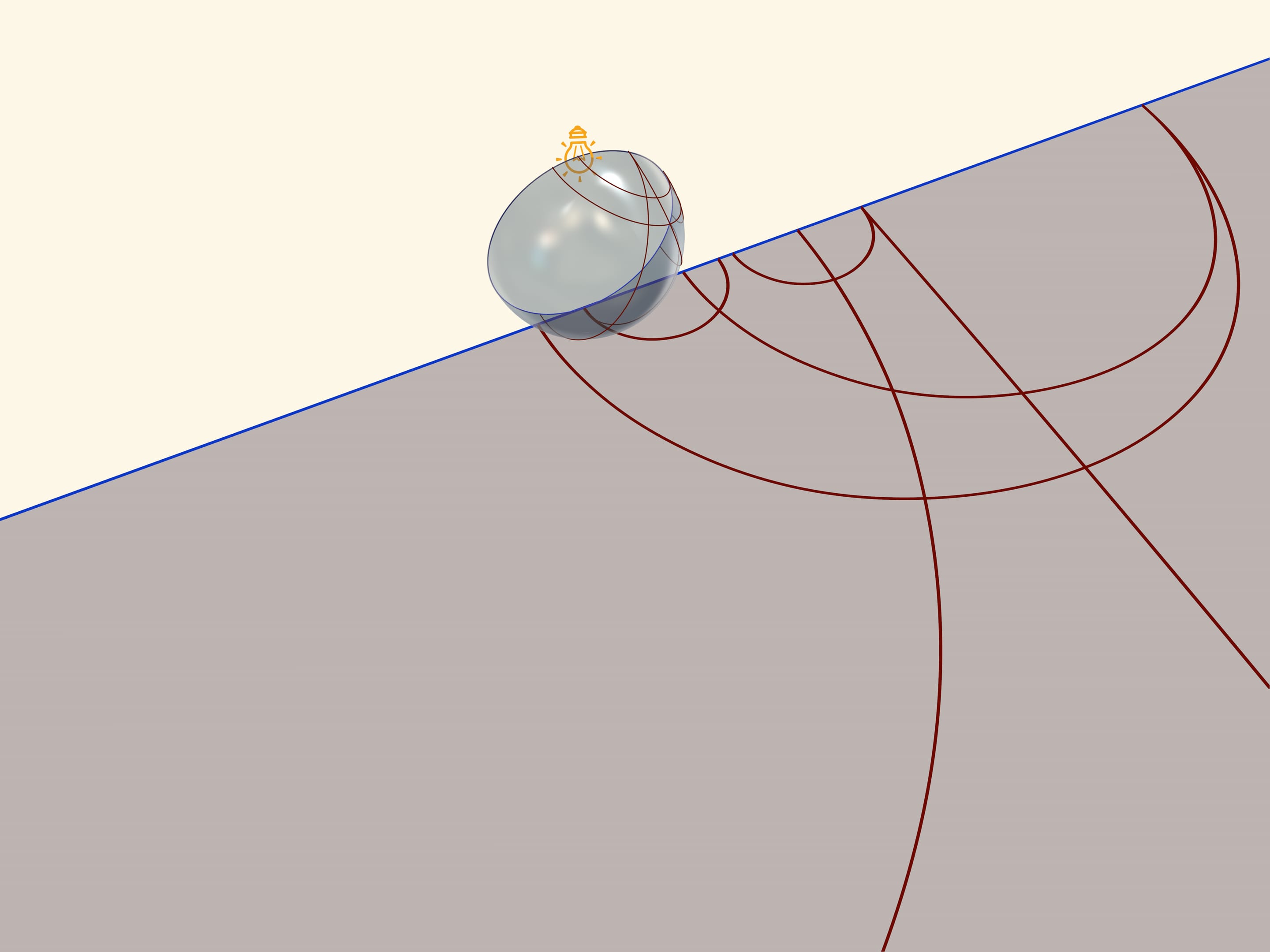
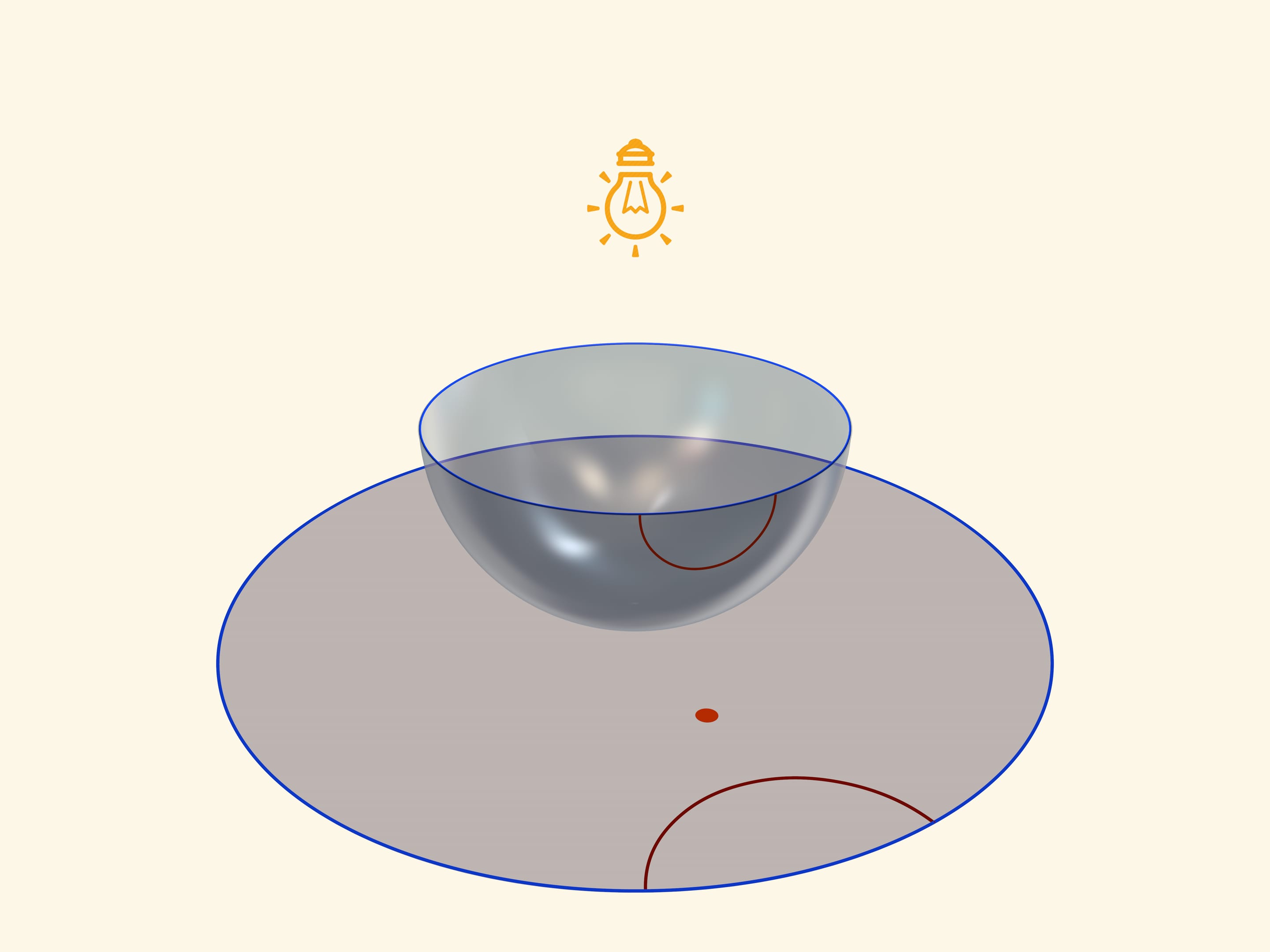
Единой основой, прообразом всех трёх моделей плоскости Лобачевского будет служить прозрачная полусфера с нарисованными на ней полуокружностями, перпендикулярными её границе — экватору. Таким образом, если экватор полусферы лежит в горизонтальной плоскости, то окружности следует проводить в вертикальных плоскостях.
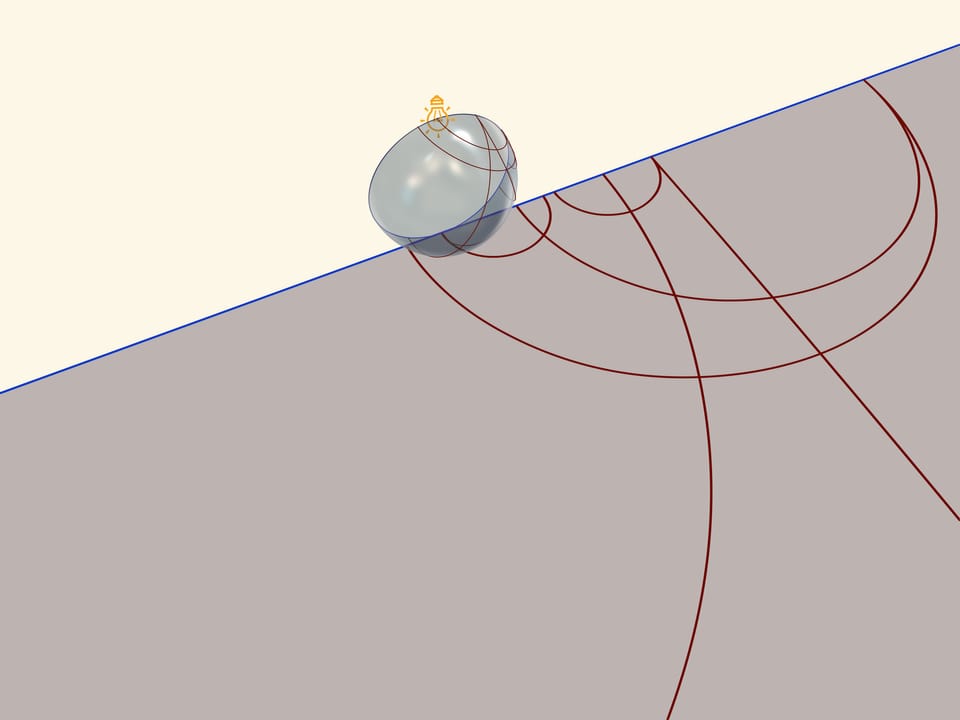
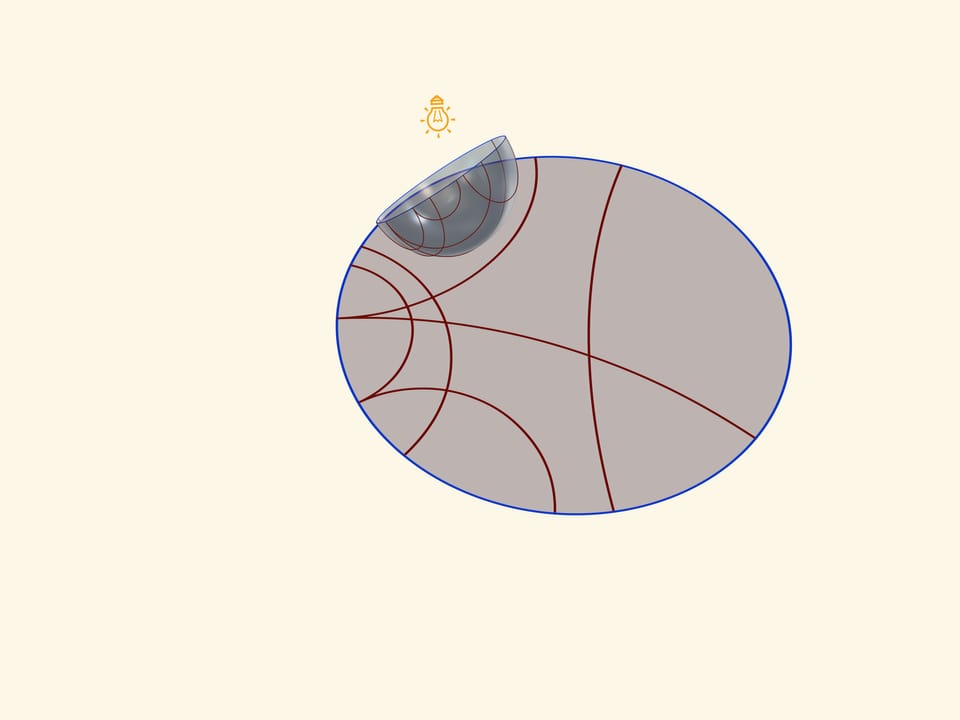
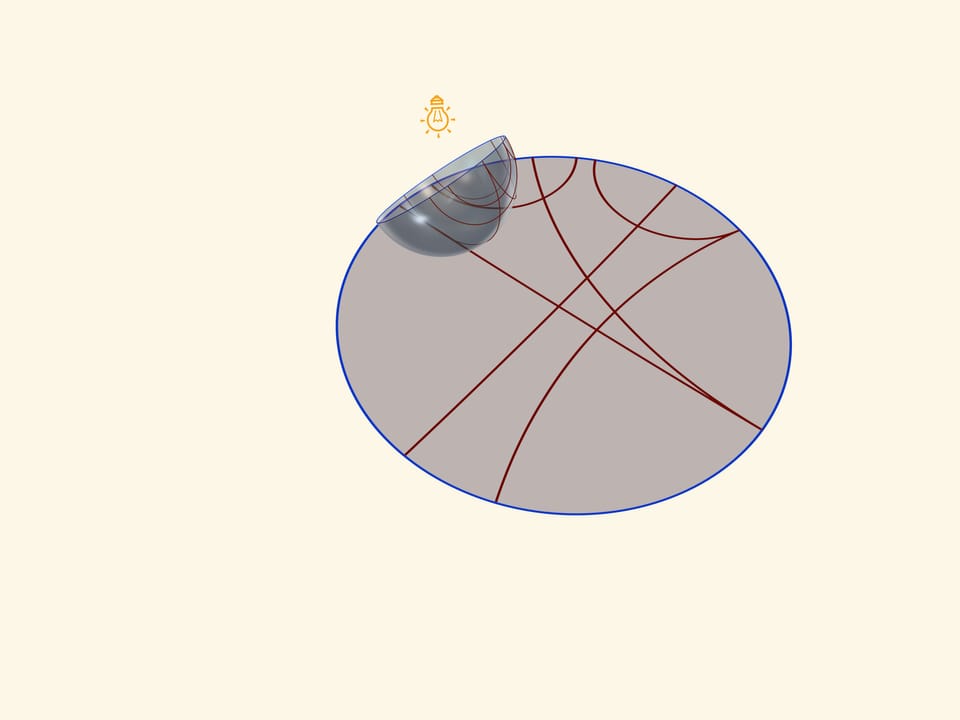
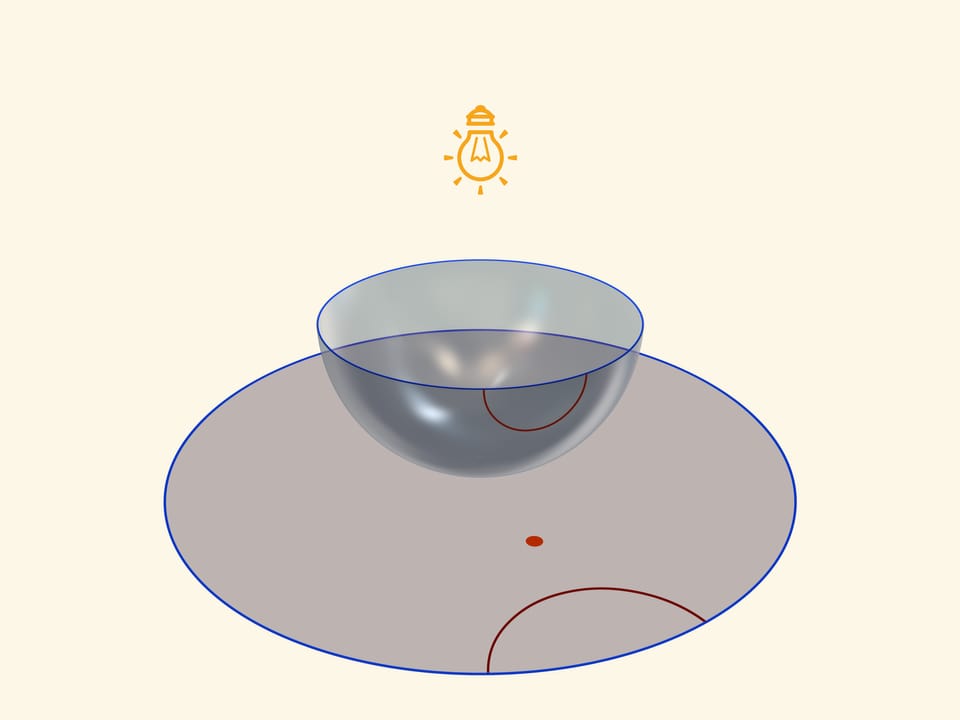
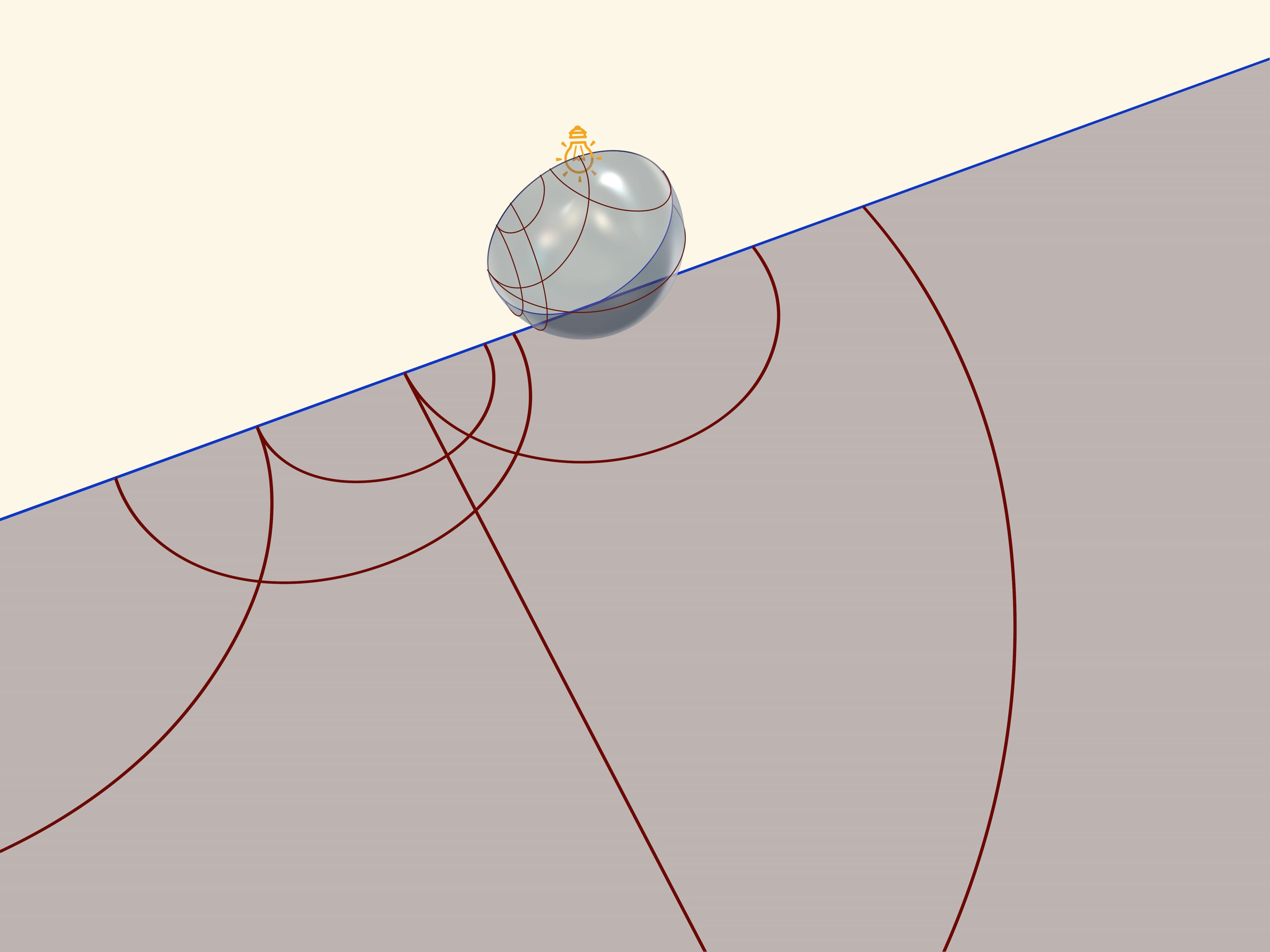
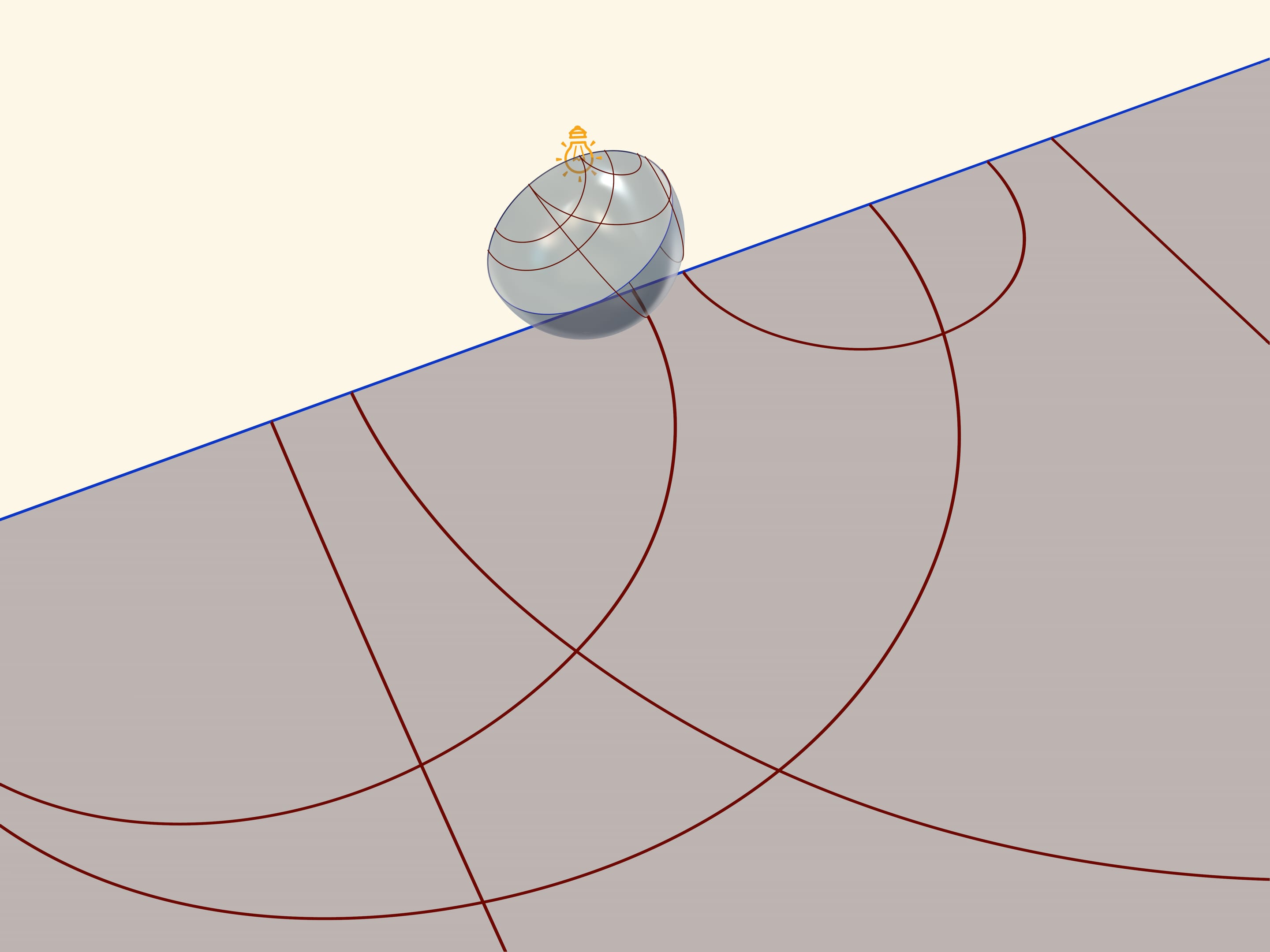
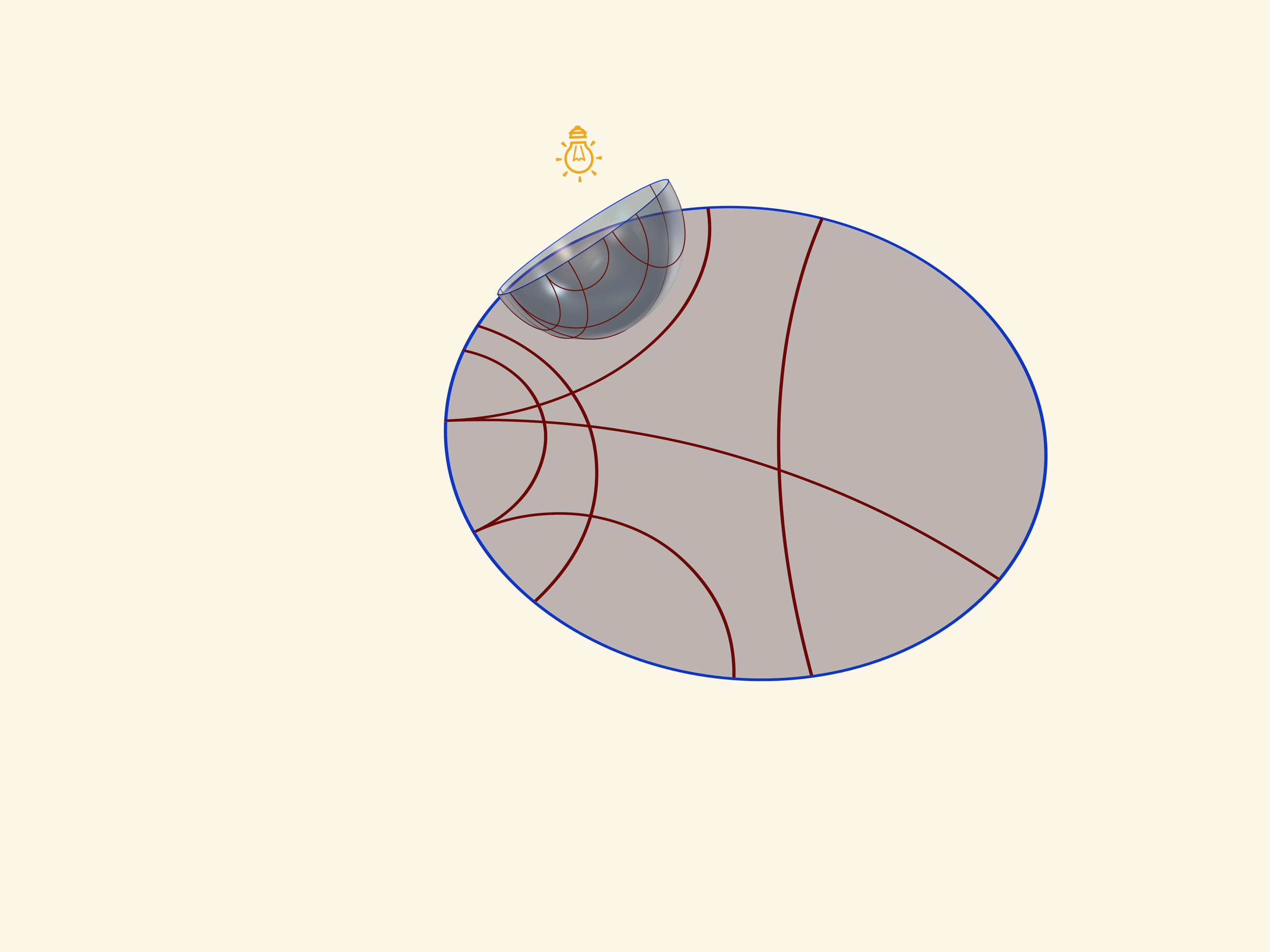
Модель Пуанкаре в круге можно получить, если полусферу поставить на стол полюсом, а точечный источник света поместить в противоположный, северный полюс сферы. Считая, что источник точечный, т. е. лучи от него расходятся по прямым в разные стороны, получается стереографическая проекция сферы (в нашем случае — полусферы) на плоскость. Стереографическая проекция сохраняет углы между линиями, а любые окружности на сфере переводит в окружности на плоскости. (Точнее, окружности, не проходящие через центр проекции, переходят в окружности на плоскости, а проходящие через него — в прямые.)
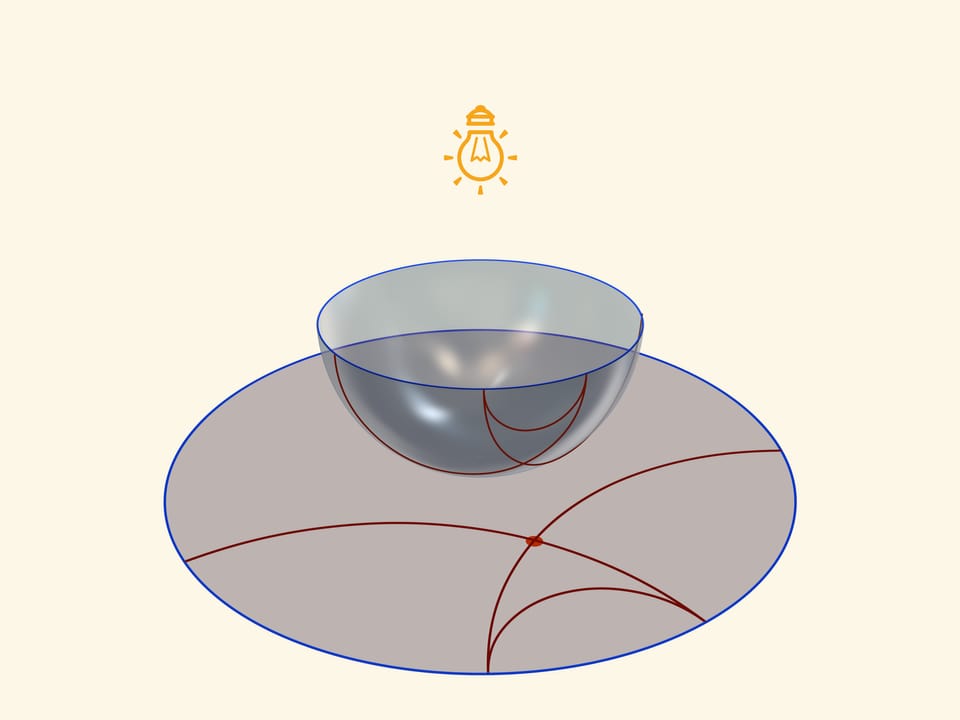
Экватор полусферы переходит в абсолют плоскости Лобачевского (его точки не принадлежат ей), который является границей модели Пуанкаре в круге. Окружности на полусфере, перпендикулярные экватору, переходят в окружности на круге, перпендикулярные абсолюту. Это и есть «прямые» на плоскости Лобачевского.
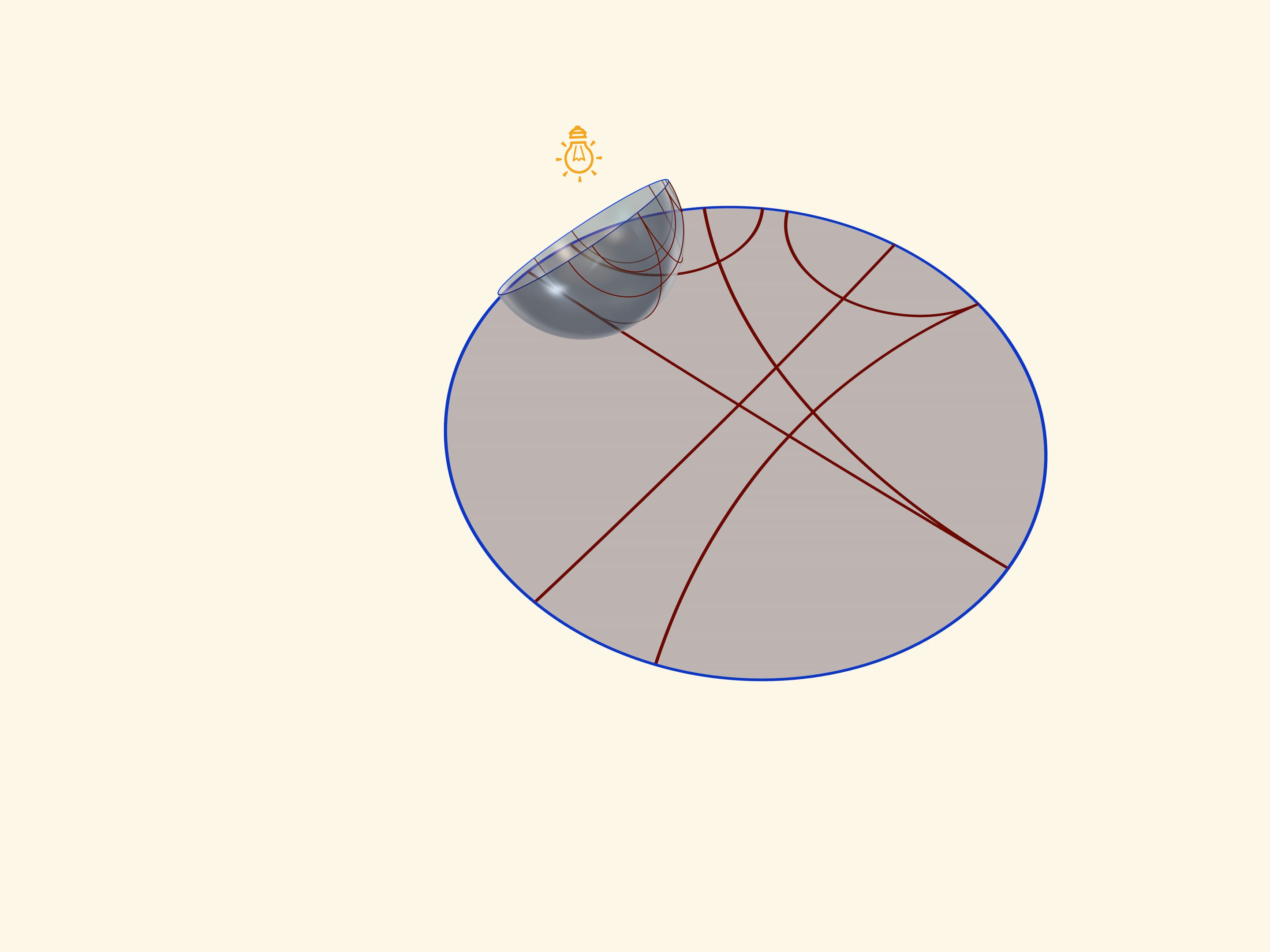
Модель Бельтрами—Клейна в круге (проективная модель) получится, если при таком же положении полусферы источник света «угнать на бесконечность», т. е. освещать полусферу вертикальными параллельными лучами. Абсолютом будет проекция экватора, а прямыми плоскости Лобачевского — хорды круга.
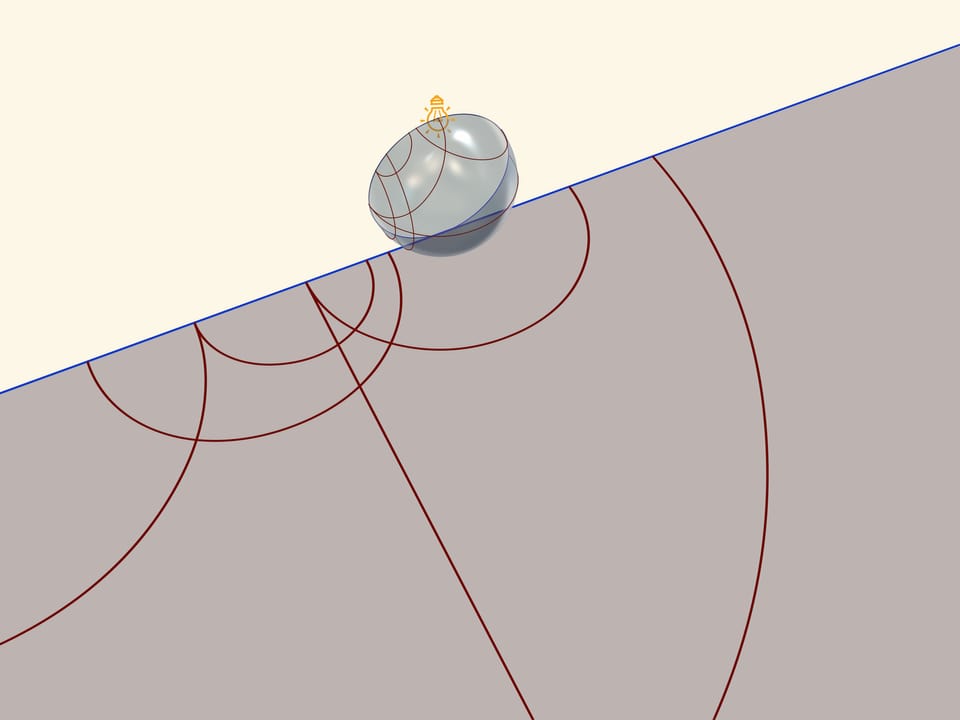
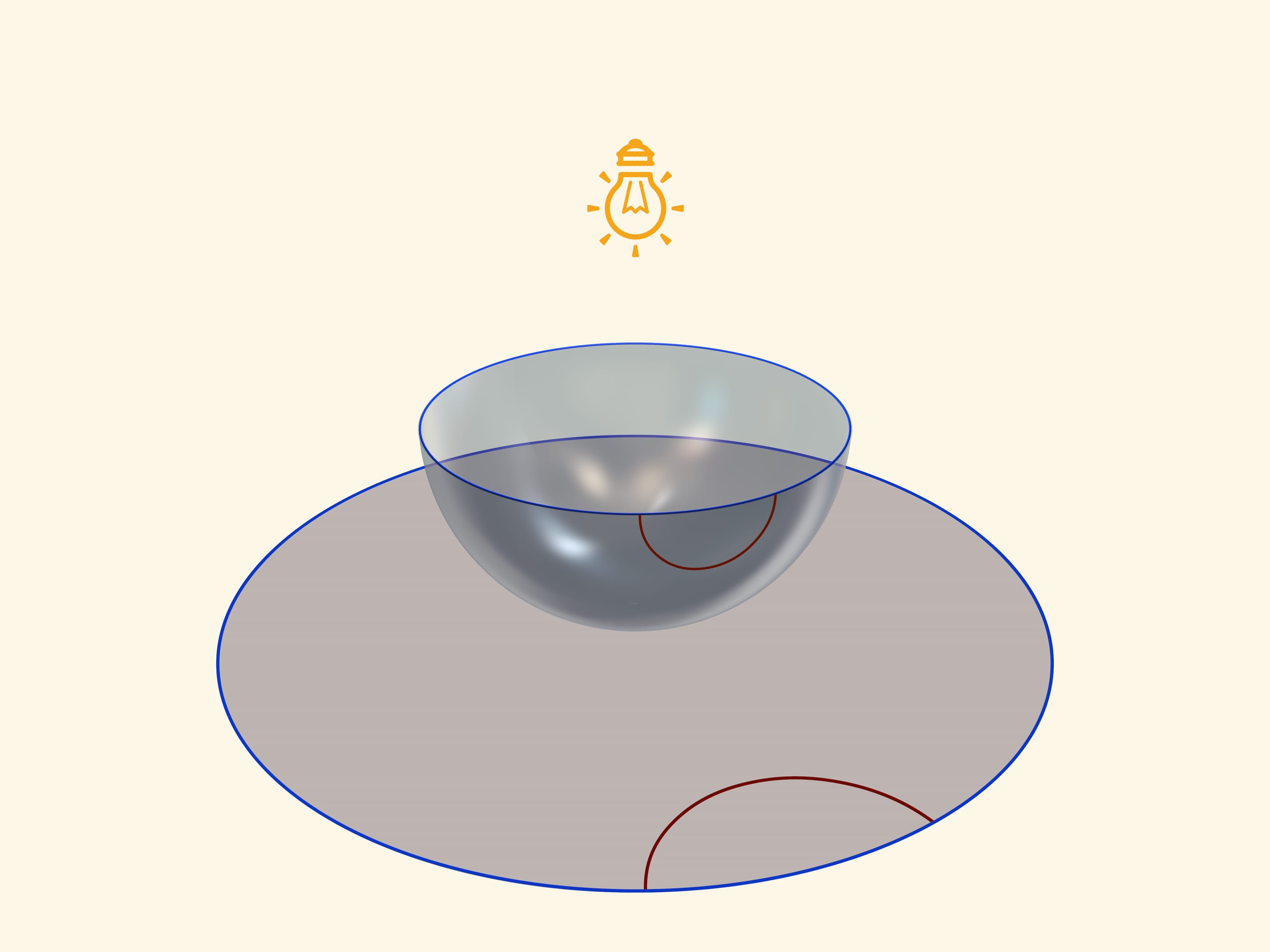
Модель Пуанкаре на полуплоскости можно получить, если полусферу поставить на стол так, чтобы её экватор был в вертикальной плоскости, а точечный источник света поместить в «северный» полюс. Снова возникает стереографическая проекция, при которой полусфера проецируется в полуплоскость, а экватор полусферы переходит в прямую — абсолют плоскости Лобачевского в данной модели. Прямыми в модели Пуанкаре на полуплоскости будут перпендикулярные абсолюту окружности и перпендикулярные абсолюту прямые — проекции с полусферы окружностей, проходящих через северный полюс.
Преобразования (движения) плоскости Лобачевского можно наблюдать, если вращать полусферу. В случае модели Пуанкаре на полуплоскости полусферу следует вращать вокруг оси (так, чтобы экватор всегда находился в одной и той же плоскости). Преобразования (для искушённых читателей — эллиптические) плоскости Лобачевского в случае модели Пуанкаре в круге можно наблюдать, если вращать полусферу вокруг оси, наклонив её к вертикали, соединяющей источник света и точку касания полусферы с плоскостью проекции. (При таком положении полусферы снова получается стереографическая проекция. Её перечисленные свойства гарантируют, что и в этом случае получается модель Пуанкаре в круге.)
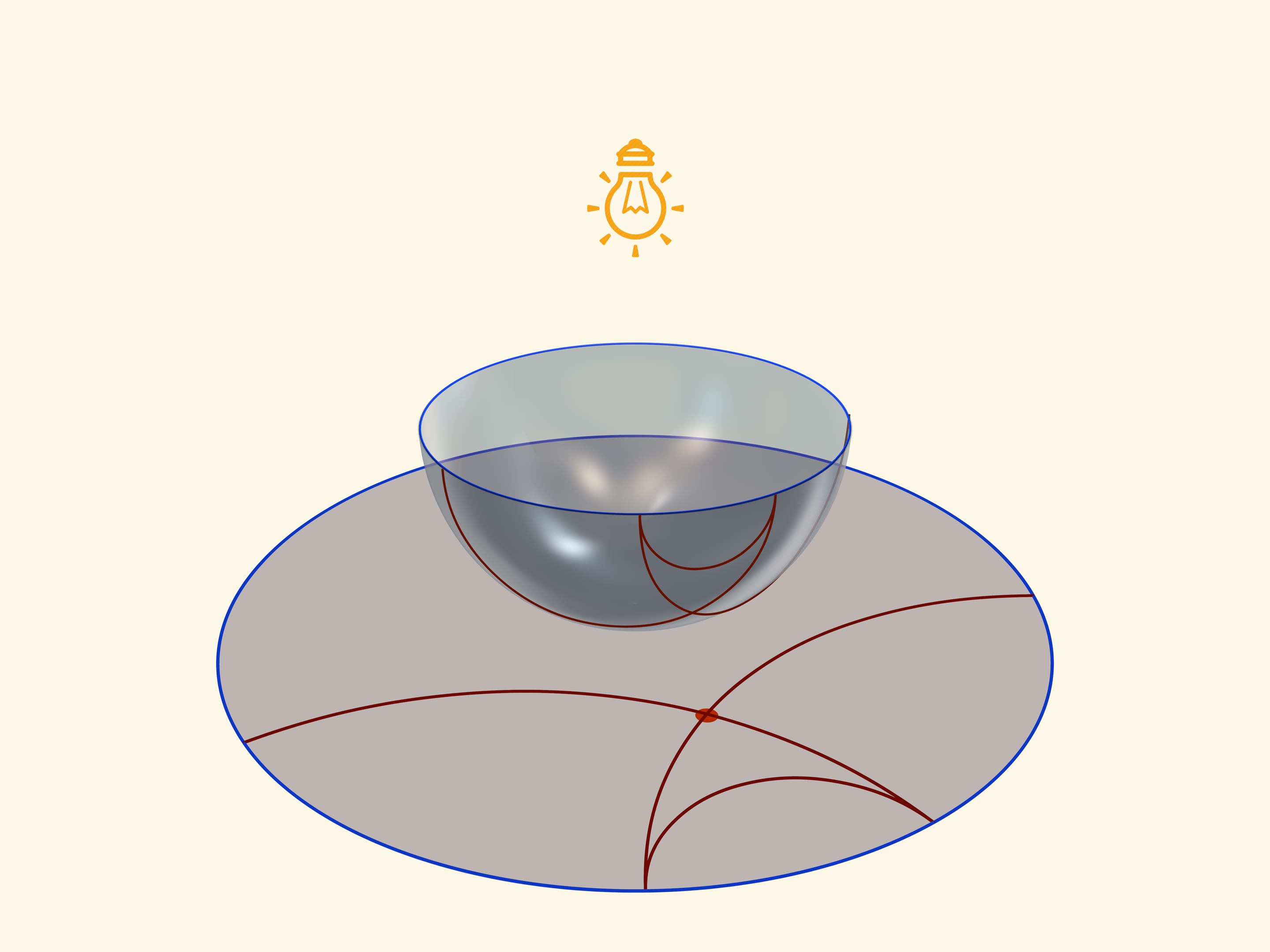
Прямые плоскости Лобачевского, проходящие через одну точку и параллельные данной прямой, наглядно строятся в модели Пуанкаре в круге. Для фиксированной окружности на полусфере, для выбранной точки следует провести две окружности, «исходящие из разных концов» фиксированной. Так как проводятся только окружности, перпендикулярные экватору, их проекции — прямые плоскости Лобачевского — выходят из «общих» точек на абсолюте перпендикулярно ему (напомним, что точки абсолюта не входят в плоскость Лобачевского). А это и значит, что каждая из вновь построенных прямых параллельна фиксированной. А любая прямая, проходящая через выбранную точку и лежащая «между» построенными, называется «расходящейся» с данной и тоже не имеет с ней общих точек.
Литература
Делоне Б. Н. Краткое изложение доказательства непротиворечивости планиметрии Лобачевского. — М. : Изд-во АН СССР, 1953. — [Глава V. Модель Пуанкаре (в круге) плоскости Лобачевского. Стр. 110—116].
Сосинский А. Б. Об эквивалентности трёх моделей плоскости Лобачевского // Математическое просвещение. — 2020. — Вып. 25. — Стр. 38–47.