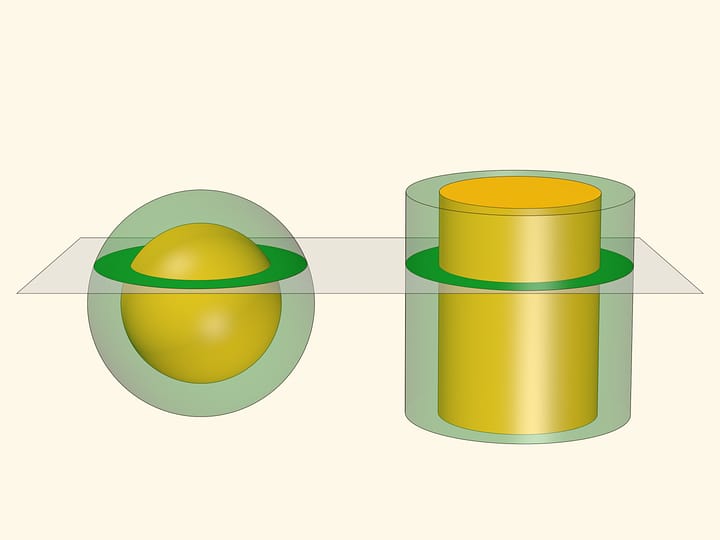
Житейское понимание площади поверхности как количества краски (ткани), необходимого чтобы поверхность покрасить тонким слоем (покрыть), не так-то просто формализовать геометрически… Длина дуги кривой определяется как предел периметров вписанной в дугу ломаной — при условии, что длины всех её сторон стремятся к нулю. В случае кривой поверхности естественно было бы вписывать многогранную поверхность и брать предел её площади при измельчении, но в конце XIX века Герман Шварц придумал поучительный пример.
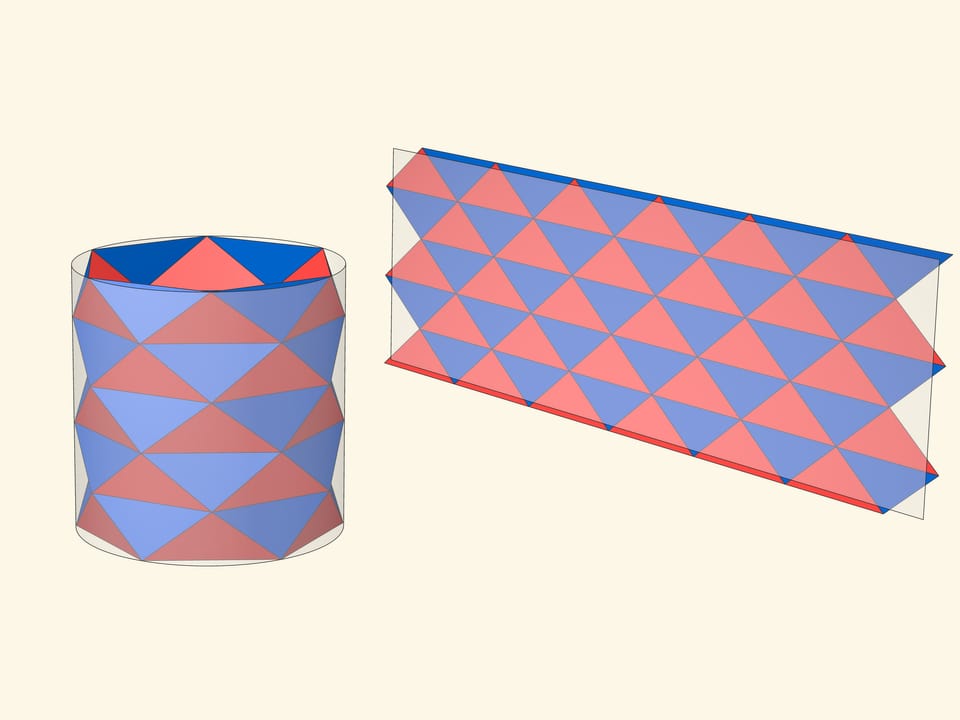
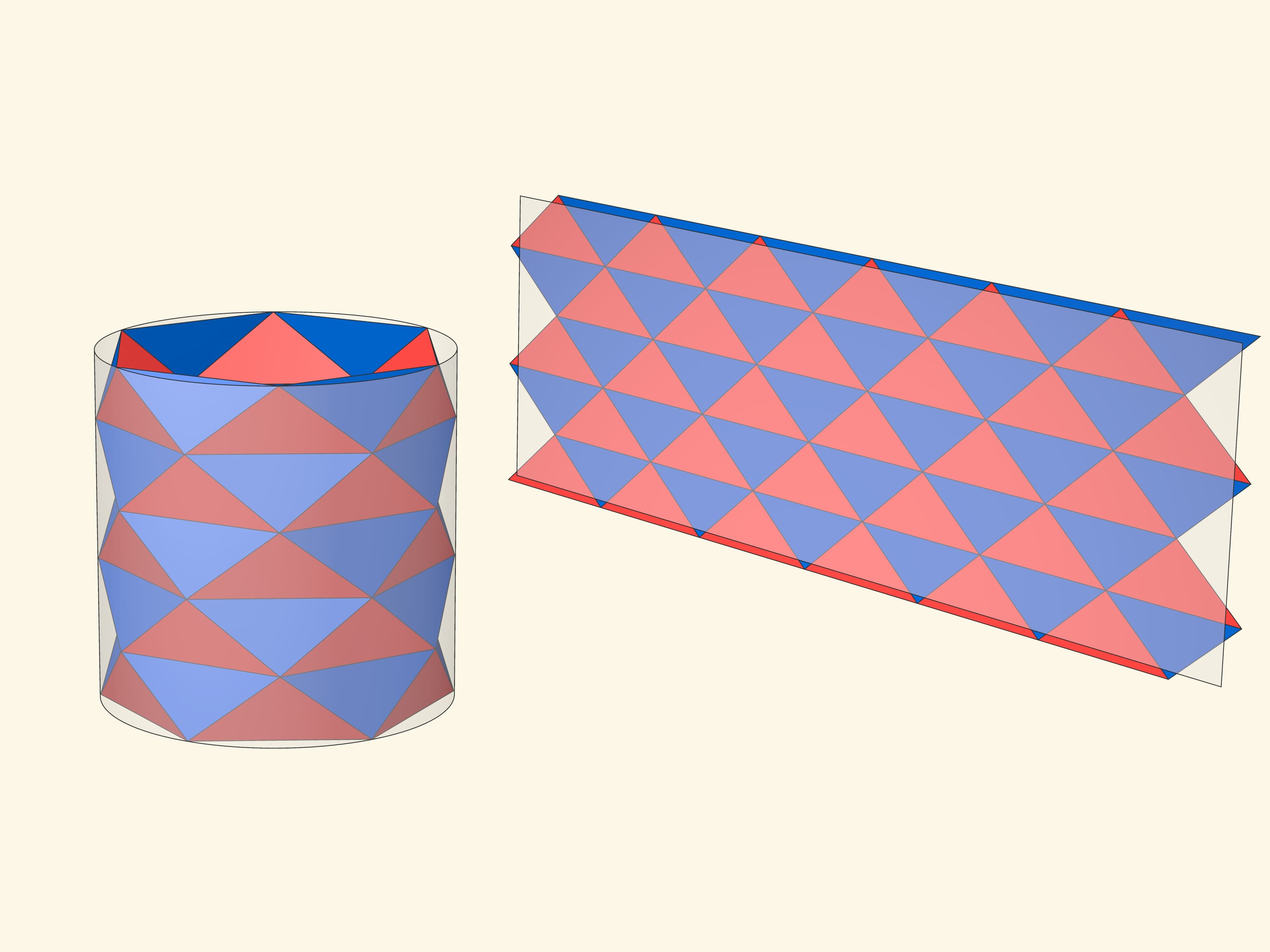
Сапог (в англоязычной литературе — фонарь) Шварца показывает, что даже для такой простейшей поверхности как цилиндр, площадь которой элементарно считается развёртыванием, указанная идея не работает. Цилиндр разбивается равномерно по высоте $n$ горизонтальными окружностями, в каждую из которых вписывается правильный $k$-угольник. Многоугольники поворачиваются друг относительно друга на угол $\pi /k$, а их вершины объединяются в треугольники: каждый слой является антипризмой.
Если при фиксированном количестве слоёв увеличивать количество углов $k$ в многоугольниках, то поверхность сапога будет приближаться к поверхности цилиндра.
Если оставлять количество углов фиксированным, а увеличивать количество уровней $n$ то площадь можно сделать сколь угодно большой.
И в том, и в другом случае варьировался только один параметр, и общий размер треугольника не уменьшался. Приближение подразумевает, что треугольники будут всё мельче и мельче. Но и это не помогает: если увеличивать оба параметра, то размер треугольников будет уменьшаться, а эффект сохранится. При увеличении $k$ и $n$ так, что количество слоёв растёт быстрее чем квадрат количества углов многоугольника, сумма площадей треугольных граней сапога Шварца стремится к бесконечности.
Существенное различие случая ломаной, вписанной в кривую и многогранной поверхности, вписанной в поверхность, в следующем. Когда хорды вписанной ломаной достаточно малы, то направление каждой из хорд почти совпадает с направлением касательной к кривой. В случае же сапога Шварца касательные плоскости к цилиндру вертикальны, а при выполнении описанного условия треугольники оказываются расположены почти горизонтально.
Интересно, что описанный эффект проявляет себя и в 3D-графике. Поверхности, возникающие в сценах, зачастую заменяются их триангуляциями. А визуализация поверхности, в частности освещённости, зависит от направления нормалей. Как уже понятно, при неудачной триангуляции можно получить нежелательные эффекты.
Литература
Дубровский В. Н. В поисках определения площади поверхности // Журнал «Квант». — 1978. — № 5. — Стр. 31—34.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т. 3. — 5-е изд., стер. — М.: Физматлит, 1966. — Стр. 248—251.
Определение длины пути по карте // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 64.