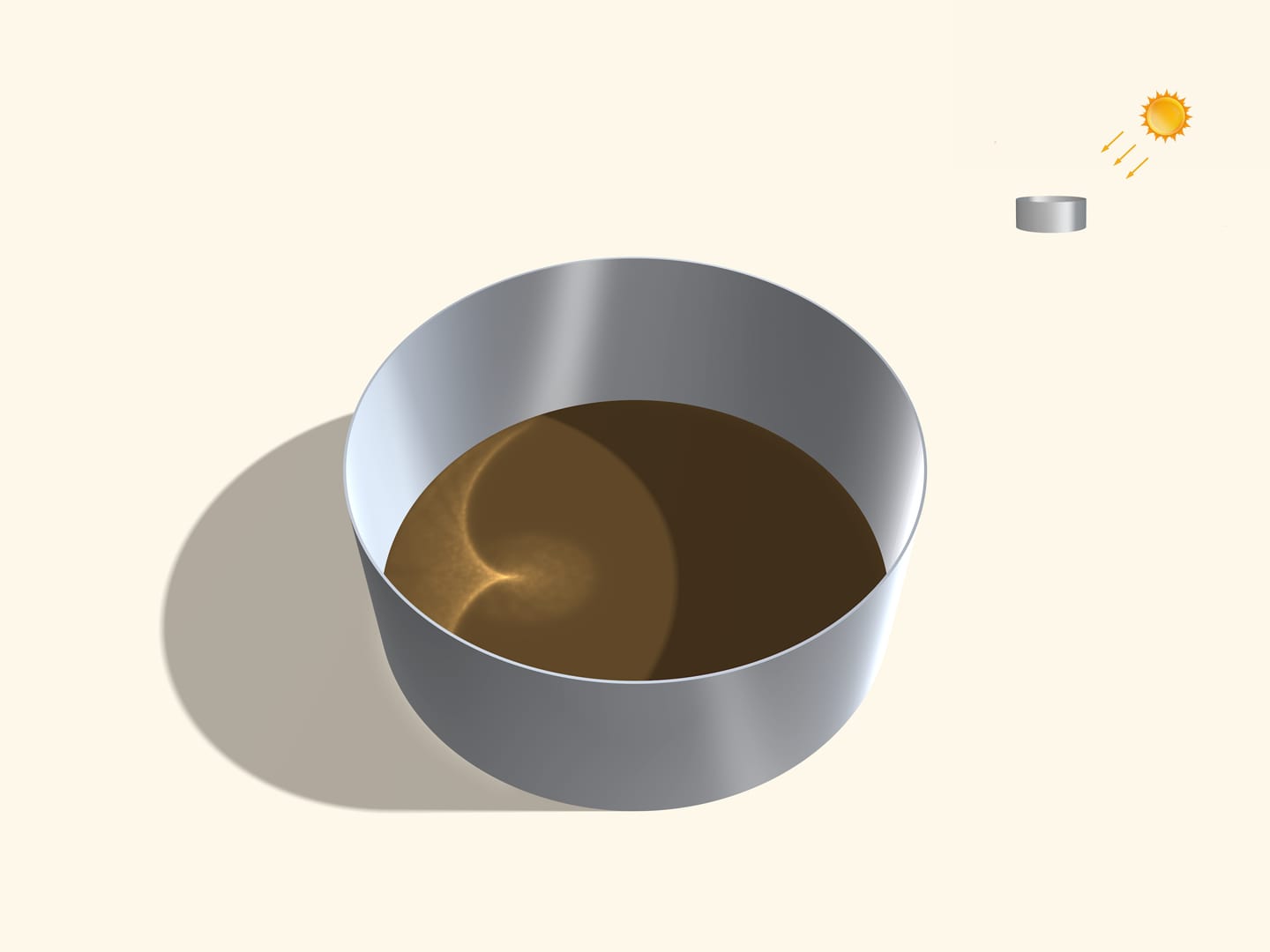
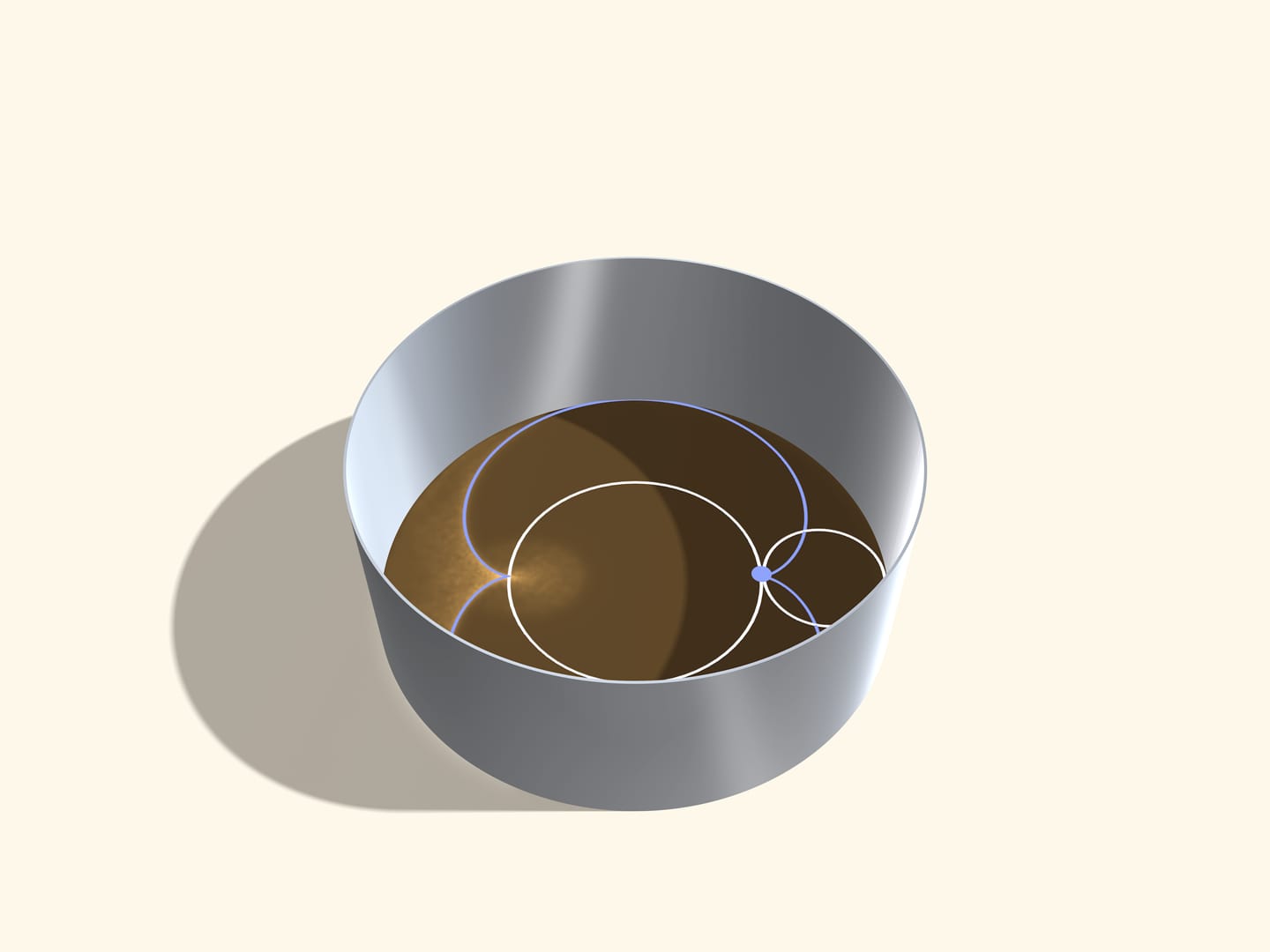
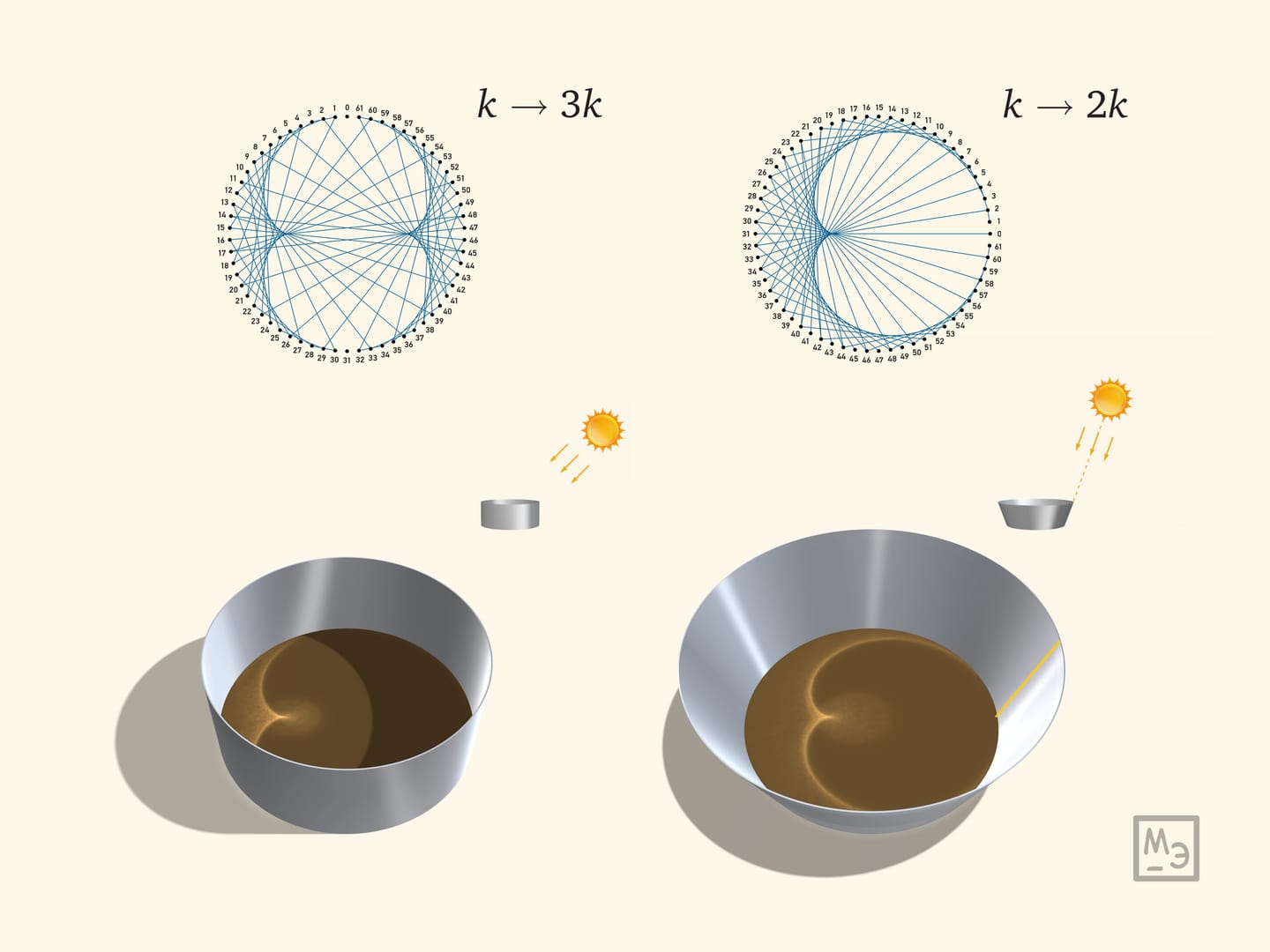
Выйдите в солнечную погоду с чашечкой кофе на свежий воздух. В домашних условиях: возьмите фонарик и посветите в чашку или эмалированную кастрюлю. На дне вы увидите ярко освещённую кривую, называемую каустикой (др.-греч. καύστικος — жгучий). Объяснение этого физического явления основано на математическом понятии «огибающая», подробно описанном в сюжете Парабола: изонить. При отражении от цилиндрической поверхности лучи нарисуют нефроиду, а когда лучи света параллельны одной из образующих конической поверхности — кардиоиду.
В сюжете Кардиоида и нефроида дано определение этих эпициклоид и рассказано, как их «связать» из ниток. Любознательному читателю предлагаем провести эксперимент с чашками, а затем, распечатав на бумаге хорды соответствующие цилиндру и конусу, положить вырезанный круг внутрь посуды и убедиться, что получаются соответствующие кривые. А в этом сюжете постараемся разобраться, как образуются каустики, и почему в цилиндре возникает нефроида, а в конусе — кардиоида.
Параллельные лучи света, падая под углом на поверхность прямого кругового цилиндра, отражаются и на дне дают каустику в виде… к концу сюжета убедимся, что нефроиды, касающейся цилиндра. Отражение происходит от половины цилиндра, и получается половинка нефроиды — кривая с одной особой точкой, по-английски cusp, остриё. Причём положение нефроиды и её особенности не зависит (в разумных пределах) от положения Солнца, а изменение высоты цилиндра влияет только на то, какую часть нефроиды мы видим.
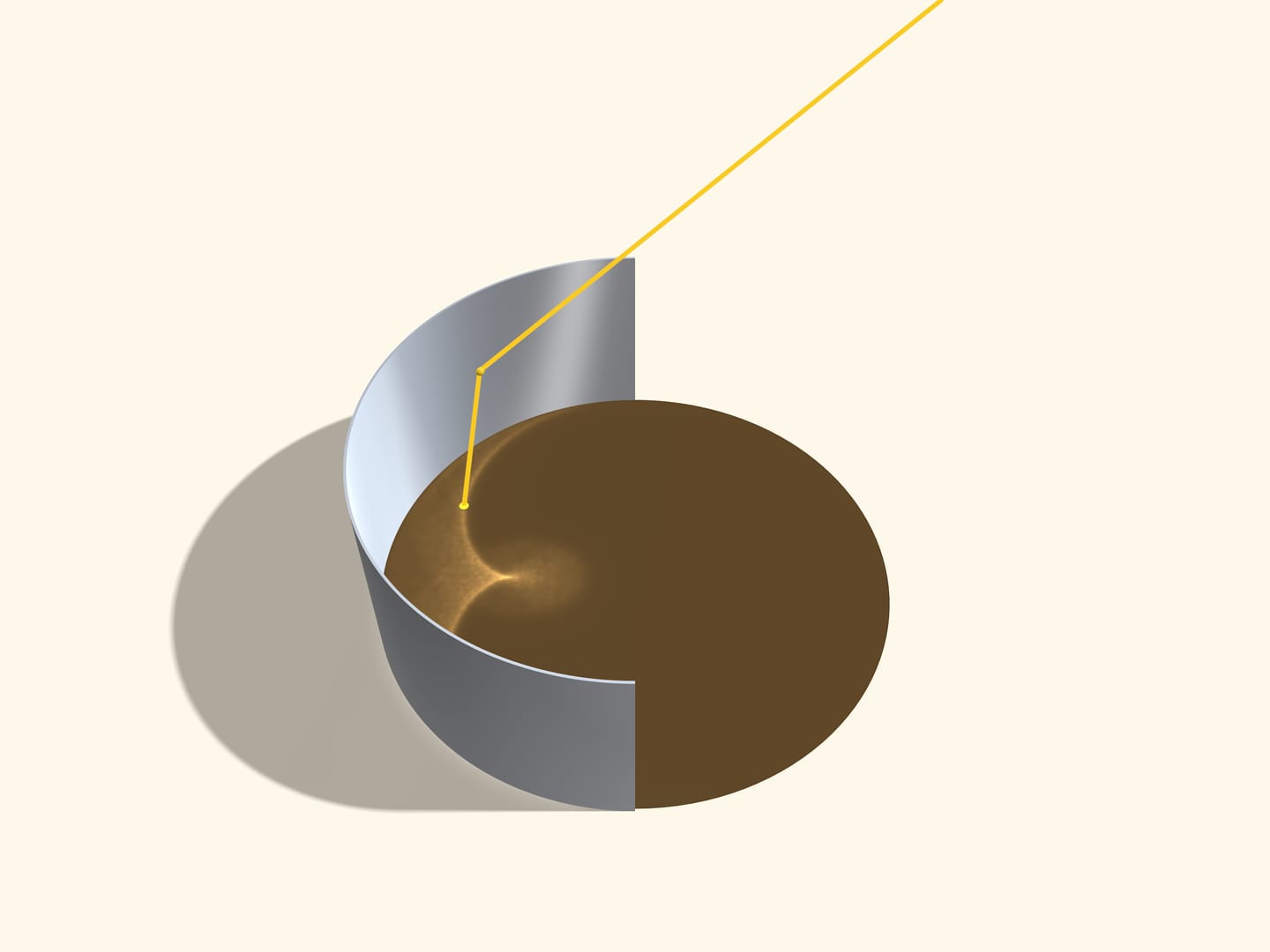
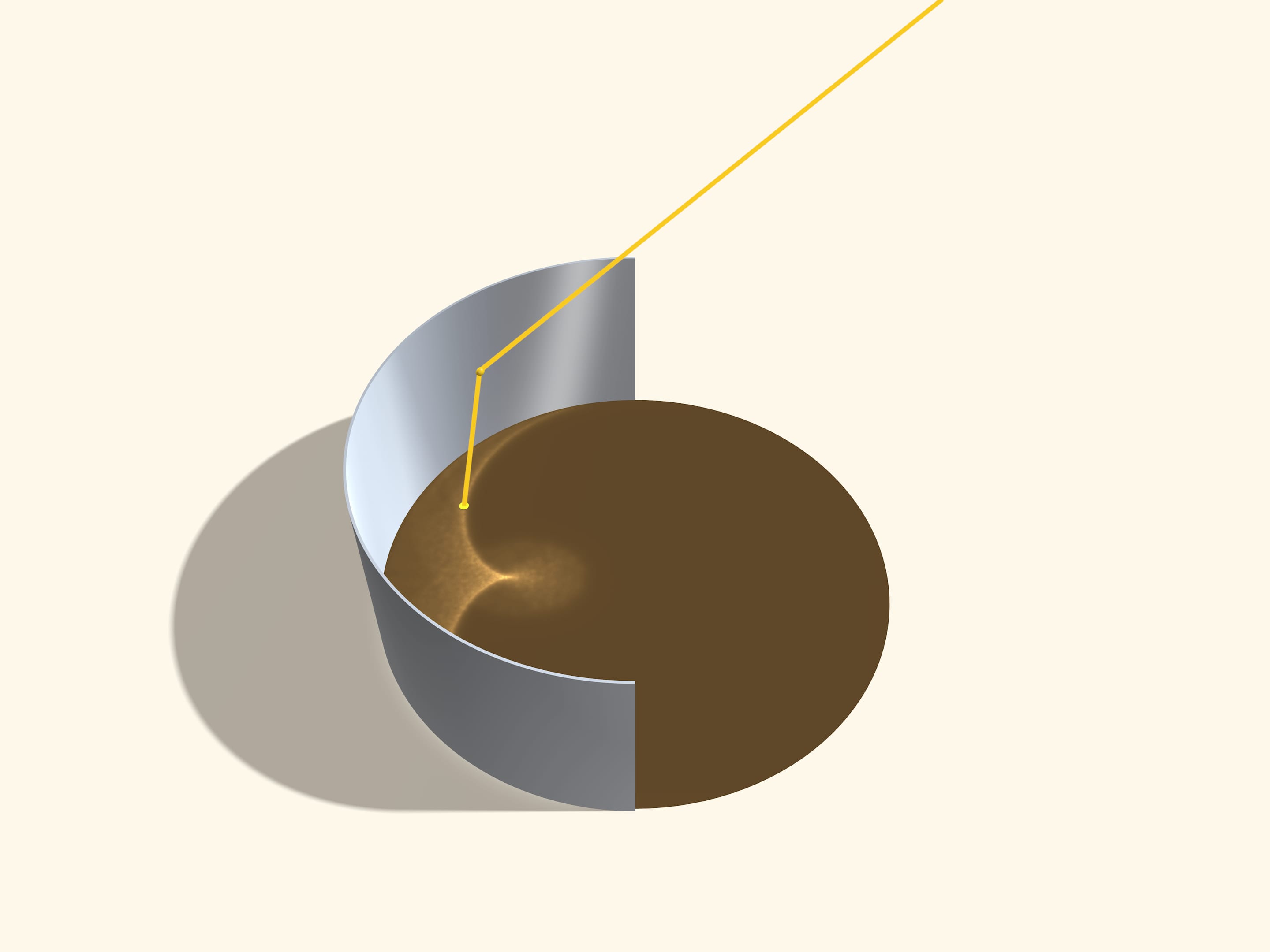
Луч, приходящий «сверху» от Солнца, отражается от внутренней поверхности цилиндра, идёт вниз и, «ударяясь» в кофе, подсвечивает на его поверхности точку. Именно благодаря множеству этих подсвеченных точек мы и видим каустику в виде нефроиды.
Отражение луча определяется касательной плоскостью к поверхности отражения, точнее вектором нормали этой плоскости в точке отражения: отражённый луч уходит в плоскости, «натянутой» на пришедший луч и вектор нормали. Причём в этой плоскости «угол падения равен углу отражения». Поэтому лучи, отражающиеся от одной образующей цилиндра, поточечно подсвечивают на кофе отрезок прямой.
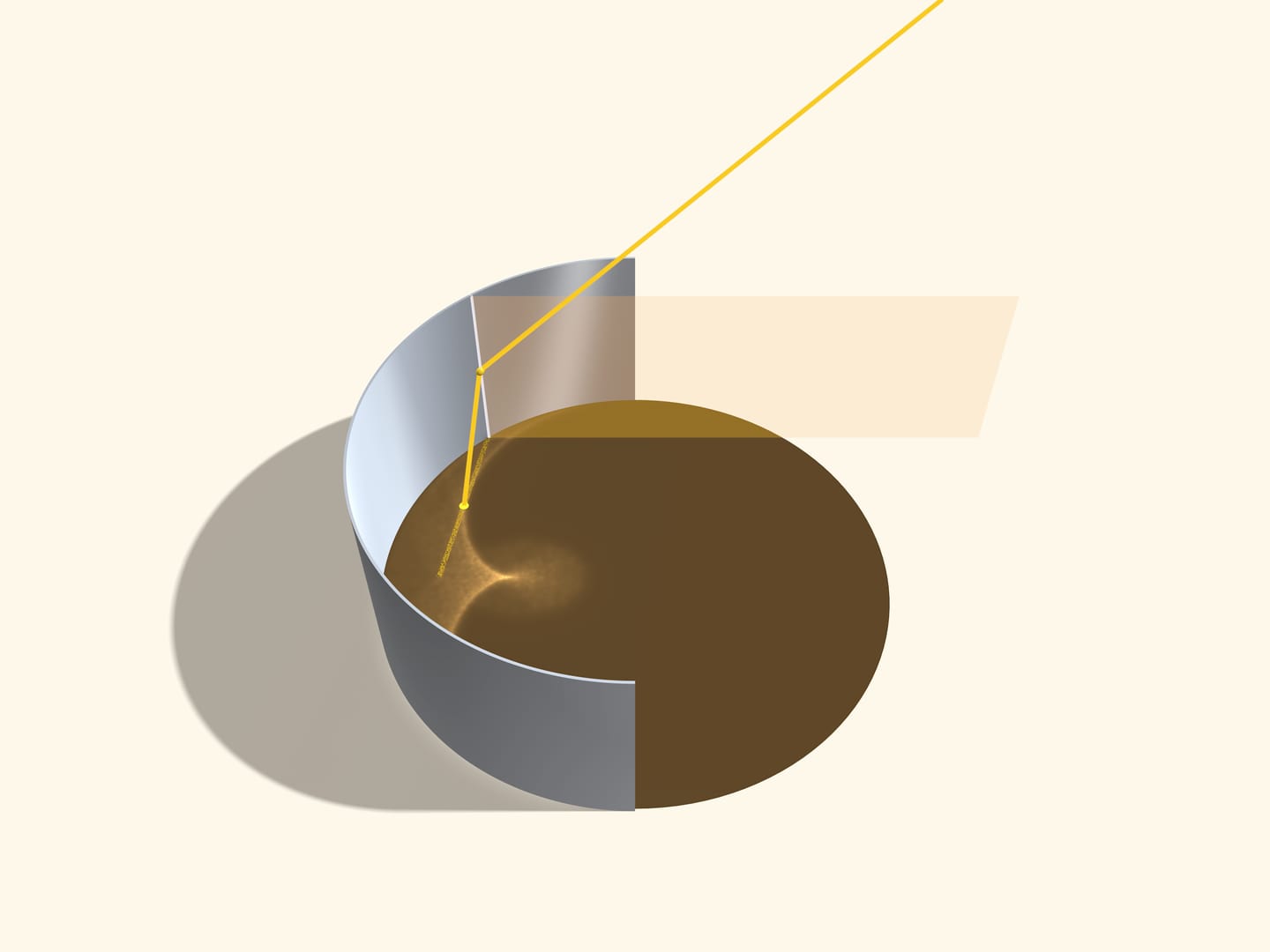
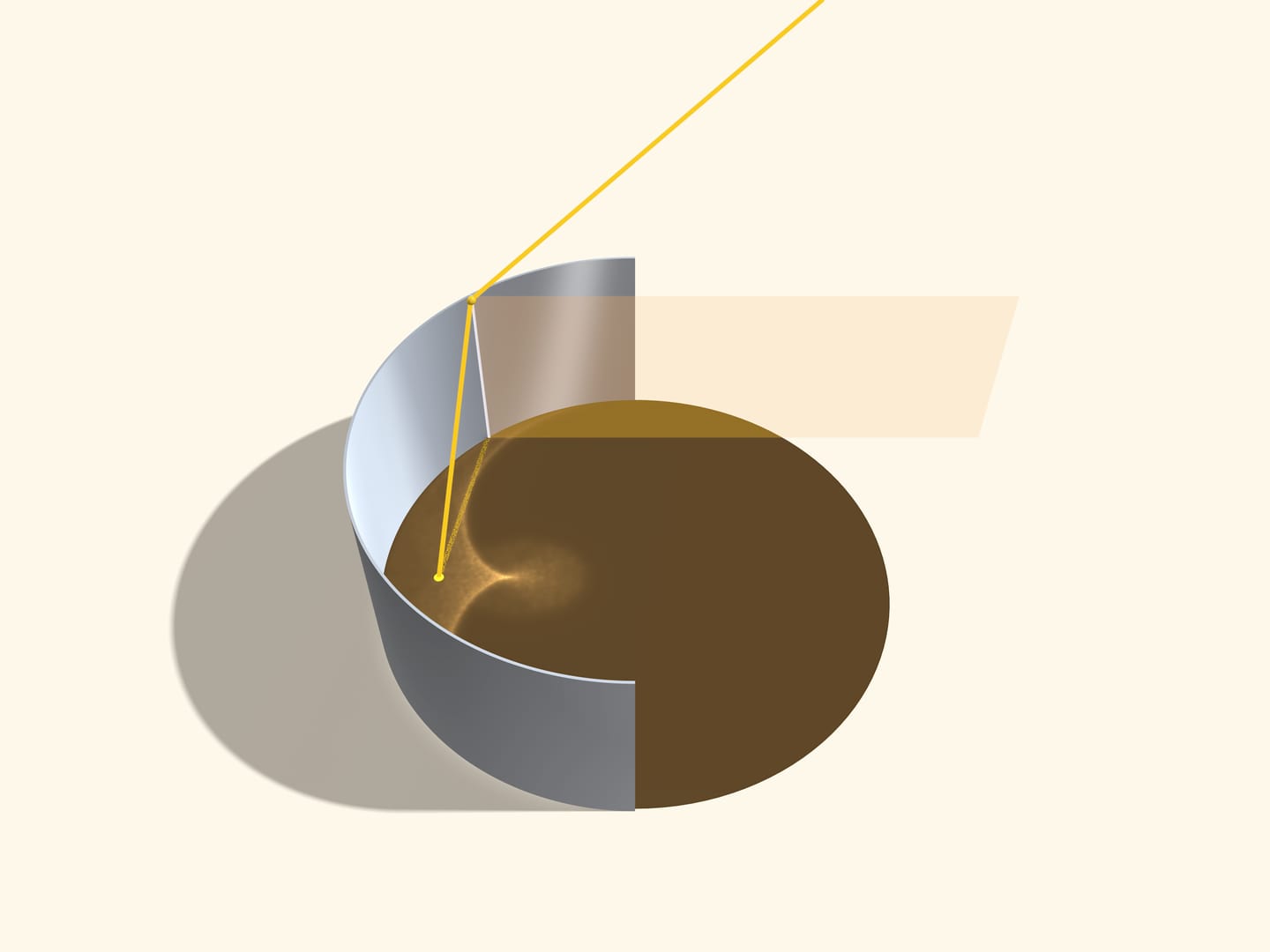
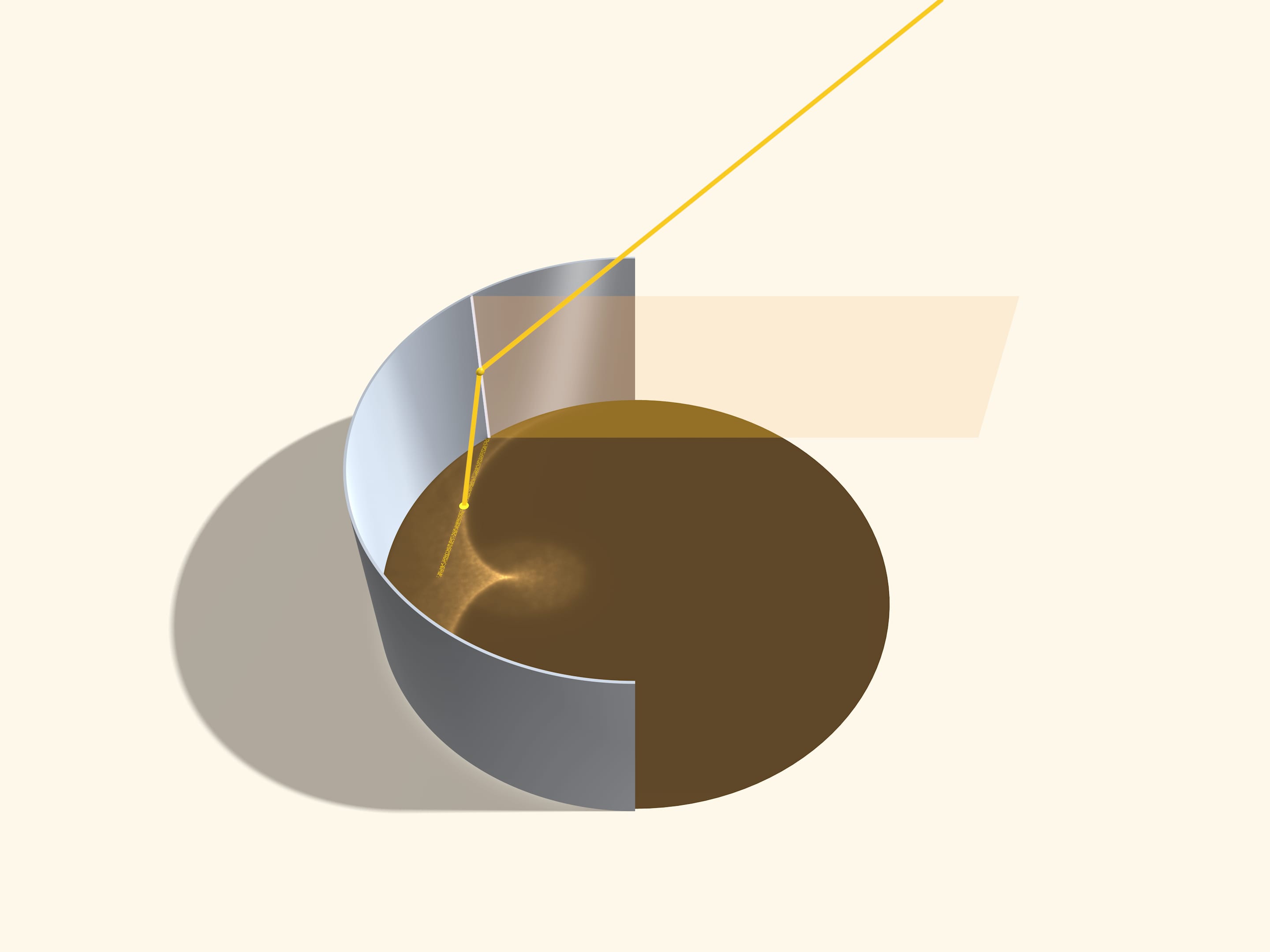
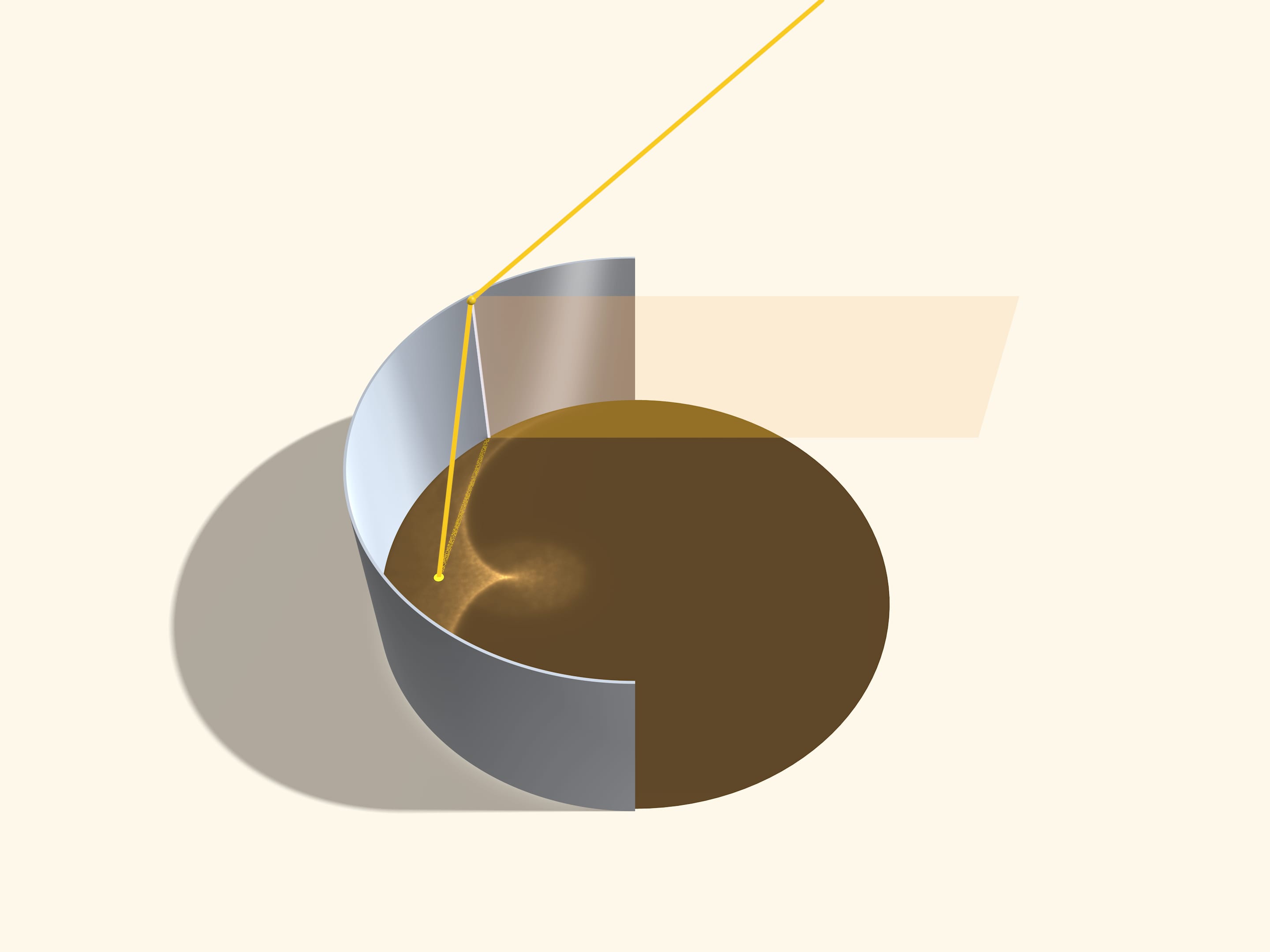
Лучи, отражающиеся от одной образующей цилиндра, лежат в плоскости, содержащей эту образующую (и, соответственно, перпендикулярной поверхности кофе) и направленной в сторону Солнца. Весь приходящий свет как бы «расслаивается» на параллельные плоскости, и каждая такая плоскость подсвечивает на поверхности кофе отрезок хорды. Видимая каустика образуется как огибающая этих хорд. Разберёмся, как они идут.
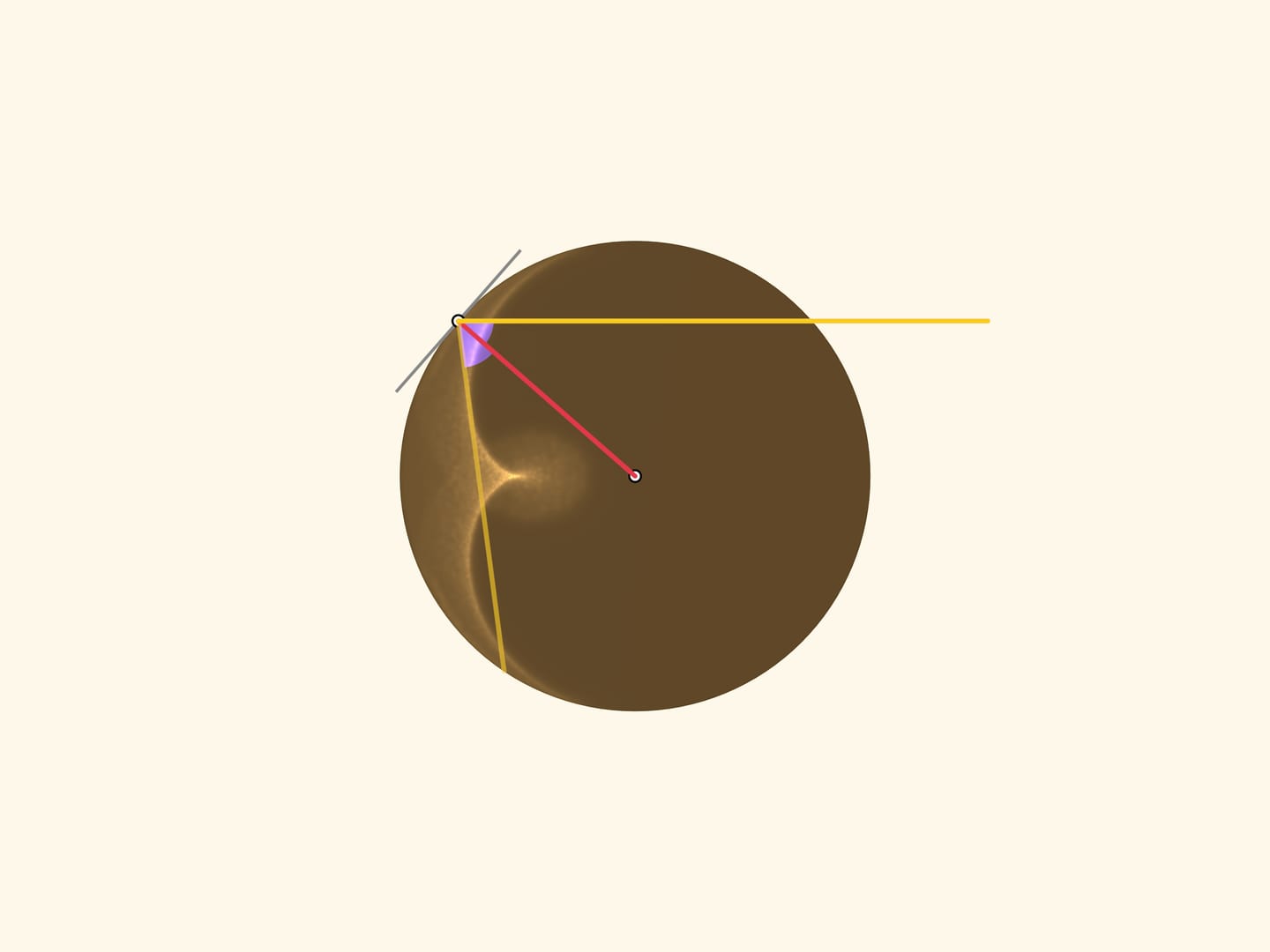
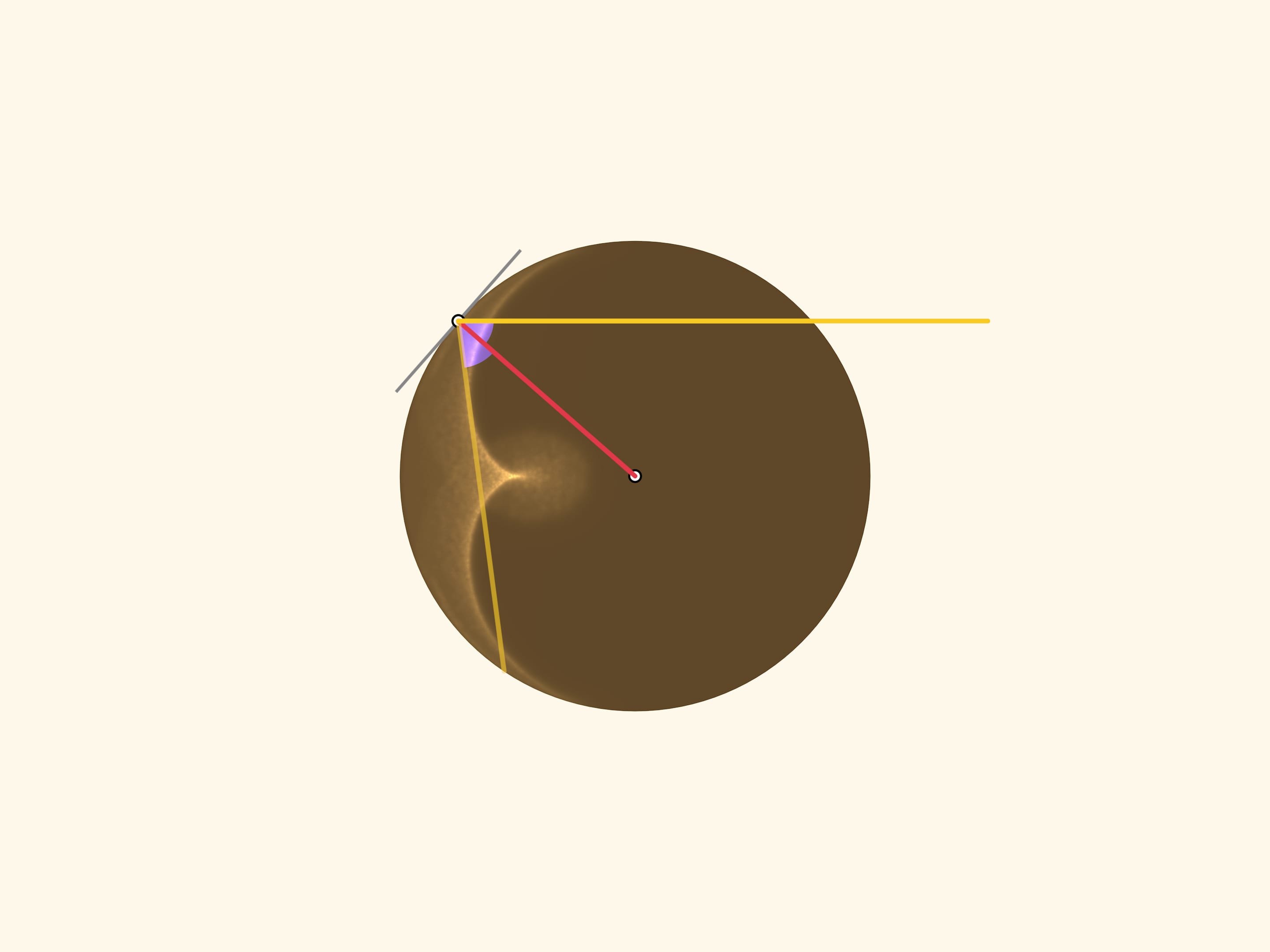
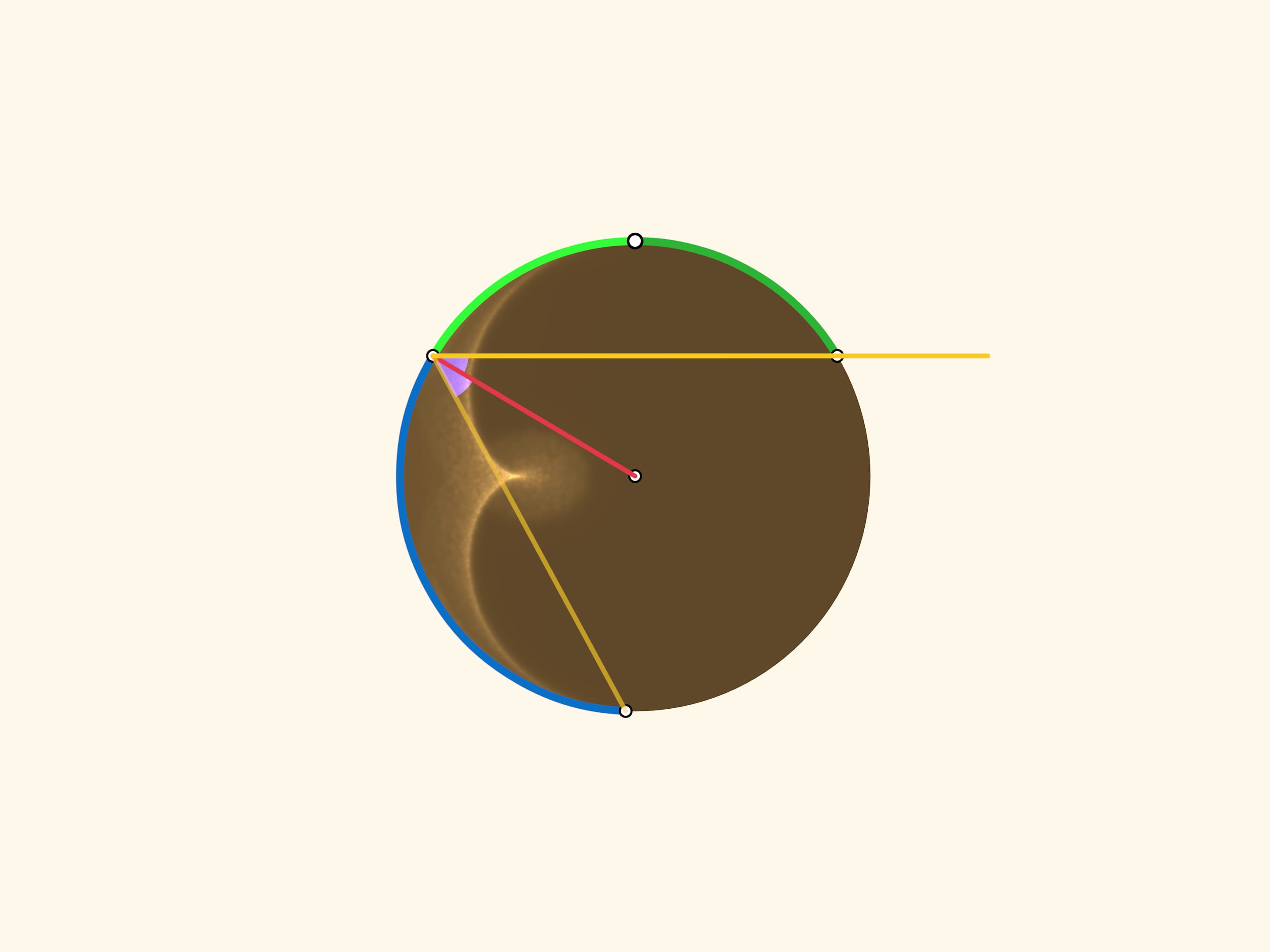
Если посмотреть «сверху», то увидим картинку, появившуюся ещё в конце XVII века в труде Христиана Гюйгенса «Трактат о свете». Плоскость лучей становится одним лучом, приходящим по направлению от Солнца. Отражённый луч уходит под тем же углом относительно радиуса круга, проведённого в точку отражения, что и приходящий. («Спроецируем» равенство углов солнечного и отражённого от цилиндра лучей с вектором нормали.)
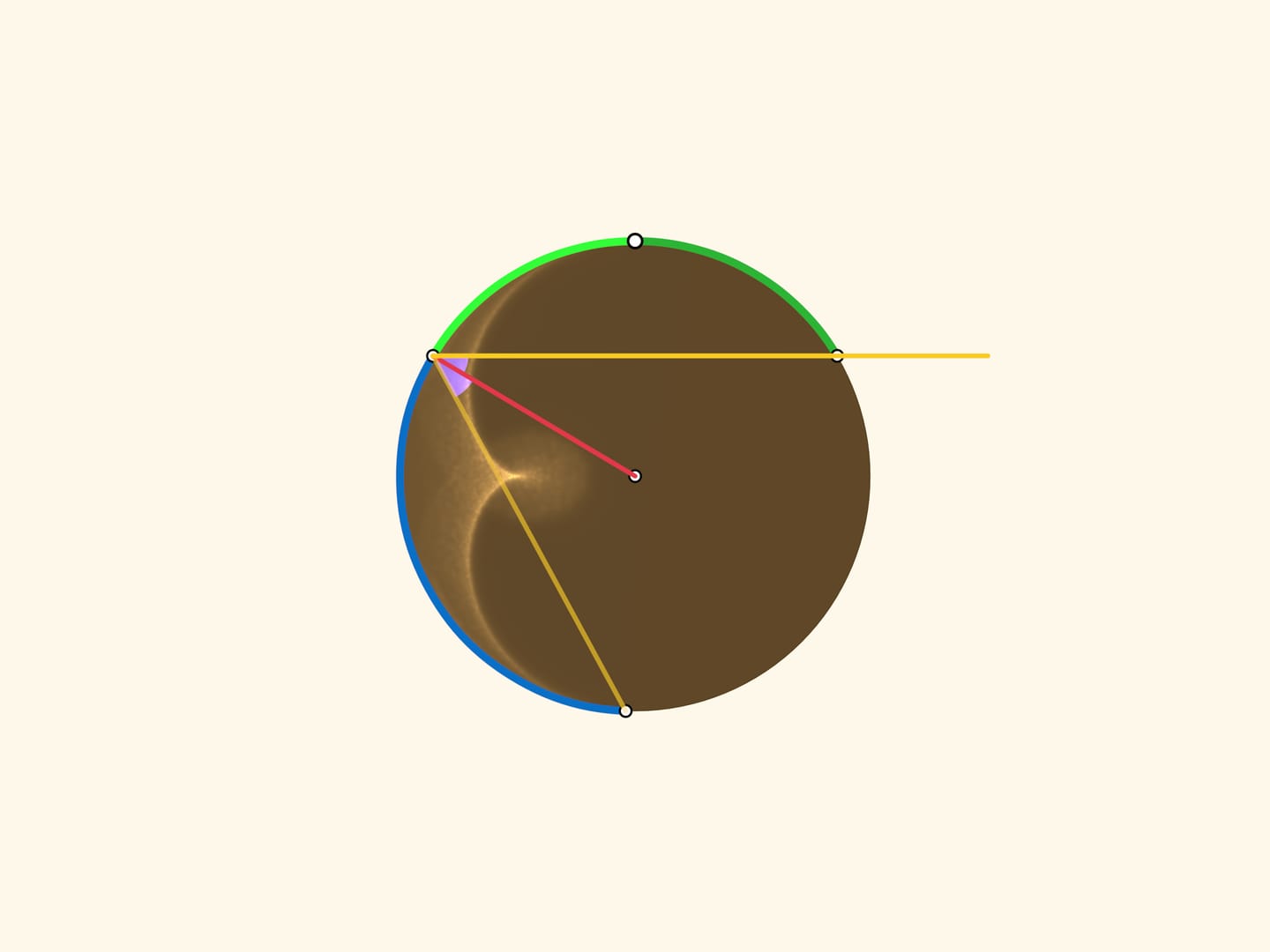
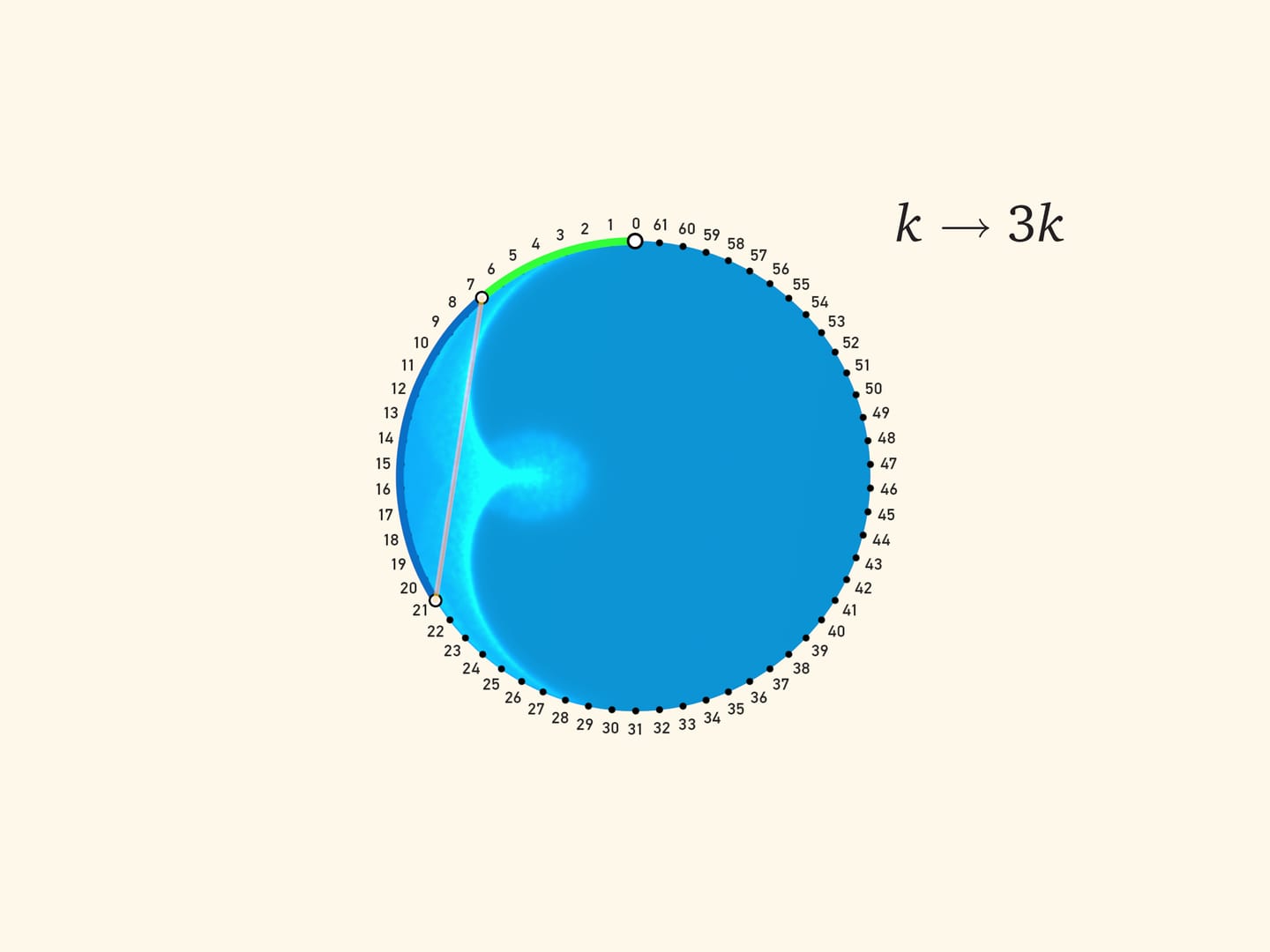
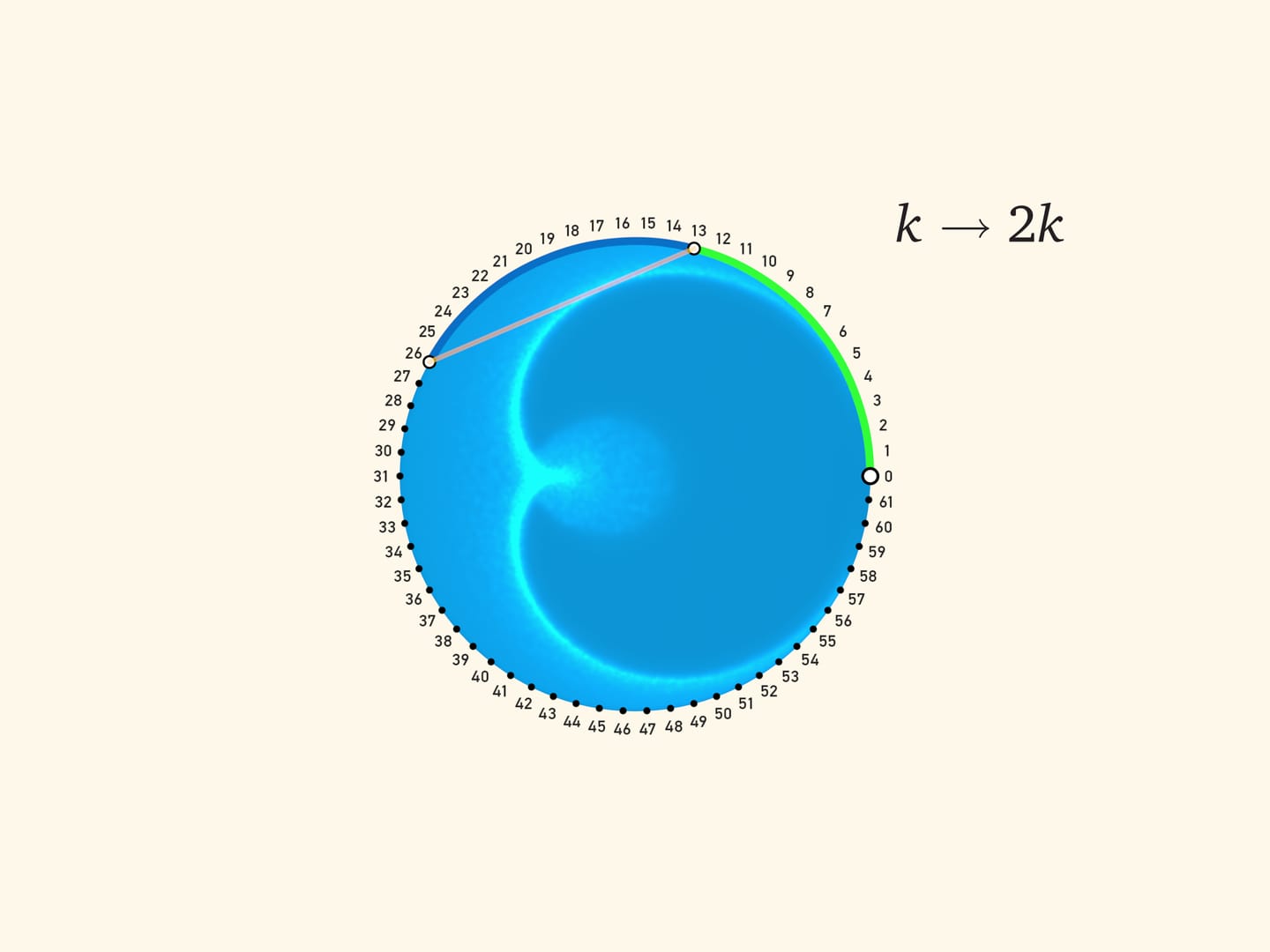
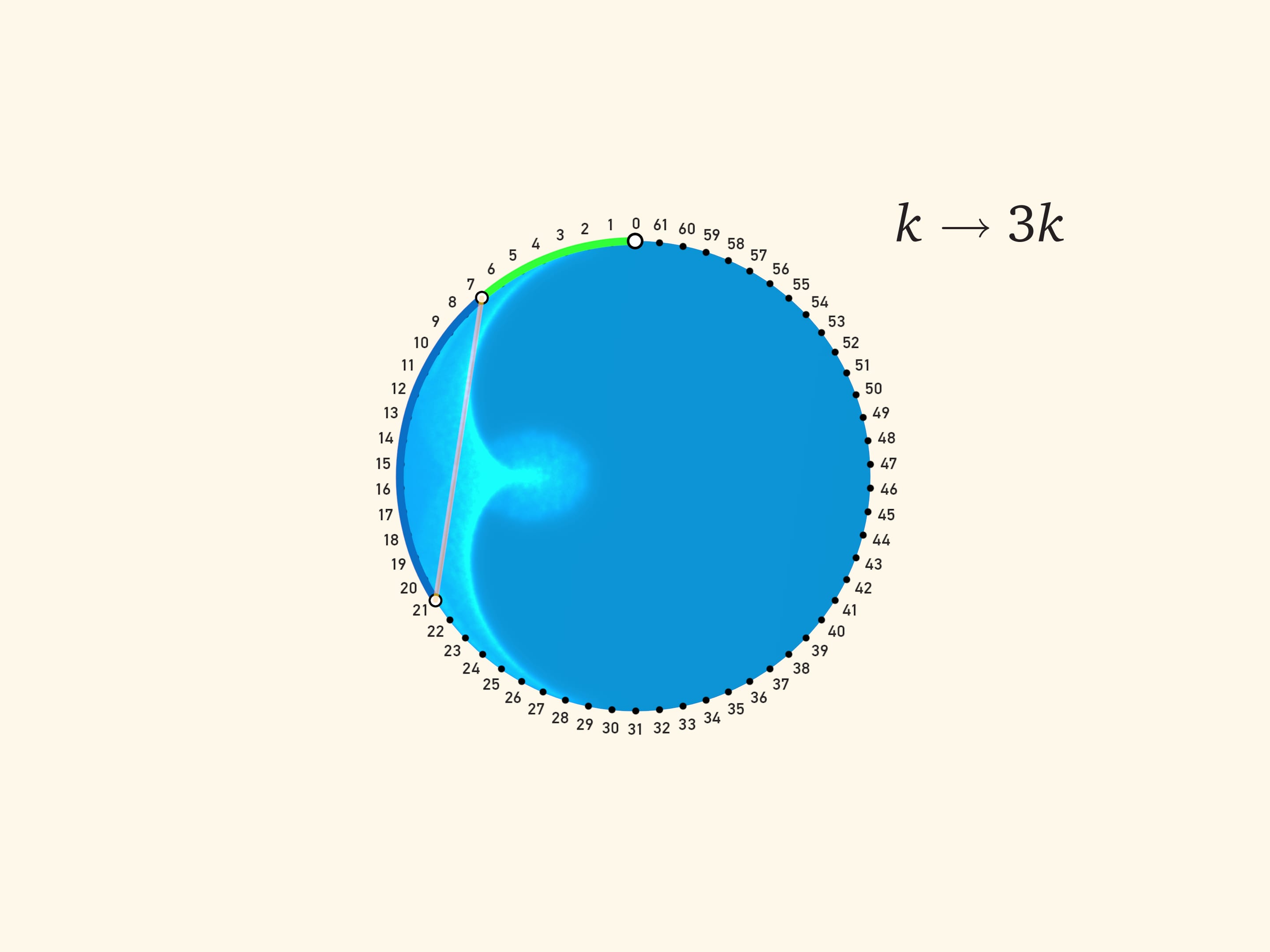
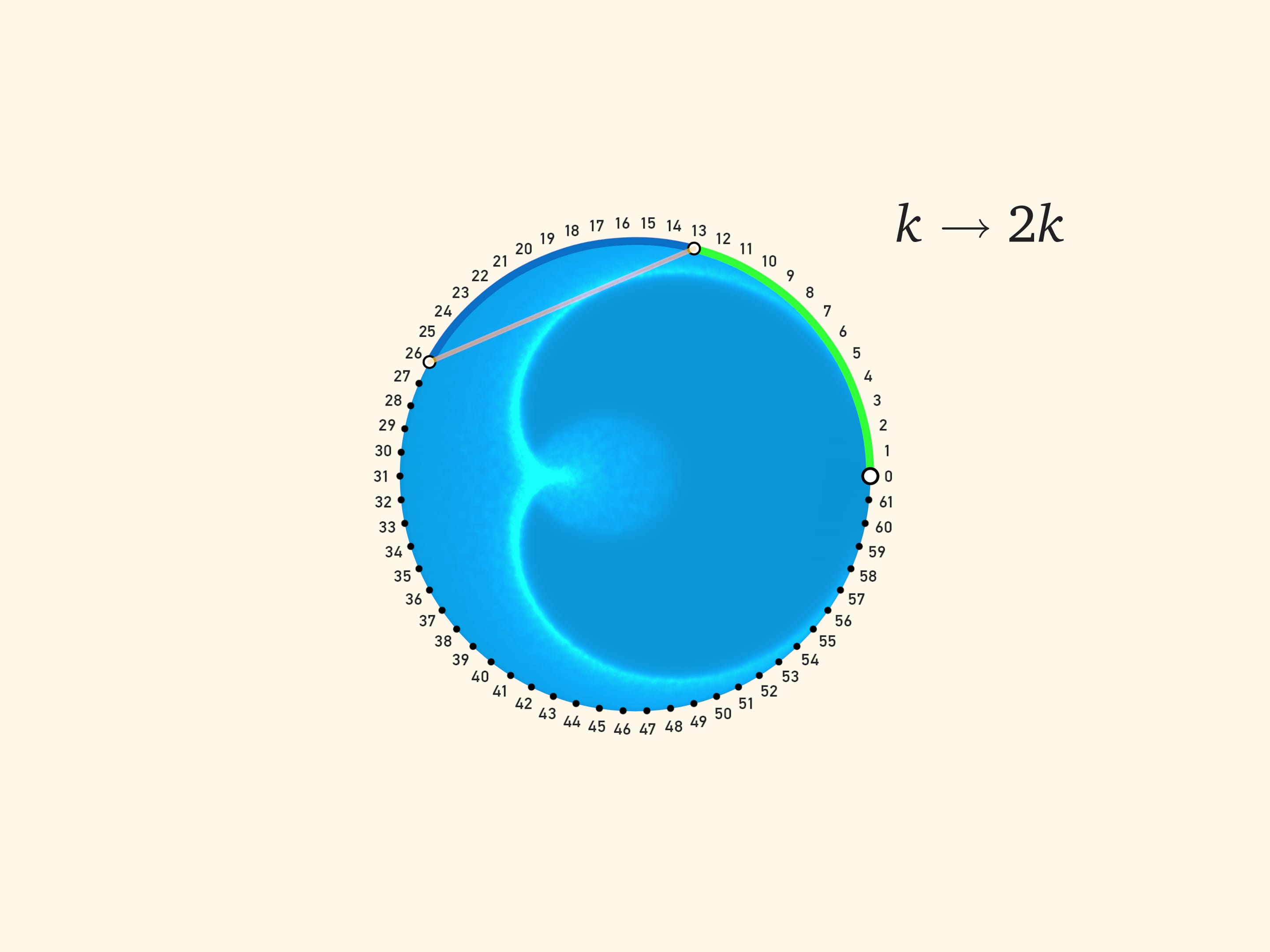
Две зелёные дуги в сумме равны синей, а значит, синяя дуга в два раза больше салатовой. Считая от неподвижного конца салатовой дуги (верхней точки круга), получаем правило подсвеченной хорды: от точки с углом $\alpha$ к точке с углом $3\alpha$. В дискретном виде этот закон уже знаком нам по сюжету Кардиоида и нефроида: на окружности равномерно расставляются $N$ точек и для каждого $k$ проводится отрезок, соединяющий точку с номером $k$ с точкой с номером $3k$. (Так как «живём» на окружности, то эту операцию надо делать «по модулю $N$»: если число оказалось больше $N$, то делим его на $N$ с остатком и рассматриваем этот остаток.)
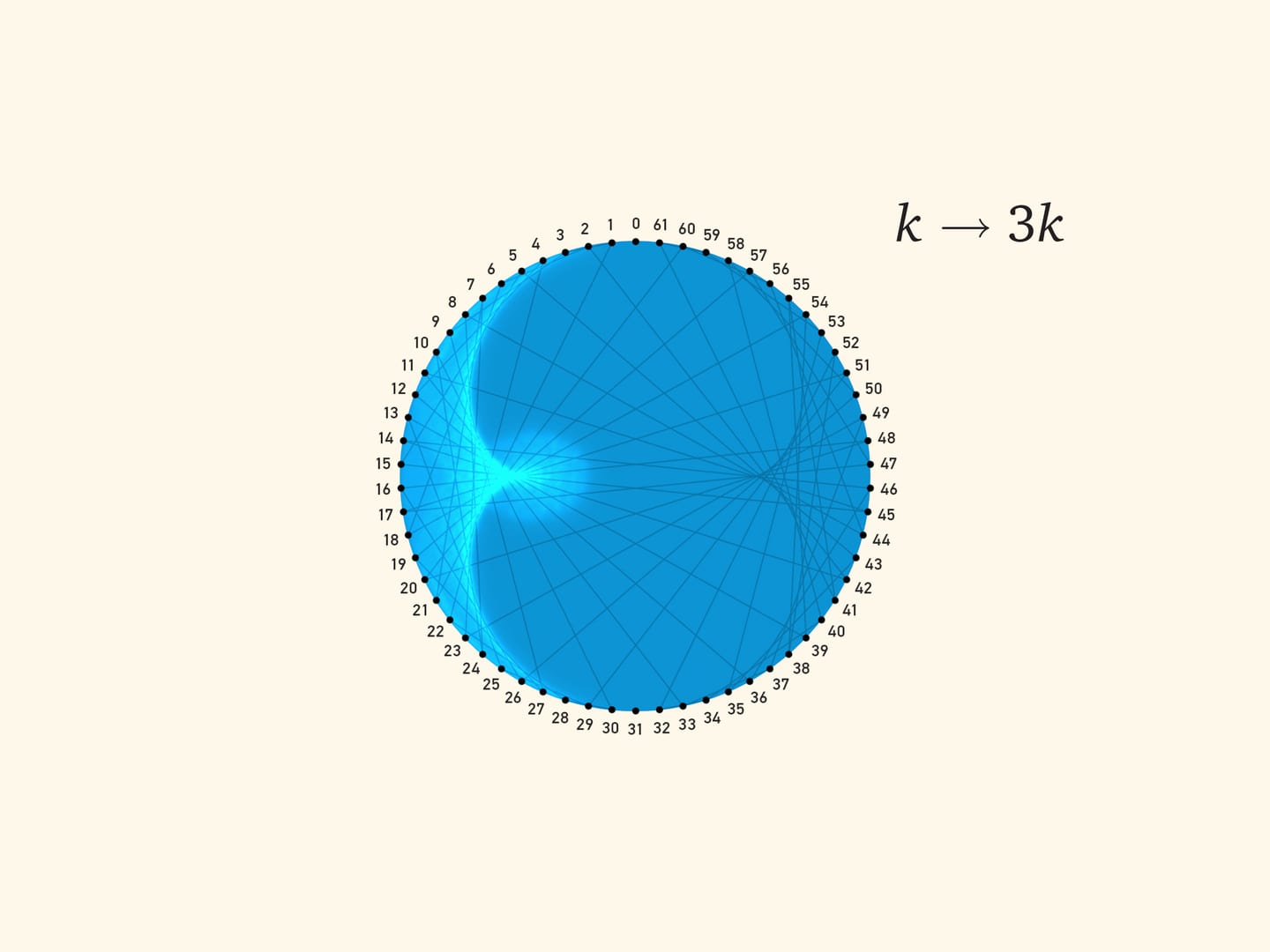
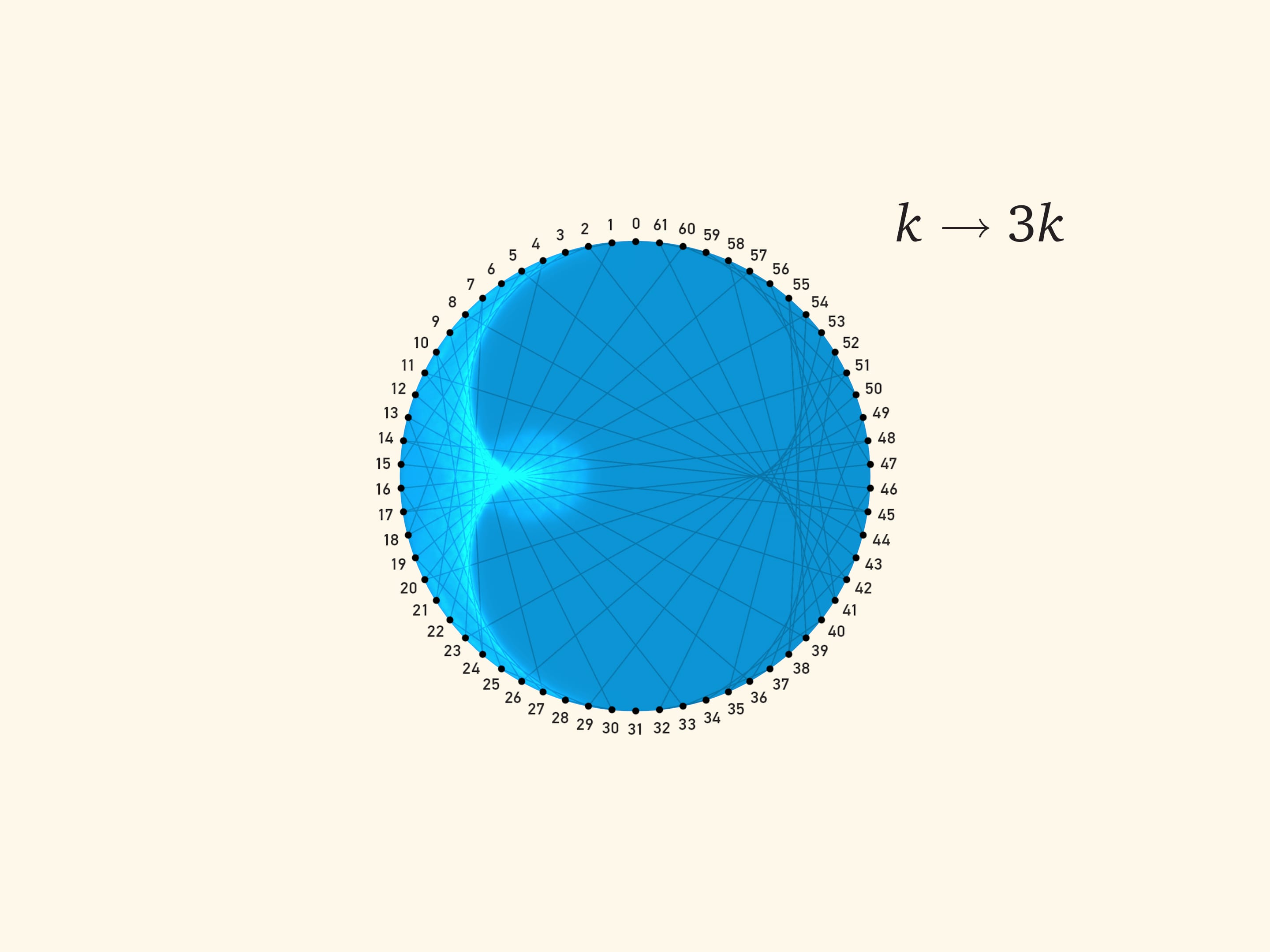
Доказательство того, что при проведении хорд по этому правилу получается именно нефроида, опирается на теорему о двух кругах. А сейчас предлагаем вам распечатать на бумаге картинку с хордами, положить вырезанный круг внутрь цилиндрической посуды, посветить фонариком и убедиться, что образующаяся каустика является огибающей семейства хорд $k\to 3k$.
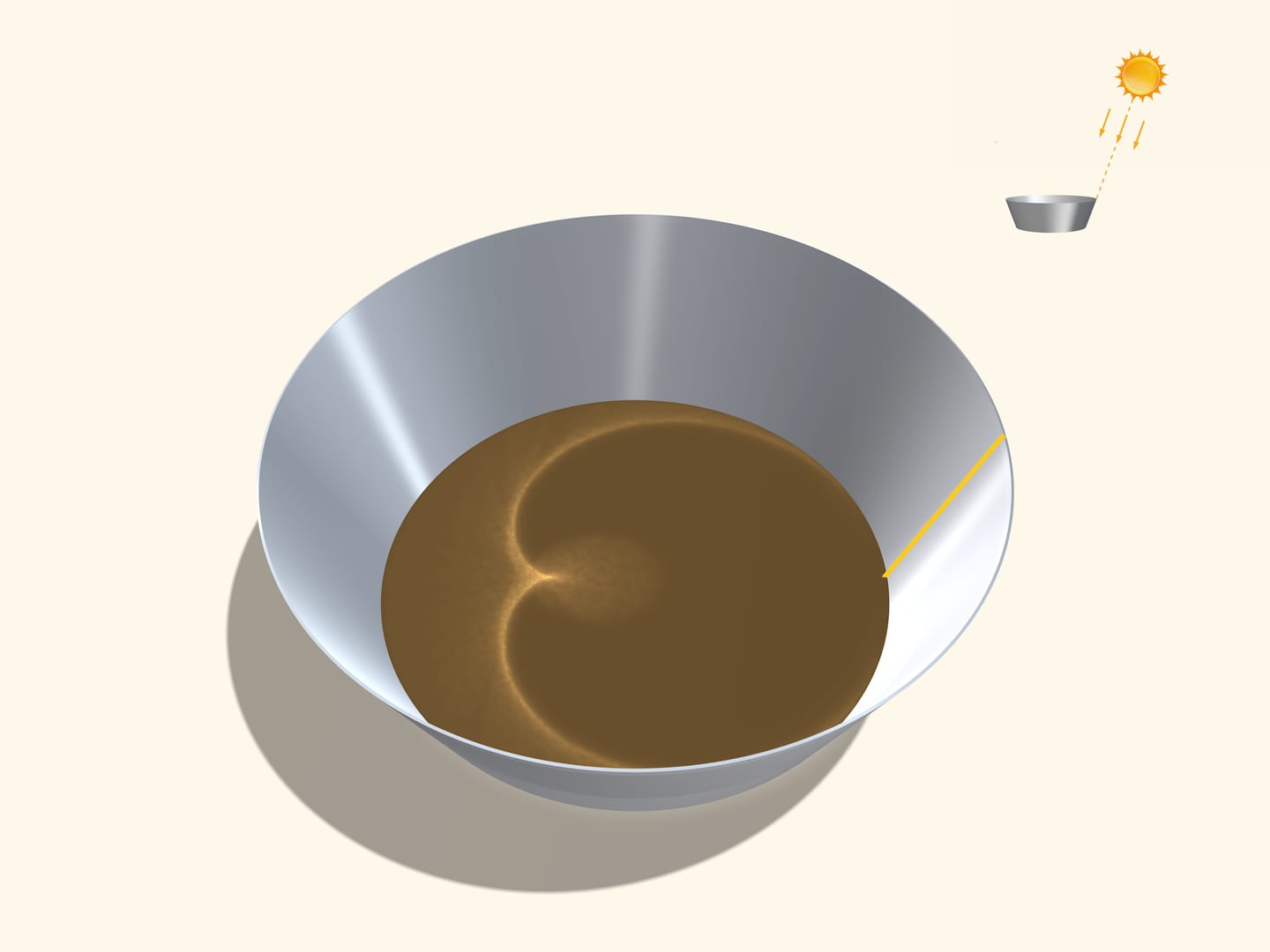
Перейдём к конусу (прямому круговому). Конус с отражающей внутренней поверхностью в современном быту встречается реже (а раньше жестяные вёдра всегда были коническими), но конические чашки — не редкость. Когда солнечный свет падает в такую чашку, то на дне можно увидеть различные кривые. Выделяющийся интересный случай — когда лучи Солнца параллельны образующей конуса. При этом условии каустика будет иметь форму кардиоиды.
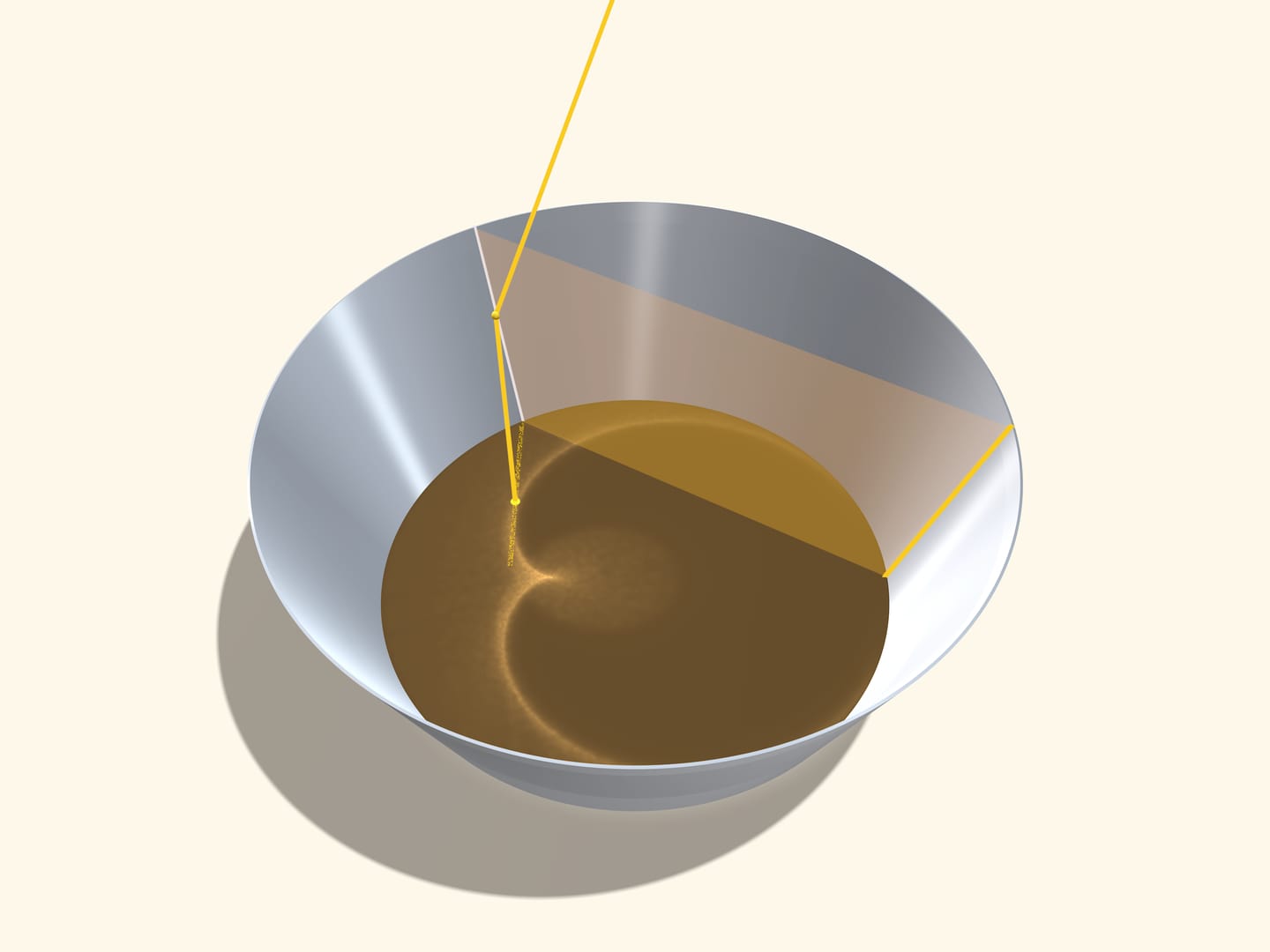
По сути рассмотрение конуса такое же, как и цилиндра, но теперь есть выделенная образующая — «направленная на Солнце», параллельно которой приходят лучи света. Закон отражения одного луча всё тот же, и определяется вектором нормали к касательной плоскости в точке отражения. Все лучи, отражающиеся от одной образующей, на поверхности кофе дают точки, объединяющиеся в отрезок хорды. Солнечный свет расслаивается на «веер» плоскостей, каждая из которых проходит через «солнечную» образующую и ещё какую-то образующую конуса. Плоскость лучей, отражённых от одной образующей, будет симметрична «своей» плоскости расслоения относительно осевого сечения (плоскости, содержащей образующую и ось конуса). Другими словами, плоскость расслоения и плоскость отражённых лучей — грани двугранного угла, ребром которого является образующая конуса, а биссекторная плоскость этого двугранного угла содержит ось конуса.
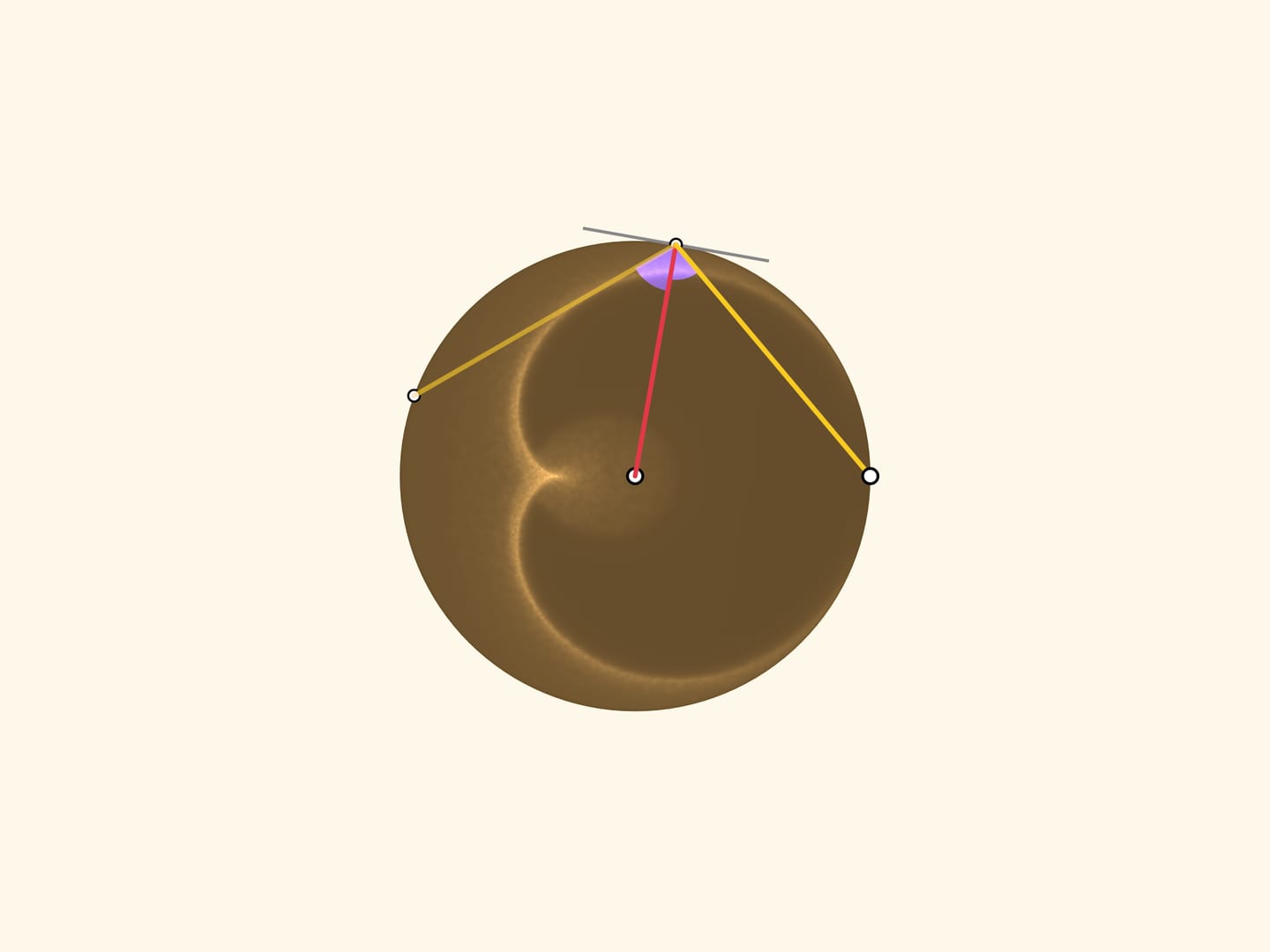
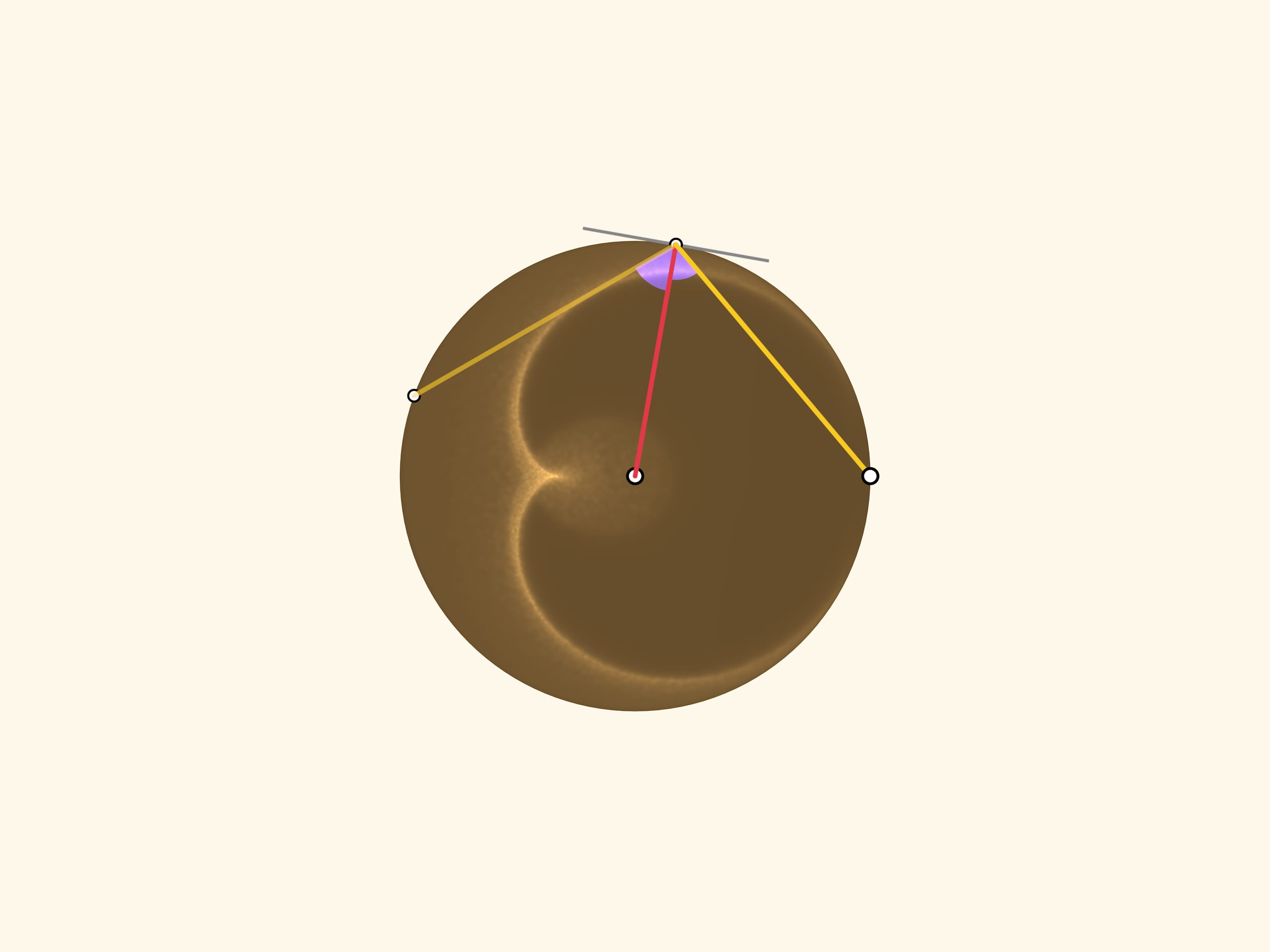
На виде «сверху» точка, соответствующая солнечной образующей, будет неподвижна, а луч, вышедший из неё, уйдёт после отражения под тем же углом относительно радиуса (так как в конусе плоскости пришедшего и отражённого лучей были симметричны относительно осевого сечения).
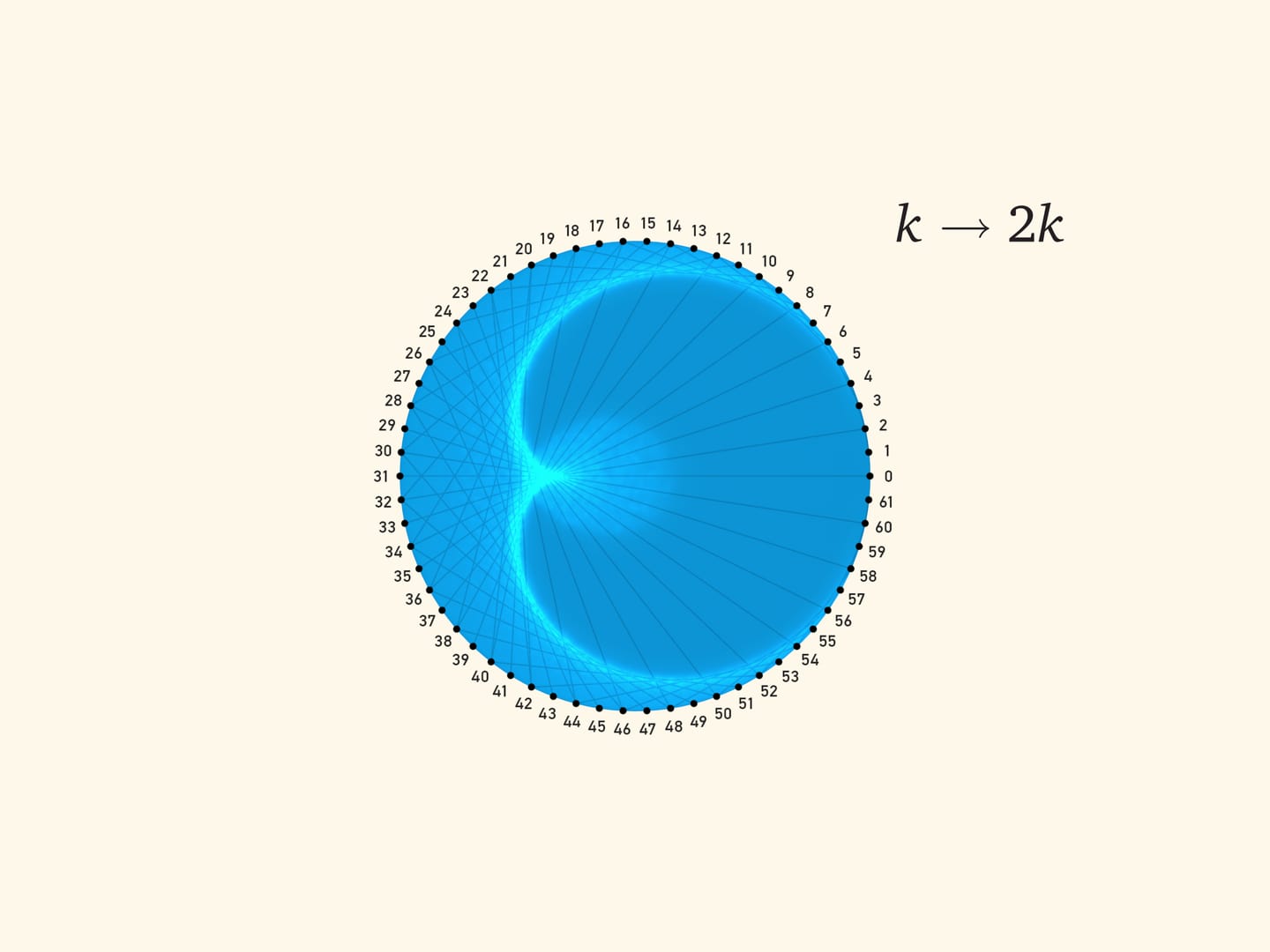
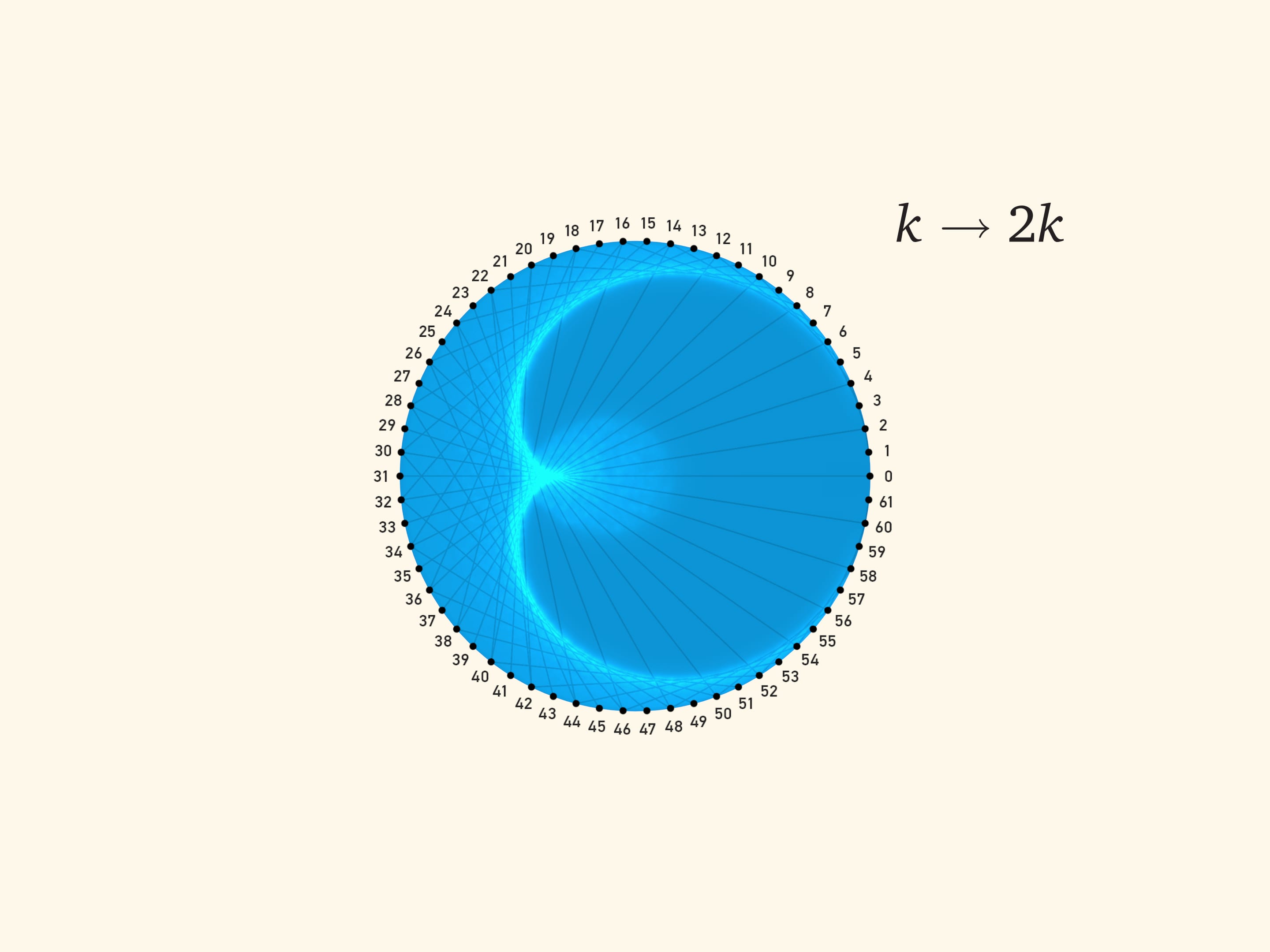
Зелёная и синяя дуги равны, а значит, хорды, являющиеся касательными к каустике и образовывающие её как огибающую, отвечают правилу: от точки с углом $\alpha$ к точке с углом $2\alpha$, где угол считается от солнечной образующей.
Итак, в конусе, когда солнечные лучи параллельны одной из его образующих, возникает кардиоида — эпициклоида с одним остриём напротив солнечной образующей.
Эксперименты лучше проводить на свежем воздухе — и для здоровья полезнее, и можно считать, что лучи от Солнца параллельны друг другу. Именно этот случай — когда лучи параллельны друг другу — и показан в сюжете. Но хорошее приближение к описанным каустикам можно увидеть и в домашних условиях, используя, например, фонарик телефона.
Существует и другой механизм образования каустик. На праздничном столе при ярком освещении можно увидеть каустики, образованные светом, прошедшим через хрустальные/стеклянные бокалы. Здесь основную роль играет не отражение, а преломление света на границе сред. Сейчас даже делают такие стеклянные пластины, которые собирают свет в каустику заданной формы — светом вырисовывается портрет или какая-нибудь надпись. Но это уже тема для другого сюжета.
Другие этюды раздела «Геометрическая оптика»
