Если вам приходилось собирать дома шкаф, то вы прекрасно помните, что пока не прибита задняя стенка, он изгибается. Как только задняя стенка поставлена на место, шкаф — незамкнутый многогранник с краем — становится жёстким. Если к нему добавить переднюю стенку или сделать на крае любую другую надстройку, замыкающую многогранник, то жёсткость, конечно, останется.
Бывают ли замкнутые изгибаемые многогранники?
Ответ на этот вопрос долго не могли найти. Как обычно в науке, при исследовании задачи следует рассмотреть более простой случай. В случае задачи об изгибаемых многогранниках — рассмотреть задачу не в пространстве, а на плоскости, где аналогом многогранника является многоугольник.
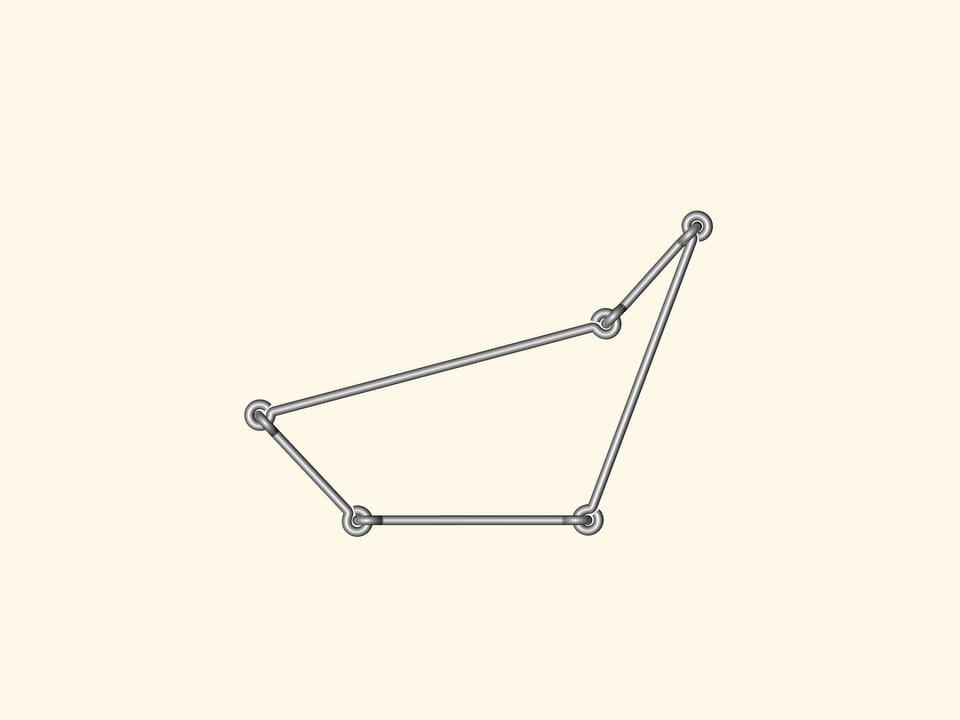
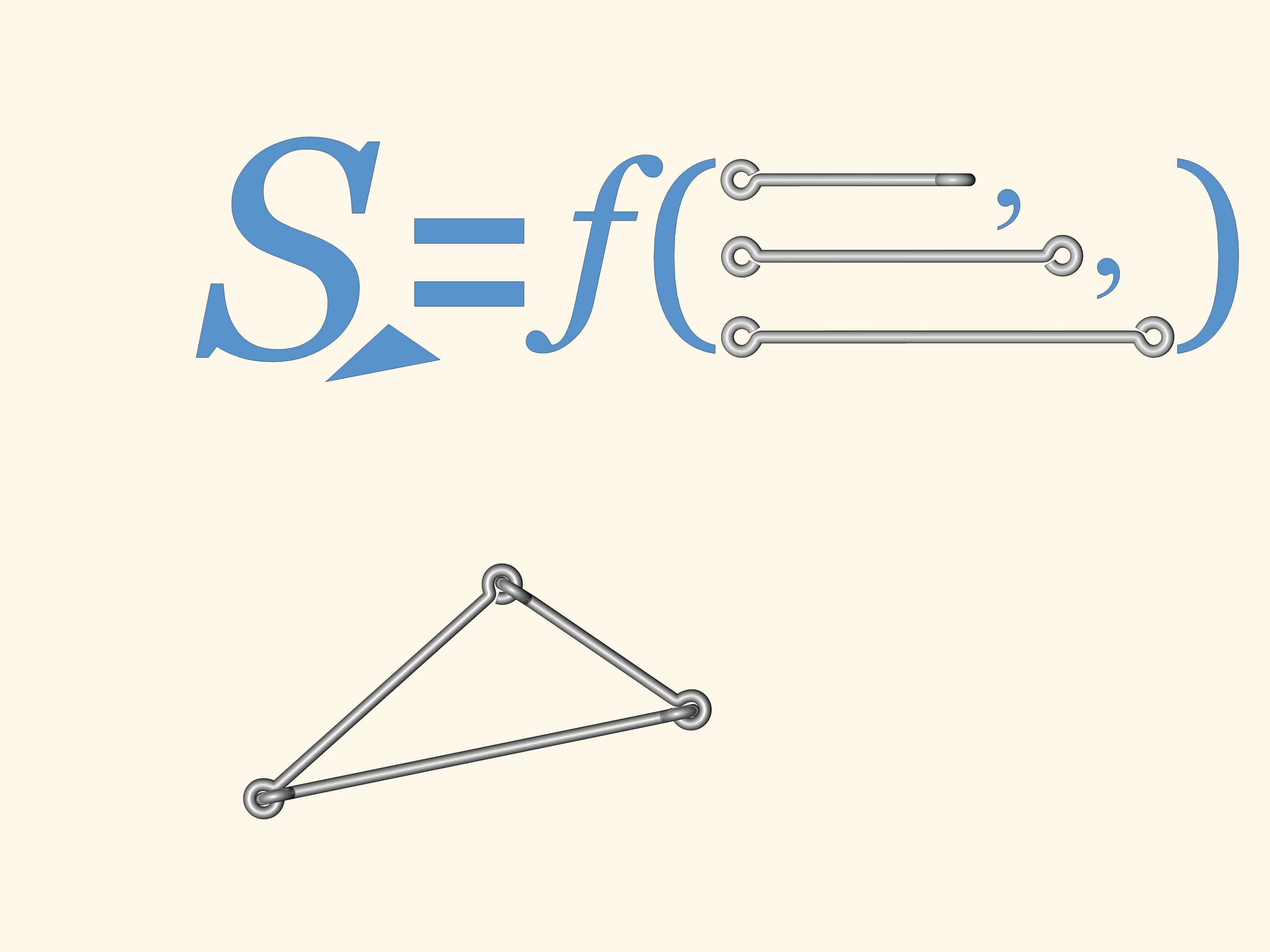
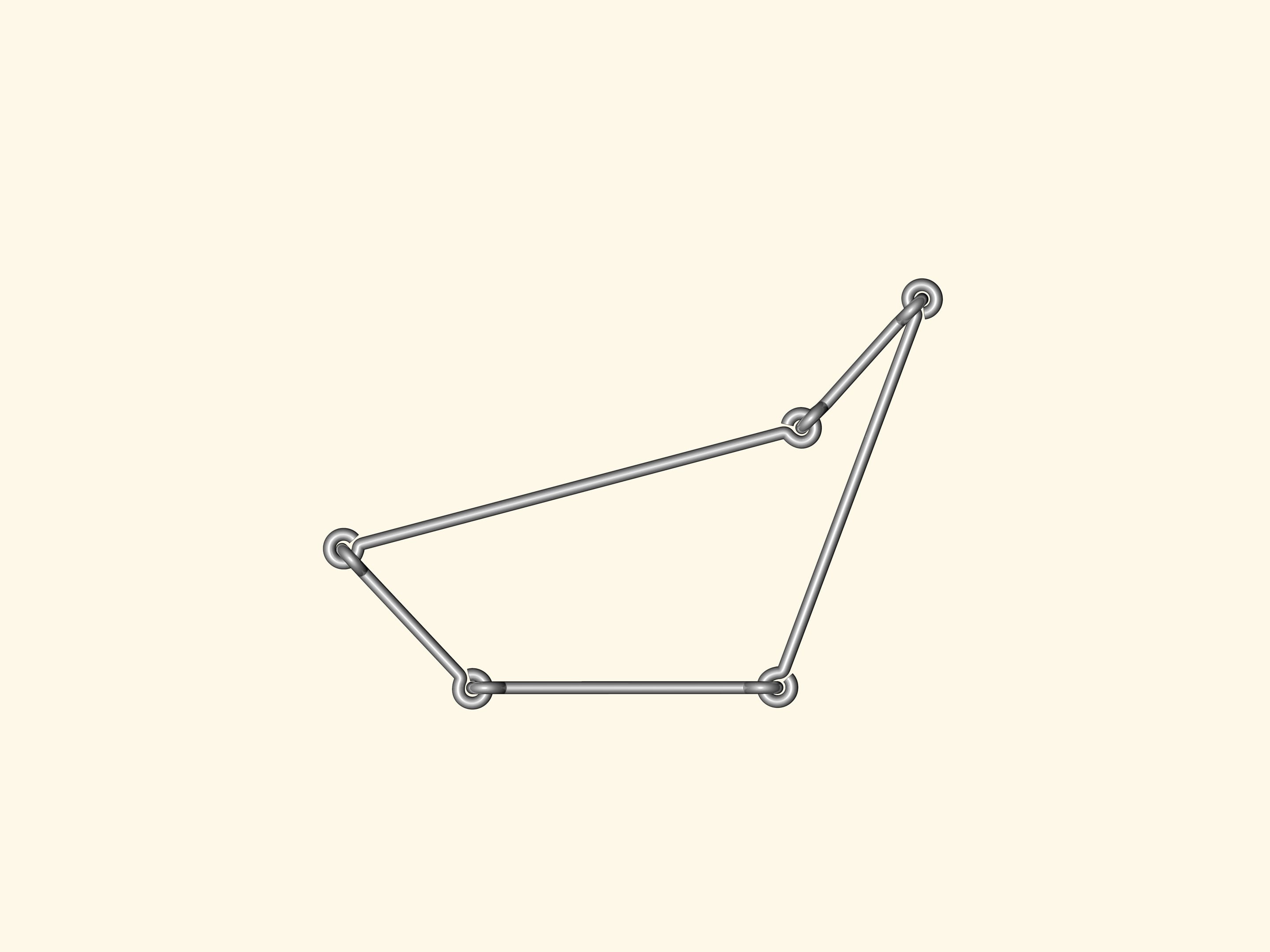
Бывают ли изгибаемые многоугольники? Т. е. такие, у которых стороны фиксированы, в углах возможно изгибание (в плоскости), а сами многоугольники меняют форму? Такую модель каждый может изготовить из проволоки, используя стандартное соединение в углах.
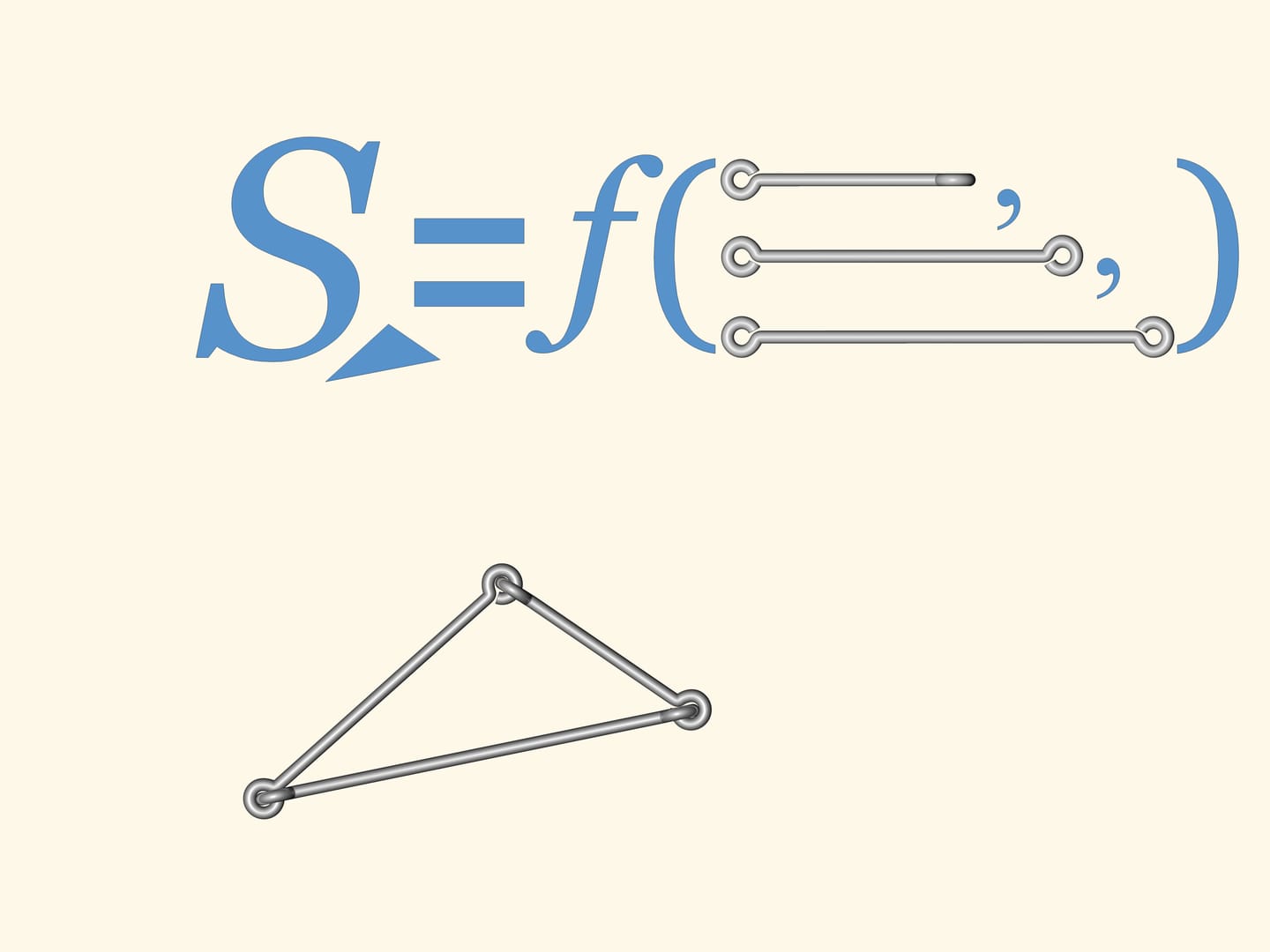
Если таким способом сделать треугольник, то он не будет изгибаться. Т. е. длины сторон полностью определяют треугольник. А значит, определяют и его площадь — формула Герона позволяет вычислять её, исходя только из длин сторон.
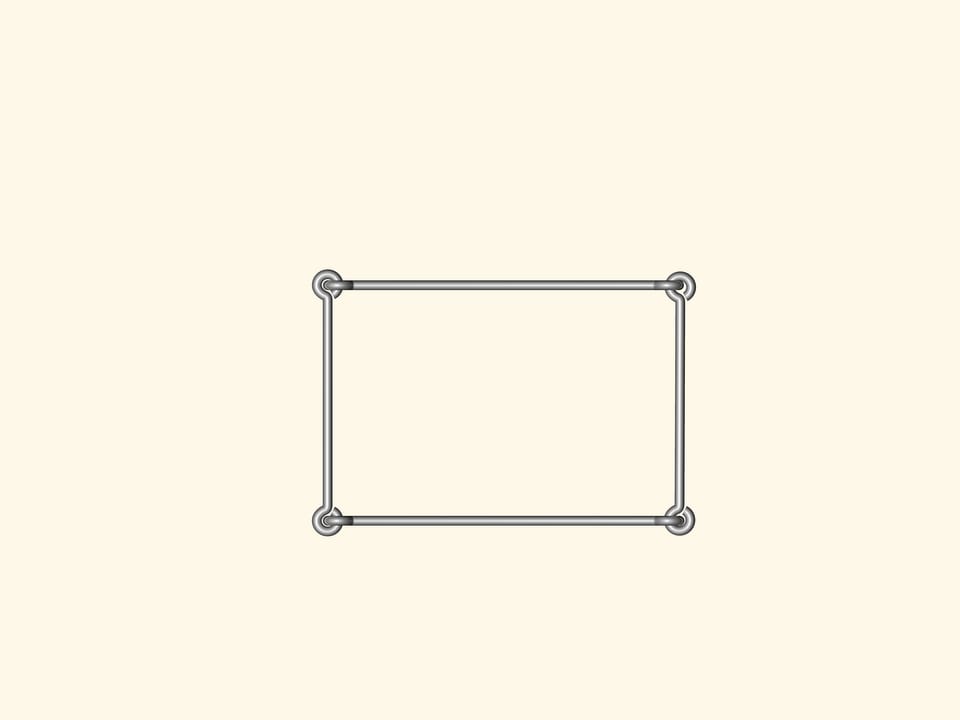
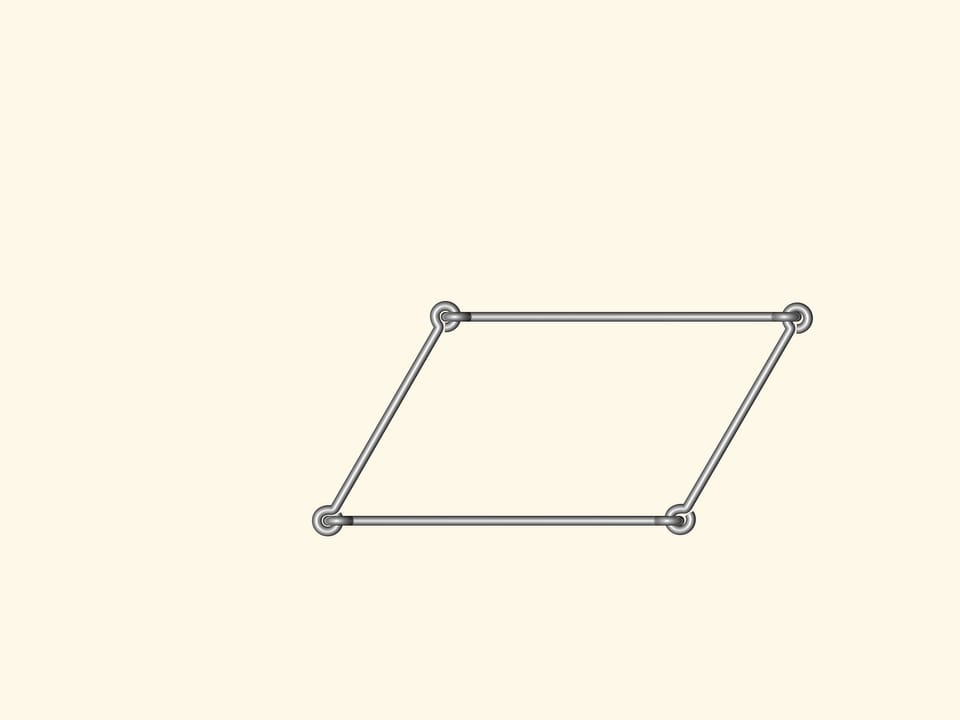
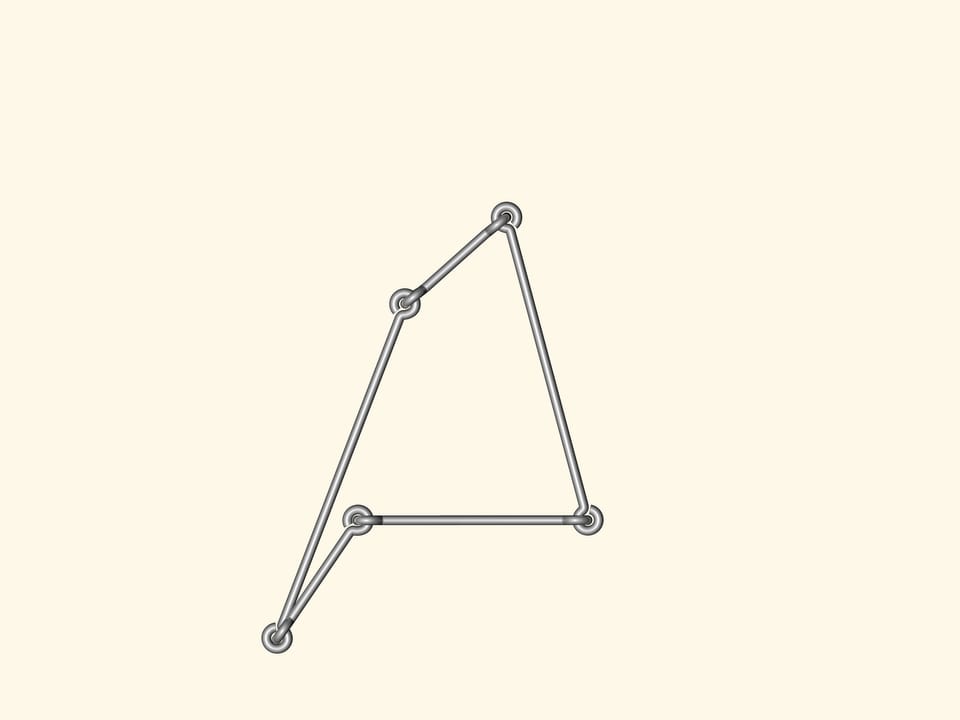
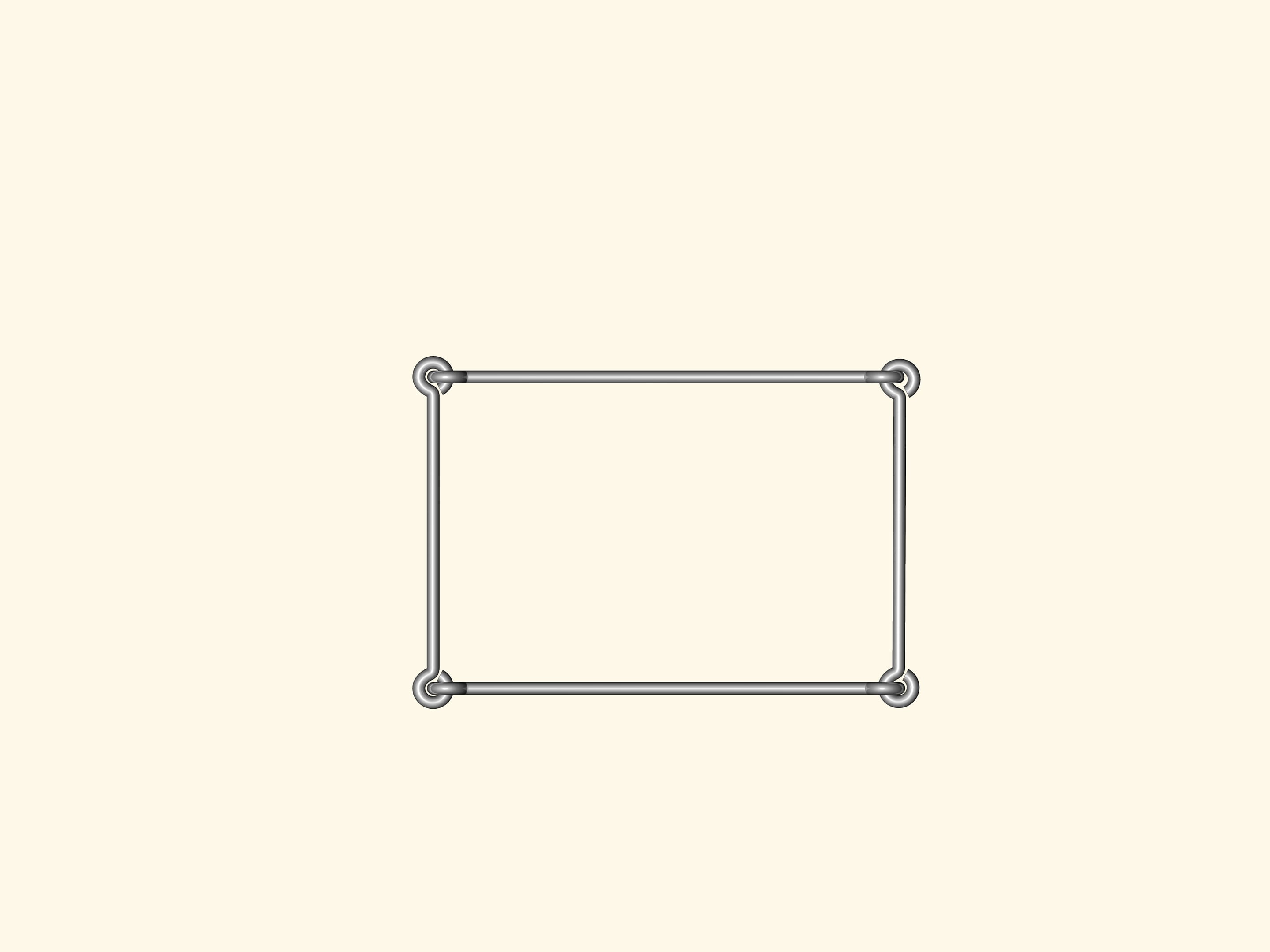
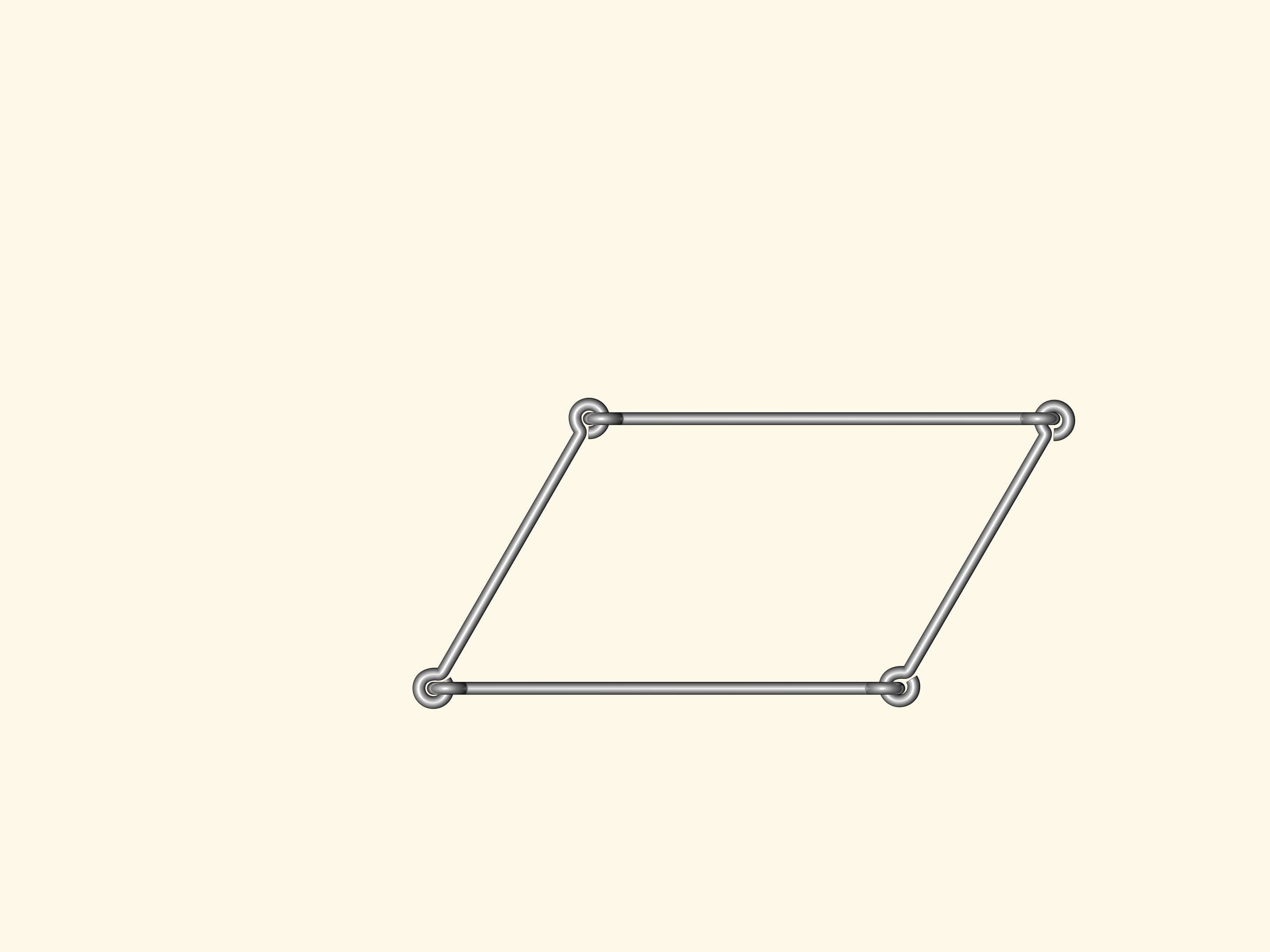
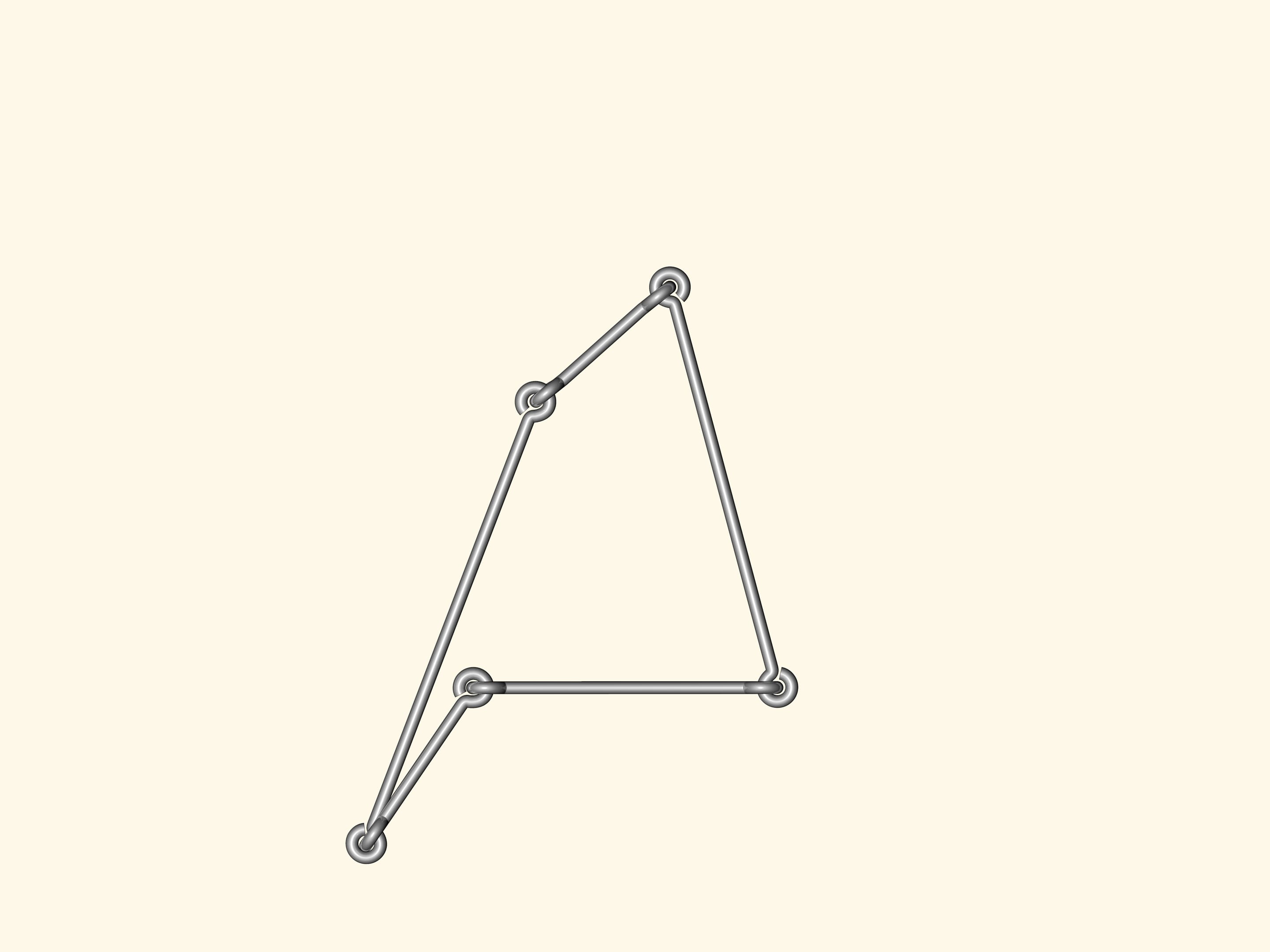
Если же сделать проволочный четырёх- или пятиугольник, или же многоугольник с бóльшим количеством вершин, то любой из них будет изгибаться. Как следствие, аналога формулы Герона — формулы для вычисления площади многоугольника, исходя только из длин сторон — при количестве углов большем трёх, быть не может.
Вернёмся в пространство. Что же такое изгибаемый многогранник, если он существует? По аналогии с плоской задачей, грани (имеющие размерность на единицу меньше размерности пространства) должны быть жёсткими пластинами. А двугранный угол, соединяющий любые две грани, должен иметь возможность меняться, как будто ребро («грань», имеющая размерность один) реализовано с помощью рояльной петли.
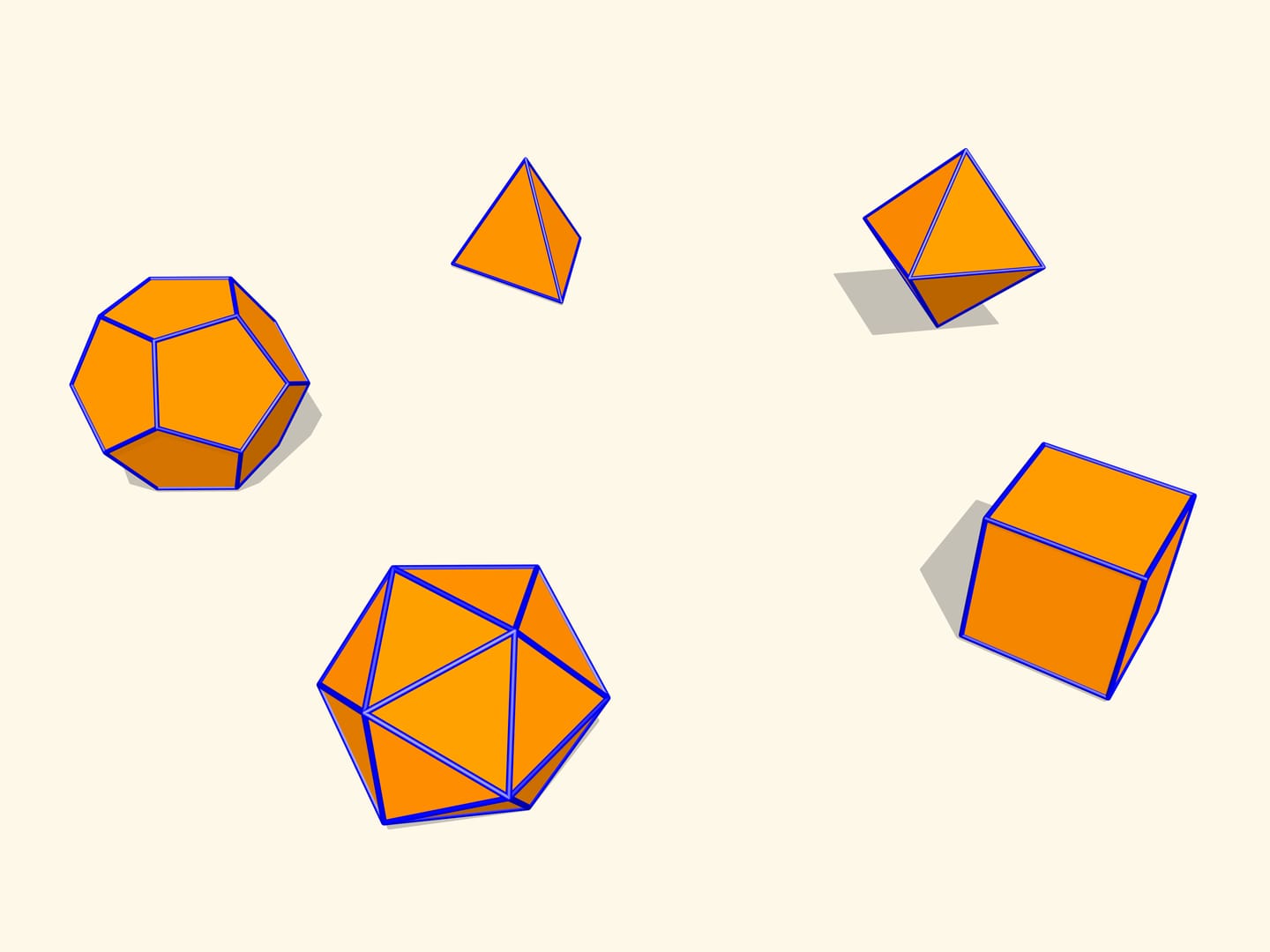
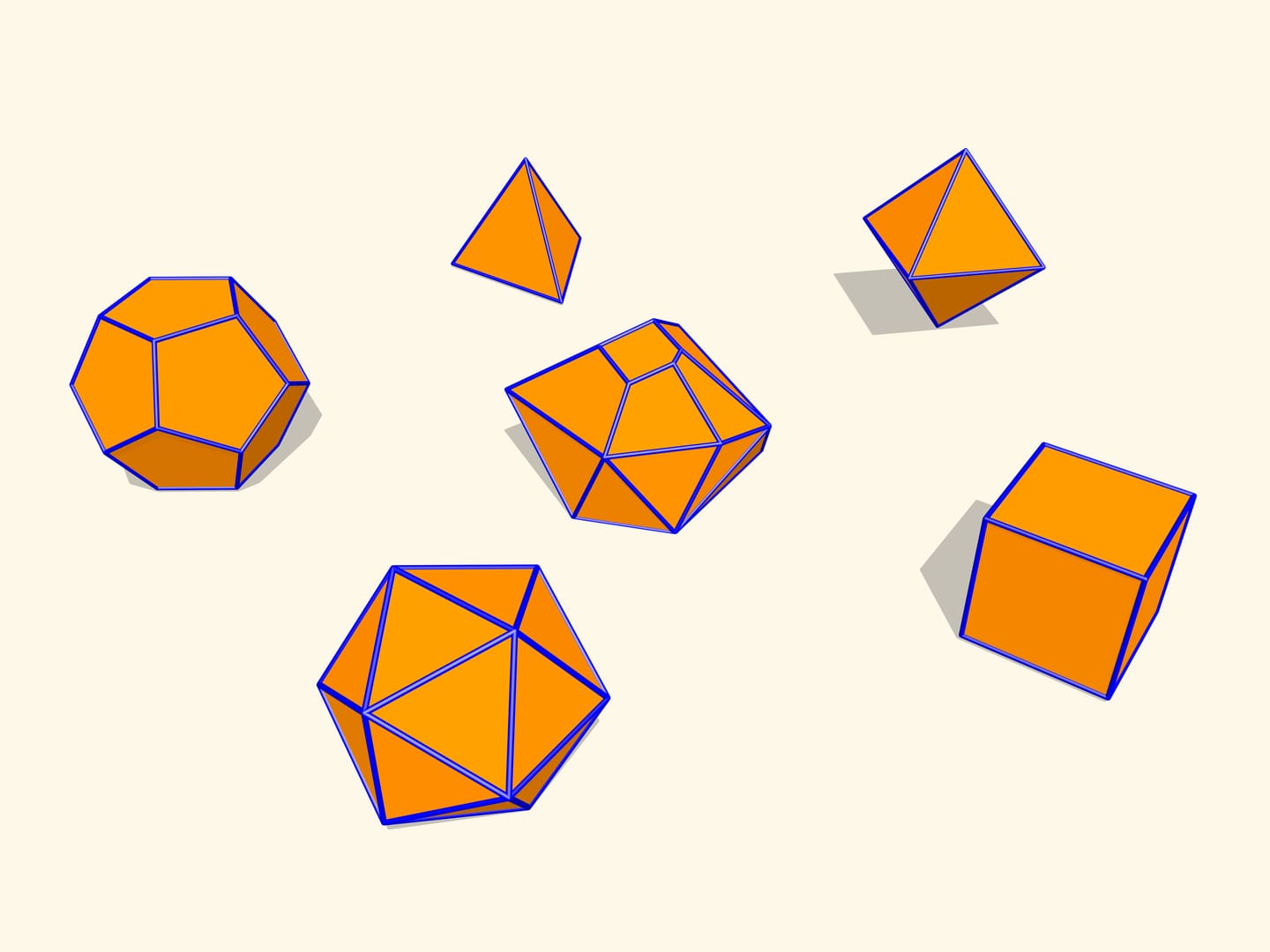
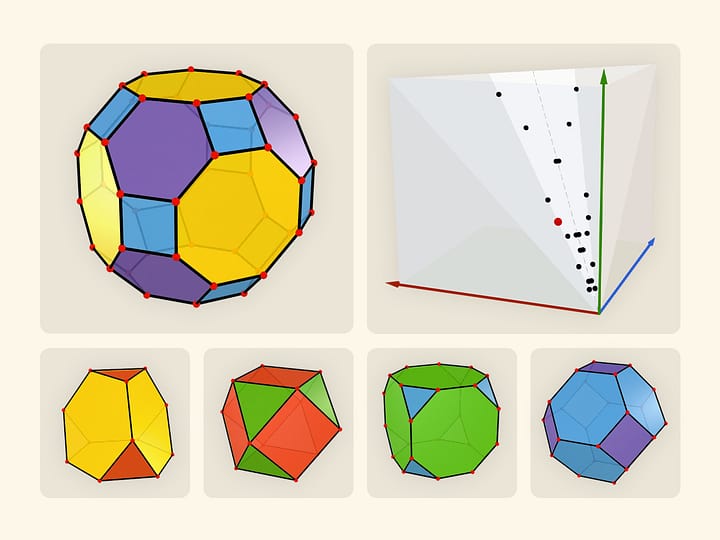
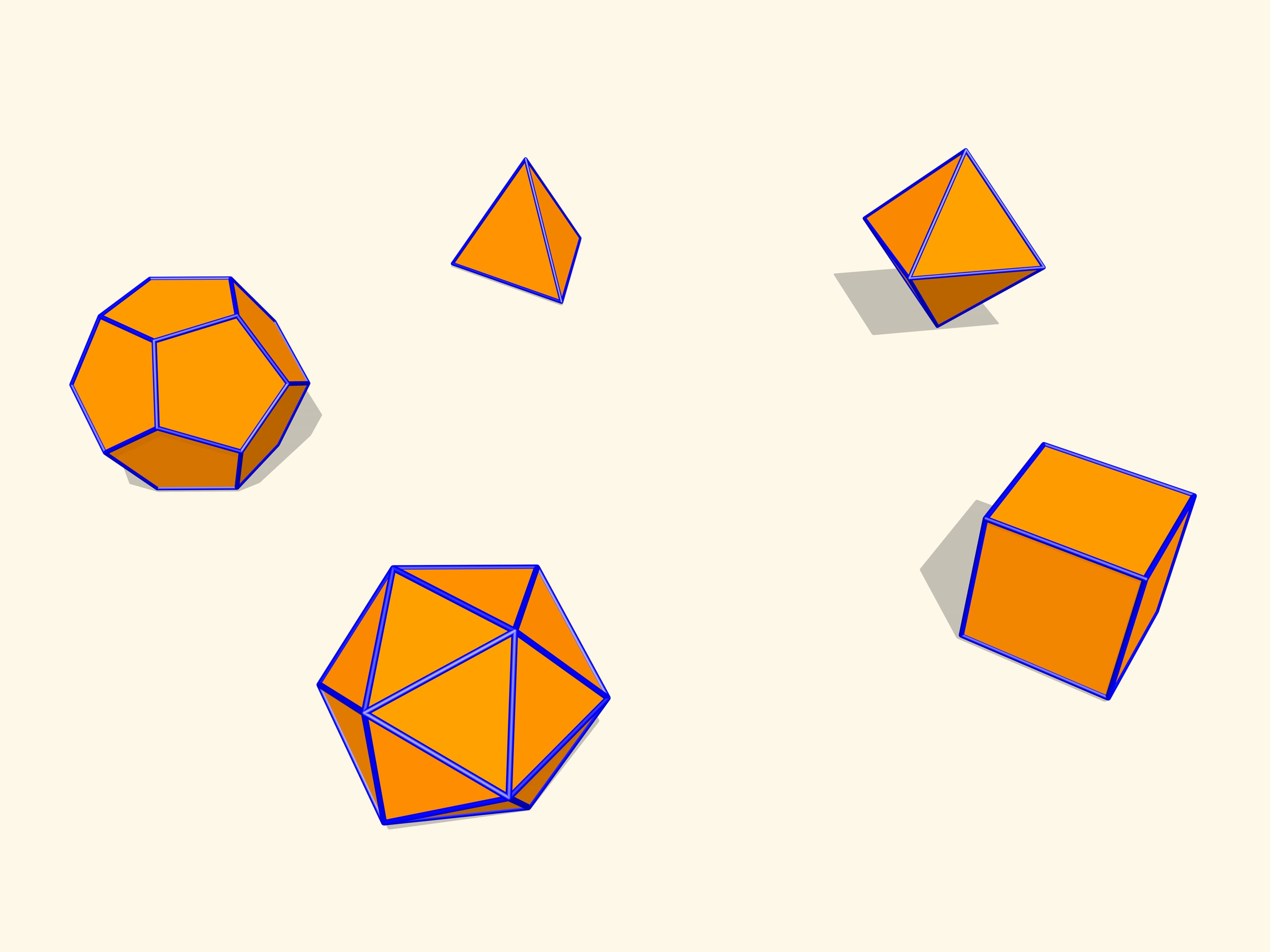
Давайте рассмотрим правильные многогранники. Если сделать их модели «на рояльных петлях» в качестве ребер, то можно убедиться, что изгибаться они не будут. Оказывается, это общий факт для выпуклых многогранников. Теорема, доказанная французским математиком Огюстеном Луи Коши (1789—1857) в 1813 году, говорит о том, что выпуклый многогранник с данным набором граней и условиями их склейки единственен. Т. е. выпуклый многогранник изгибаемым не бывает.
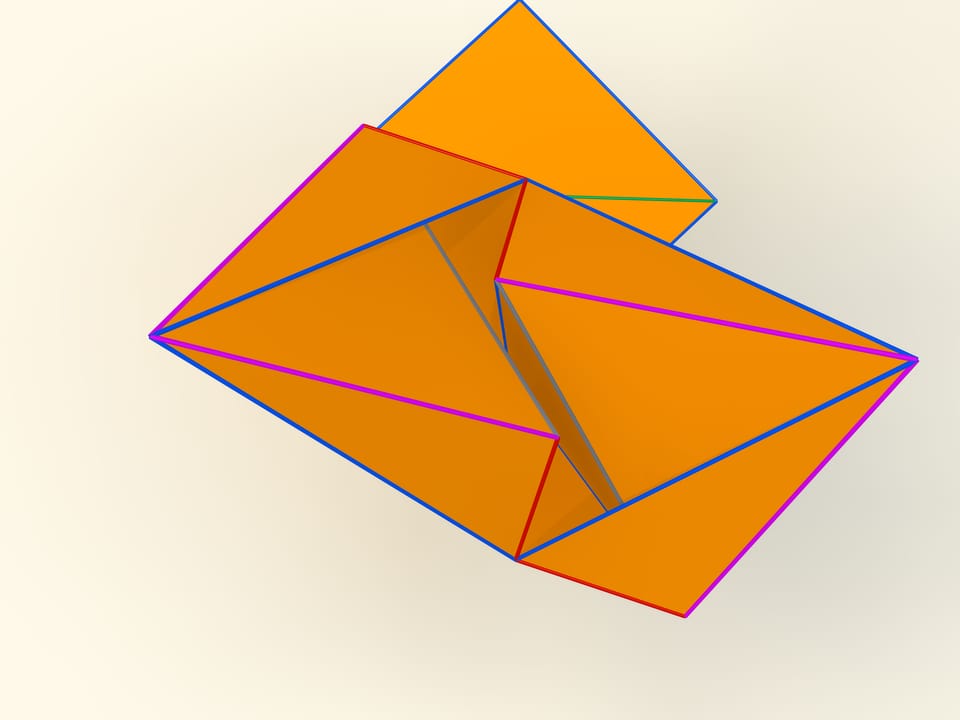
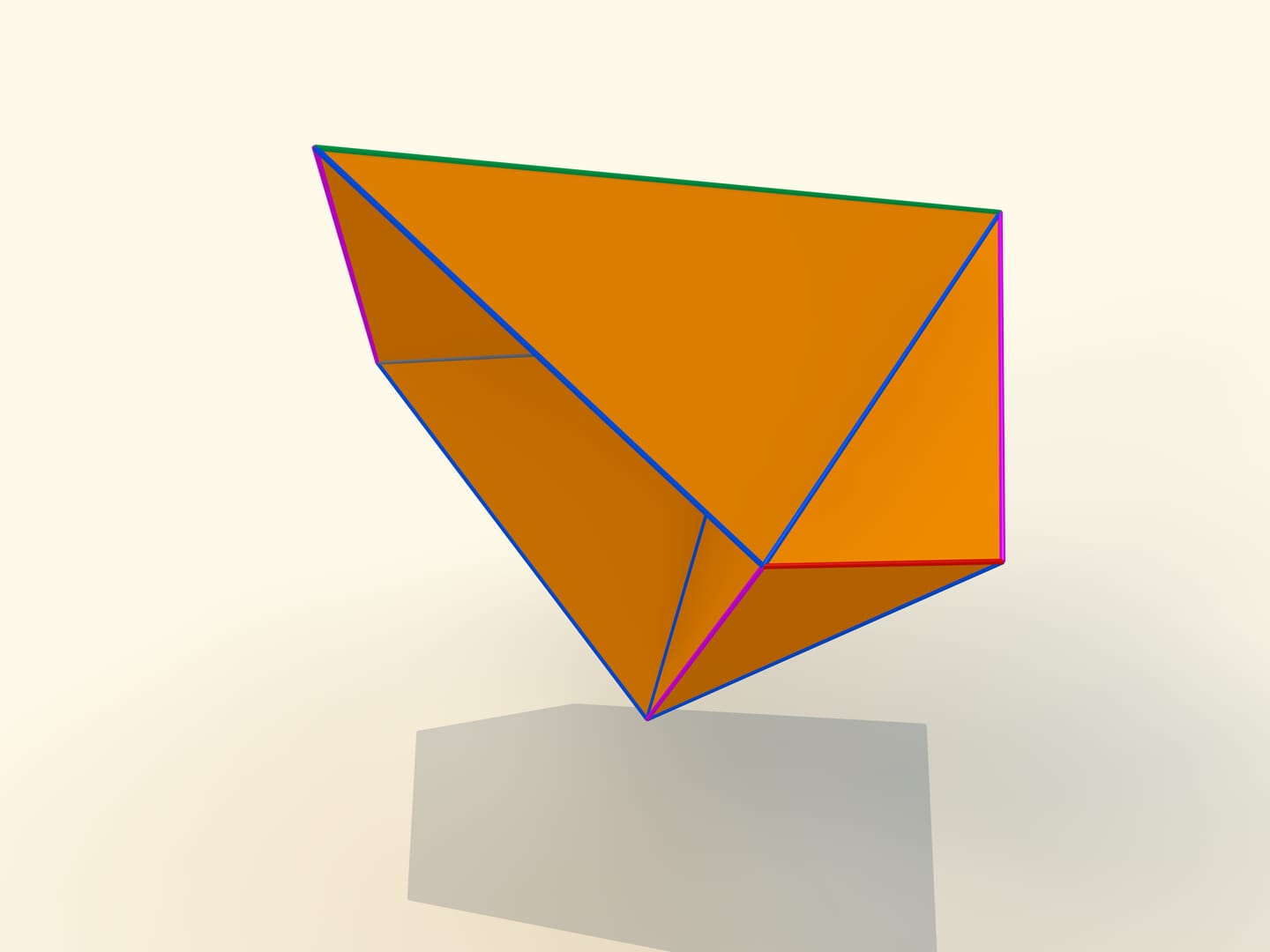
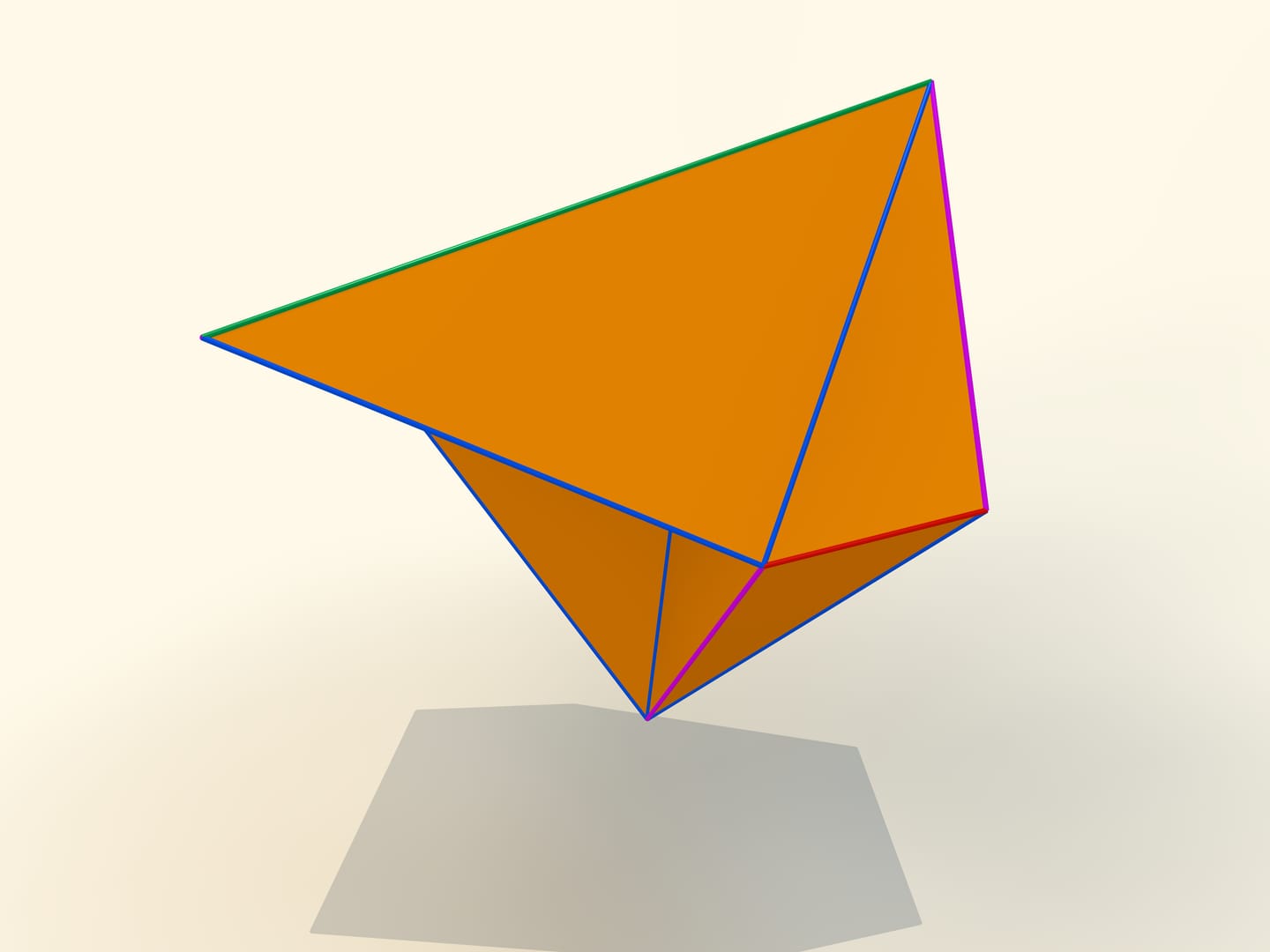
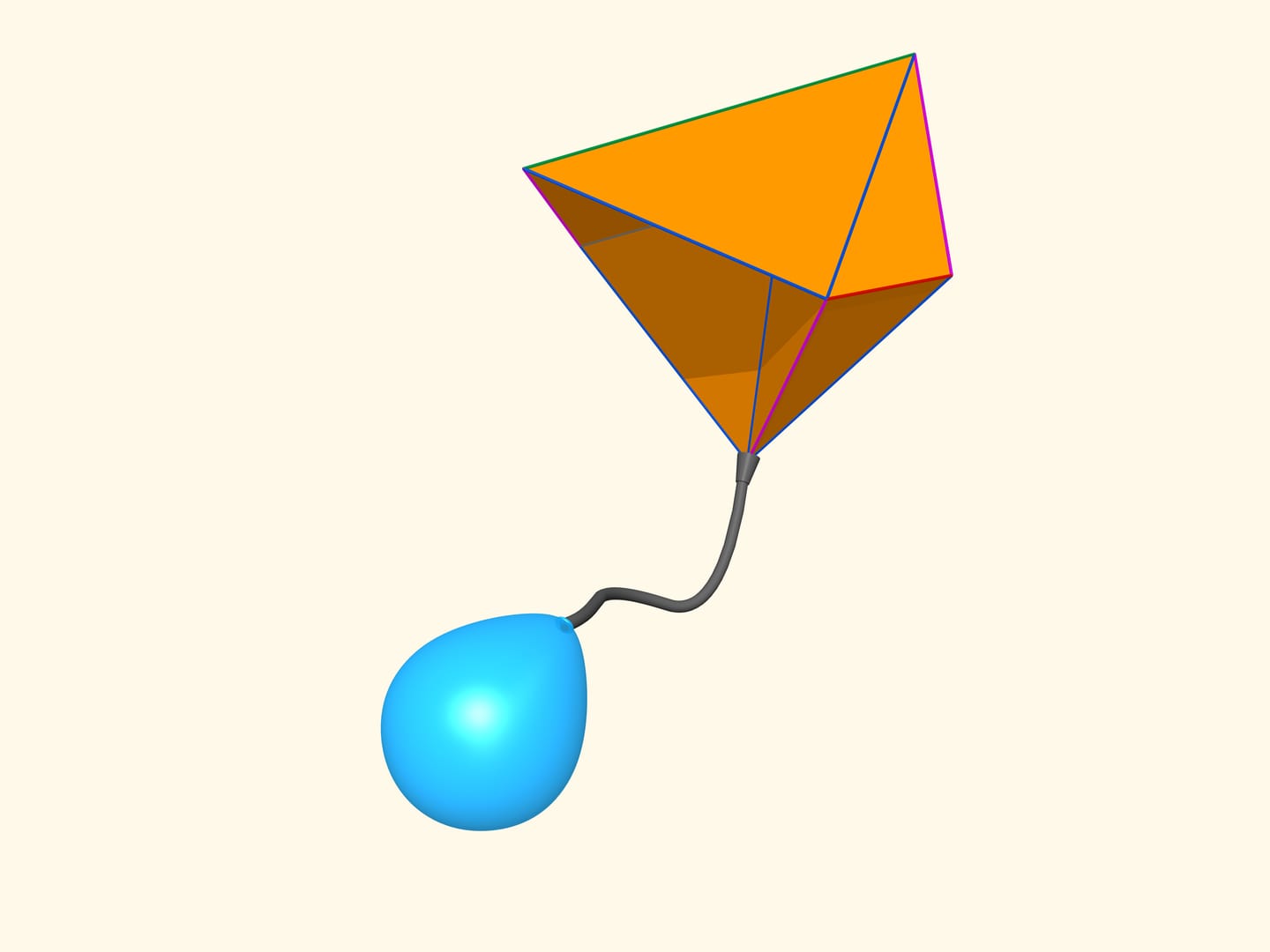
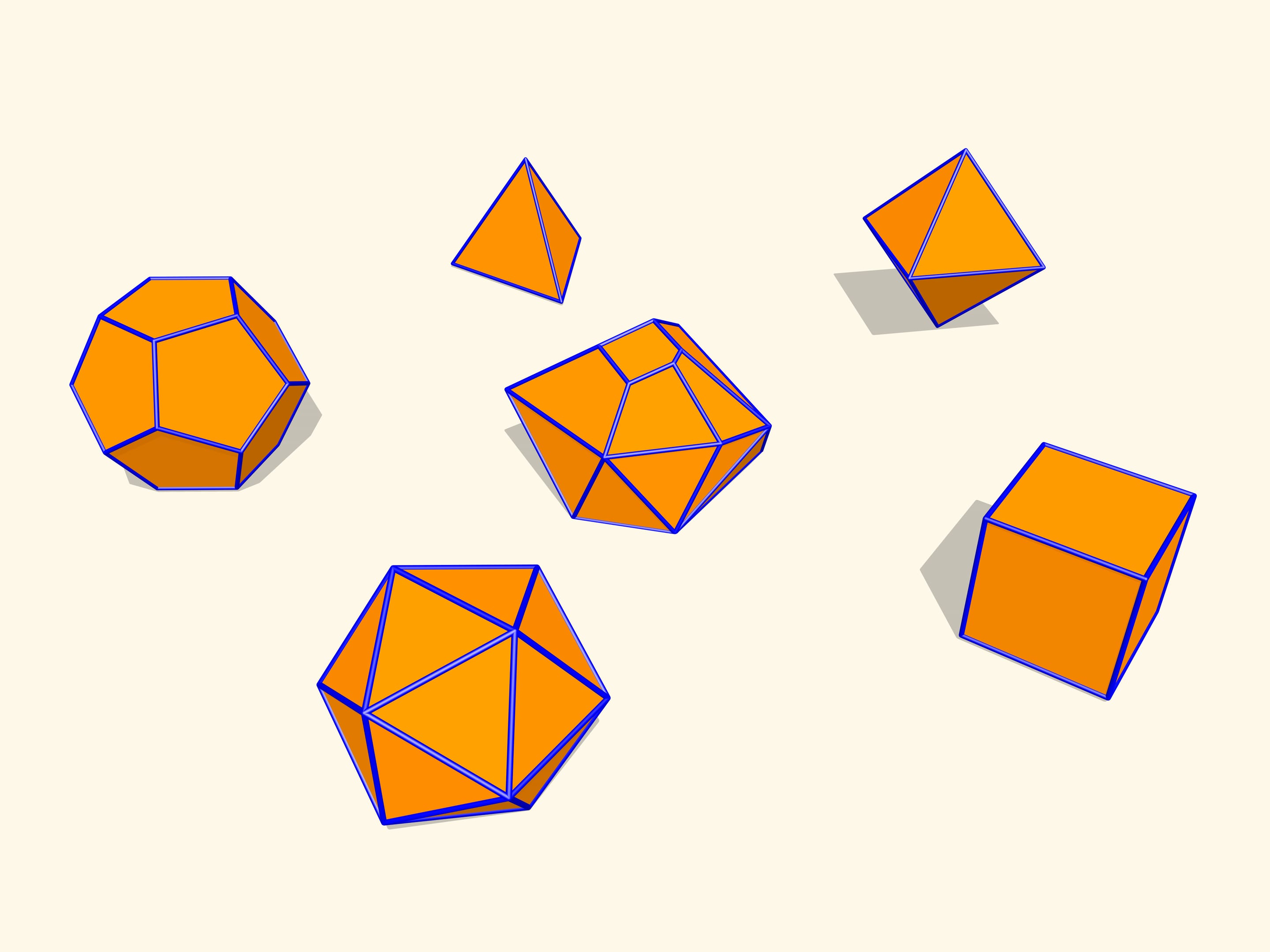
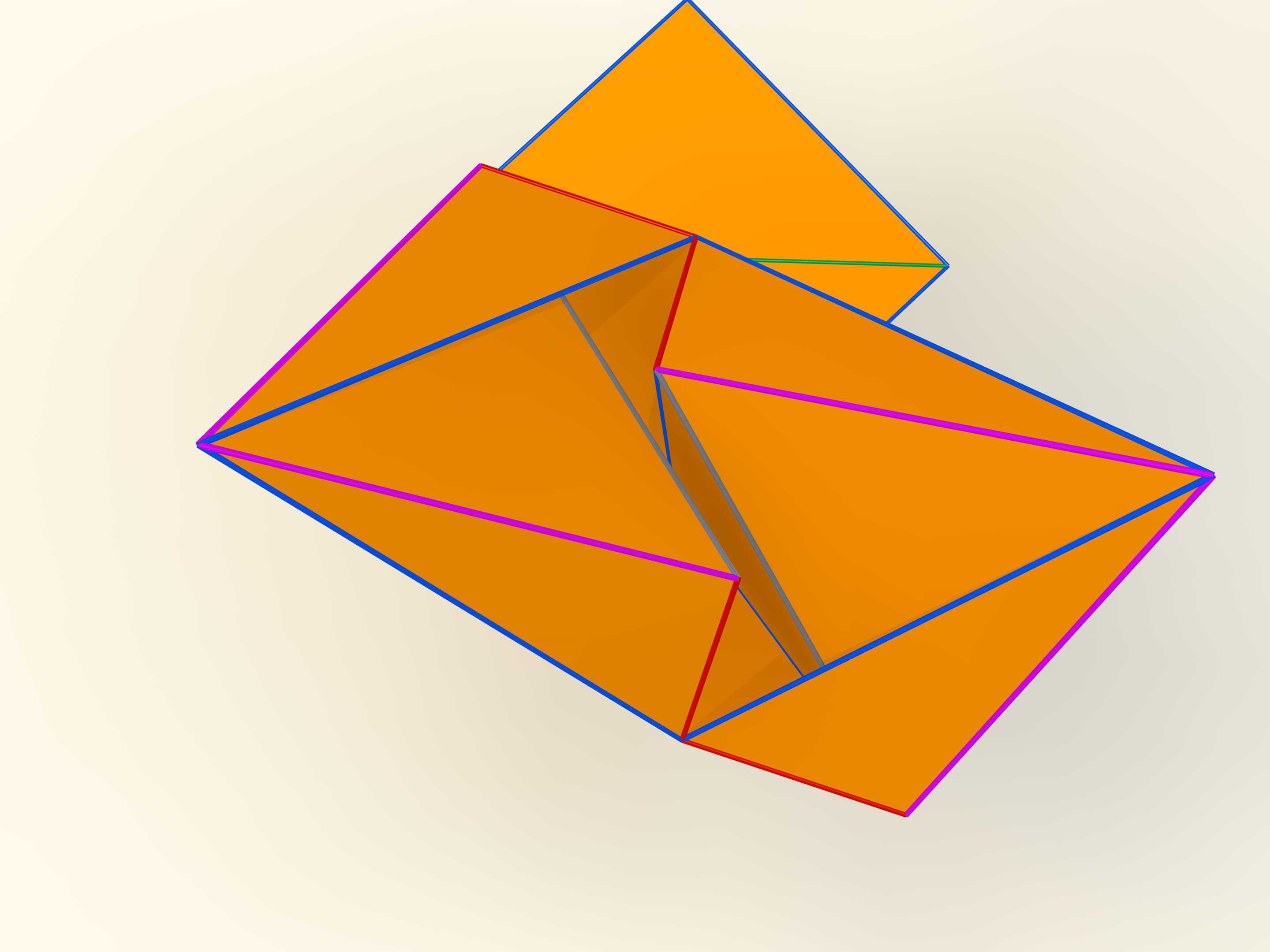
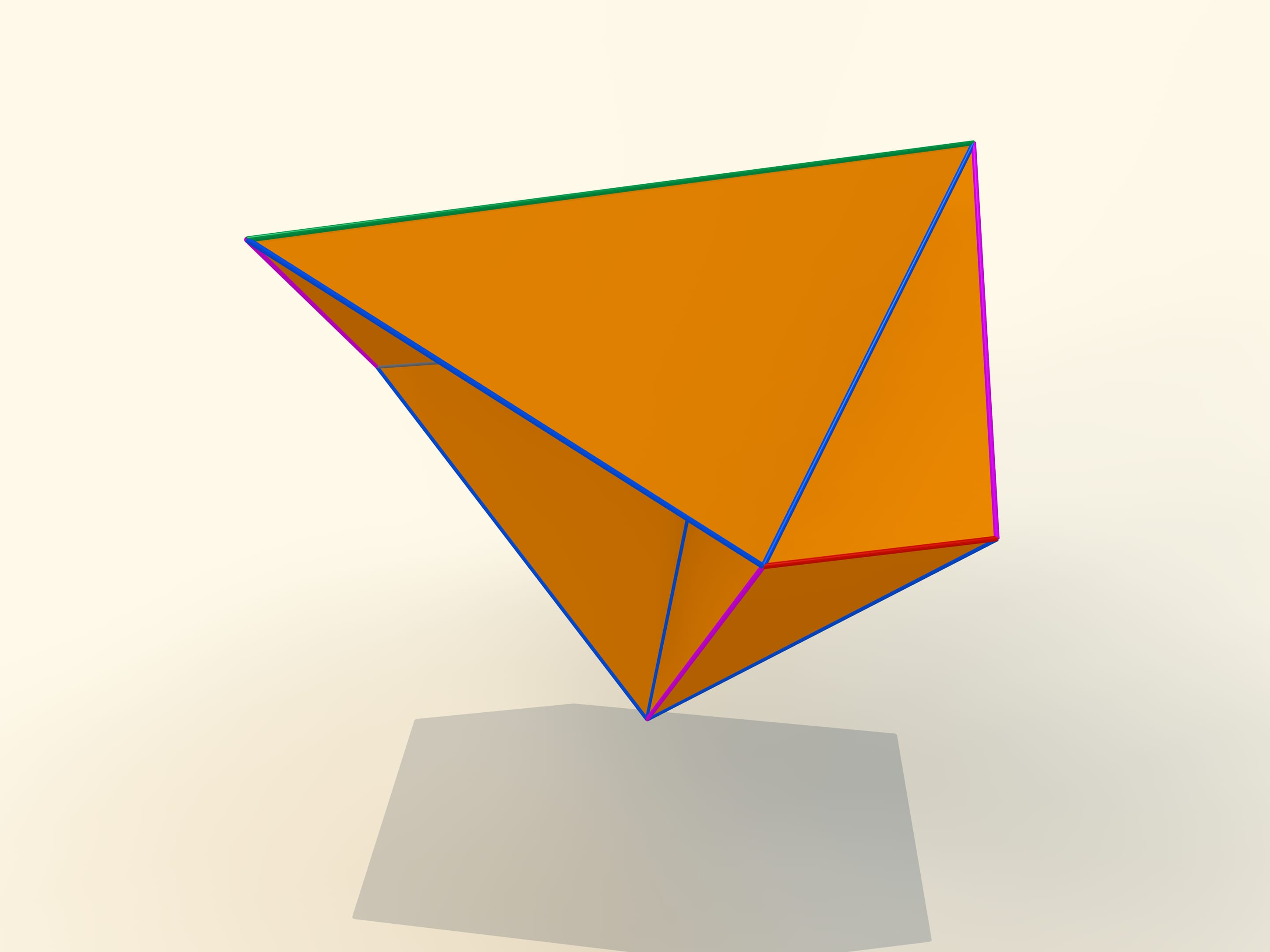
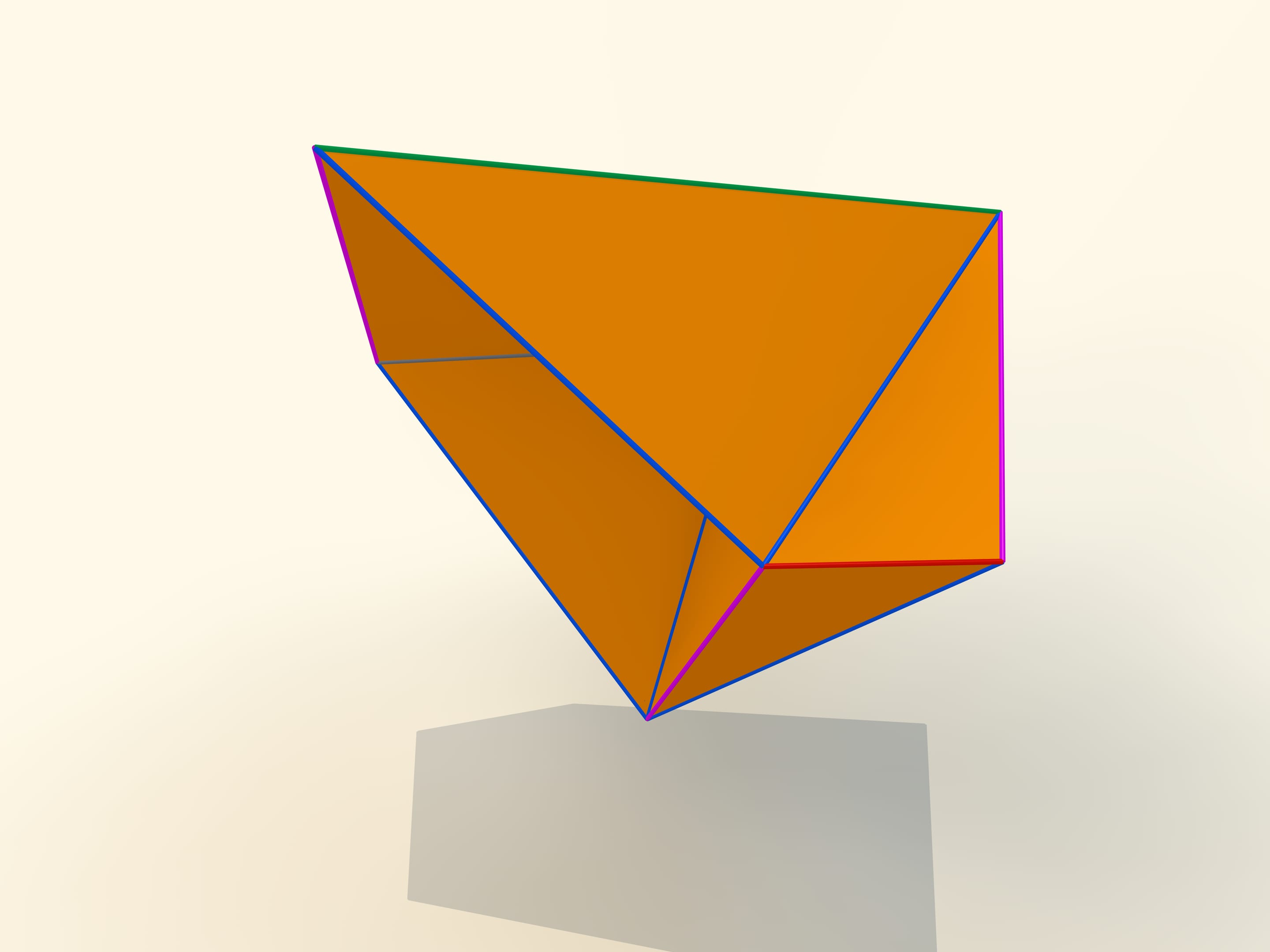
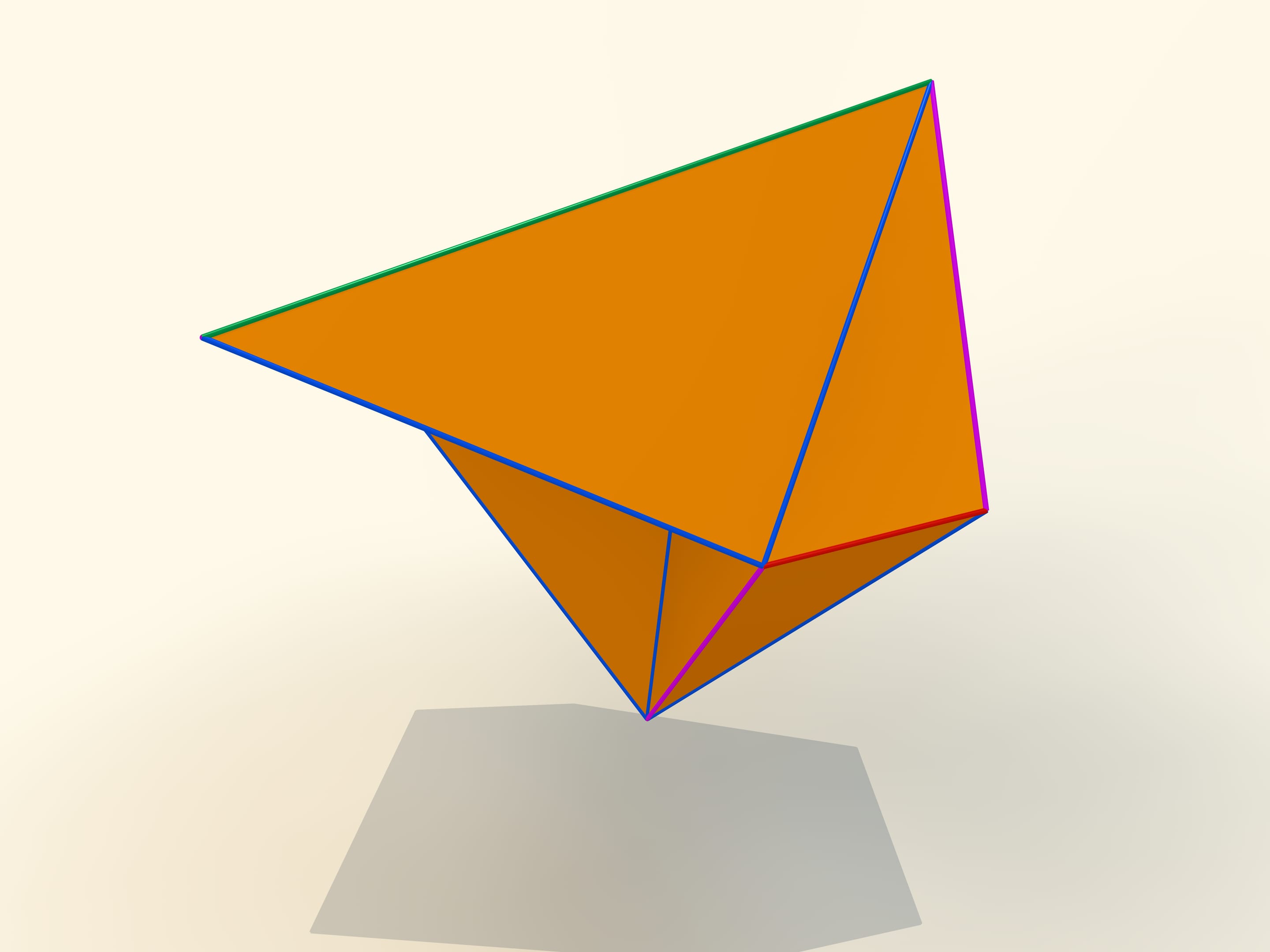
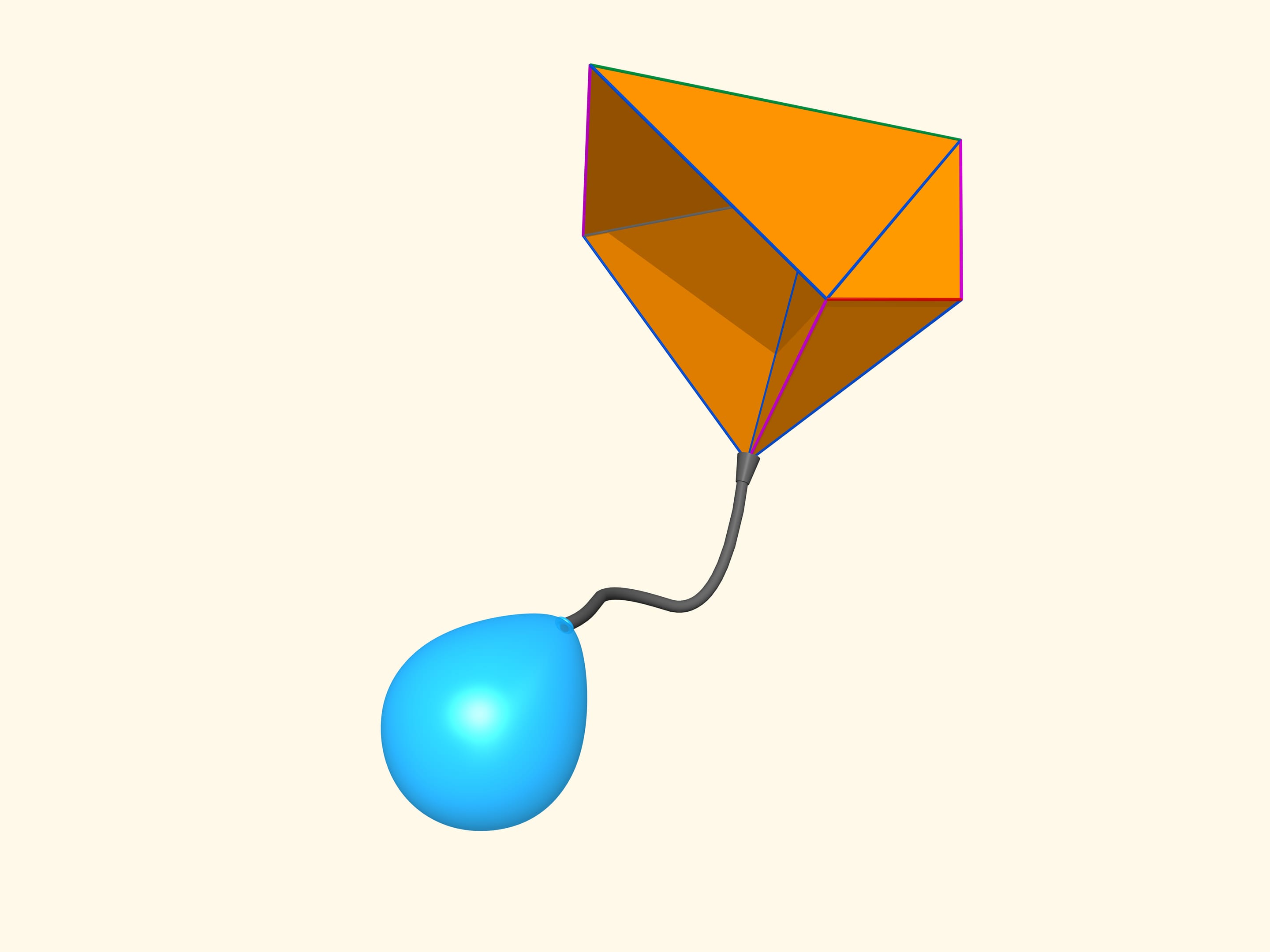
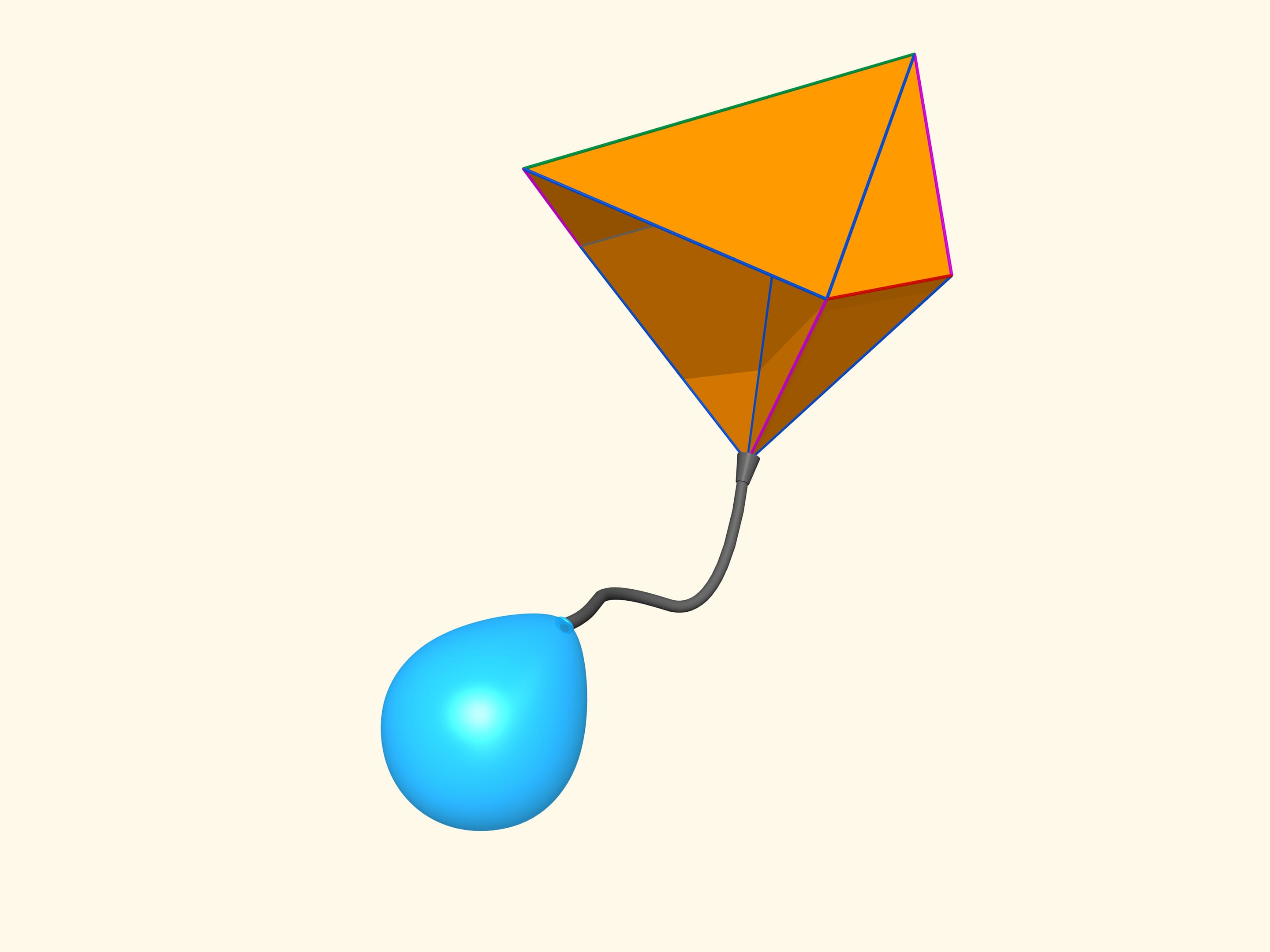
Первые математические примеры изгибаемых многогранников, естественно, невыпуклых, а также классификация этих объектов были построены бельгийским инженером Рене Брикаром в 1897 году. Математические, потому что эти многогранники были не только невыпуклыми, но и самопересекающимися — их грани пересекались друг с другом. С точки зрения математика, это тоже многогранник, однако реализовать его в нашем трёхмерном пространстве невозможно. В 1975 году американский математик Роберт Коннелли придумал, как избавиться от пересечения (так называемые «зарубки Коннелли»), и появились «настоящие» изгибаемые многогранники. Самый простой, известный на сегодняшний день, состоящий из 9 вершин, 17 рёбер и 14 граней, будет сейчас построен. Его в 1978 году придумал немецкий математик Клаус Штеффен.
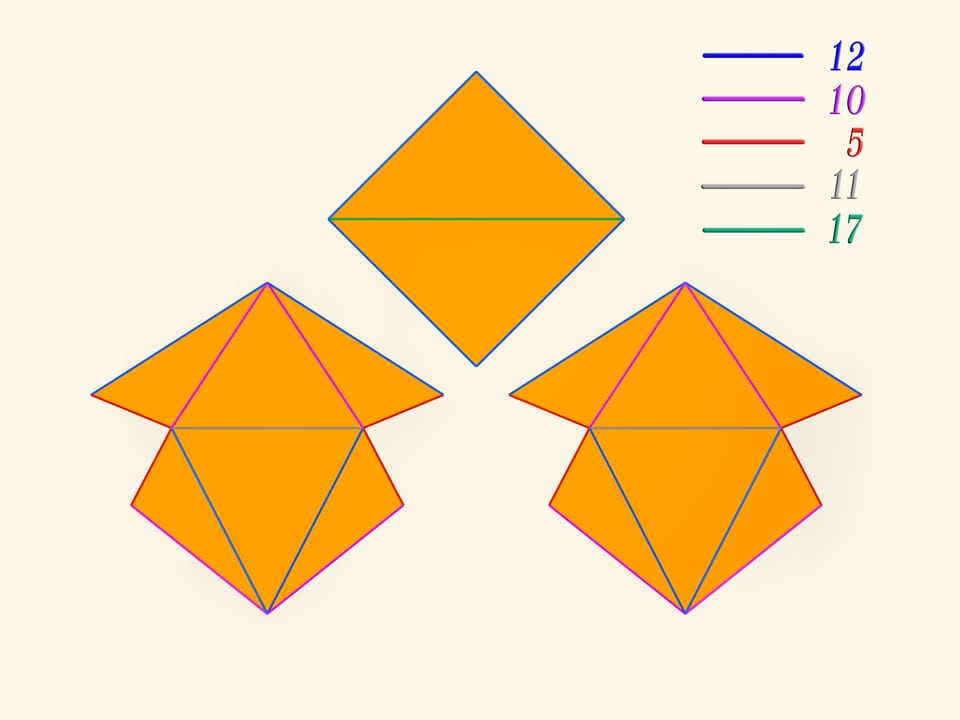
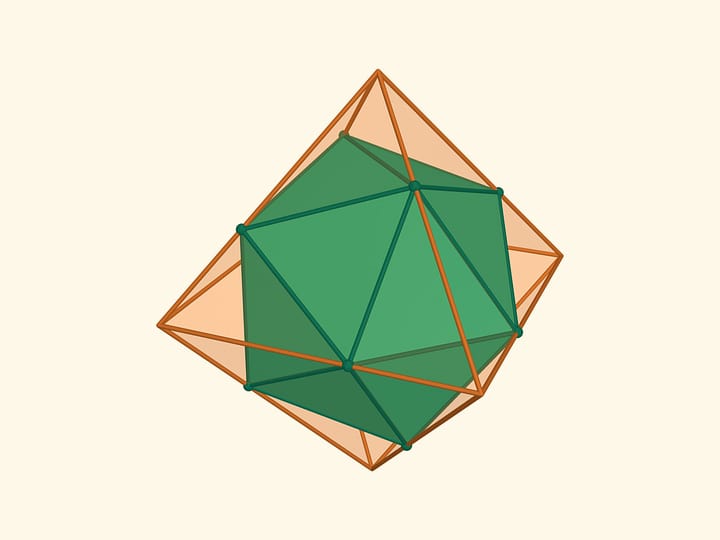
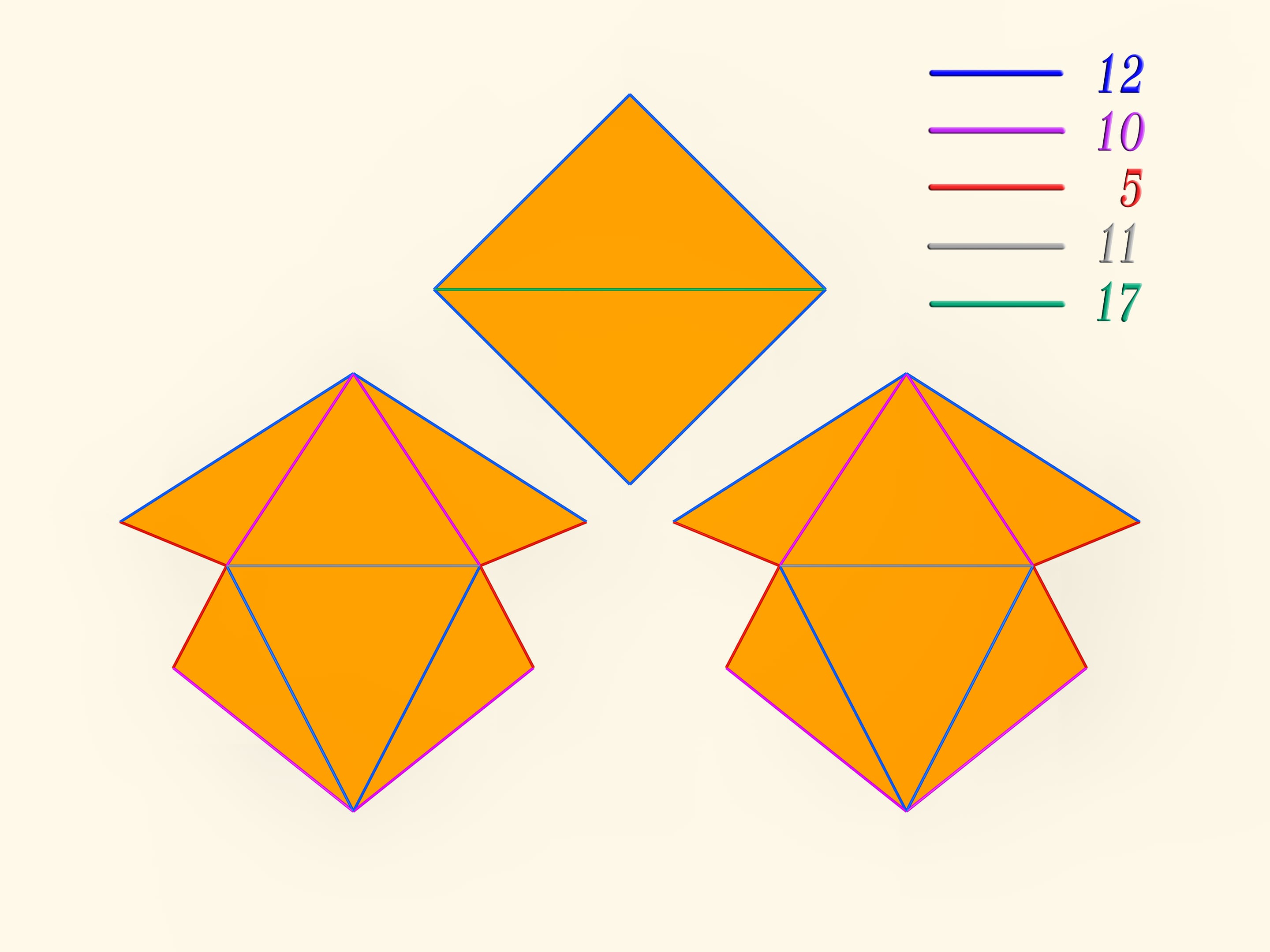
Развёртка многогранника Штеффена состоит из двух одинаковых частей и «крышки». Одинаковые части развёртки — разные фазы одного и того же изгибаемого октаэдра Брикара с удалёнными двумя гранями (чтобы избавиться от самопересечения). А крышка обеспечивает их синхронное изгибание.
Даже помня внешний вид развёртки, но не зная длин рёбер, построить такой многогранник самому сложно: возможность изгибаться — это всё же исключение для многогранников, и таких относительно мало.
Можно показать, что несамопересекающийся многогранник с 7 и меньшим числом вершин изгибаться не может. Описанный изгибаемый многогранник Штеффена имеет 9 вершин. А вот бывает ли изгибаемый несамопересекающийся многогранник с 8 вершинами до сих пор неизвестно.
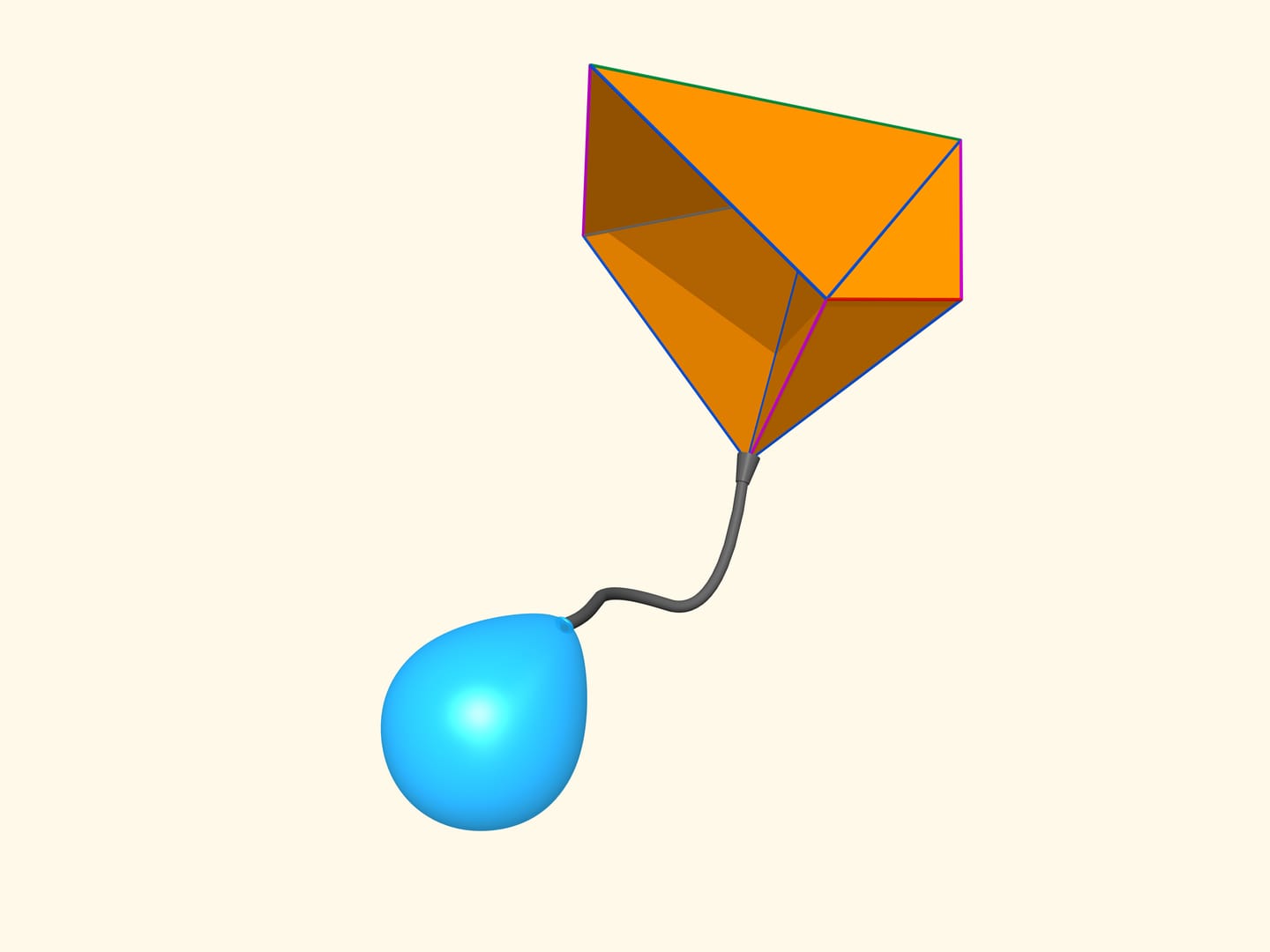
Когда математики поняли, что изгибаемые многогранники бывают, возник вопрос, получивший название «гипотезы кузнечных мехов». За счёт чего кузнечные мехи раздувают угли? За счёт чего играет гармонь? Их принцип действия основан на изменении внутреннего объёма. А что же изгибаемые многогранники — будет ли меняться их объём при изгибании? Можно ли кузнечные мехи или гармонь делать не из кожи, а из жёстких пластин, в виде многогранников?
В конце XX века полный ответ на этот вопрос был найден российским математиком И. Х. Сабитовым. Оказывается, для объёмов многогранников, в том числе изгибаемых, верен некий аналог формулы Герона для площади треугольника. А именно, существует такой многочлен одной переменной, что его коэффициенты зависят только от длин рёбер многогранника, а объём есть корень этого многочлена. Так как рёбра у изгибаемых многогранников не меняются, то и сам этот многочлен, а значит, и его корни не меняются при изгибании самого многогранника. Но различные корни многочлена одной переменной суть конкретные числа, расположенные друг от друга на каком-то расстоянии. При малых шевелениях многогранника объём может меняться мало, поэтому не может резко перепрыгнуть из одного корня многочлена в другой. Значит, объём изгибаемых многогранников не меняется при их изгибаниях!
Мы рассмотрели вопрос об изгибаемых многогранниках в обычном трёхмерном пространстве. А что происходит в бóльших размерностях?
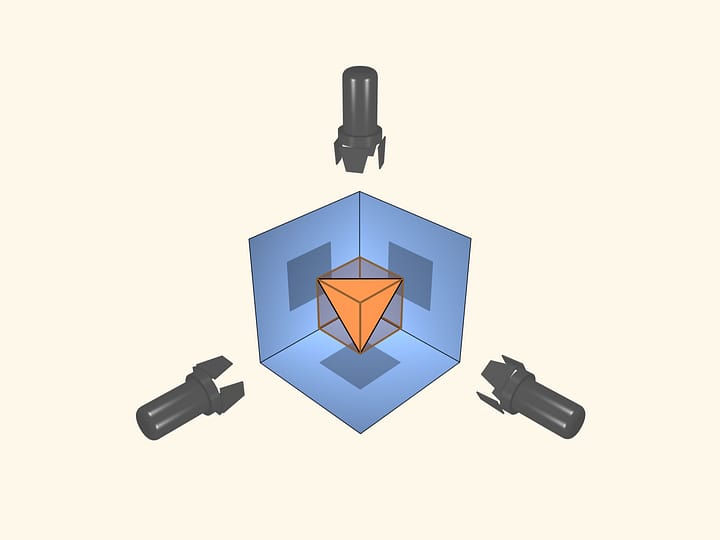
В цикле работ 2012—2015 годов российский математик Александр Гайфуллин обобщил результаты на многомерные пространства. Несложно показать, что в пространстве размерности $n$ изгибаемый многогранник не может иметь меньше $2n$ вершин. А. Гайфуллин доказал существование изгибаемых многогранников в пространствах любой размерности описав все (в том числе самопересекающиеся) $n$—мерные изгибаемые многогранники ровно с $2n$ вершинами. Причём сделал это в каждом из трёх многомерных пространств постоянной кривизны: евклидовом — пространстве нулевой кривизны, являющимся обобщением нашего обычного пространства; пространстве Лобачевского — пространстве постоянной отрицательной кривизны; сферическом — пространстве постоянной положительной кривизны.
В пространствах постоянной положительной кривизны объём изгибаемых многогранников уже не обязательно постоянен (даже в размерности 3). А в пространствах Лобачевского (постоянной отрицательной кривизны) постоянство объёма удалось доказать лишь в размерностях 3, 5, 7, … (нечётных). В чётных же размерностях примеров изгибаемых многогранников с изменяющимся объёмом неизвестно, но и доказать его постоянство тоже пока не удалось.
В 2017 году было доказано, что любой изгибаемый многогранник в процессе изгибания остаётся равносоставленным с самим собой (в частности, со своим начальным положением). Это означает, что если взять два многогранника — два положения данного изгибаемого многогранника — и заполнить их, то один многогранник можно распилить на многогранные куски, из которых составляется второй. В четырёхмерном евклидовом пространстве дела обстоят так же, а вот в евклидовых пространствах больших размерностей — неизвестно. В неевклидовых пространствах аналогичные вопросы приводят к сложным нерешённым задачам алгебраической $K$-теории
Да и в евклидовых пространствах остаются нерешённые задачи. Например, в размерностях начиная с 4 все известные изгибаемые многогранники — самопересекающиеся. Существуют ли несамопересекающиеся, — неизвестно.
Литература
Долбилин Н. П. Жемчужины теории многогранников. — М. : МЦНМО, 2000.
Долбилин Н. П. Три теоремы о выпуклых многогранниках.
Часть 1 // Квант. — 2001. — № 5. — С. 7—12.
Часть 2 // Квант. — 2001. — № 6. — С. 3—10.
Сабитов И. Х. Объёмы многогранников. — М. : МЦНМО, 2002.
Залгаллер В. Непрерывно изгибаемый многогранник // Квант. — 1978. — № 9. — С. 13—19.