Замечательная формула Эйлера $V-E+F=2$ выражает зависимость между числом вершин ($V$, от слова vertices), числом рёбер ($E$, edges) и числом граней ($F$, faces) выпуклого многогранника. В пространстве с координатами $(V, E, F)$ это соотношение, будучи линейным, задаёт плоскость. Плоскость, на которой лежат все выпуклые многогранники! Назовём её плоскостью Эйлера.
Все ли точки с целыми положительными координатами на этой плоскости отвечают каким-то многогранникам? Другими словами, является ли условие $V-E+F=2$ не только необходимым, но и достаточным для существования многогранника с данным количеством вершин, рёбер, граней?
Нет, не все, так как есть четыре очевидных ограничения.
Не бывает многогранника меньше чем с четырьмя вершинами и чётырьмя гранями, значит $V\ge 4$ и $F\ge 4$. Оба равенства реализуются для тетраэдра (см. вкладку «Правильные многогранники»).
У каждой грани хотя бы три ребра, а каждое ребро принадлежит ровно двум граням, поэтому $2E \ge 3F$. Это неравенство обращается в равенство, если все грани являются треугольниками. На плоскости Эйлера это неравенство задаёт прямую, на которой лежат, например, октаэдр и другие бипирамиды (см. вкладку «Серии многогранников»).
В каждой вершине сходятся не менее трёх рёбер, а каждое ребро соединяет ровно две вершины, поэтому $2E \ge 3V$. Это неравенство обращается в равенство, если в каждой вершине сходятся ровно по три ребра, т. е. по три грани (такие многогранники называются простыми). На плоскости Эйлера это неравенство задаёт прямую, на которой лежат, например, куб и другие призмы (см. вкладку «Серии многогранников»).
Система перечисленных четырёх неравенств $$4 \le V \le \frac{2}{3} E \hspace{5ex} \text{и} \hspace{5ex} 4 \le F \le \frac{2}{3} E$$ выделяет на плоскости Эйлера угол. Вершина угла — точка, отвечающая тетраэдру. Оказывается, других ограничений, кроме перечисленных очевидных, нет! Все целые точки плоскости Эйлера внутри этого угла действительно реализуются выпуклыми многогранниками — это следует из теоремы Штайница, относящейся к комбинаторной геометрии.
Обратим внимание, что нет взаимно однозначного соответствия целых точек на плоскости Эйлера и многогранников: точке может соответствовать несколько многогранников.
На картинках, представляющих многогранники на плоскости Эйлера, в самой формуле Эйлера $V-E+F=2$ и в полученных неравенствах, задающих угол, можно заметить симметрию: она соответствует перестановке $V$ и $F$. Всё это проявление двойственности для выпуклых многогранников.
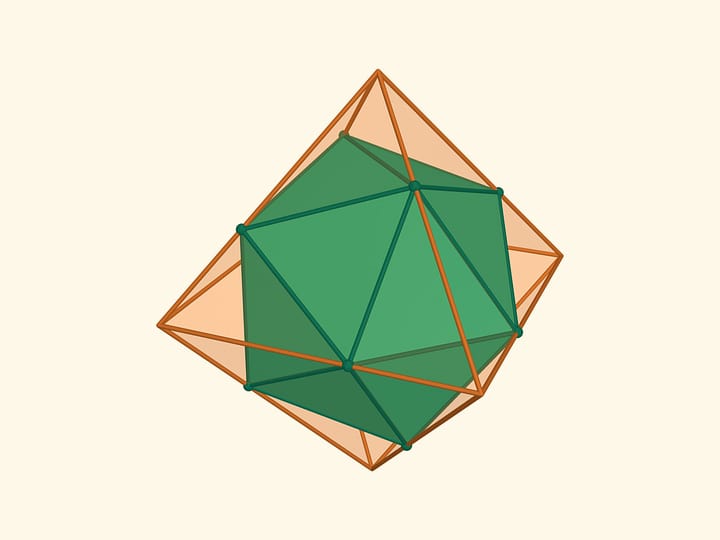
Для правильных многогранников: центры граней куба являются вершинами октаэдра и наоборот; центры граней додекаэдра являются вершинами икосаэдра и наоборот; а тетраэдр — самодвойственный. Архимедовым телам (полуправильным многогранникам) двойственны каталановы тела (равногранные многогранники). В классических сериях: призмы двойственны с бипирамидами, антипризмы — с трапецоэдрами.
Написанное выше остаётся верным и для привычных невыпуклых многогранников. Тут, однако, есть нюансы. Если отметить точку $(V, E, F)$ для многогранника Силашши, то она не будет лежать на плоскости Эйлера. Дело в том, что этот многогранник не просто невыпуклый, но ещё и с дыркой — представляет собой полиэдральный тор. А двойка в правой части формулы Эйлера $V-E+F=2$ соответствует многогранникам без дыр, т. е. топологически эквивалентным сфере.
Формула $V-E+F=2$ была открыта Леонардом Эйлером в 1750 году. Приведём цитату из книги И. Лакатоса «Доказательства и опровержения» (сноска на стр. 12)::
Первоначальной его задачей было дать классификацию многогранников. На трудность этого было указано в заключении издателя: «В то время как в плоской геометрии многоугольники легко могут быть классифицированы по числу сторон, которое, конечно, всегда будет равно числу углов, в стереометрии классификация многогранников представляет собой значительно более трудную задачу, так как только одно число граней недостаточно для этой цели». Ключом к полученному Эйлером результату было как раз введение понятий вершины и ребра; он первый указал на то, что кроме числа граней, число точек и линий на поверхности многогранника определяет его (топологический) характер.
Литература
Eulero L. Elementa doctrinae solidorum // Novi Commentarii academiae scientiarum Petropolitanæ. — 1752/53. — Volume 4. — P. 109—140. — [Написано: 1750; Enestrom Number: 230; Fuss Index: 318].
Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — [Глава 10 «Пять платоновых тел»].
Пойа Д. Математика и правдоподобные рассуждения. — М.: ИЛ, 1957. — [Т. 1. Глава III «Индукция в пространственной геометрии»].
Шубин М. Топология и... рельеф местности // Журнал «Квант». — 1982. — № 8. — Cтр. 10—15.
Мерзон Г. Игры Конвея, рисунки Эйлера и прочие проблемы // Журнал «Квантик». — 2014. — № 7. — Стр. 18—22.
Гайфуллин А. А. Теорема Штайница: курс лекций на летней школе «Современная математика» имени Виталия Арнольда 2023 года. — https://mathnet.ru/present39754
Лакатос И. Доказательства и опровержения: как доказываются теоремы. — М.: Наука, 1967.