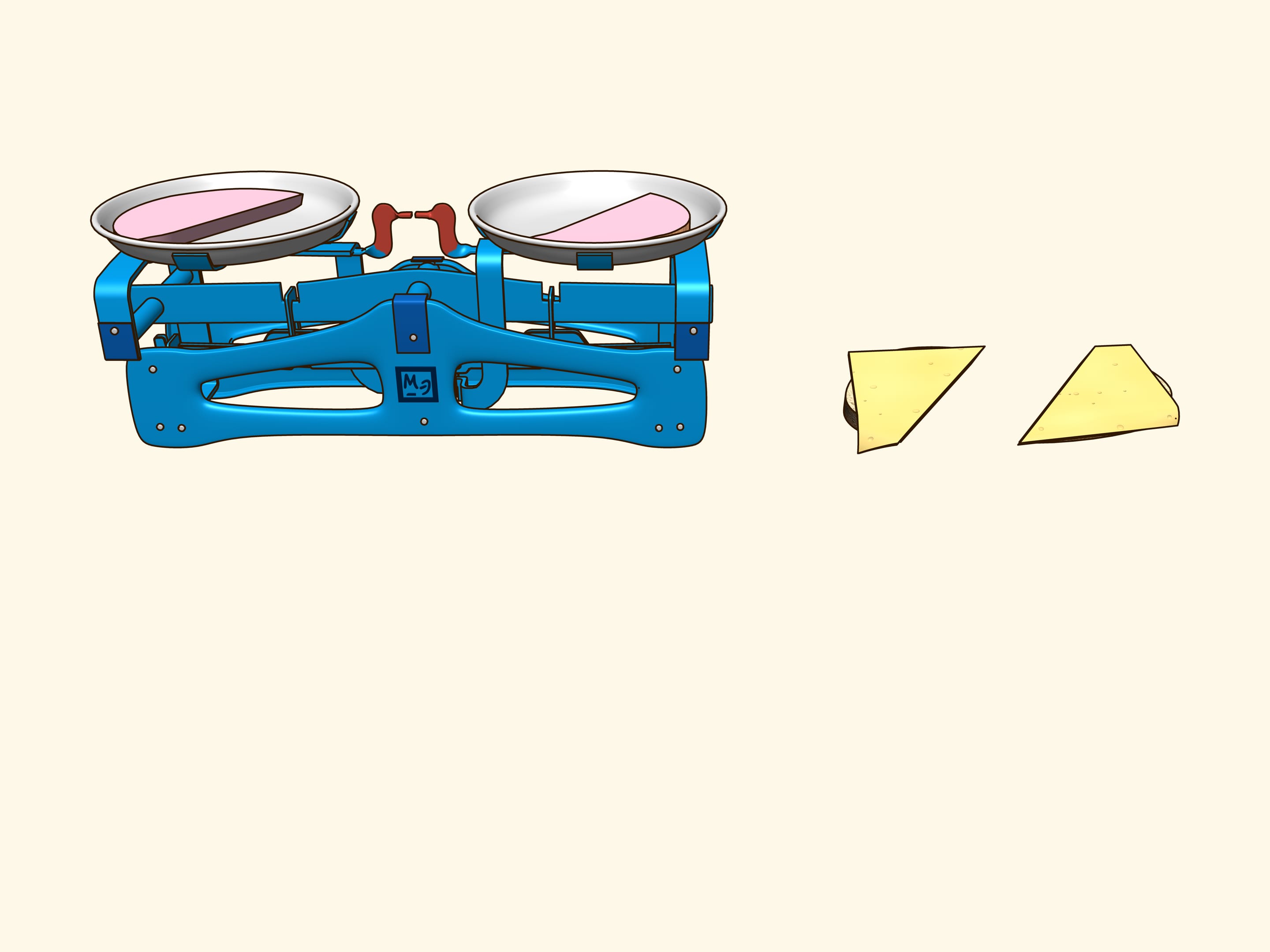
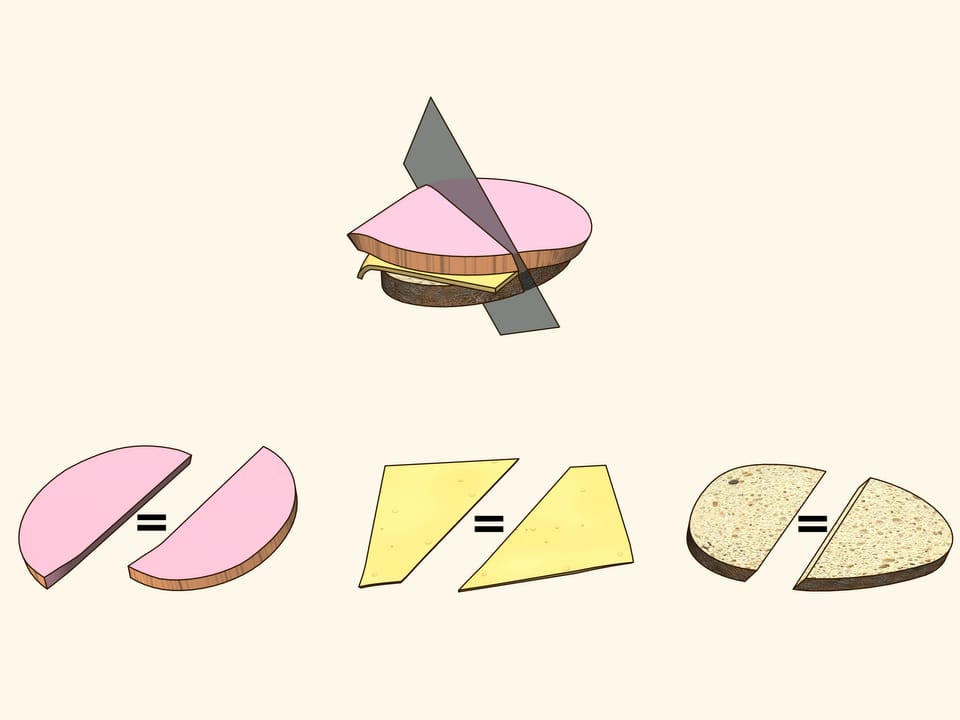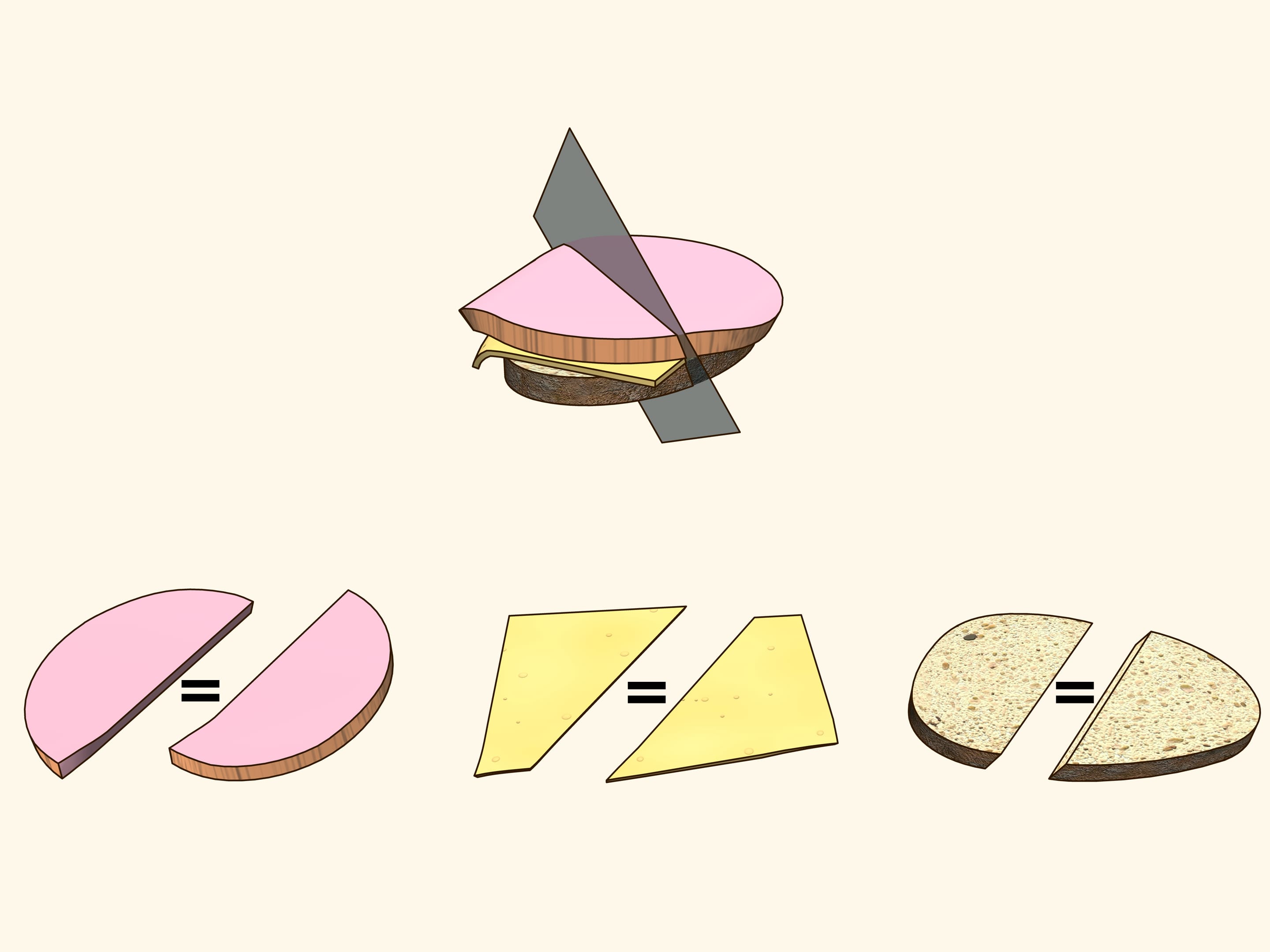Можно ли бутерброд из хлеба, сыра и колбасы разрезать одной плоскостью так, чтобы в обеих частях было одинаковое (по объёму) количество колбасы, а также одинаковое количество сыра и хлеба? Оказывается, что можно...
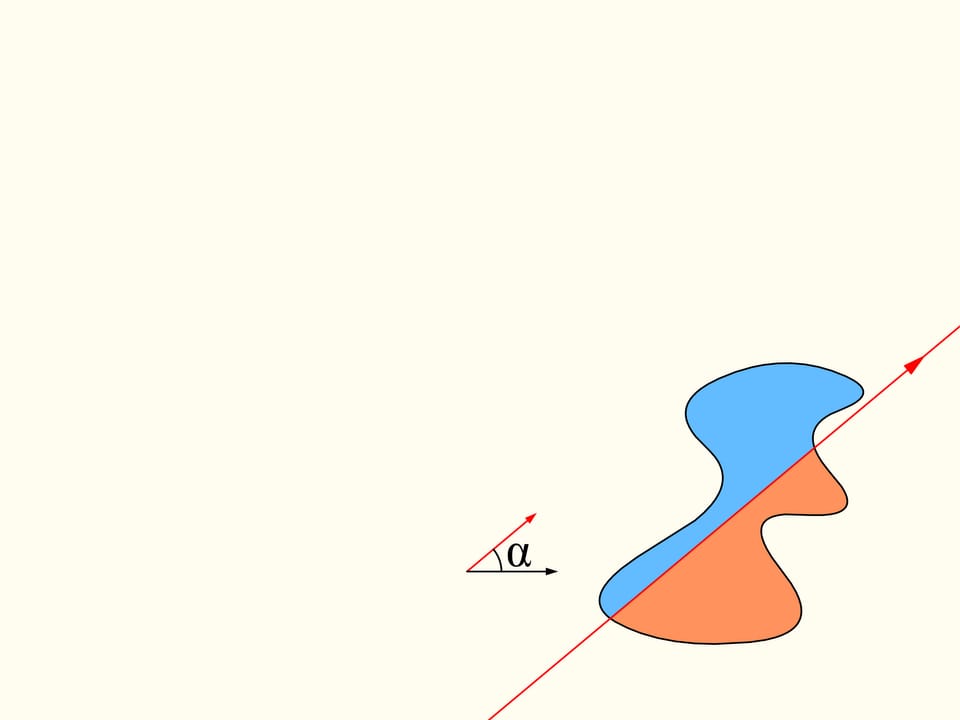
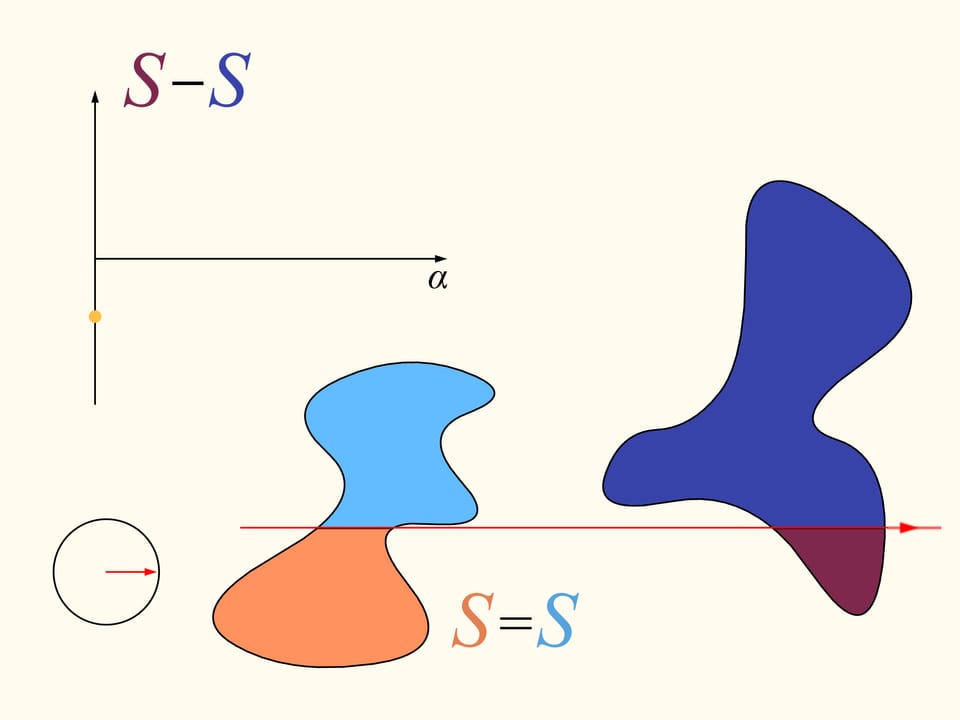
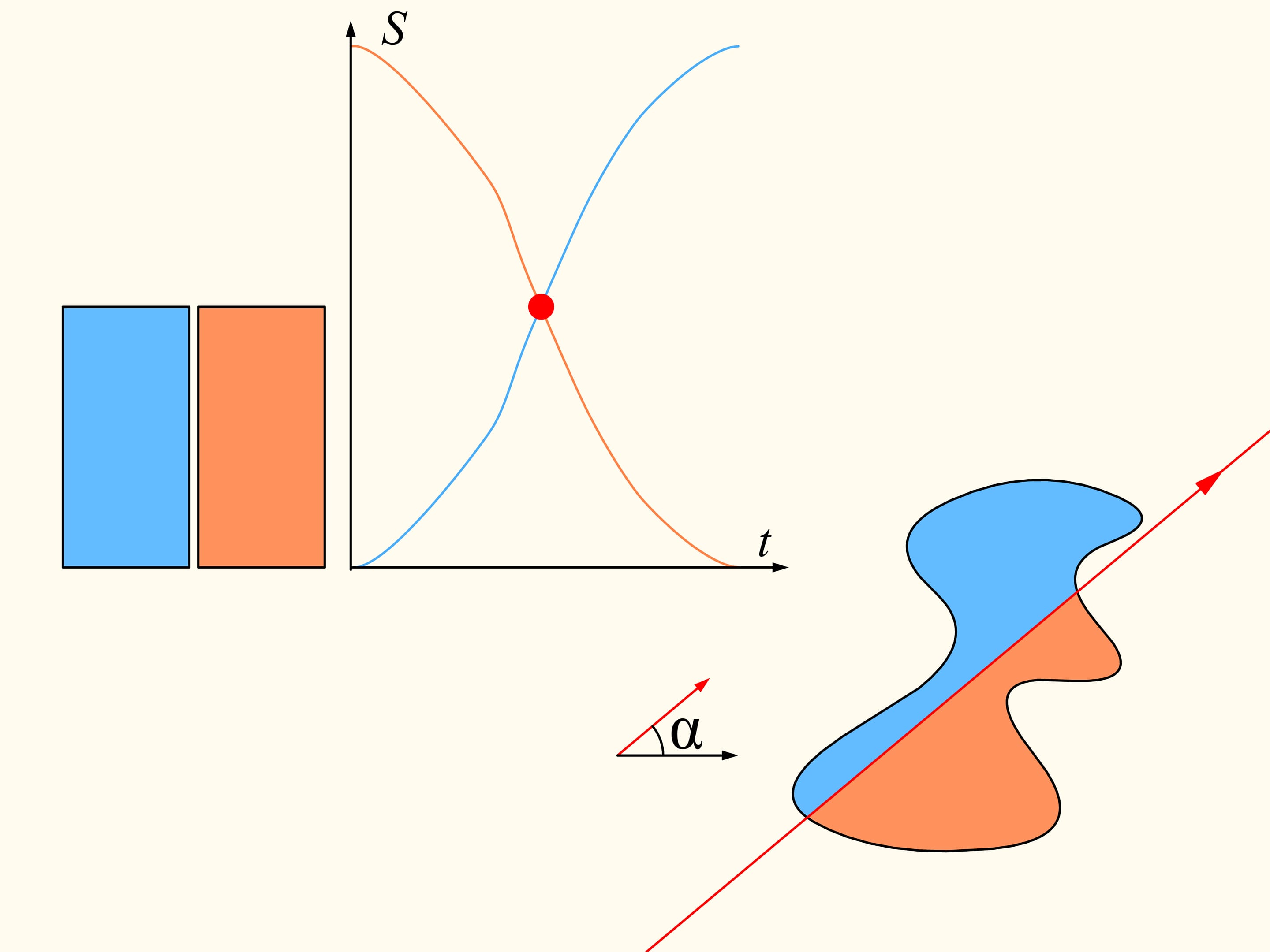
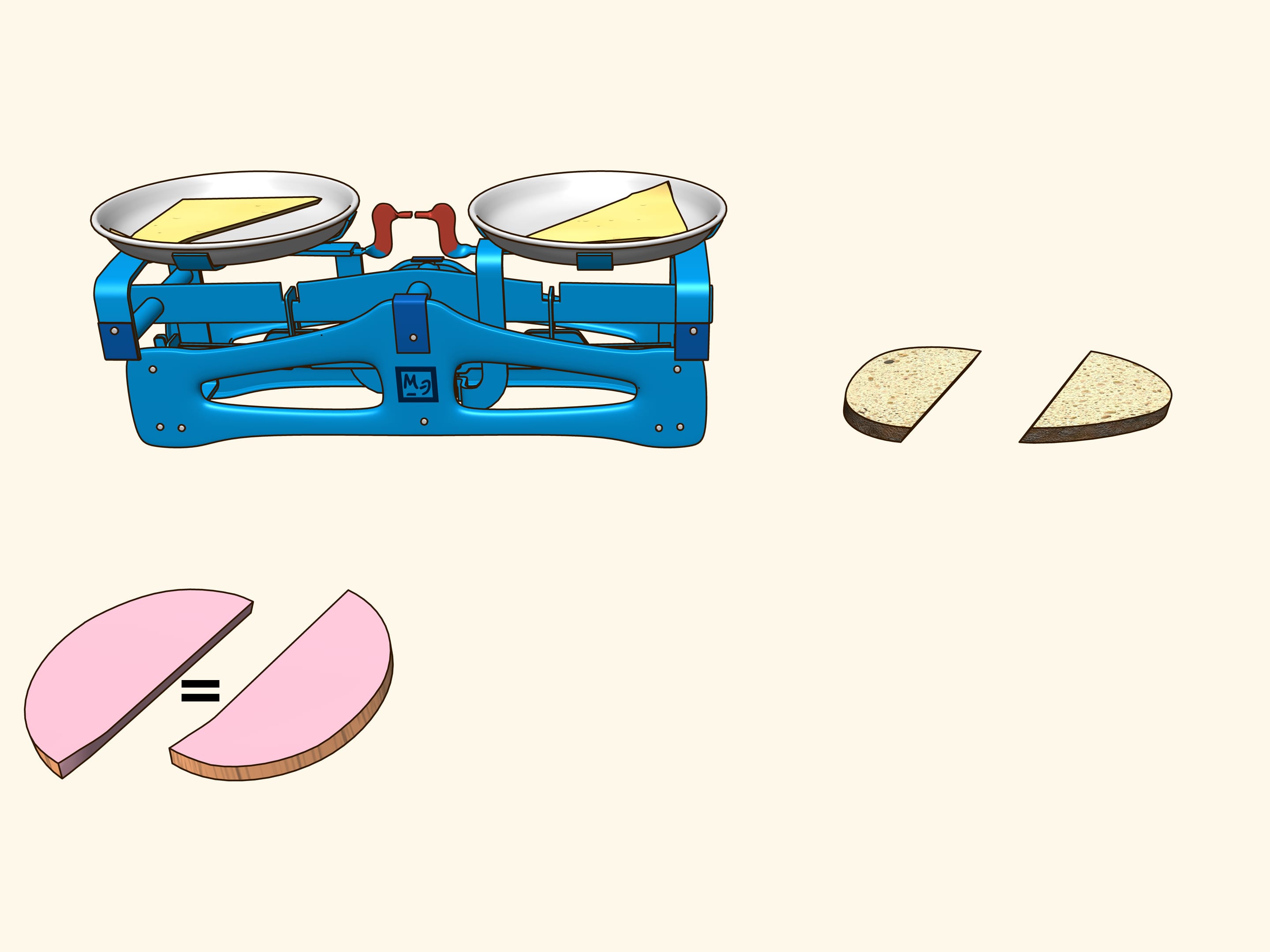
Рассмотрим сначала задачу в двумерном случае. На плоскости есть две произвольные области. Существует ли прямая, делящая ровно пополам по площади и первую область, и (одновременно) вторую?
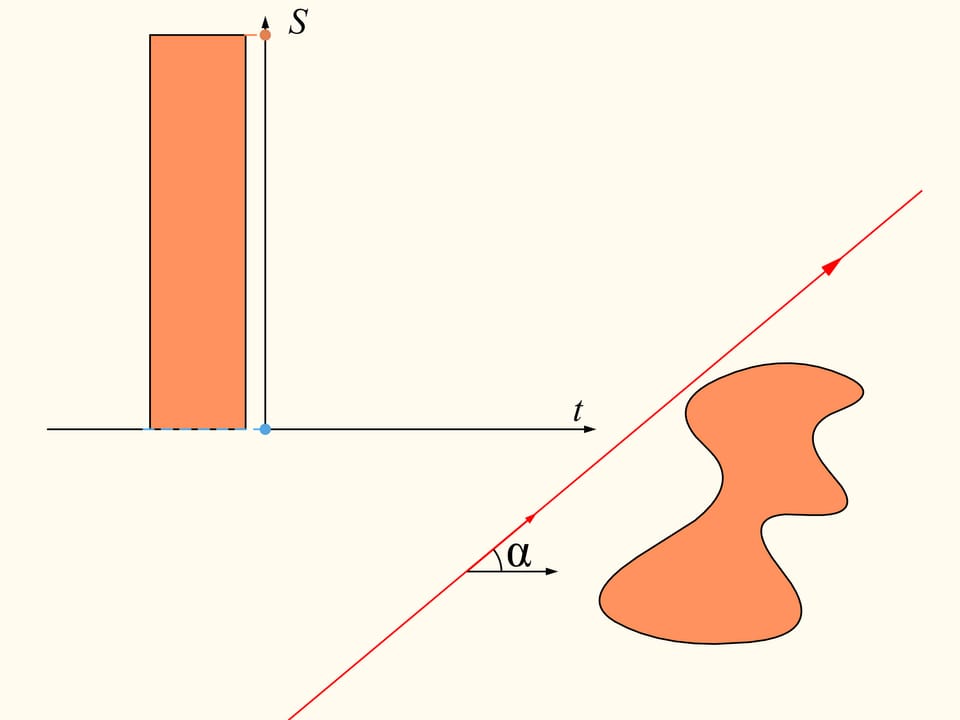
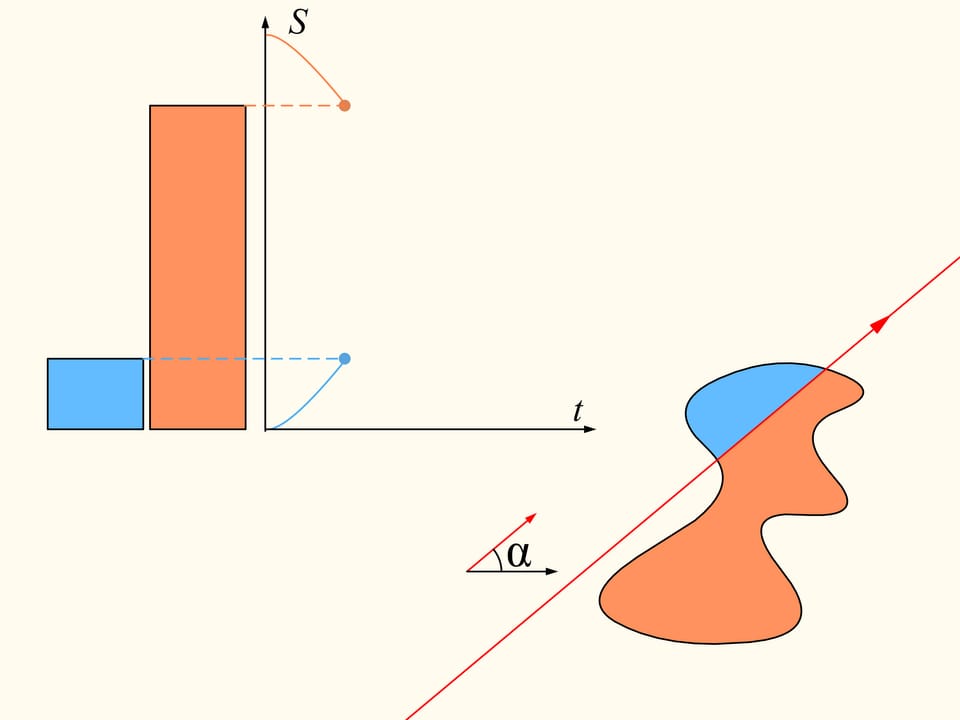
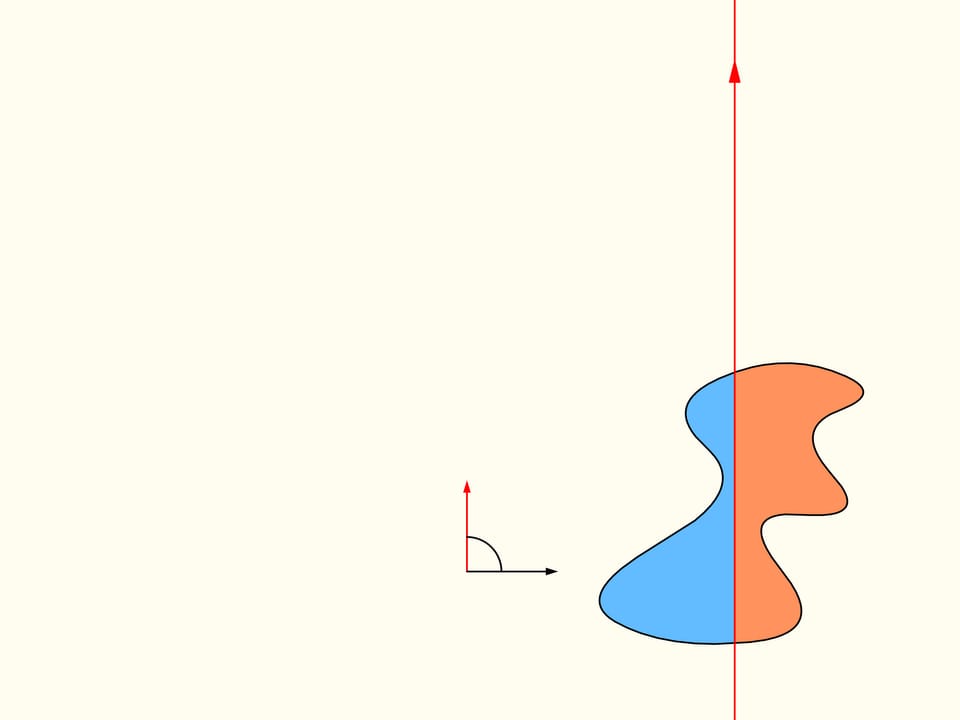
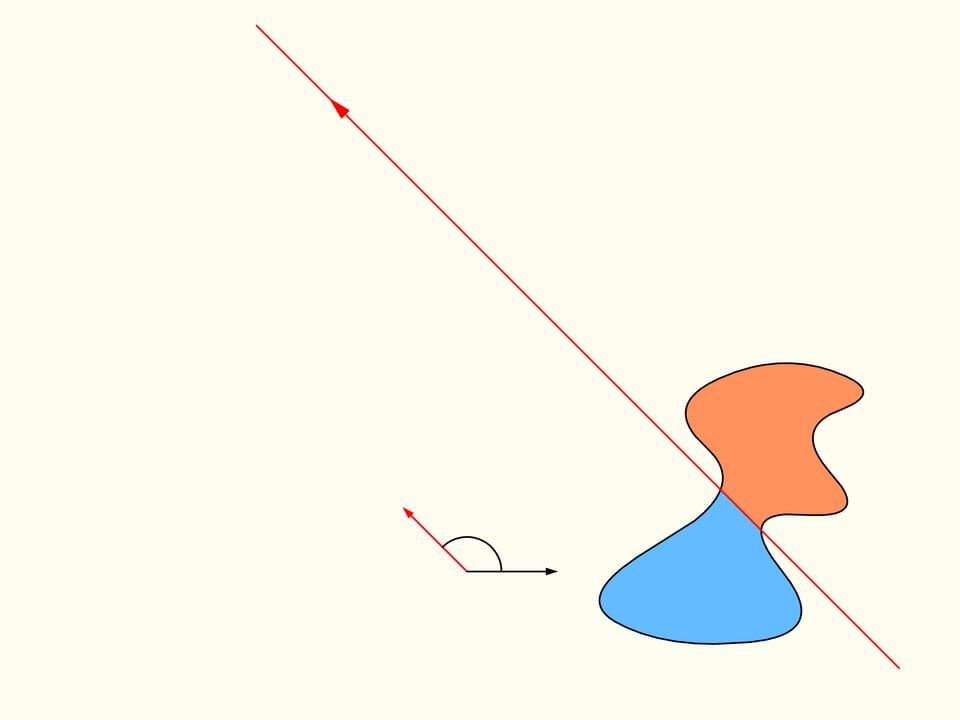
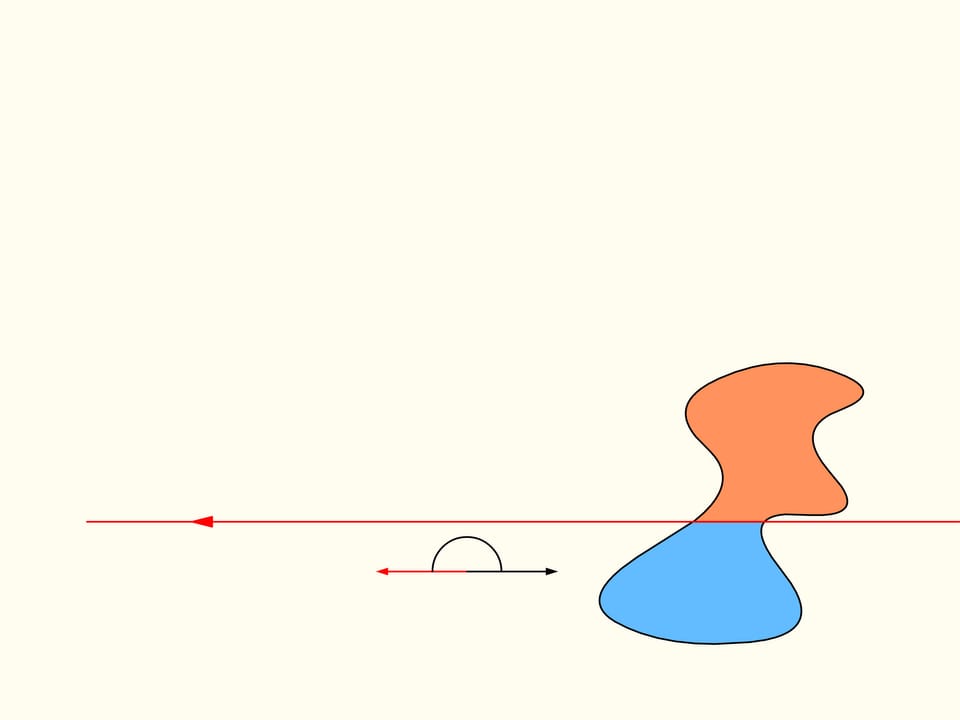
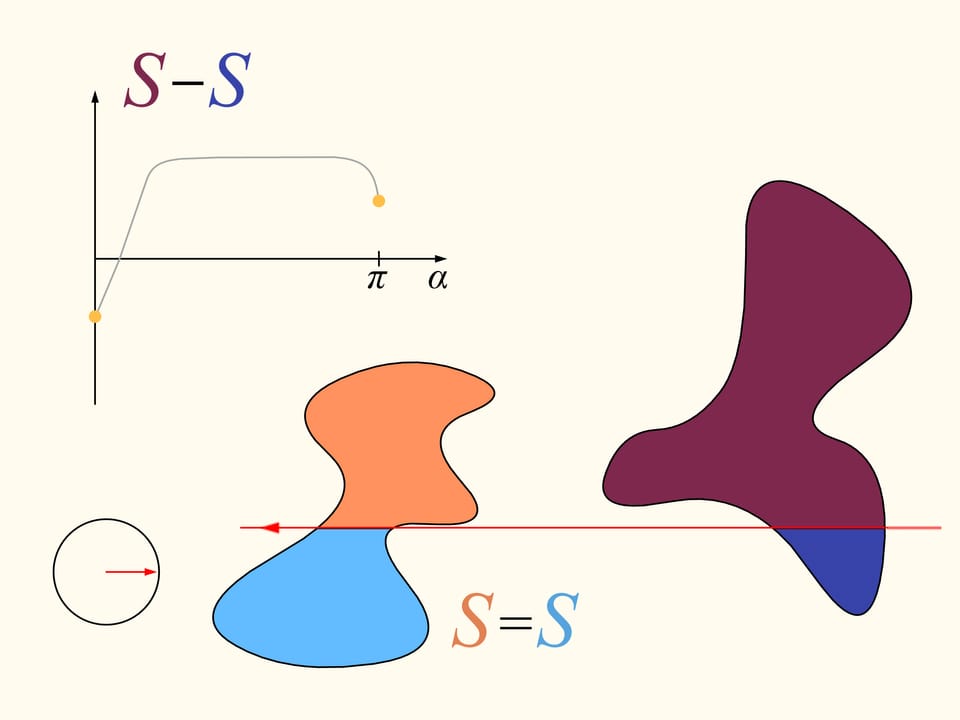
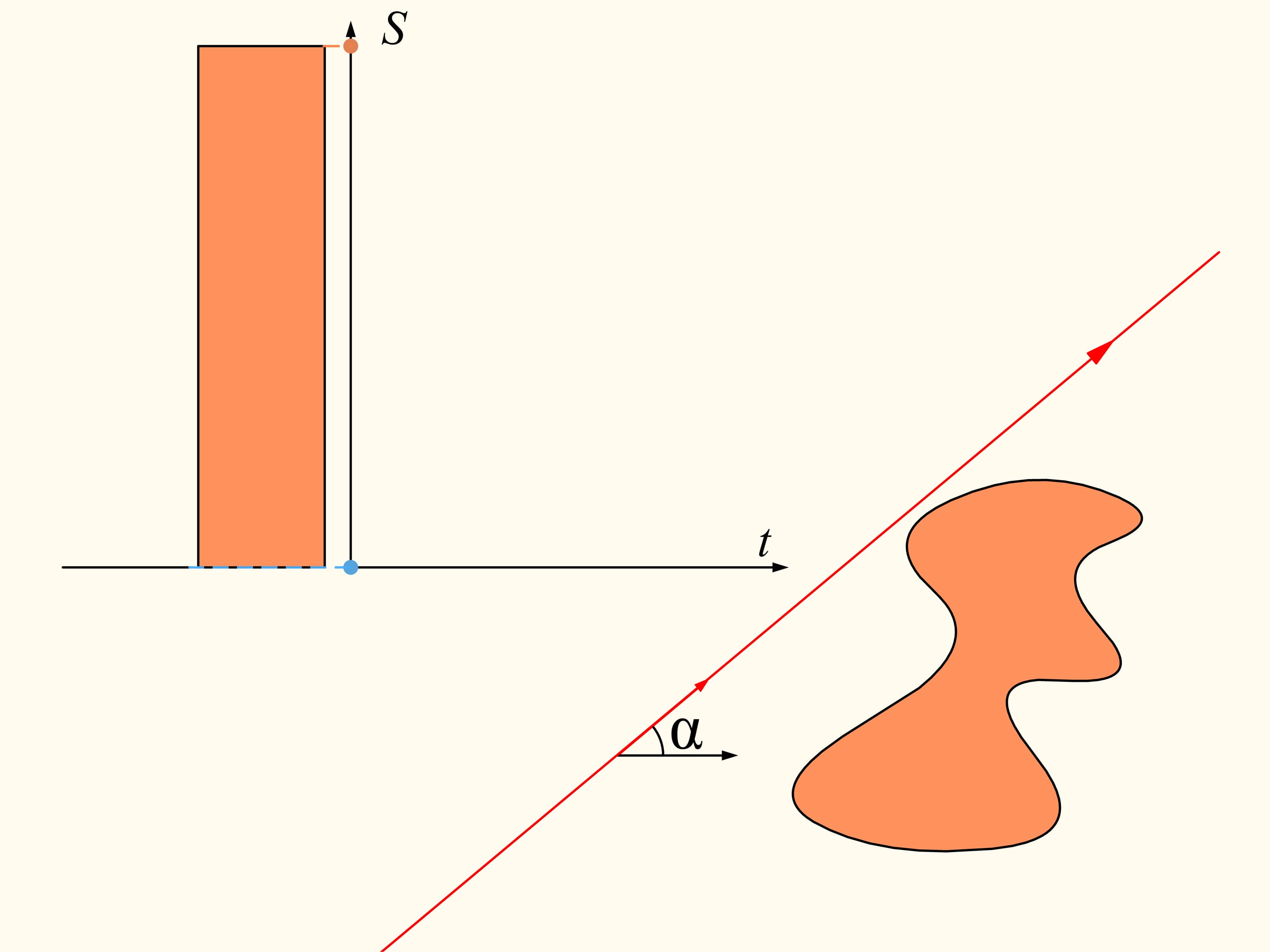
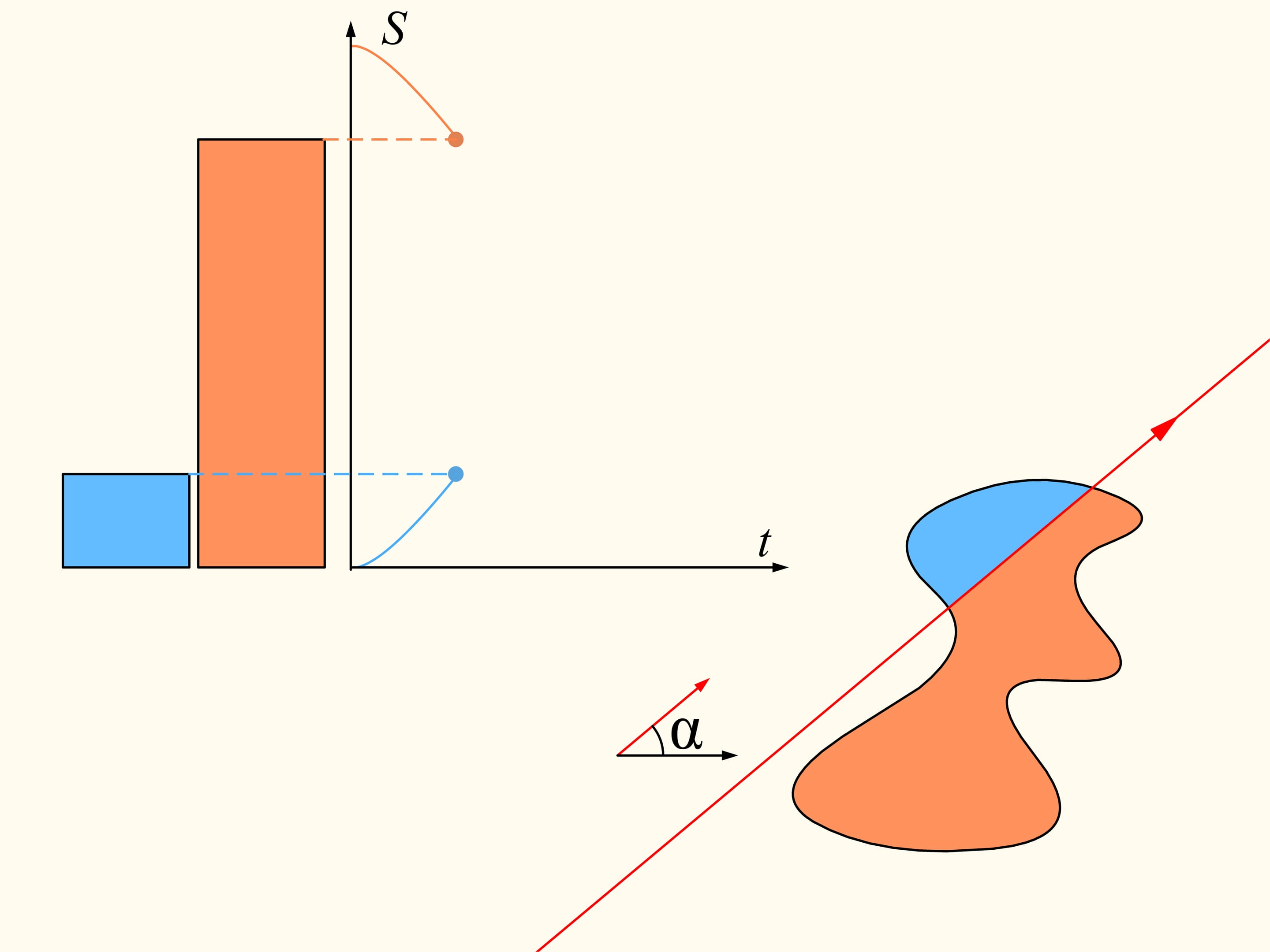
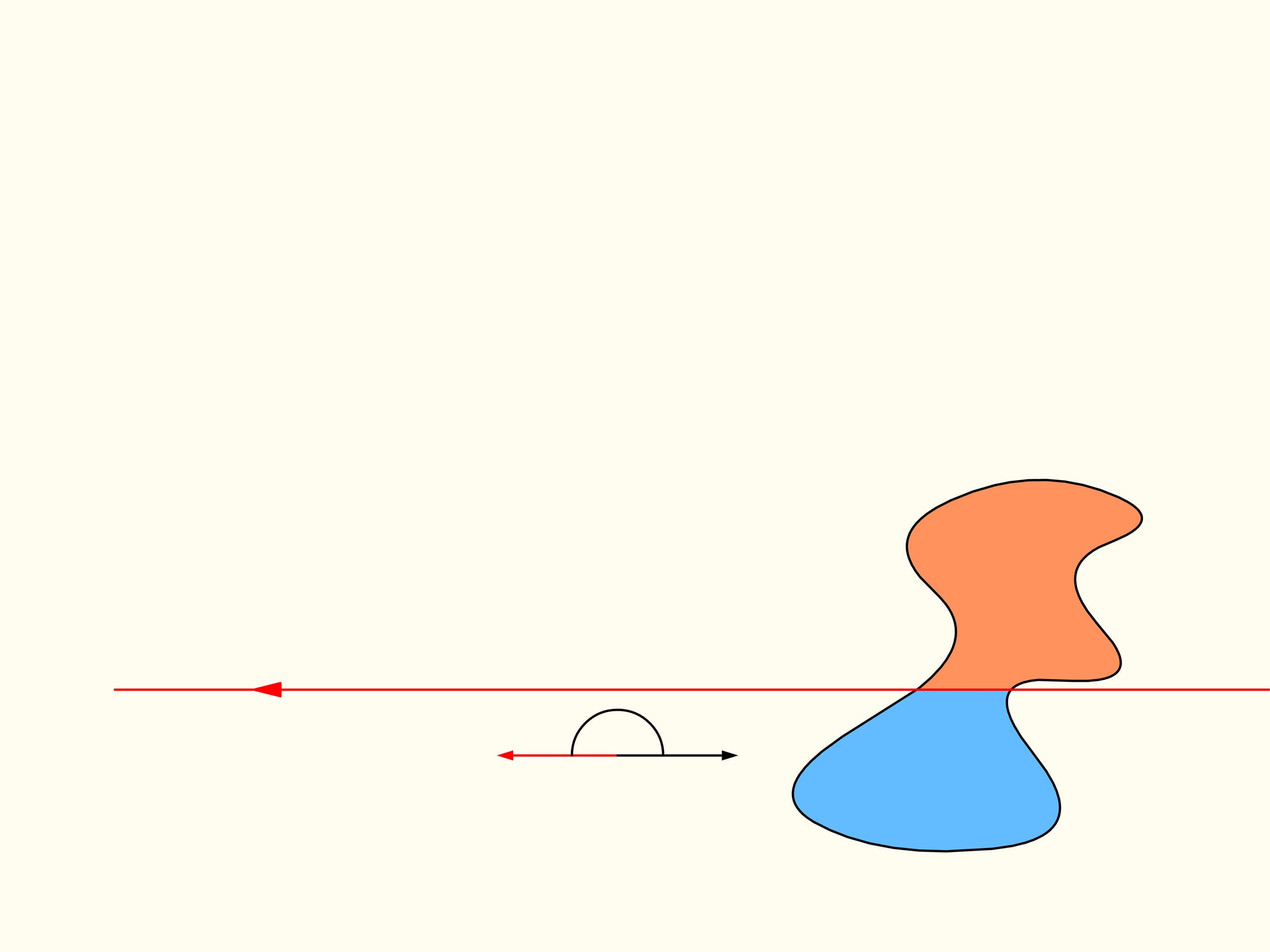
Докажем, что существует. Для этого поработаем вначале с одной из данных областей. Выберем произвольное направление. Существует ли прямая, параллельная этому направлению, которая делит область пополам? Покажем, что такая прямая для любого направления всегда найдётся. Проведём прямую выше области так, чтобы она была полностью с одной стороны. Будем строить графики — площадь области справа и слева от прямой (она у нас направленная, поэтому «право» и «лево» определены). Сейчас вся область справа от прямой, и, значит, один столбец соответствует полной площади кляксы, а второй столбец — нулевой. Начнём двигать прямую вправо так, чтобы она всегда была параллельна выбранному направлению. По мере прохождения области площадь справа будет непрерывно уменьшатся, а площадь слева от прямой — непрерывно увеличиваться. В какой-то момент вся область останется слева. Синий столбец будет соответствовать полной площади области, а коричневый будет нулевым.
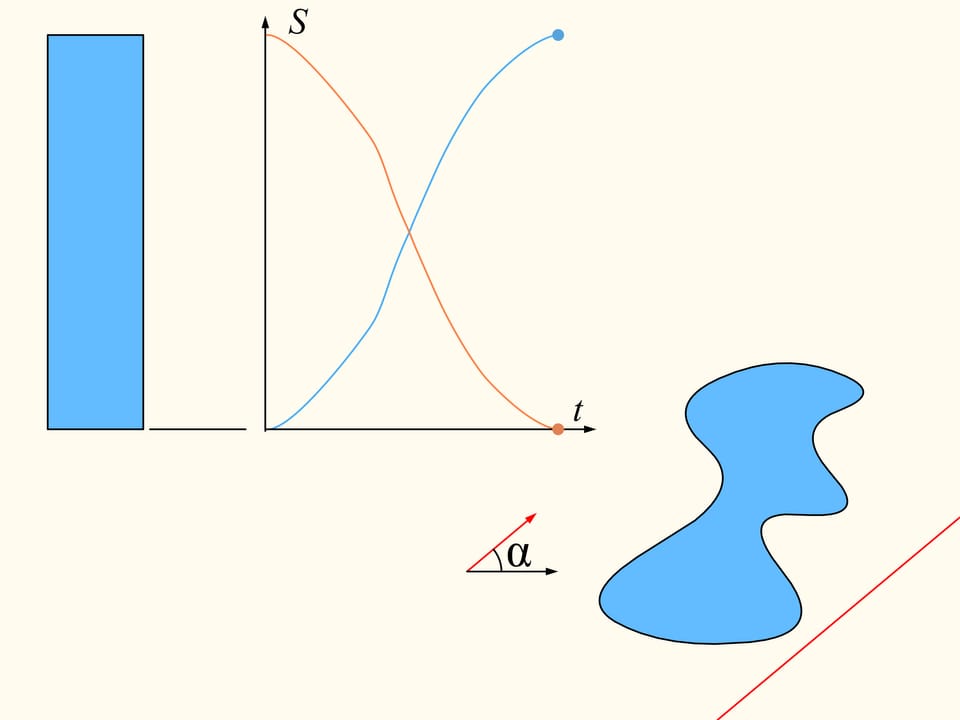
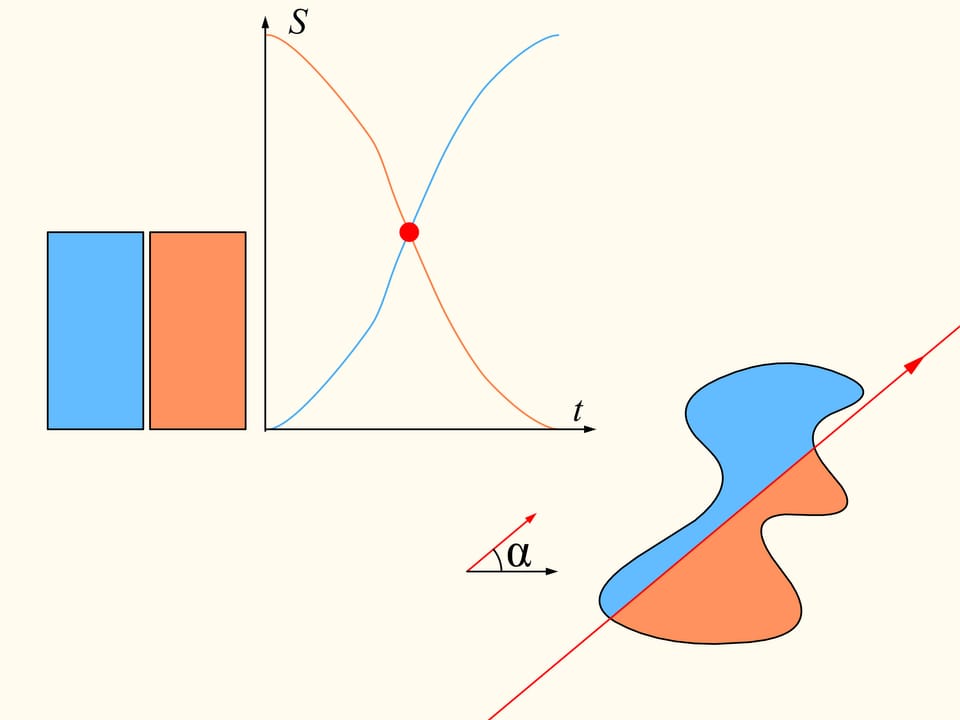
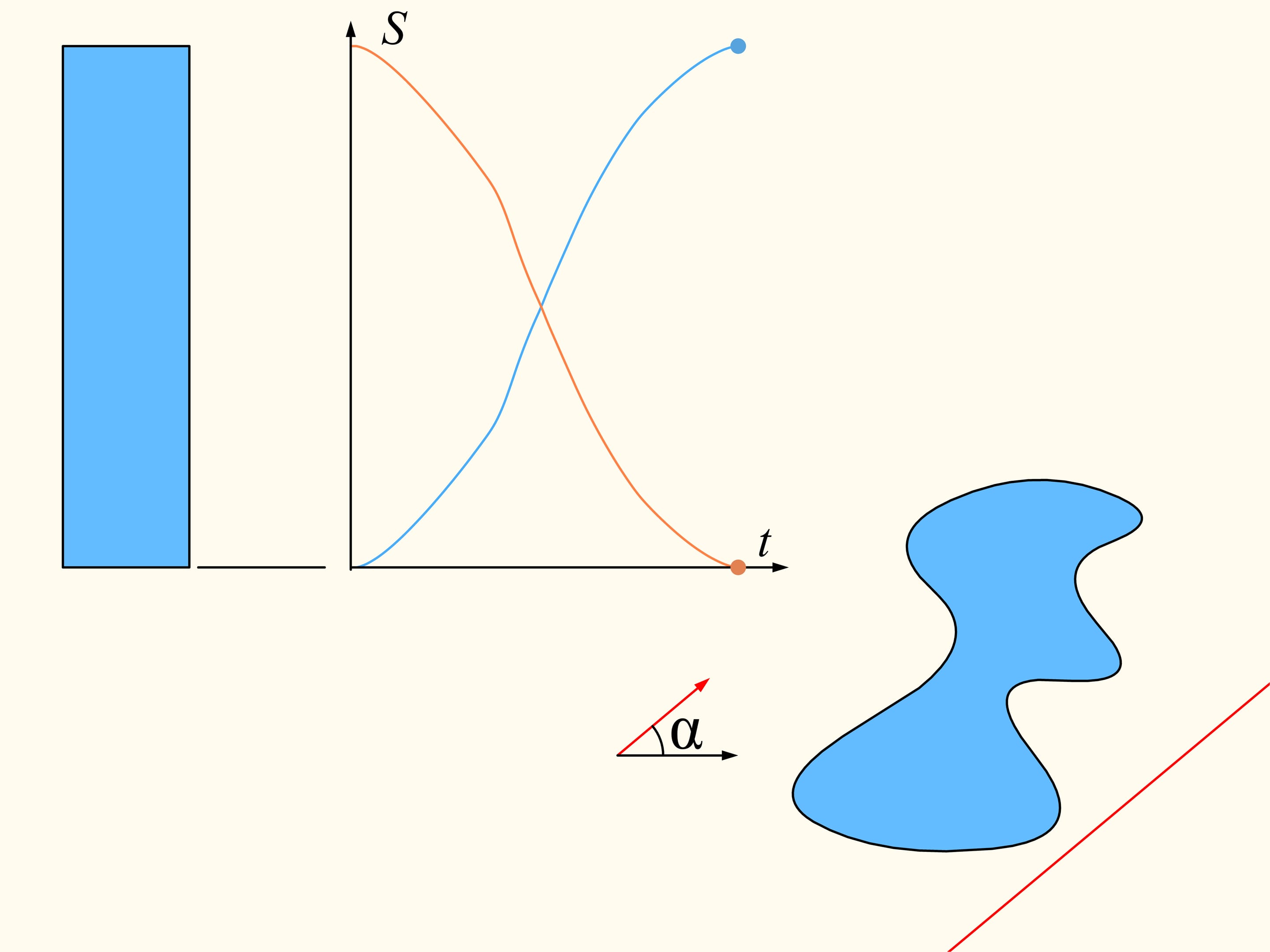
Посмотрим на полученные графики площадей справа и слева от прямой. Так как они непрерывны, то где-то существует точка пересечения. Она и соответствует искомой прямой — делящей площадь области пополам и параллельной изначально выбранному направлению.
Так как направление выбиралось произвольное, то, значит, прямая, делящая одну область пополам, существует в любом направлении.
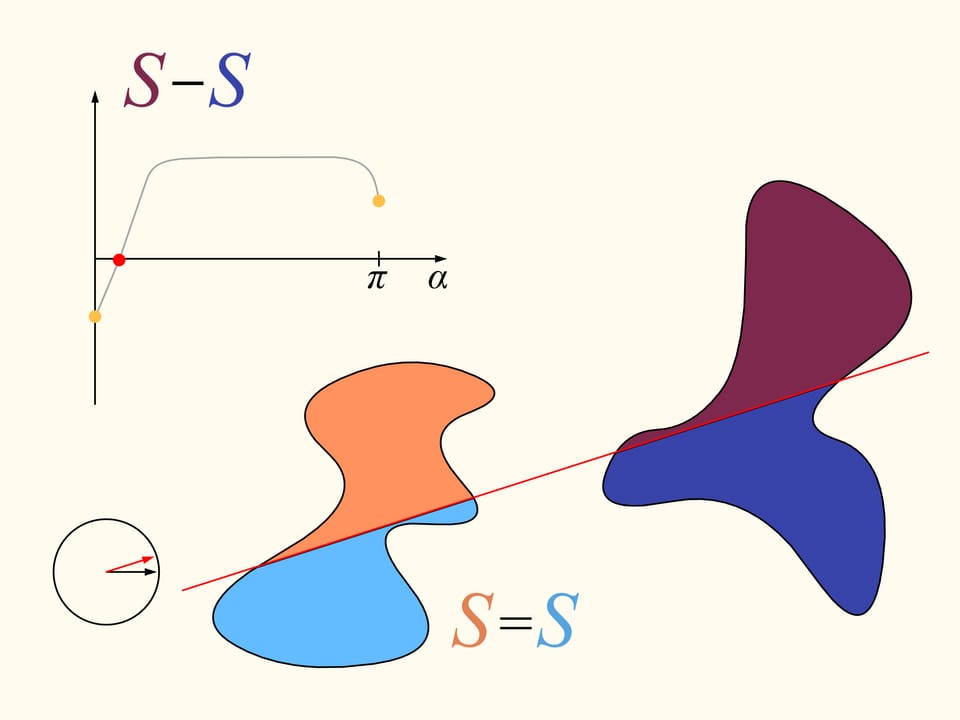
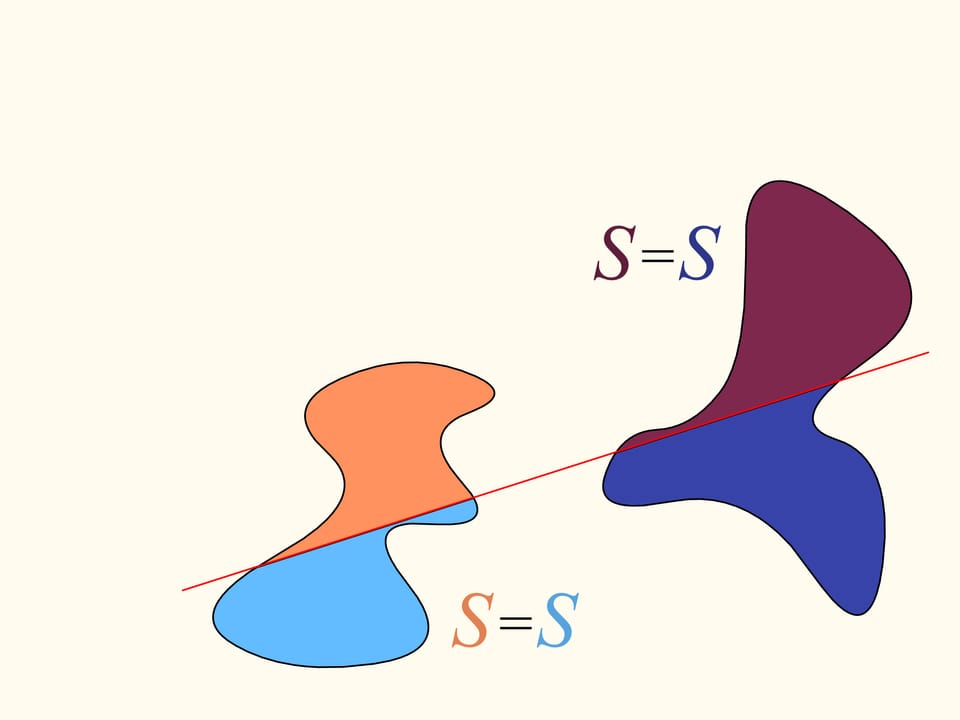
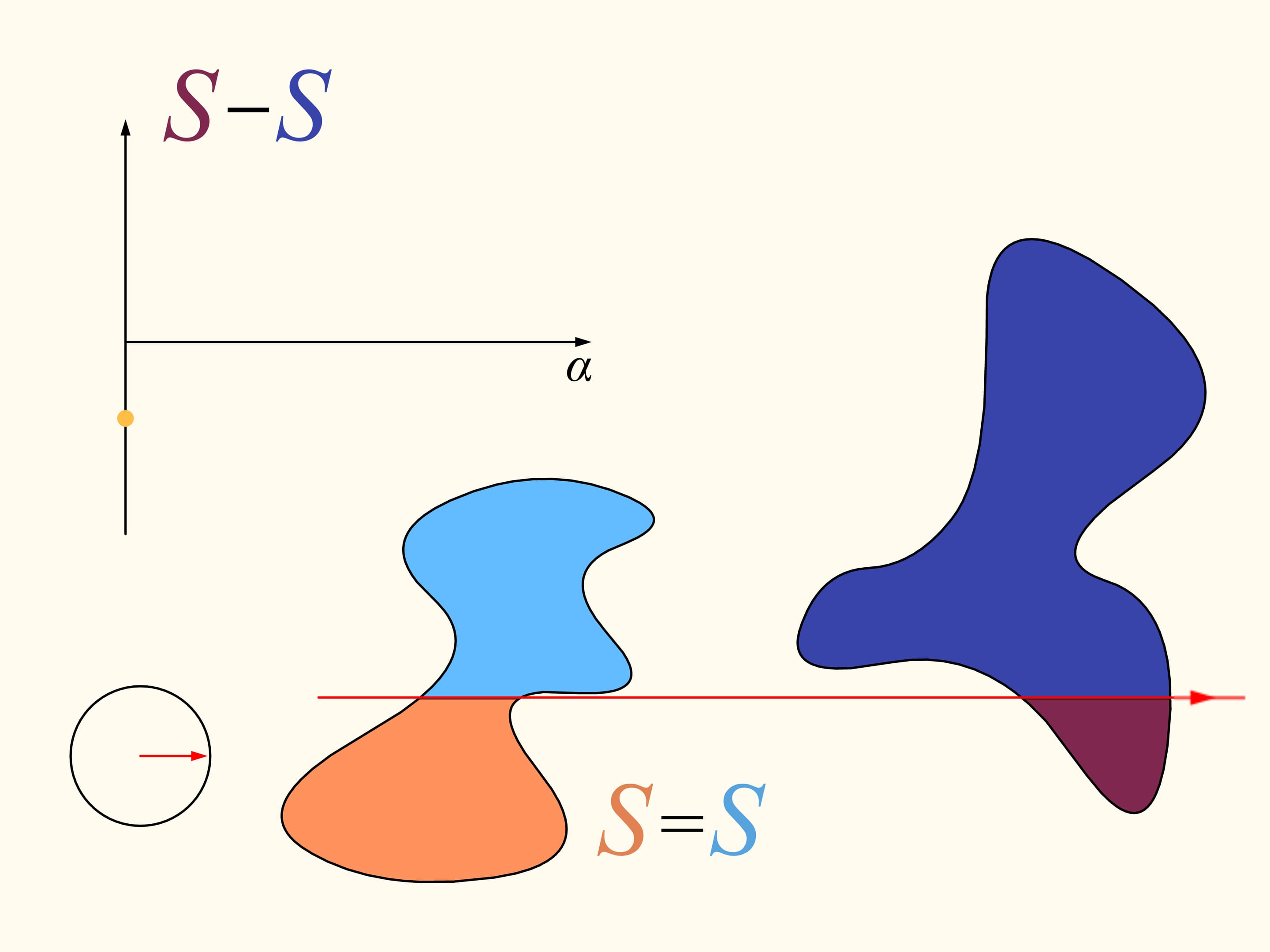
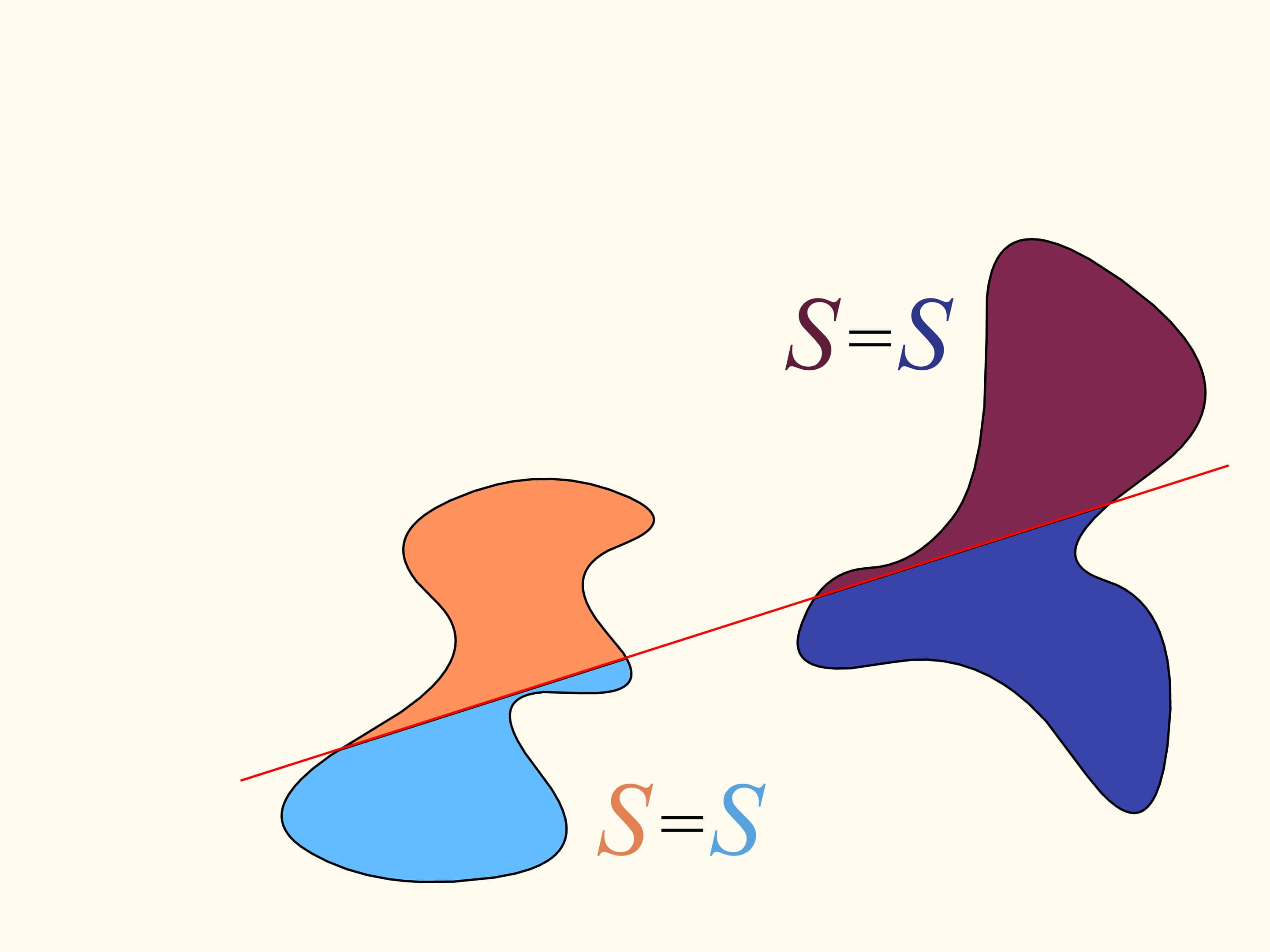
Вернёмся к двум областям. Будем рассматривать только те прямые, которые делят левую область пополам. Рассмотрим такую прямую, которая горизонтальна и направлена вправо. Она как-то поделит правую область. Будем смотреть за графиком разницы площадей правой области — площадь правее прямой минус площадь левее прямой. Сейчас эта разность отрицательна. Пробежимся по направлениям от нуля до полного угла. В этом конечном положении геометрически прямая совпадает с изначальной, а вот «право»—«лево» поменялись местами. И теперь значение рассматриваемой разности положительно. Так как разность менялась непрерывно, то, значит, её график где-то пересёк нулевое значение. И этому значению соответствует прямая, делящая правую область ровно пополам. Так как мы рассматривали только те прямые, которые делят пополам левую область, то, значит, мы нашли искомую прямую. Она делит и левую, и правую области одновременно пополам по площади.
Вот так используется теорема Больцано—Коши. К сожалению, она неконструктивна. И как проходит эта прямая в зависимости от рассматриваемых областей, без привлечения каких-то дополнительных идей, сказать нельзя. Но для любых областей доказано, что она существует! По типу такие теоремы ещё называют теоремами существования.
Перейдём к рассмотрению трёхмерного случая. Вместо двух областей на двумерной плоскости в трёхмерном пространстве рассмотрим три произвольных тела, произвольно расположенных друг относительно друга. Вместо площадей — объёмы. Оказывается, и в этом случае похожим рассуждением, что мы использовали для плоскости, можно доказать подобную теорему существования. Для любых трёх тел существует плоскость, которая каждое из тел делит по объёму ровно пополам.
Чтобы жизнь была вкуснее, рассмотрим бутерброд из хлеба, сыра и колбасы. Три тела, как-то расположенных друг относительно друга. Попробуйте доказать, что существует плоскость, делящая и колбасу ровно пополам, и одновременно сыр и хлеб тоже ровно пополам. С привлечением дополнительных рассуждений, для бутерброда, представленного в фильме, такая плоскость была найдена и, действительно, после проверки видно, что все три тела поделены ровно пополам!