Кусочно гладкое вложение многогранника⁠

Можно ли раз­вёртку многогран­ника свер­нуть в замкну­тое тело, гра­ницы кото­рого будут состо­ять не из кусоч­ков плос­ко­стей, а из кусоч­ков глад­ких поверх­но­стей?

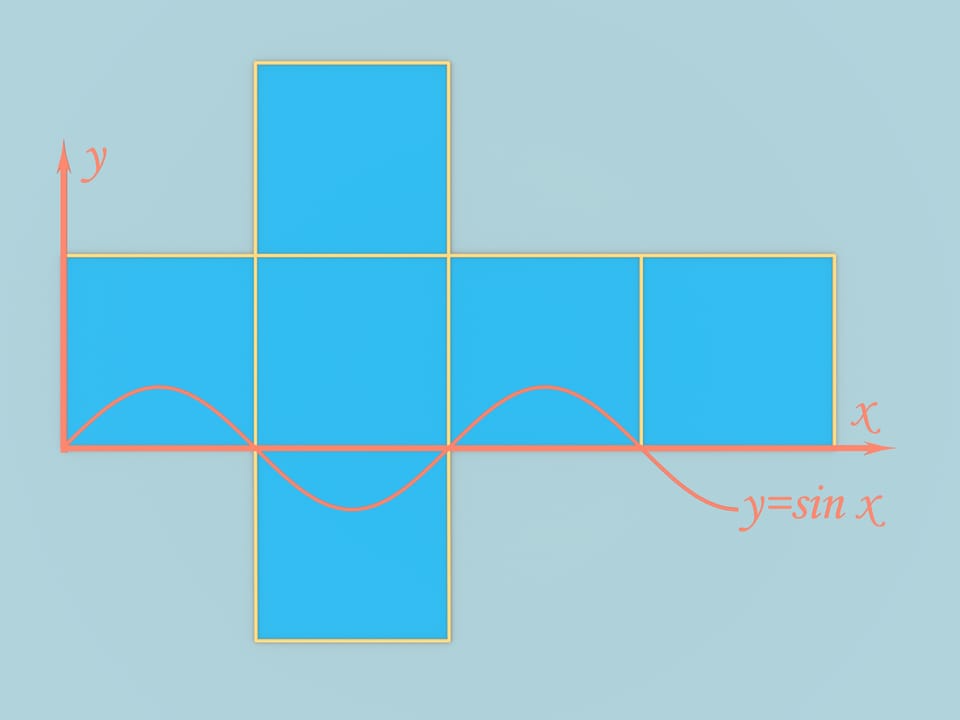
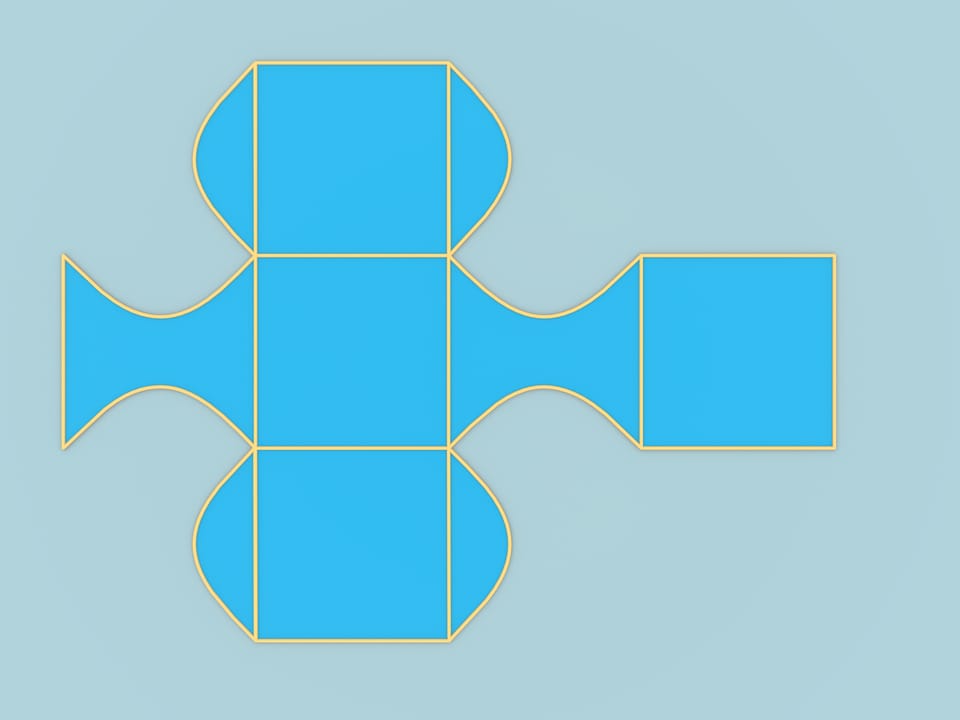
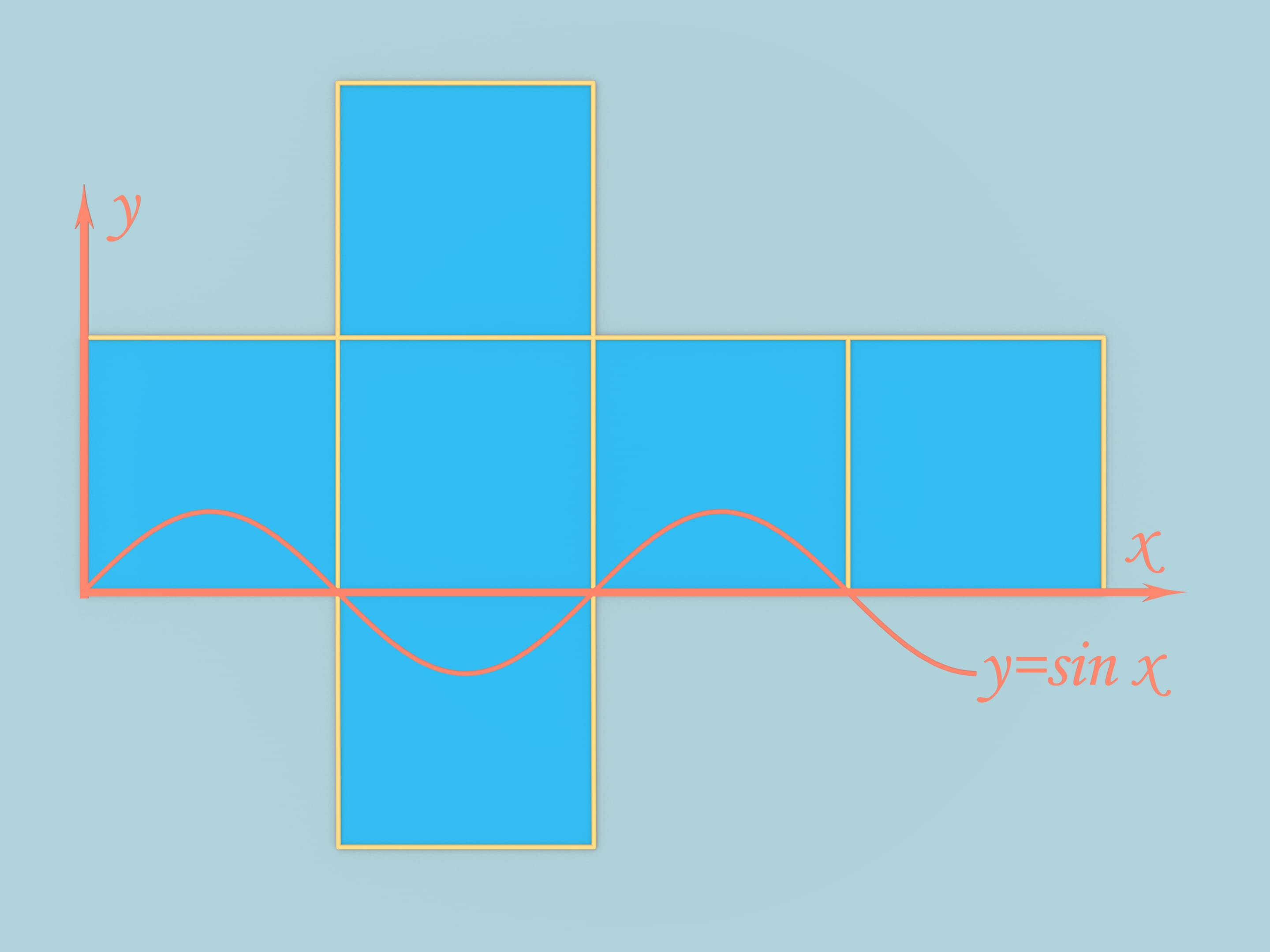
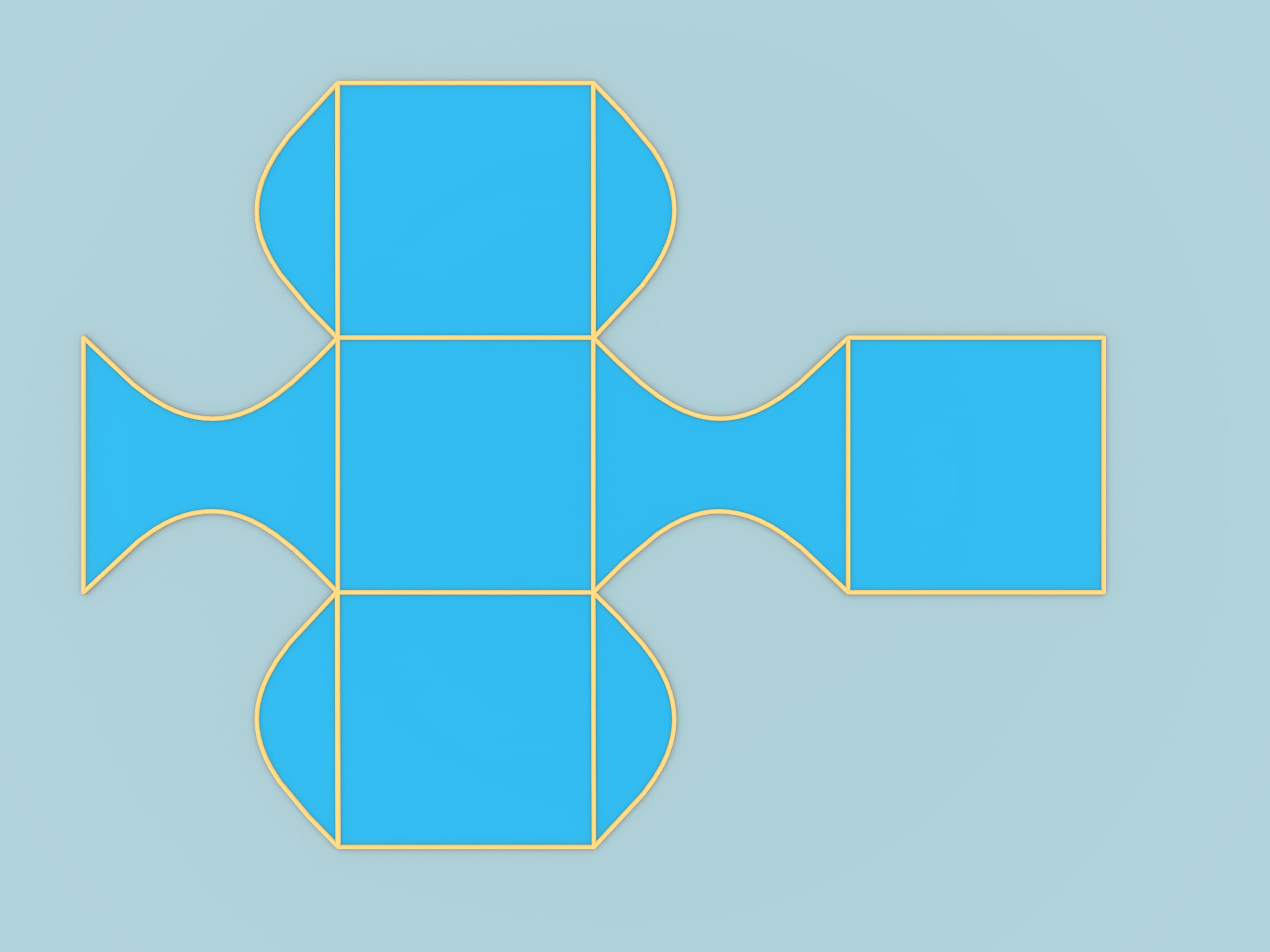
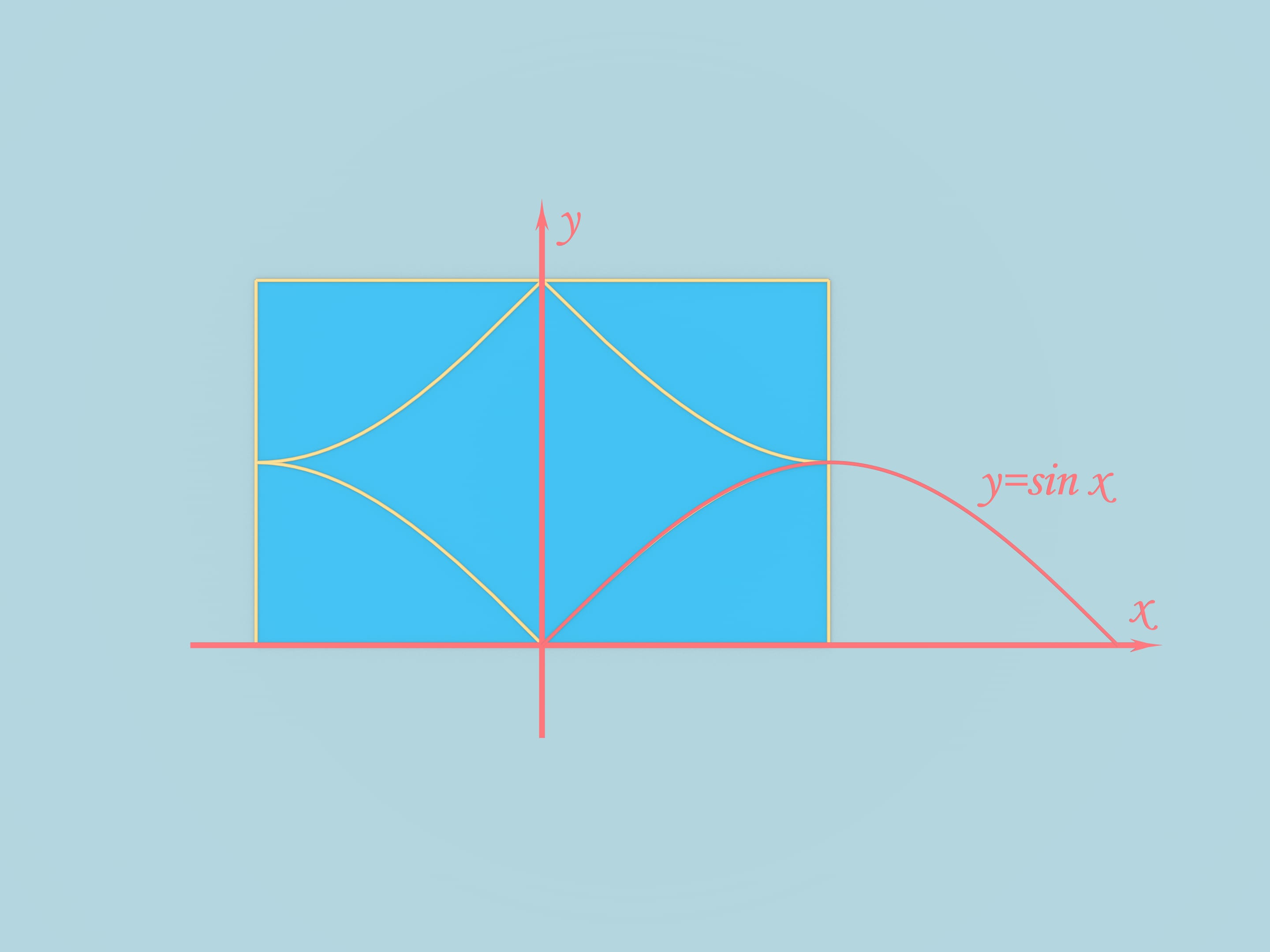
Возьмём куб с дли­ной рёбра, рав­ной $\pi$. Раз­вер­нем его в клас­си­че­скую кре­сто­об­раз­ную раз­вёртку и, спе­ци­аль­ным обра­зом про­ведя оси коор­ди­нат, нари­суем функцию $y = \sin (x)$. Пере­ложим кусочки раз­вёртки, отсе­ка­емые сину­со­и­дой, и симмет­рич­ные им. Раз­вёртка не изме­ни­лась, так как усло­вия склейки гра­ниц при пере­кла­ды­ва­нии были сохра­нены. Из полу­чен­ной фигуры можно сложить вот такое тело.

Однако рас­смот­рен­ный при­мер, хотя и отве­чает на постав­лен­ный вопрос, обла­дает одним недо­стат­ком. Его гра­ница содержит два куска, уна­сле­до­ван­ных от куба, кото­рые являются кусоч­ками плос­ко­стей. После постро­е­ния этого при­мера кон­струкция, не обла­дающая ука­зан­ным мину­сом, воз­никла очень быстро.

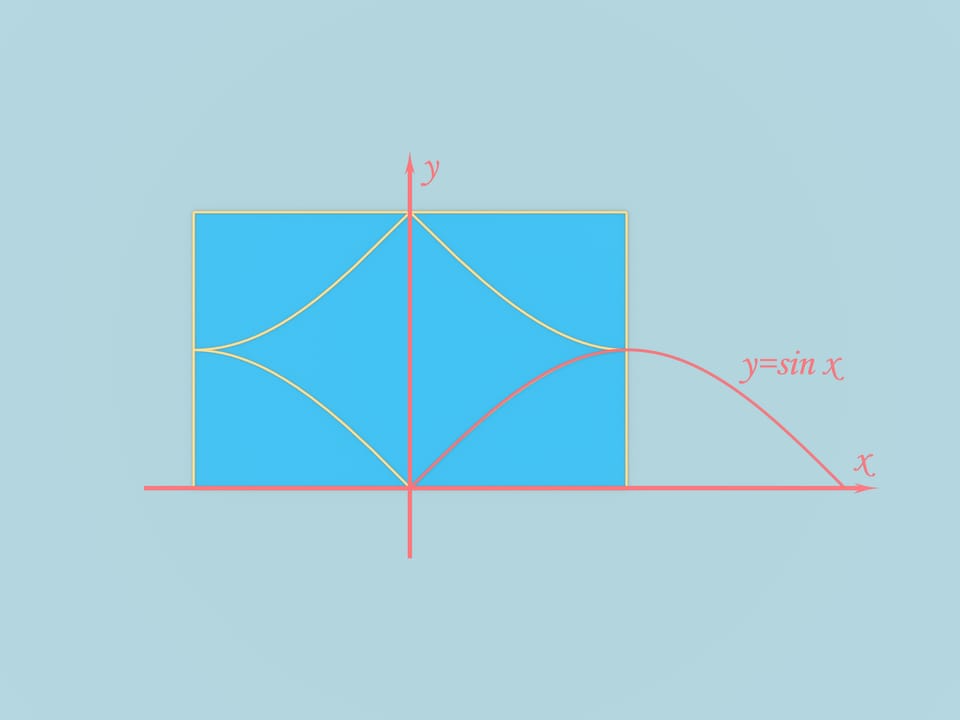
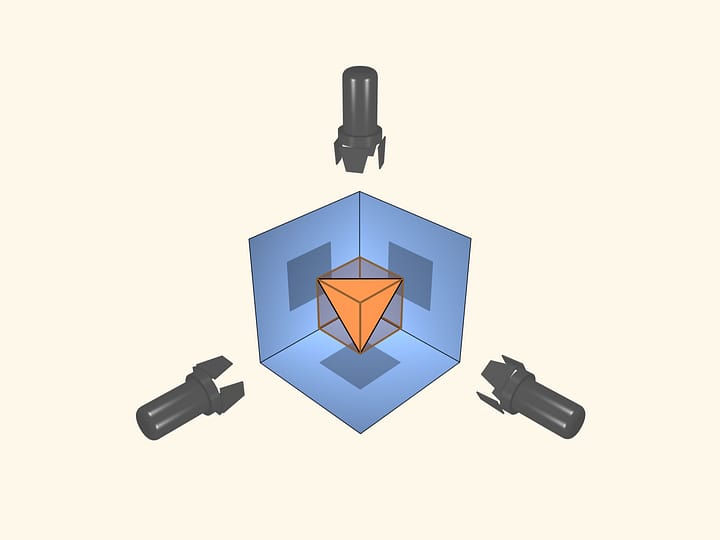
Возьмём прямо­уголь­ный лист бумаги с отноше­нием сто­рон, рав­ным $\pi/2$. Из него, как из любого прямо­уголь­ного листа, можно свер­нуть тре­уголь­ную пирамиду. Для этого соеди­ним реб­рами сере­дины сосед­них сто­рон, а также про­ве­дём ребро, соеди­няющее сере­дины длин­ных сто­рон. Скла­ды­вая по этим рёб­рам, полу­чим тре­уголь­ную пирамиду.

Из этого же листа бумаги можно полу­чить и другую фигуру, гра­ница кото­рой будет состав­лена из глад­ких поверх­но­стей. Соеди­ним сере­дины сосед­них сто­рон «чет­вер­тин­ками» сину­соид. Согнём лист по этим рёб­рам. Полу­чим вот такое кра­си­вое тело. Оно явля­ется пере­се­че­нием трёх цилин­дров: двух касающихся и одного направ­лен­ного в перпен­ди­ку­ляр­ном направ­ле­нии. Таким обра­зом, гра­ница фигуры состоит из трёх кусоч­ков цилин­дров.

Уди­ви­тельно, насколько юна матема­тика. Каза­лось бы, такие при­меры должны были быть постро­ены если и не во времена Архимеда, то всё равно очень давно. Однако при­меры, кото­рые мы рас­смот­рели, были постро­ены только осе­нью 2004 года.