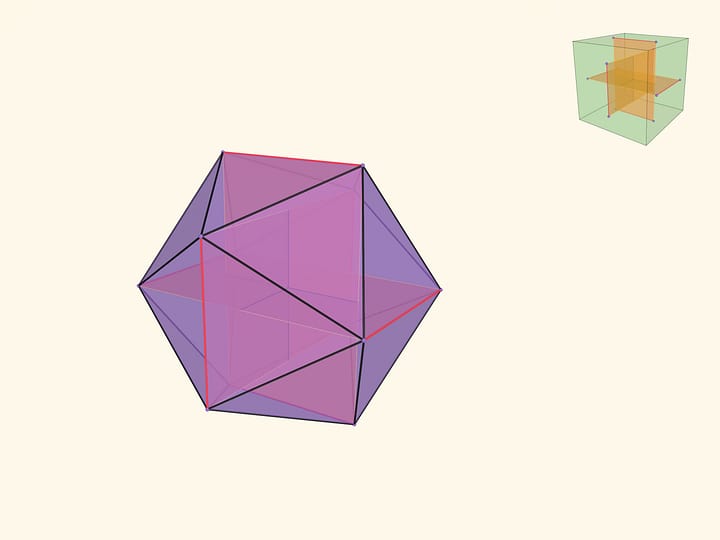
Можно ли из одинаковых граней сложить выпуклый и невыпуклый многогранники? Конечно, можно, скажете вы. Один из примеров приведён на этом рисунке.
Многогранник называется выпуклым, если он лежит по одну сторону от плоскости, содержащей любую из его граней.
Многогранник называется невыпуклым, если у него существует такая грань, что многогранник оказывается по обе стороны от плоскости, содержащей эту грань.
Пусть из одинаковых наборов граней удалось сложить выпуклый и невыпуклый многогранник. У которого из них объём будет больше?
Оказывается можно так подобрать грани, что объём невыпуклого многогранника будет больше объёма выпуклого, составленного из тех же граней. В фильме рассказывается о наилучшем известном таком примере.
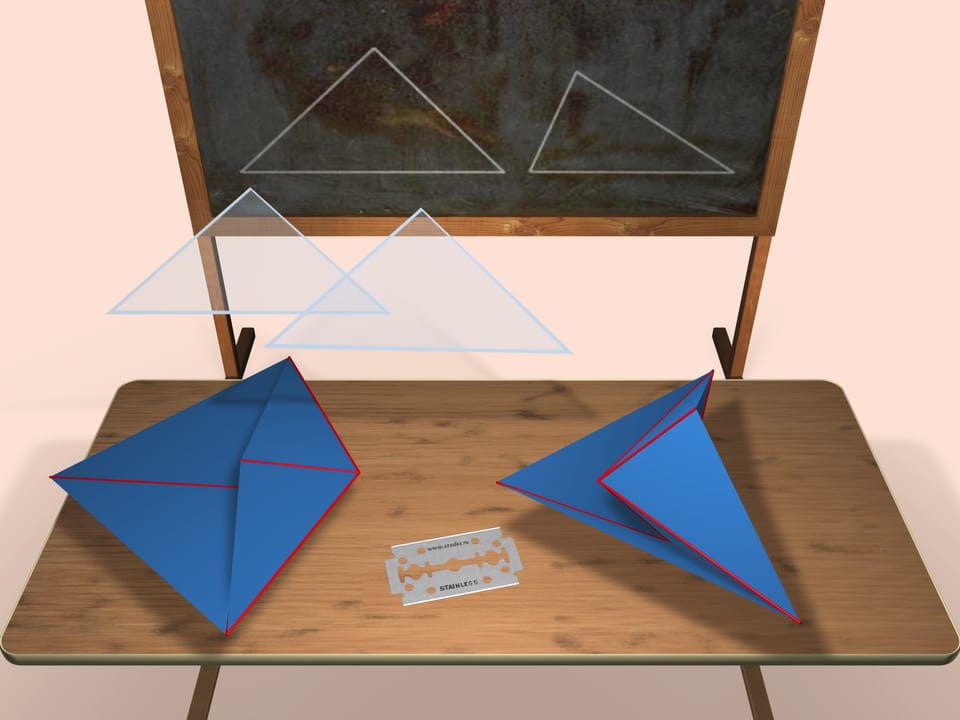
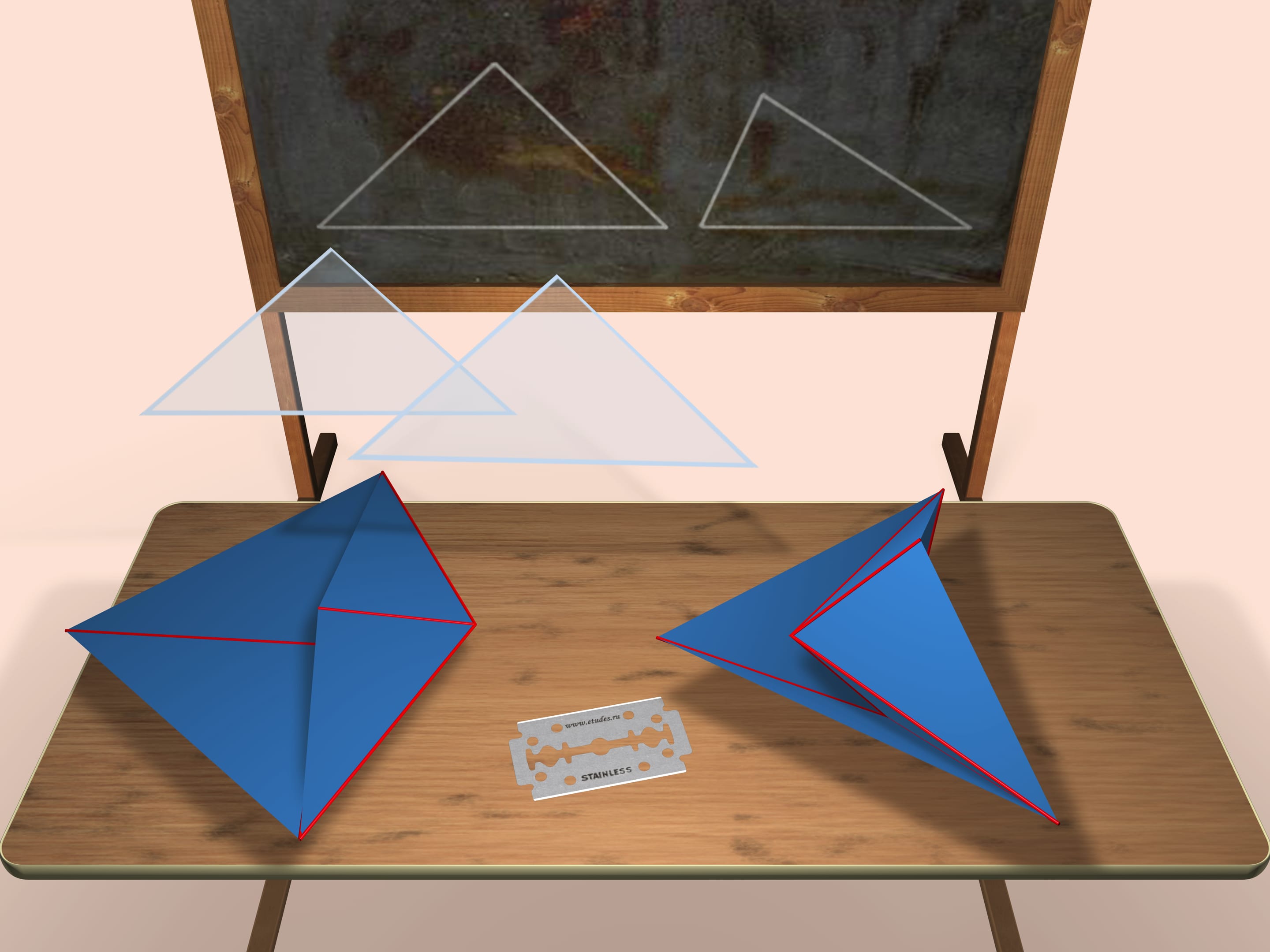
Рассмотрим два треугольника (точные длины сторон будут указаны в конце фильма), которые и будут гранями будущих многогранников. Как мы видим, каждый треугольник одновременно становится гранью и в одном, и в другом многограннике. Тот многогранник, который строится слева, будет выпуклым, тот, что справа — невыпуклым.
Оба построенных многогранника — октаэдры (хотя и не правильные), т. е. имеют по шесть вершин и восемь граней.
Что такое в житейском смысле объём тела, в частности многогранника? Это то, сколько жидкости может быть налито внутрь этого многогранника. Отрежем вершинки и нальём внутрь каждого многогранника воду. Выпуклый многогранник уже наполнился, а невыпуклый — ещё нет. Но, возможно, вода наливалась с разной скоростью: чтобы правильно сравнить объёмы, выльем жидкость из каждого многогранника в одинаковые стаканы. Уровень воды в правом стакане выше, чем в левом, значит, объём невыпуклого многогранника действительно больше объёма выпуклого.
Если посчитать аккуратно, то можно вычислить, что отношение объёма невыпуклого многогранника к объёму выпуклого равно 1,163.
В нашей задаче действительно правильнее рассматривать отношение объёмов, а не их разницу, так как отношение не зависит от размеров изначальных треугольников, использованных в качестве граней для построения многогранников.
В рассмотренном примере объём построенного невыпуклого многогранника более чем на 16% больше объёма выпуклого. Данные многогранники вы можете реализовать сами, используя грани с указанными сторонами. При этом, если центры октаэдров расположить в начале координат, то, с точностью до поворота, координаты вершин будут такие, как приведены в фильме.
В фильме рассмотрен пример построения двух многогранников, предложенный С. Н. Михалёвым в 2002 году, в то время аспирантом механико-математического факультета МГУ. Это лучший из известных примеров (с максимальным известным отношением объёмов многогранников).
Однако до сих пор неизвестно, насколько большим может быть отношение объёма невыпуклого многогранника к объёму выпуклого, составленного из тех же граней. Этот вопрос ещё ждёт своего исследователя!
Литература
Болтянский В. Г., Яглом И. М. Выпуклые фигуры. — М.—Л., ГТТИ, 1951. — (Библиотека математического кружка; Вып. 4).
Михалёв С. Н. Изометрические реализации октаэдров Брикара 1-го и 2-го типов с известными значениями объёма // Фундаментальная и прикладная математика. — 2002. — Т. 8, № 3. — Стр. 755—768.