Главной характеристикой вершины выпуклого многогранника является «угловой дефект» в этой точке.
Окружность небольшого радиуса с центром в точке на грани многогранника будет иметь длину $2\pi r$, а круг, ограничиваемый этой окружностью, будет прилегать к поверхности.
Даже если круг сдвинуть так, чтобы он свешивался через ребро, он будет прилегать к поверхности многогранника.
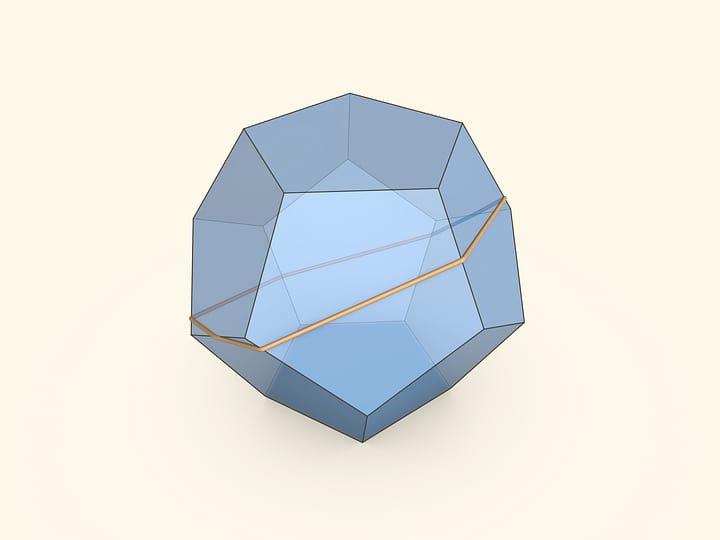
Но если в качестве центра круга взять вершину выпуклого многогранника, то невозможно приложить круг к поверхности многогранника без складок. Окружность — множество всех точек поверхности выпуклого многогранника, одинаково удалённых от его вершины, имеет меньшую длину, чем окружность на плоскости.
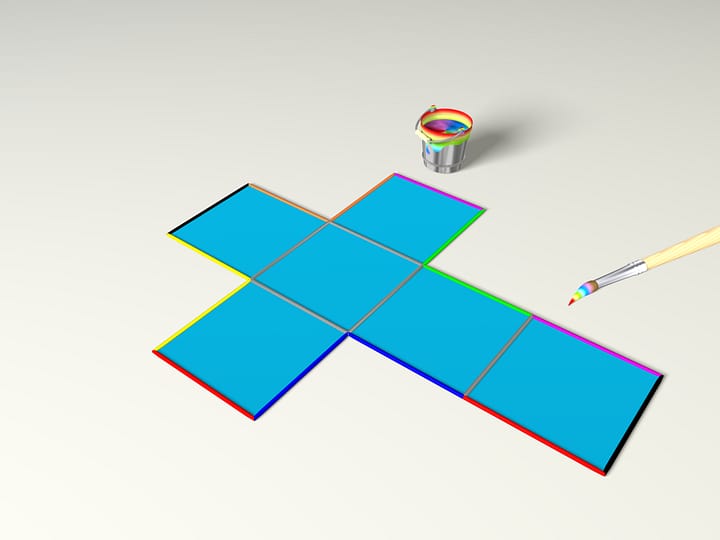
Если посчитать сумму угловых дефектов по всем вершинам представленного в фильме куба, то получится $4\pi$. Оказывается, что и для любого выпуклого многогранника сумма угловых дефектов по вершинам равна $4\pi$. Этот факт является одним из проявлений формулы Эйлера.
Для заинтересованных читателей приведём доказательство этого факта. Триангулируем поверхность выпуклого многогранника: все грани разобьём на треугольники. Пусть треугольников получилось $F$ штук и у них $V$ вершин.
Посчитаем сумму всех углов всех треугольников. С одной стороны, при подсчёте по треугольникам, она равна $F\cdot\pi$. С другой стороны, так как количество вершин в триангуляции равно $V$, то эта же сумма равна $V\cdot 2π-d$, где $d$ — сумма угловых дефектов по всем вершинам многогранника. Приравнивая, получаем: $d=(V-F/2)\cdot 2\pi$.
Так как в триангуляции к каждой стороне примыкает по два треугольника, а каждый треугольник, как ни странно, имеет по три стороны, то $3F=2E$, где $E$ — количество рёбер в триангуляции, т.е. $\frac{3}{2}F=E$, или $F/2=E-F$. А значит, $V-F/2=V-E+F=2$ по формуле Эйлера, так как многогранник выпуклый. Тем самым, сумма дефектов выпуклого многогранника действительно равна $4\pi$.
Последний шаг — применение формулы Эйлера — подсказывает, чему будет равна сумма дефектов и для невыпуклых многогранников. Например, если многогранник топологически представляет собой тор, то сумма дефектов равна $0$.
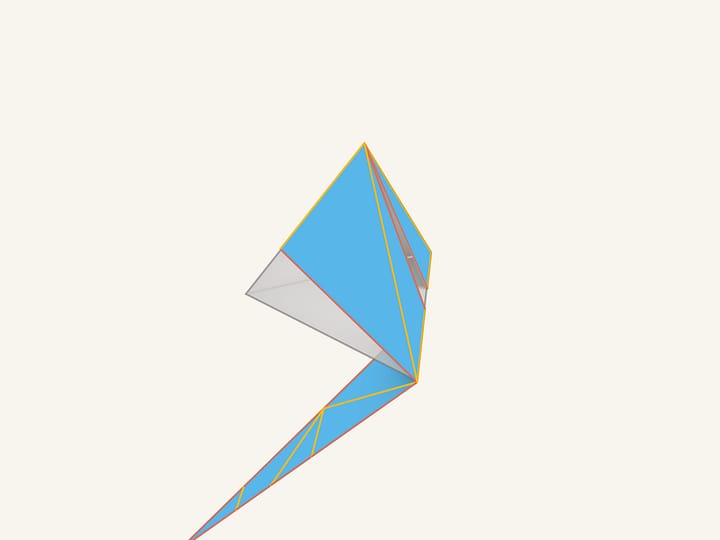
Угловой дефект — характеристика вершин выпуклого многогранника. В определённом смысле верно и обратное: это характеристика вершин выпуклого многогранника не только когда он представлен в виде многогранника, но и для его представления в виде развёртки. Напомним, что в понятие развёртки входит не только сам «кусок бумаги», но и условия склейки границ. А значит, определены вершины — точки, в которых есть угловой дефект. Теорема А. Д. Александрова утверждает, что из любой развёртки, у которой в каждой вершине дефект неотрицательный, а суммарный дефект равен $4\pi$, можно сложить выпуклый многогранник.
Литература
Долбилин Н. П. Жемчужины теории многогранников. — М. : МЦНМО, 2000.