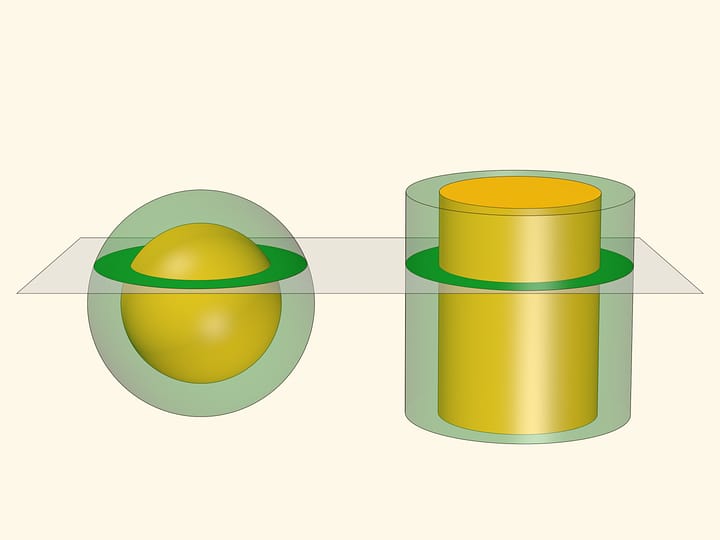
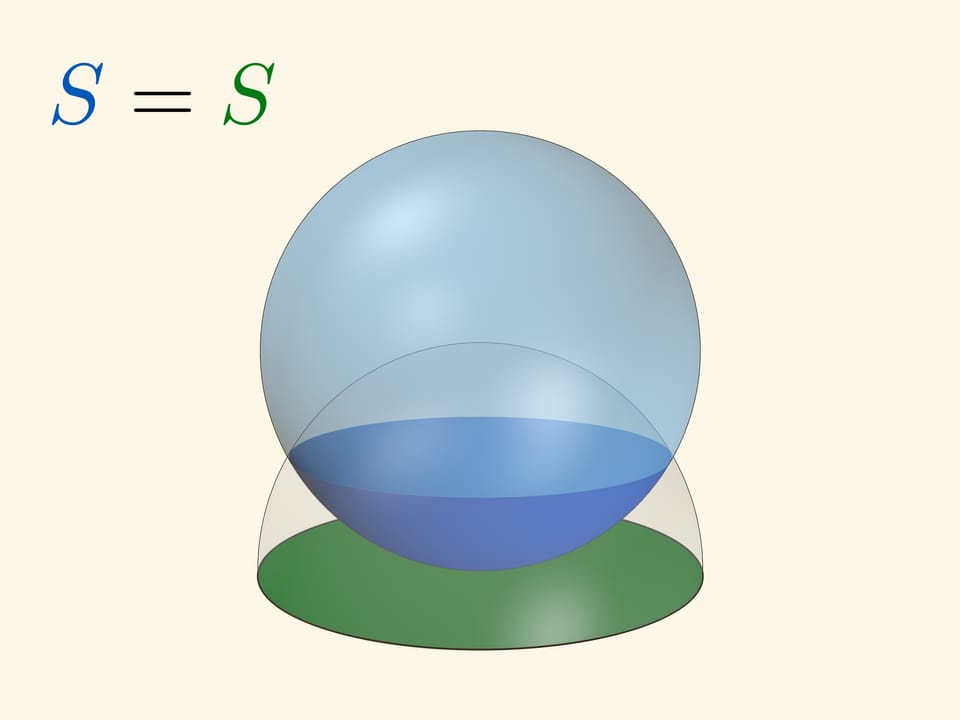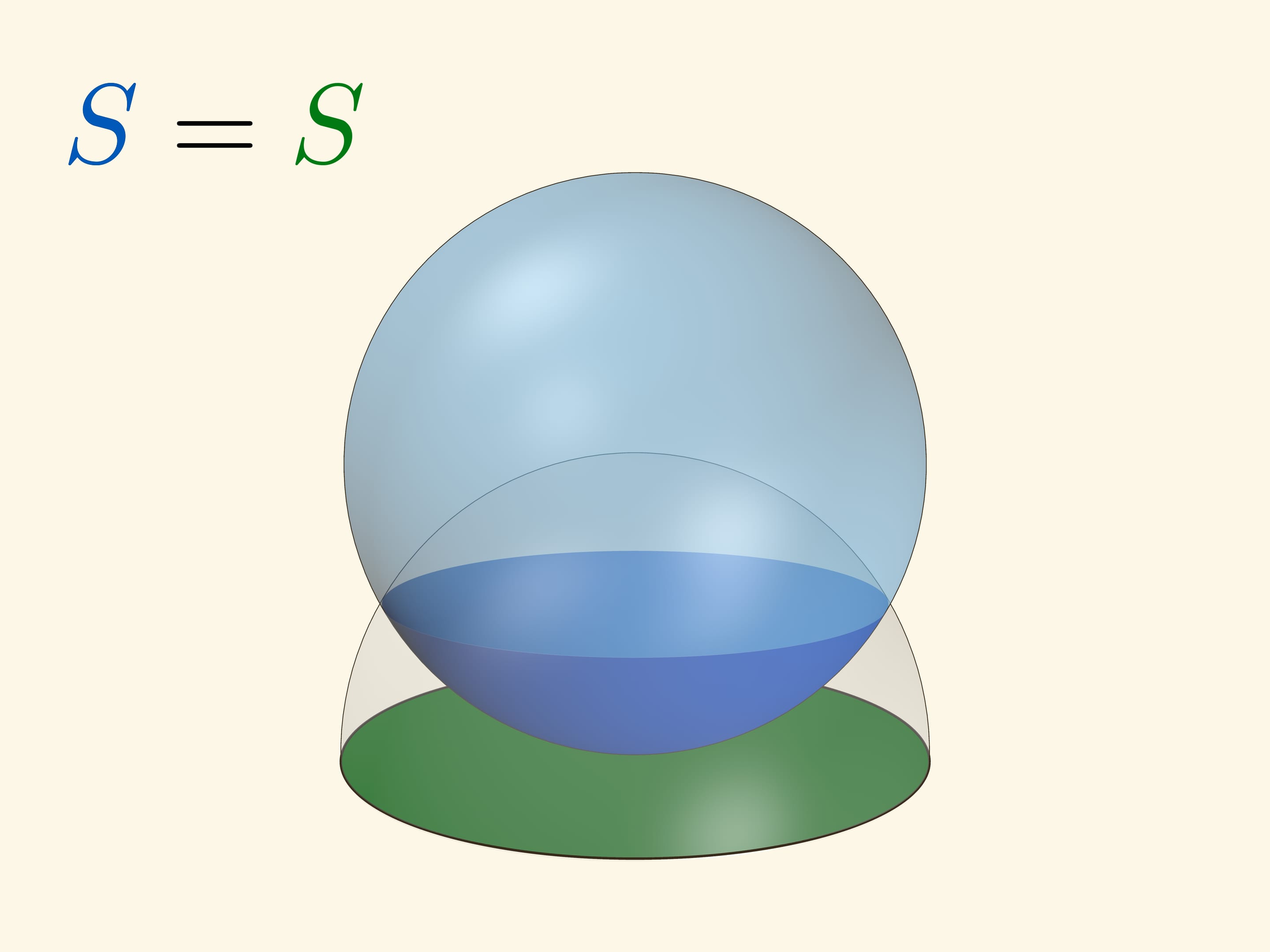Площадь всей сферы, шапочки или кольца на сфере посчитать не так просто. Помогает сравнение сферы с «плоскими» поверхностями — плоскостью, конусом и цилиндром.
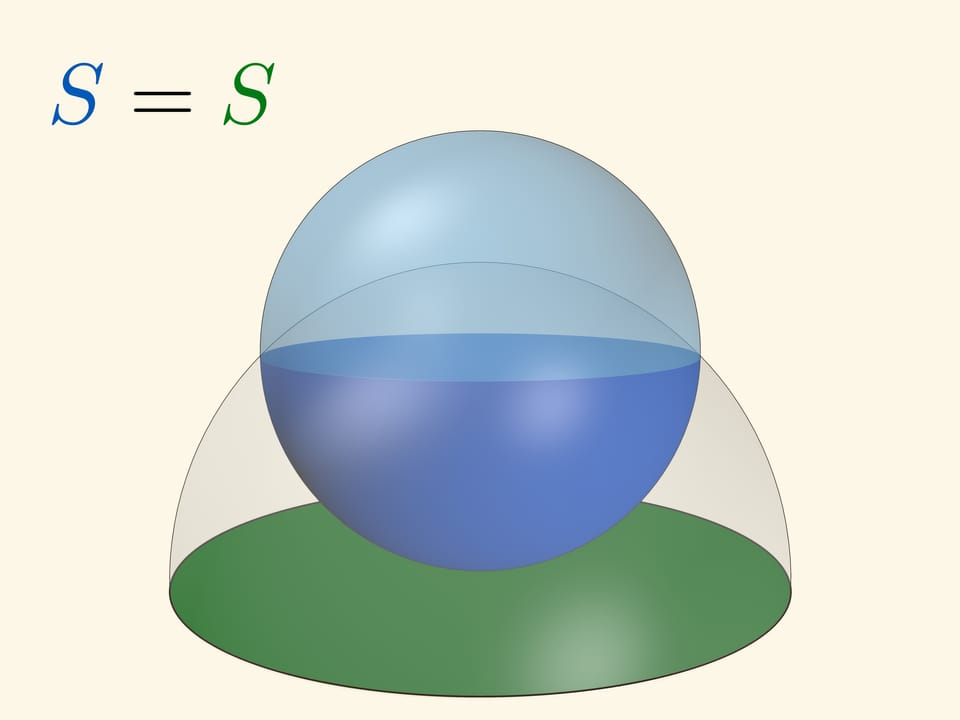
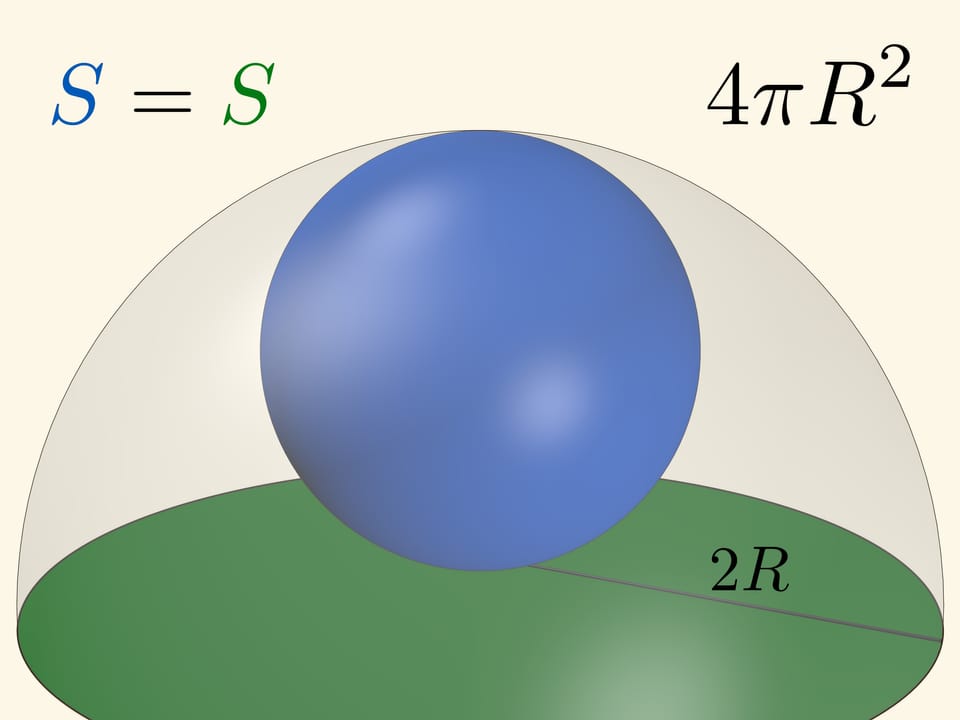
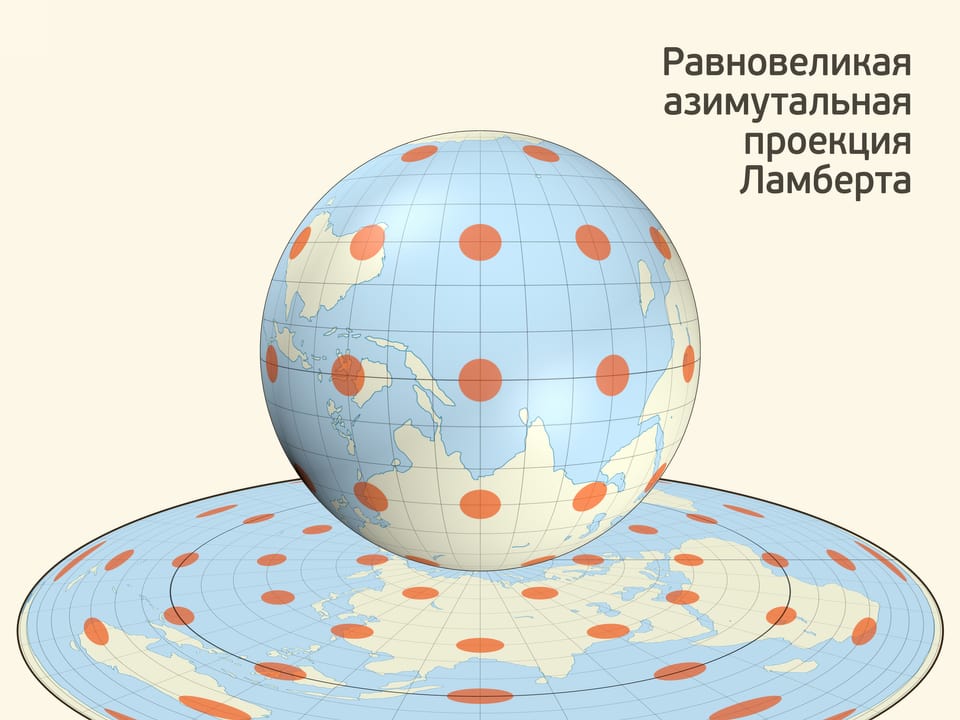
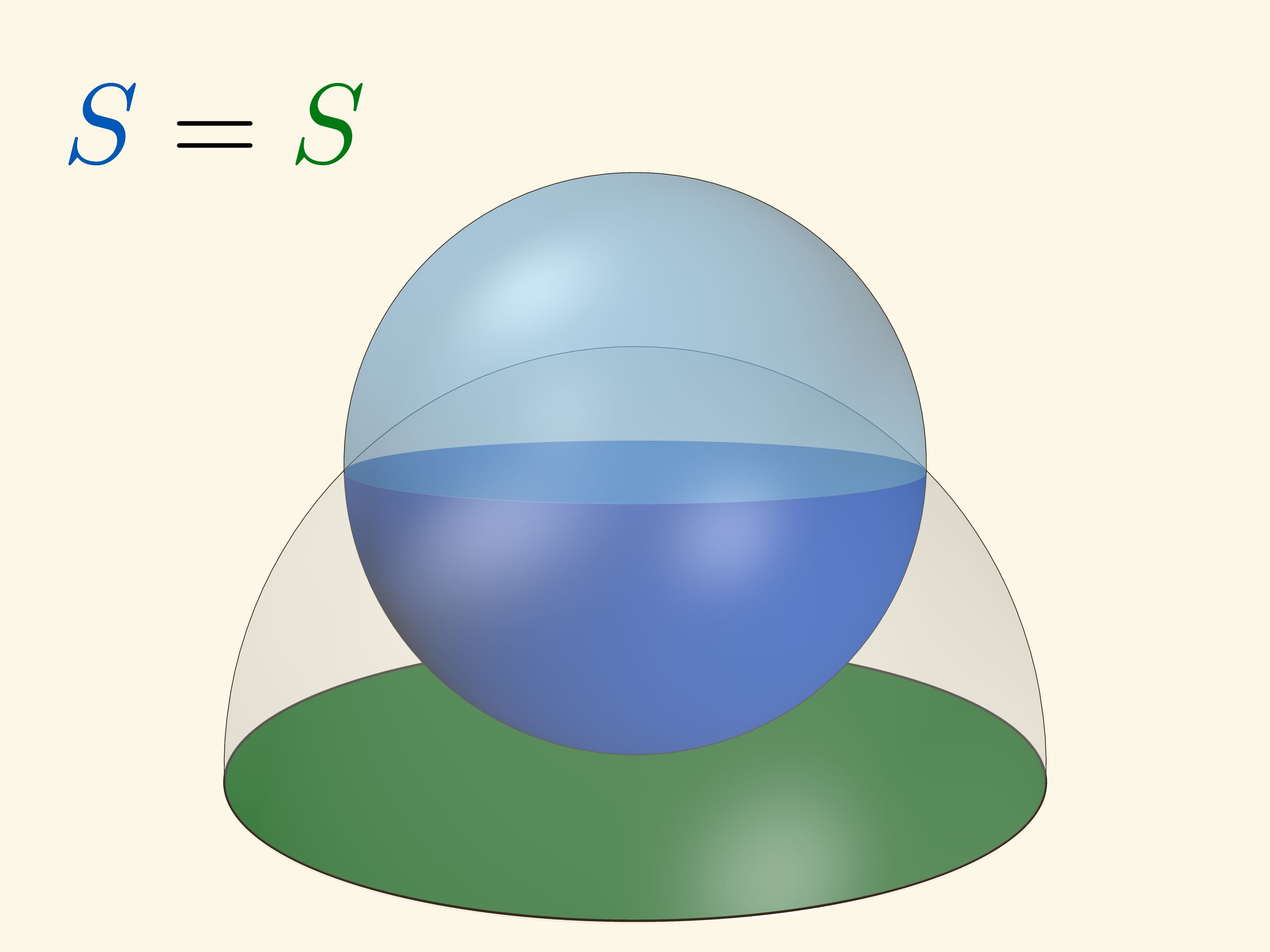
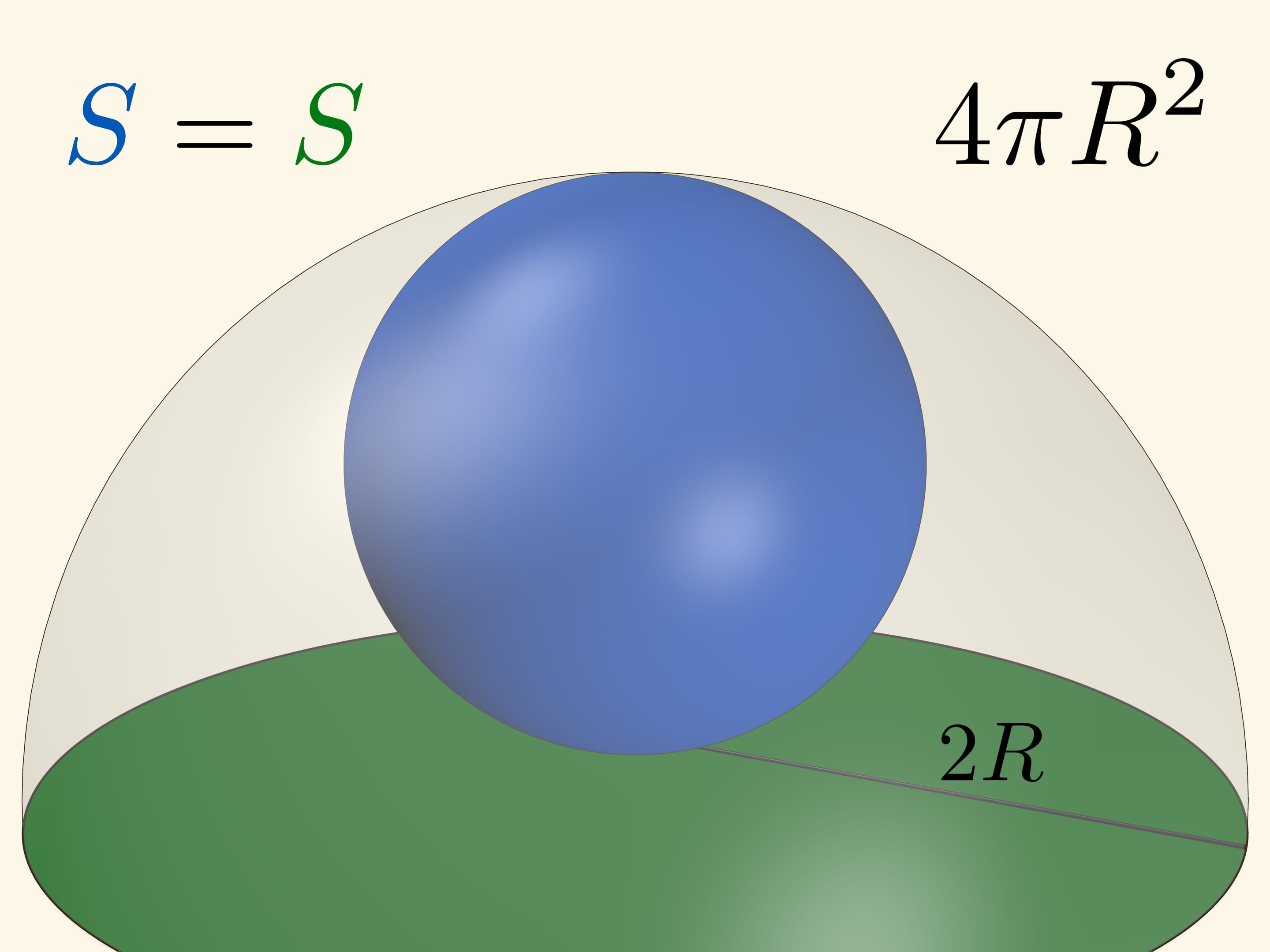
Если плоскость касается сферы в полюсе, то площадь сферической шапочки и круга на плоскости, высекаемых «вспомогательной» сферой с центром в полюсе, — одинакова. Если радиус вспомогательной сферы равен диаметру основной, то вспомогательная полностью охватывает основную сферу. Эта картинка позволяет запомнить, что площадь сферы равна $4\pi R^2$.
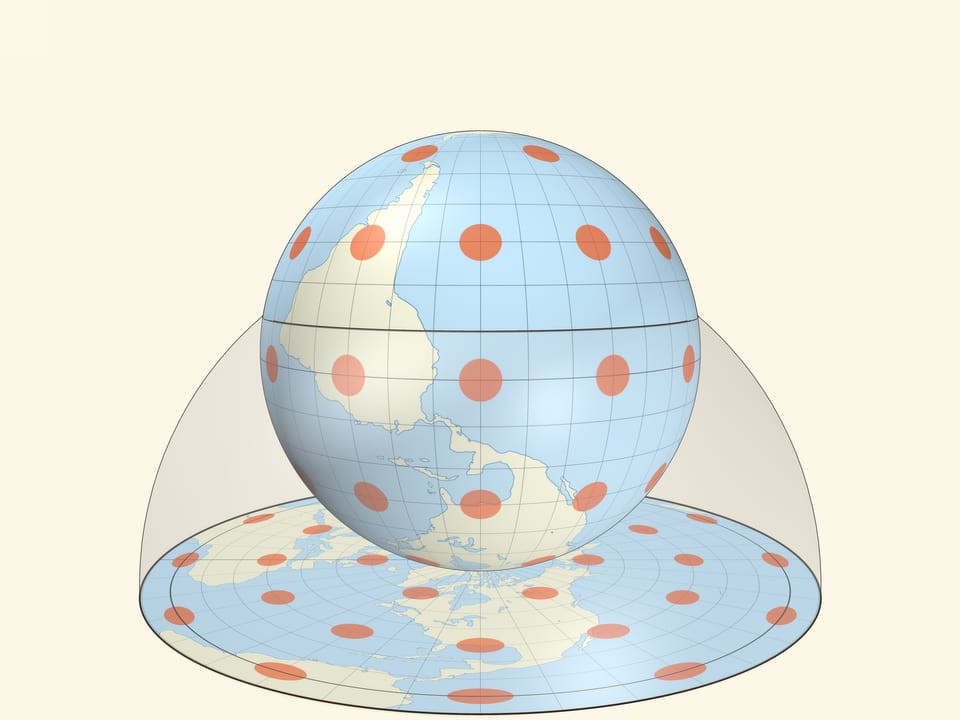
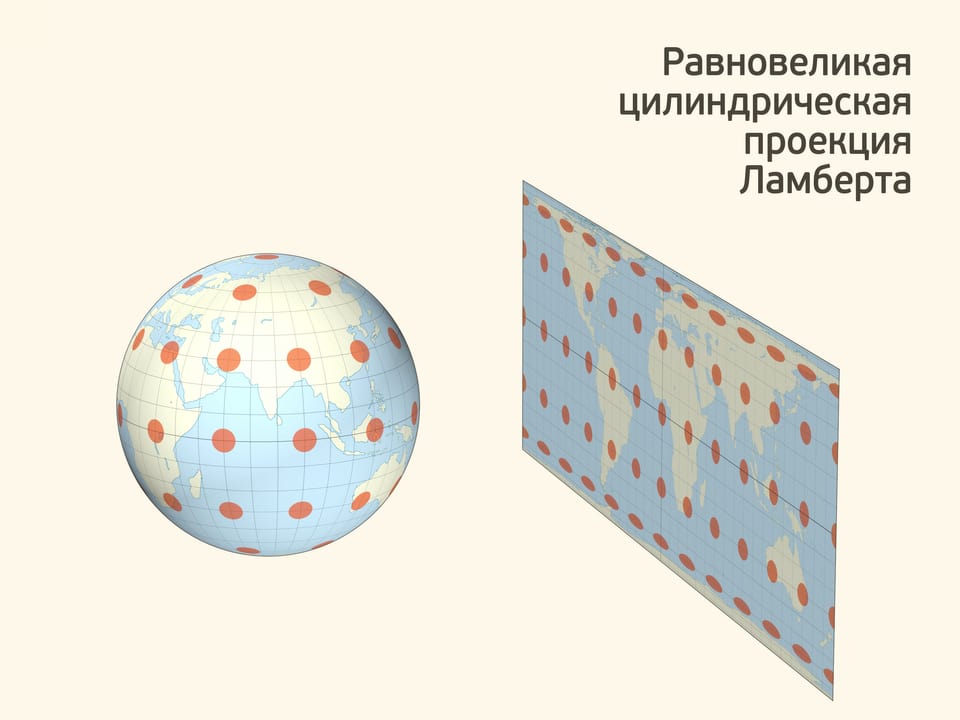
«Считывая» с глобуса информацию по приведённому алгоритму, можно построить равновеликую азимутальную картографическую проекцию Земли. Такая проекция сохраняет площади всех областей. Разработал её математик и астроном Иоганн Ламберт — тот самый, который доказал иррациональность числа $\pi$. Заметный недостаток проекции — значительное искажение на общей карте Земли контуров крупных областей, например, континентов.
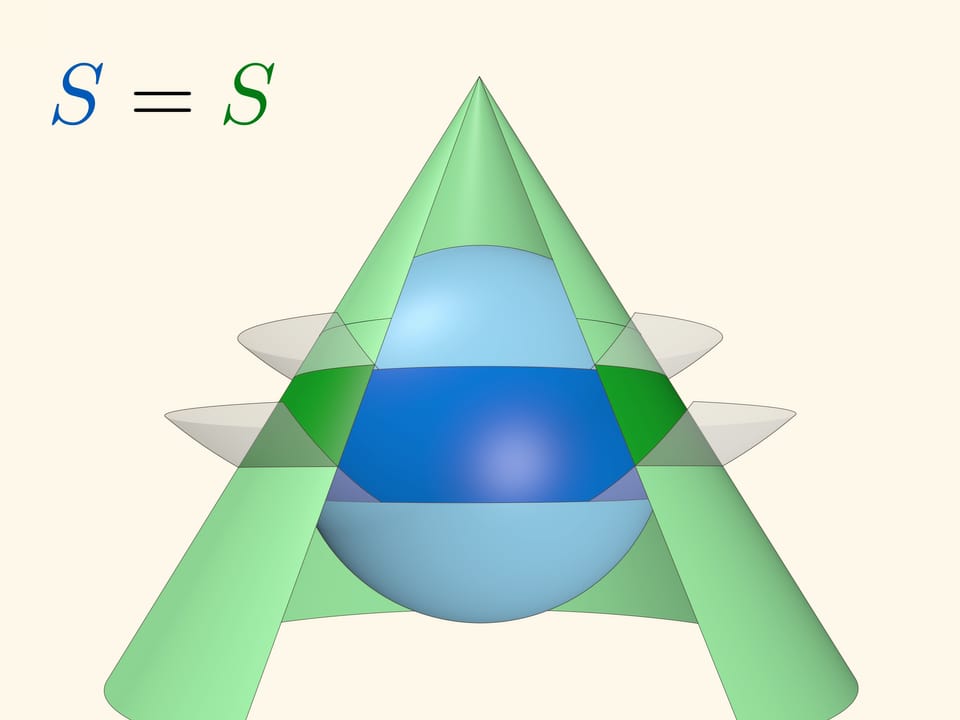
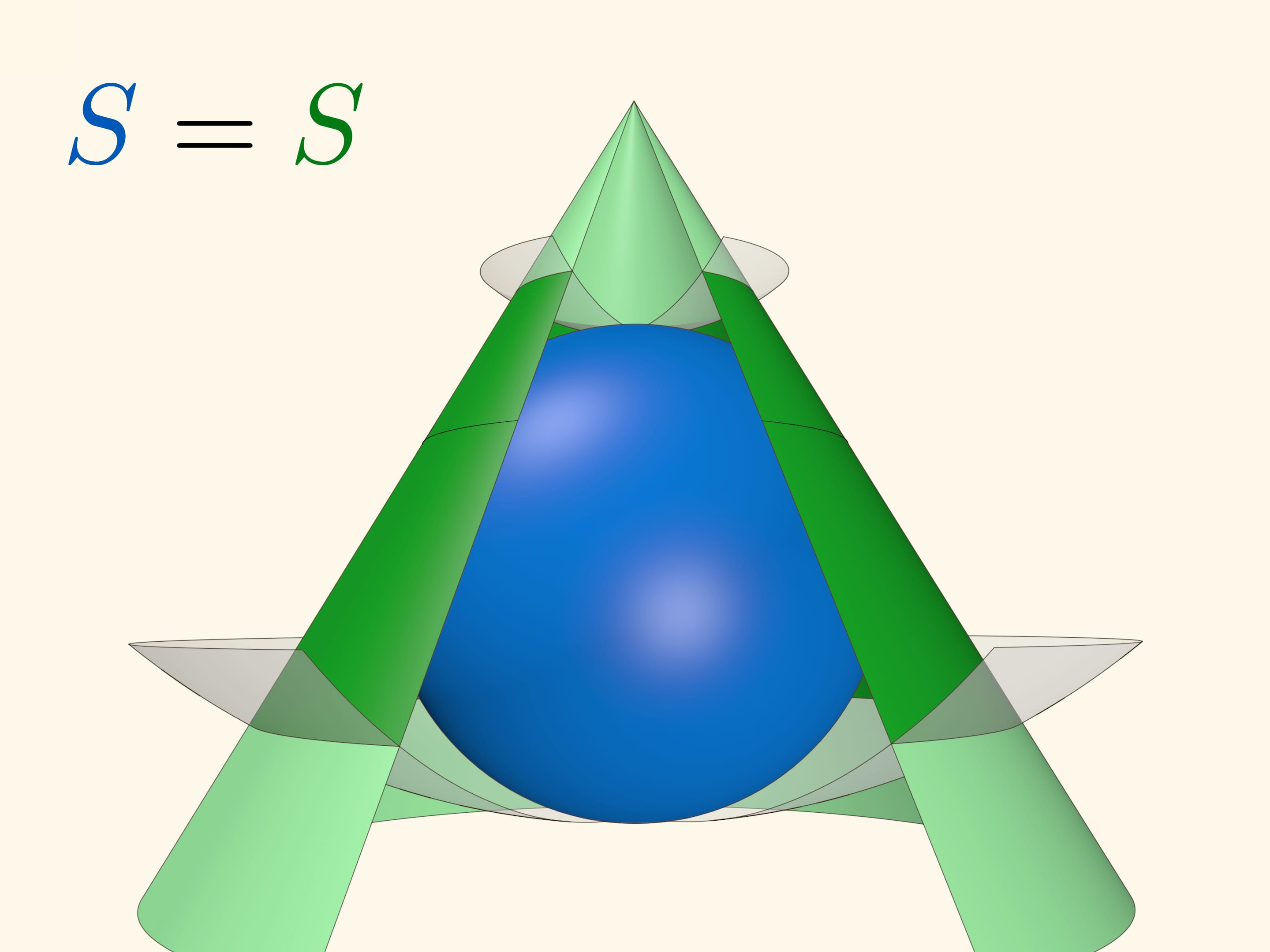
Круг, касающийся сферы в полюсе, можно считать предельным случаем конуса, касающегося сферы.
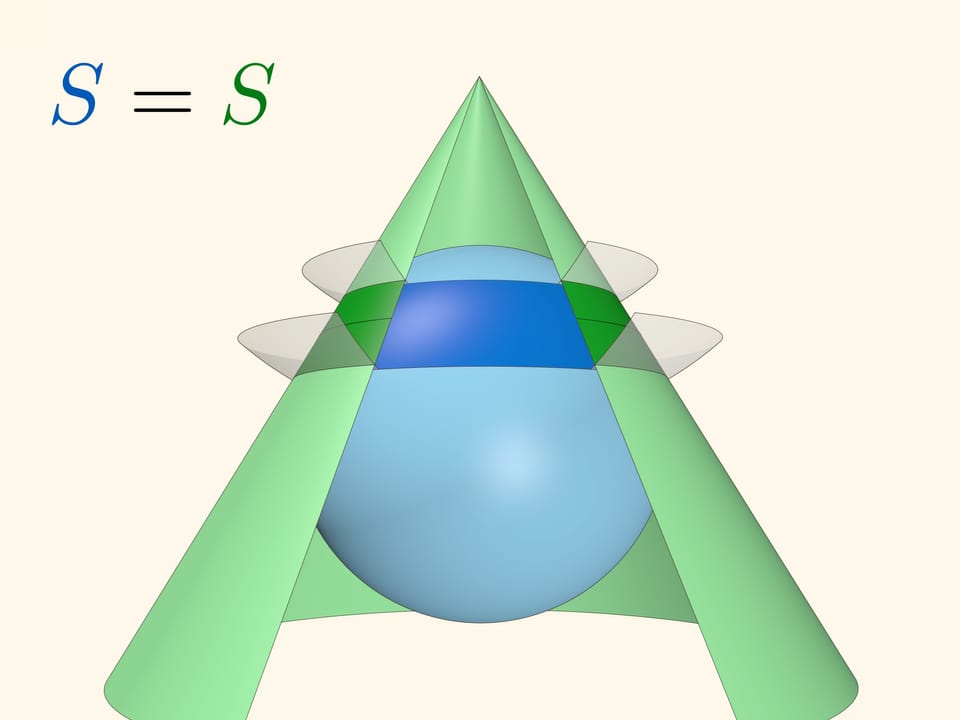
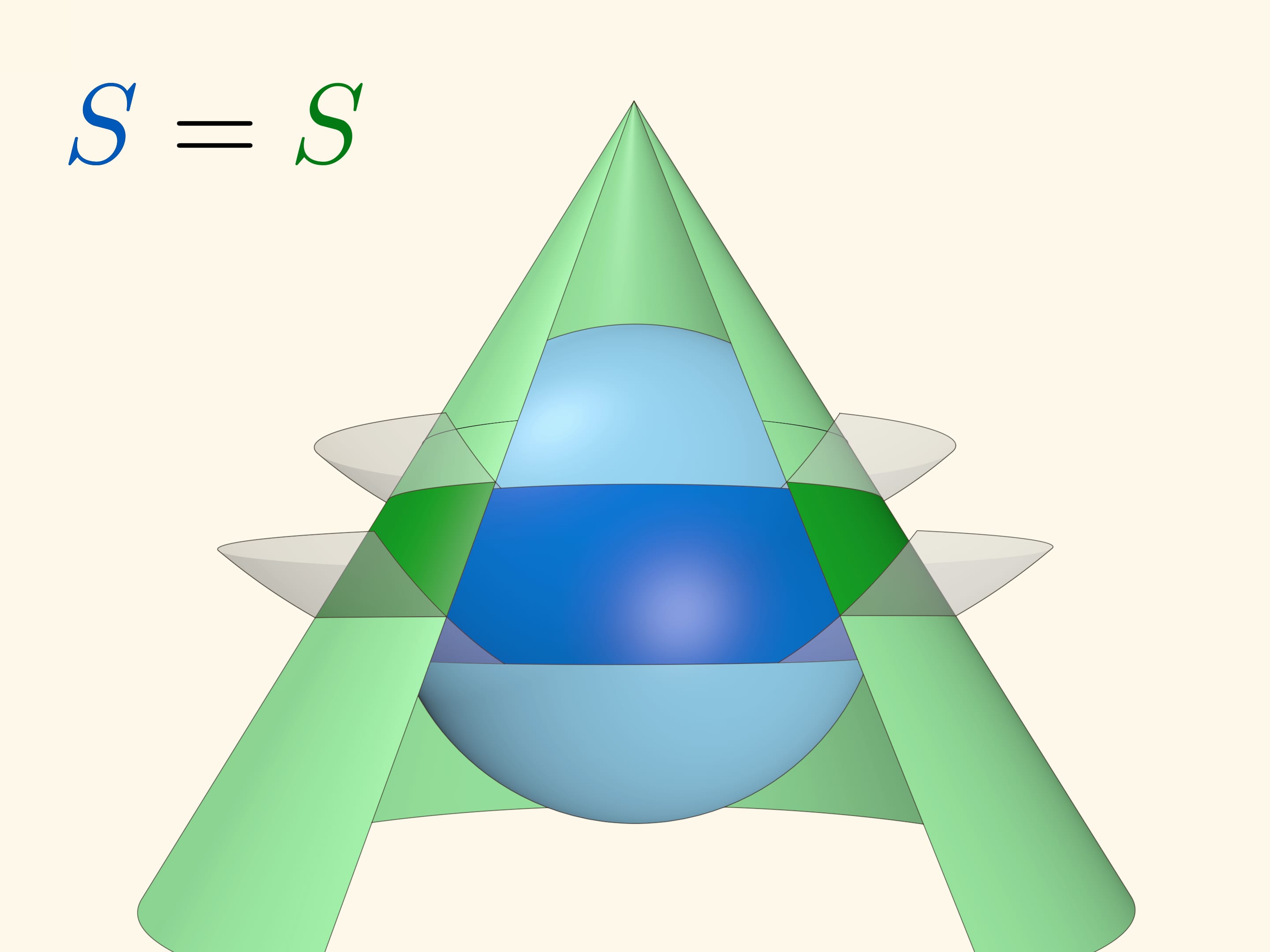
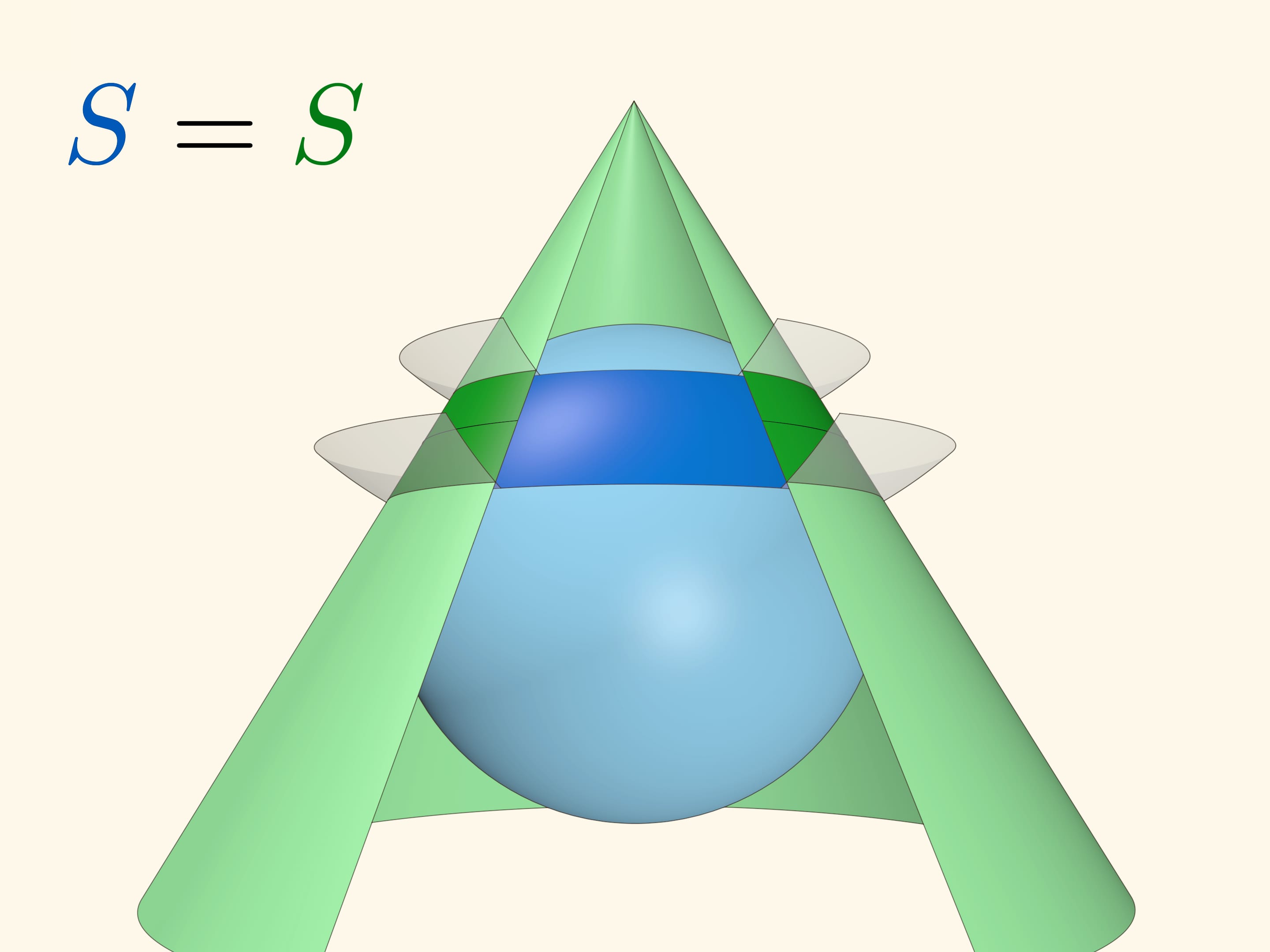
Рассмотрим две вспомогательные концентрические сферы с центром в вершине конуса. И на сфере, и на конусе эти сферы высекают кольца. Оказывается, что площади этих колец — на сфере и на конусе — равны.
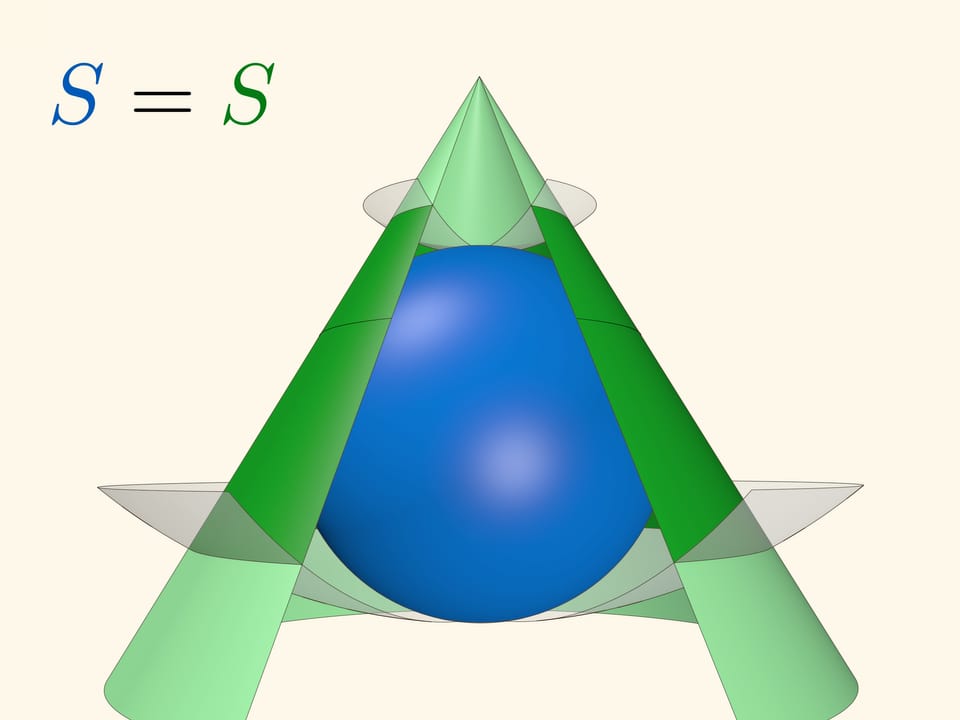
Равенство остаётся верным для любого положения концентрических сфер. Рассмотренный случай равенства площадей шапочки на сфере и соответствующего круга, касающегося сферы, получается из конического: радиус одной из концентрических сфер следует положить нулю, а вершину конуса поместить в полюс сферы.
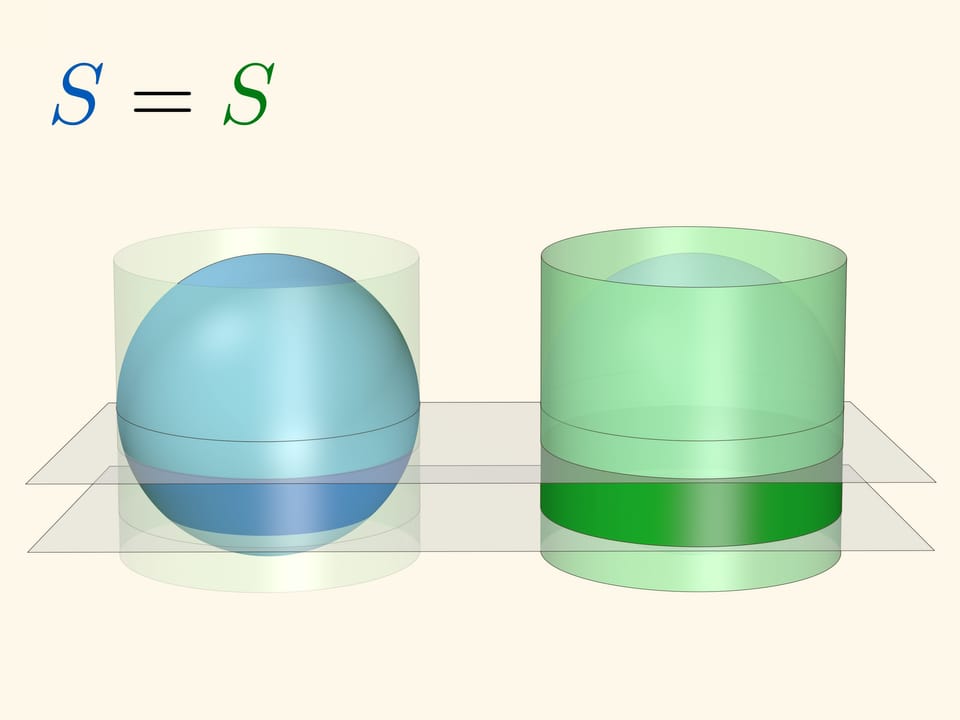
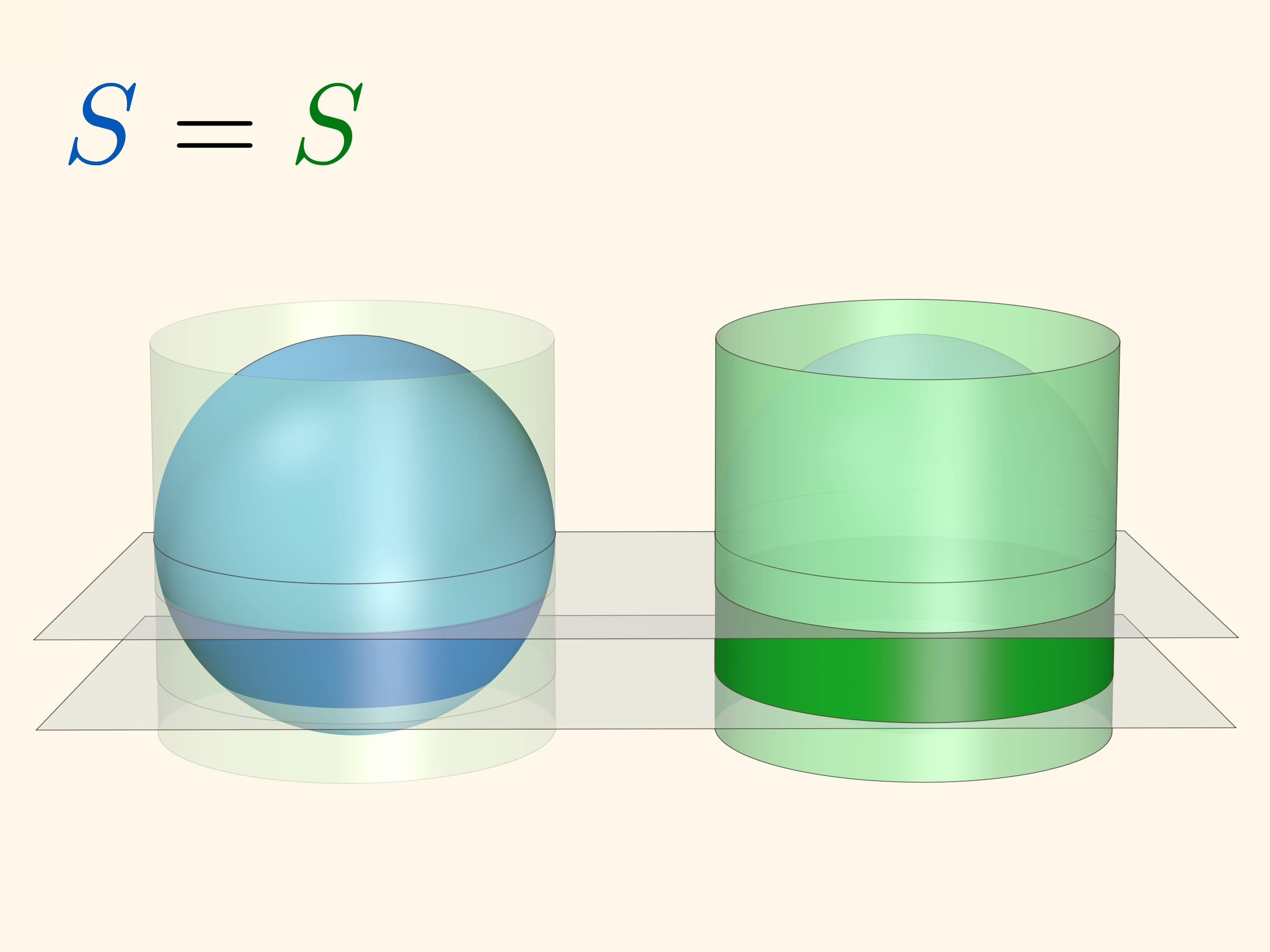
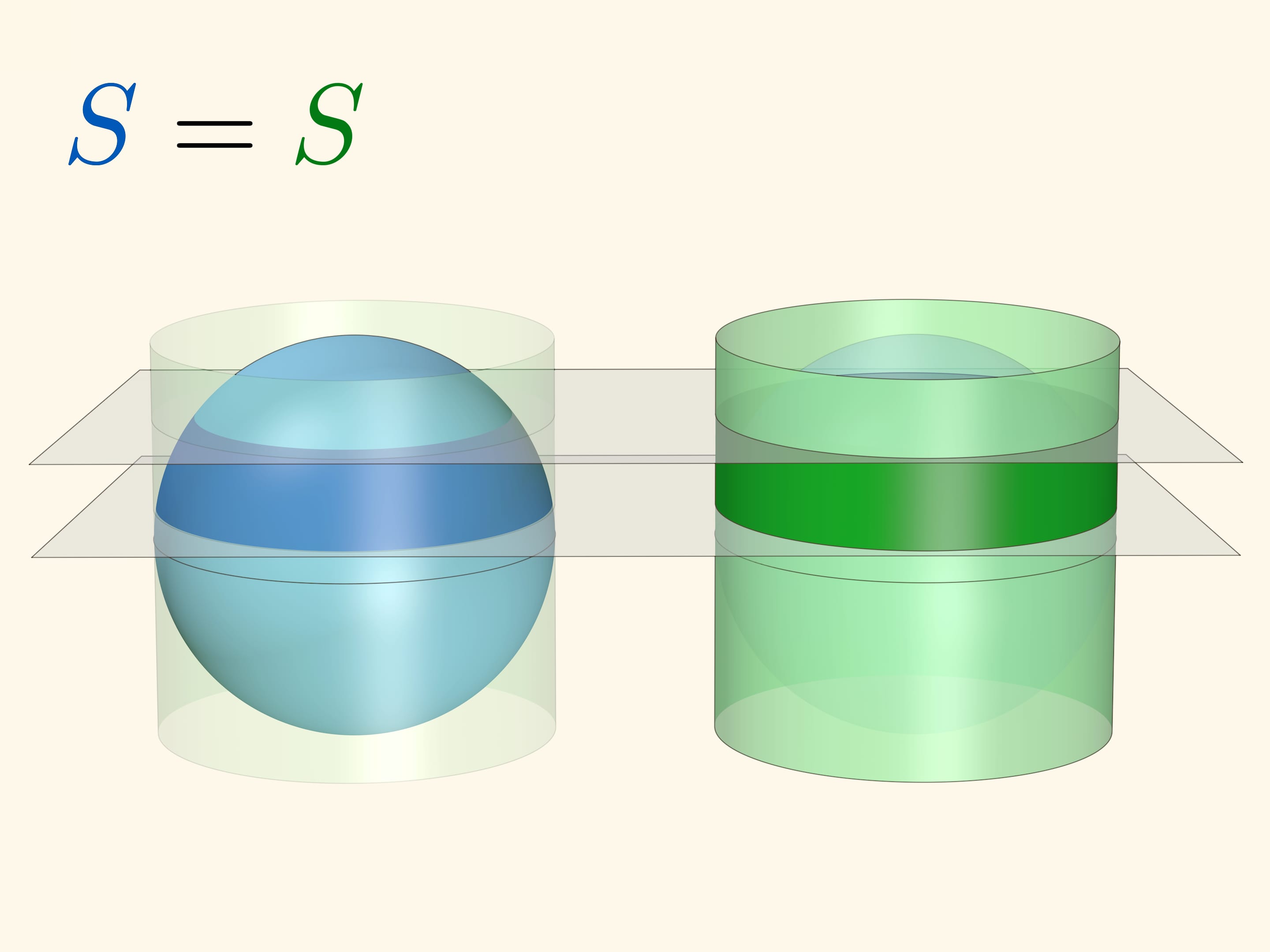
Если же вершину конуса «угнать» на бесконечность, то конус перейдёт в цилиндр, касающийся сферы по экватору. Концентрические вспомогательные сферы перейдут в плоскости.
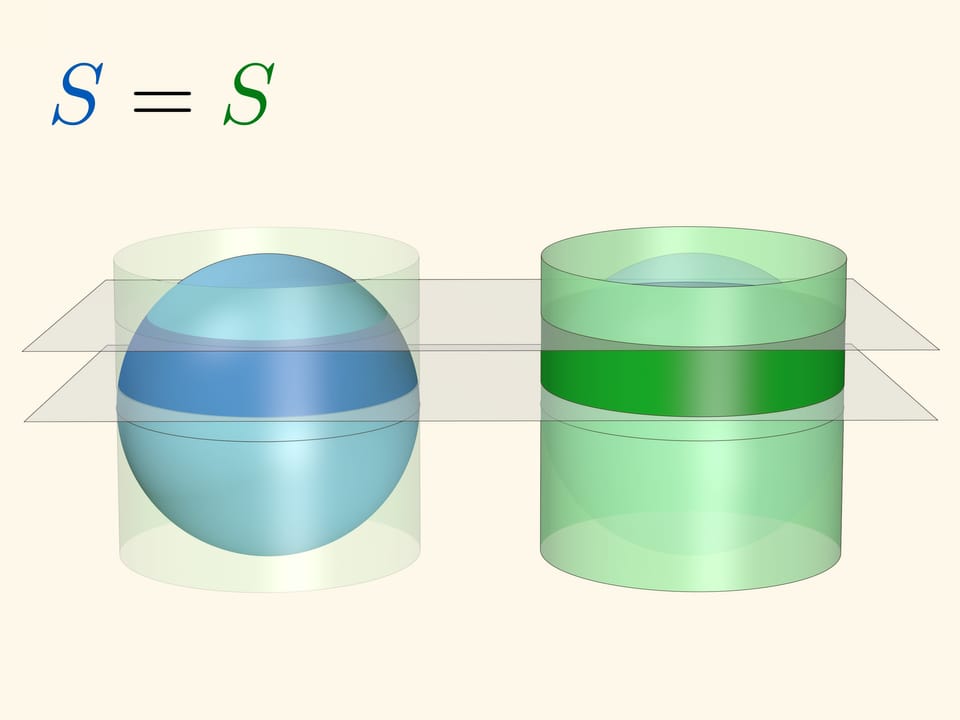
Площадь сферического кольца, вырезаемого двумя параллельными плоскостями, равна площади соответствующего цилиндрического кольца (плоскости перпендикулярны оси цилиндра). Это приводит к интересному наблюдению: площадь кольца на глобусе зависит только от расстояния между секущими плоскостями, но не зависит от близости кольца к экватору или полюсу. «Съедобное» толкование: если круглый неочищенный апельсин нарезать на ломтики одинаковой толщины, то и площадь шкурки у всех кусков будет одинакова.
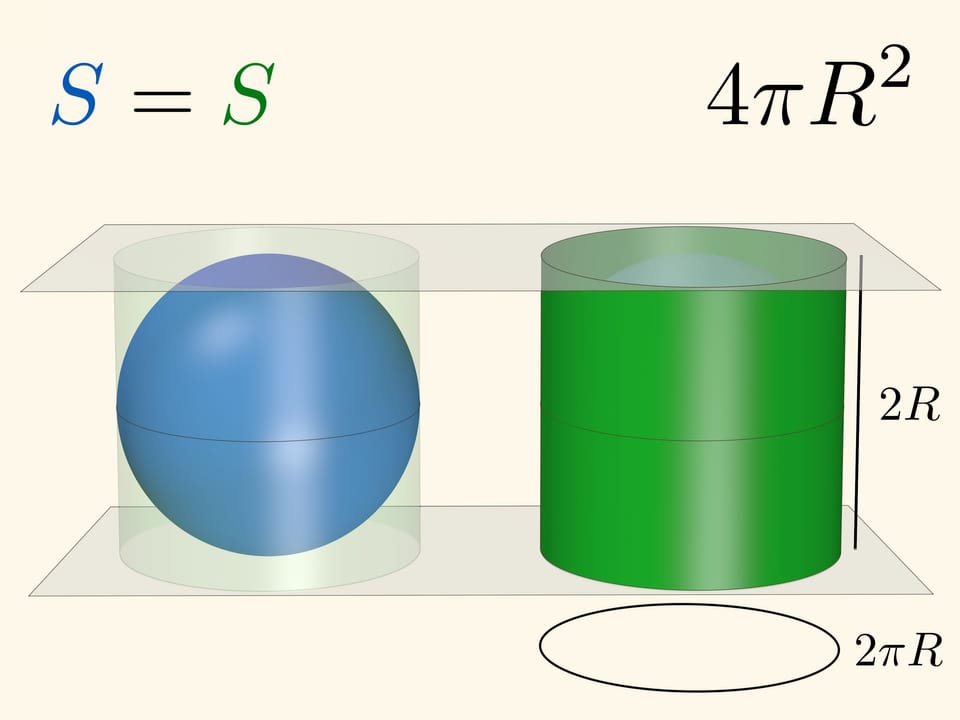
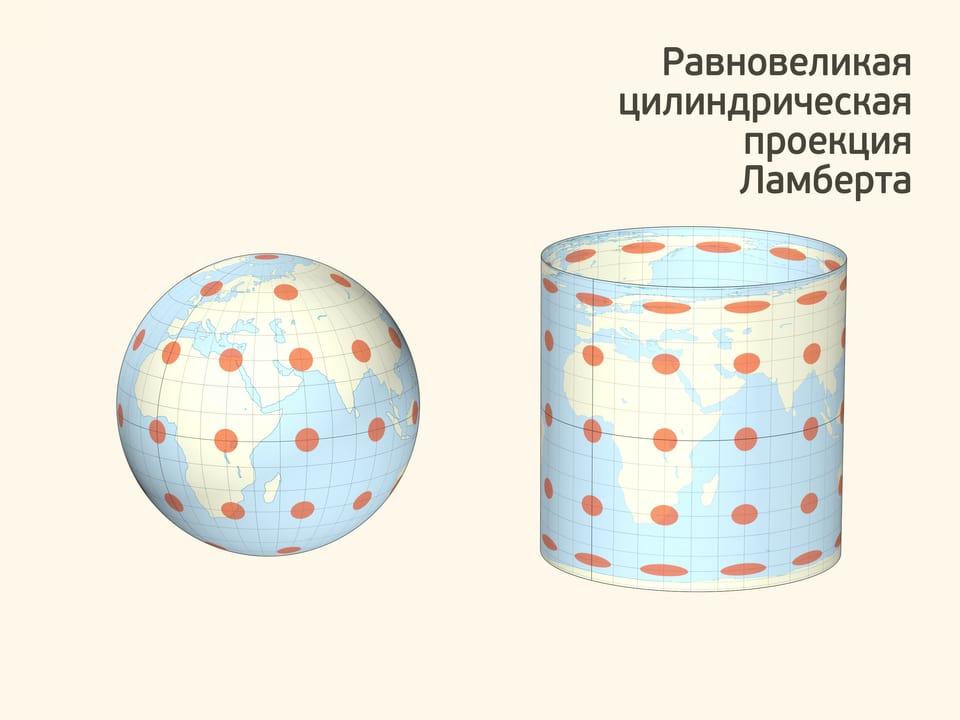
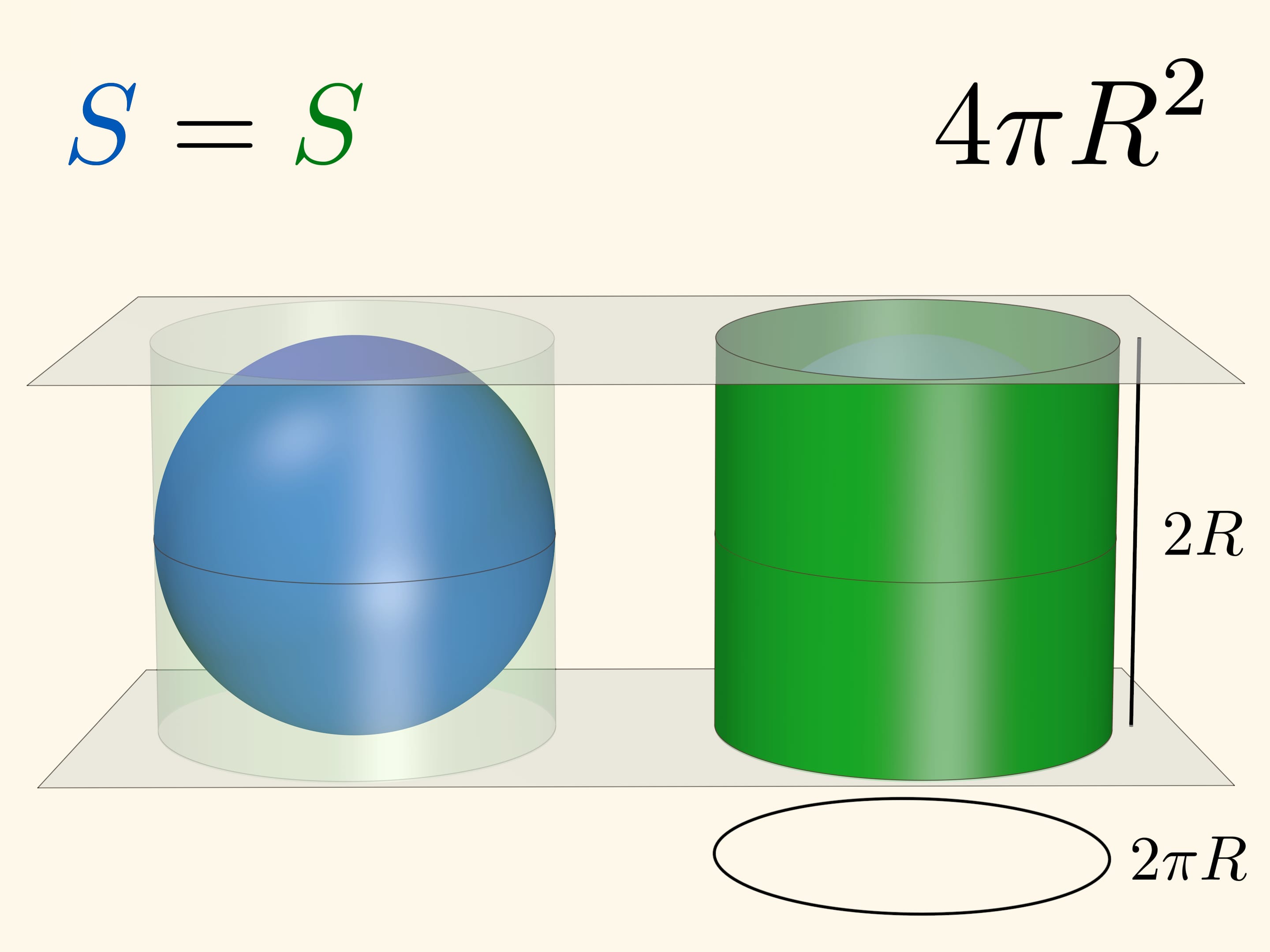
Сравнение площади кольца на сфере и кольца на цилиндре позволяет посчитать площадь всей сферы. Когда плоскости касаются полюсов сферы расстояние между ними равно $2R$. А длина окружности цилиндра, касающегося сферы равна $2\pi R$. Разворачивая цилиндр в прямоугольник получаем $4\pi R^2$.
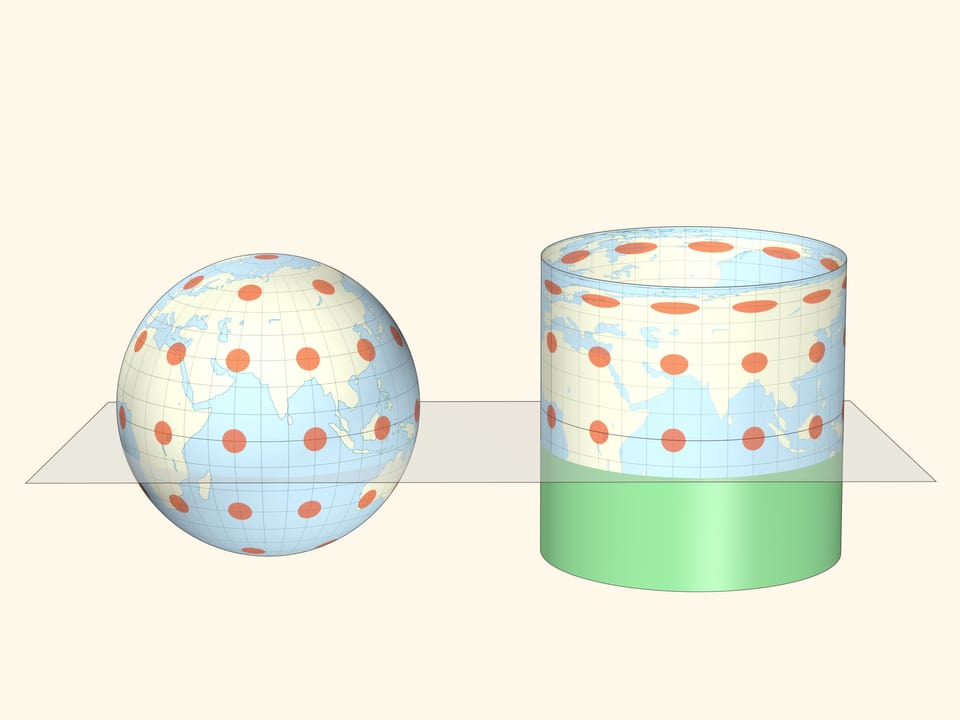
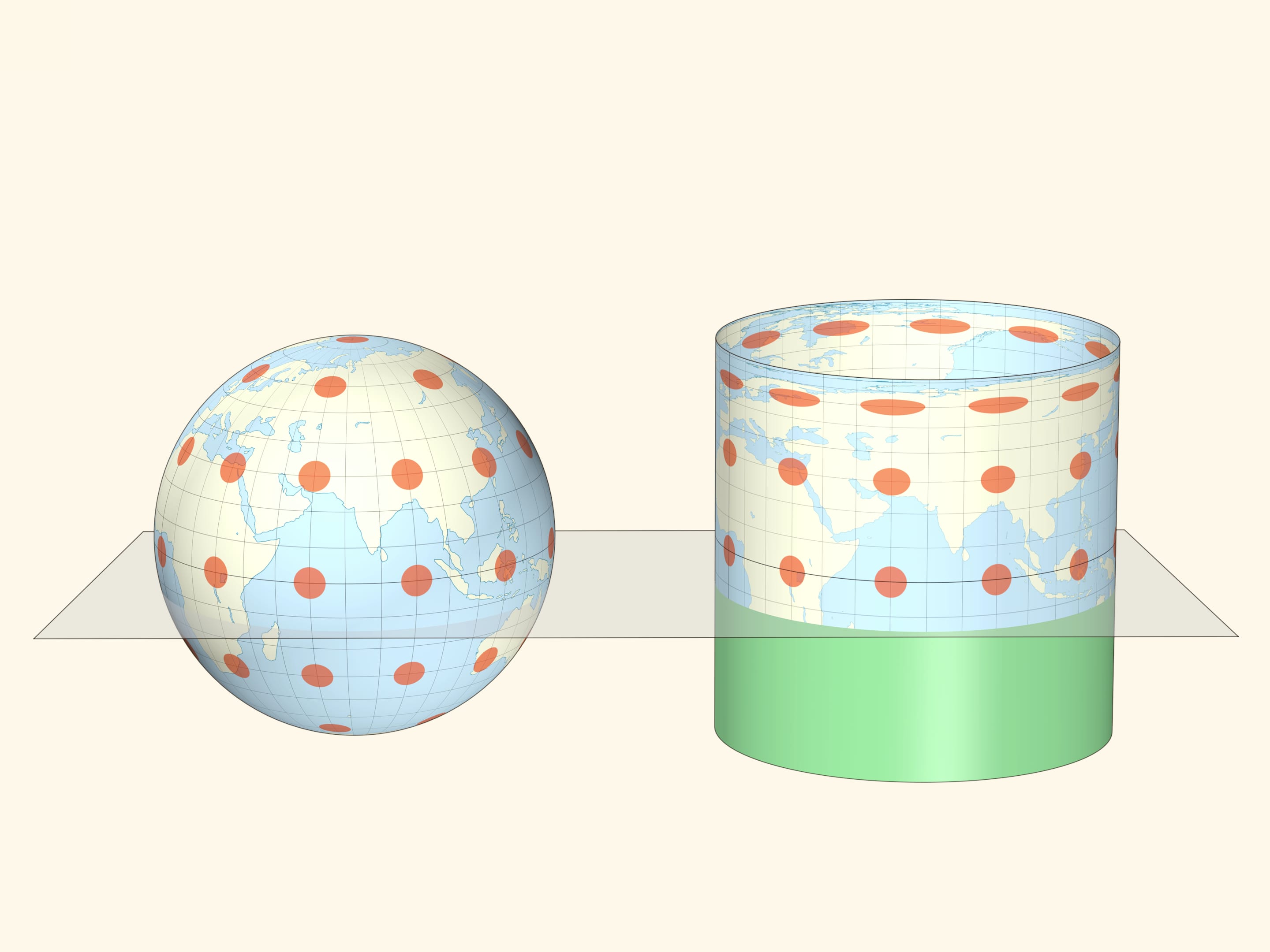
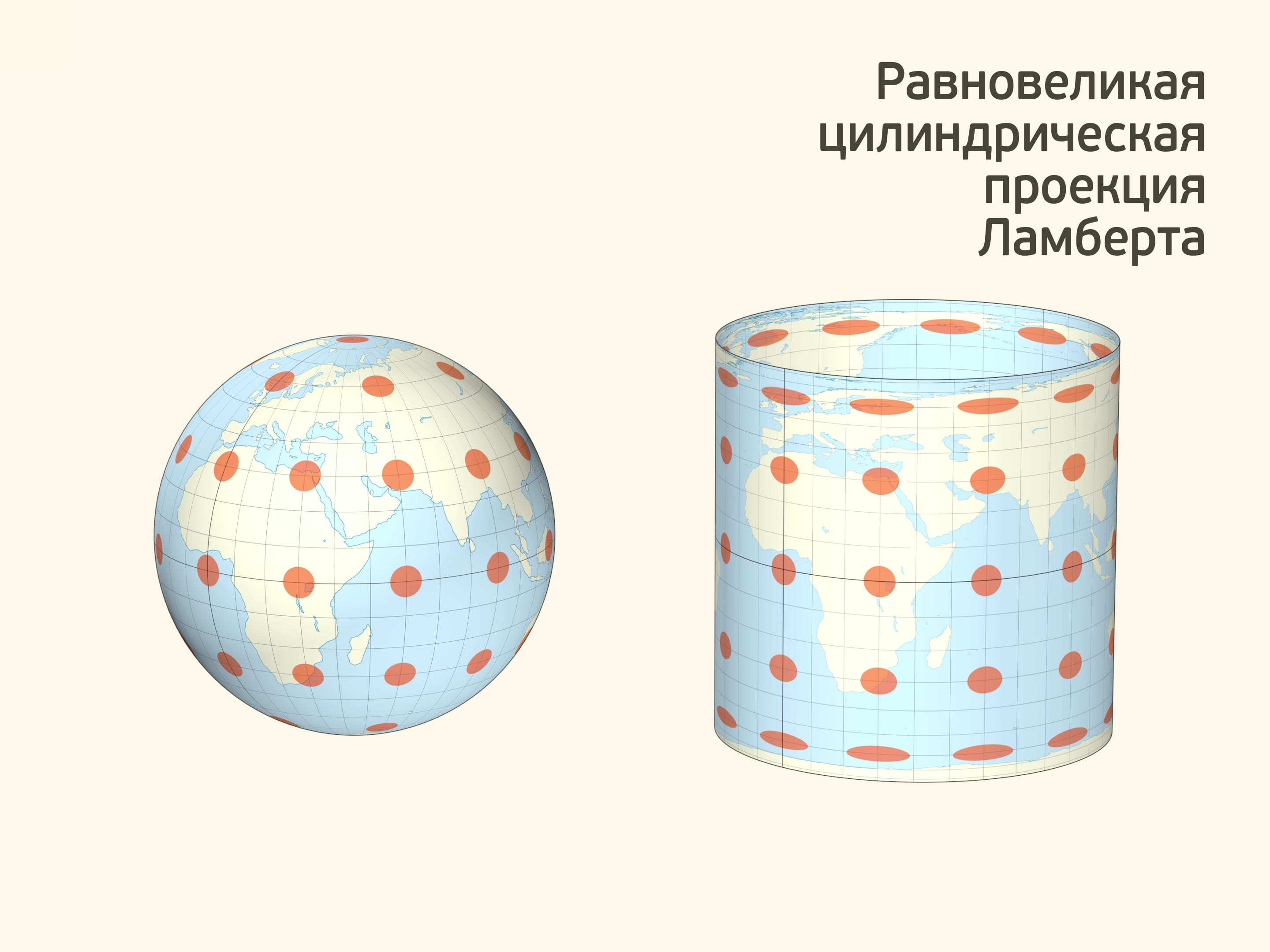
Перенося информацию с глобуса на сферу с сохранением высоты получаем равновеликую цилиндрическую картографическую проекцию Земли. Такая проекция, по рассмотренному выше свойству, сохраняет площади всех областей и тоже была разработана Ламбертом.
Утверждение про равенство площадей колец на сфере и на цилиндре называется леммой Архимеда и известно с давних времён. Утверждение про площадь сферической шапочки и площадь круга тоже довольно известно. Удивительно, что связывающая эти два случая конструкция — сравнение площадей колец на сфере и на конусе, заключённых между концентрическими сферами с центрами в вершине конуса — малоизвестна и, возможно, была открыта только в XXI веке.
Литература
Акопян А. В. Апельсины, канализационные люки и разрезание длинного прямоугольника // Журнал «Квант». — 2021. — № 9. — Стр. 40—43.
Vin De Silva. A Generalisation of Archimedes' Hatbox Theorem // The Mathematical Gazette. — 2006. — Vol. 90, № 517. — P. 132—134.
Картографические проекции // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 136—145, 342, 343.