Самым популярным «противопоставлением» евклидовой геометрии является геометрия Лобачевского. Но существует ещё одна геометрия, в которой не выполняется пятый постулат Евклида. В сферической геометрии через точку, не лежащую на прямой, нельзя провести ни одной прямой, параллельной данной. Но от евклидовой геометрии она отличается не только этим.
Сферическая геометрия — геометрия обычной сферы. Точки — точки сферы, прямые — большие круги (окружности): сечения сферы плоскостями, проходящими через её центр. В представляемой интерактивной модели точки можно двигать!
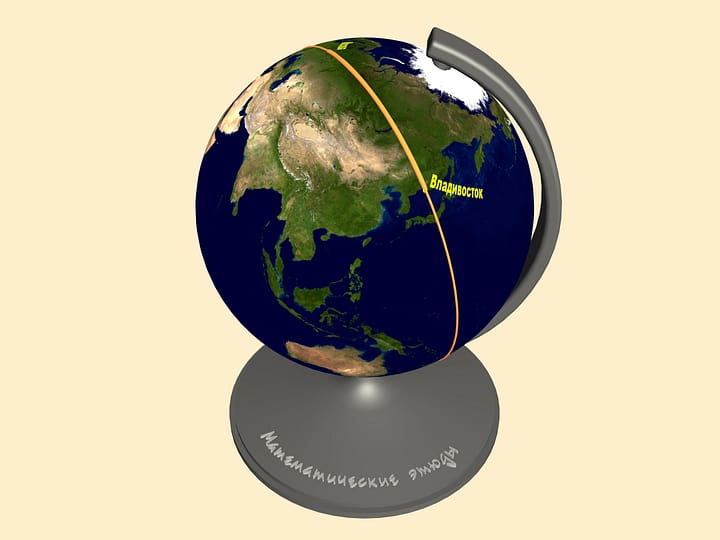
Через две близкие точки (не диаметрально противоположные) можно провести ровно одну прямую. Отрезок этой прямой — кратчайшее расстояние (по сфере) между этими точками. Если радиус сферы равен единице, то длина отрезка — это просто величина центрального угла в радианах.
Примерно по таким траекториям при учёте других ограничений и прокладываются маршруты самолётов.
В евклидовой геометрии через точку, не лежащую на прямой, можно провести ровно одну прямую, параллельную данной. В геометрии Лобачевского через точку, не лежащую на прямой, можно провести бесконечно много прямых, параллельных данной. (Параллельными называются прямые, не имеющие общих точек.)
В сферической геометрии через точку, не лежащей на прямой, нельзя провести ни одной прямой, параллельной данной: две различные прямые всегда имеют ровно две общие точки.
В евклидовой геометрии и в геометрии Лобачевского через две различные точки можно провести ровно одну прямую. В сферической геометрии через две близкие точки можно провести ровно одну прямую, а через диаметрально противоположные точки можно провести бесконечно много прямых.
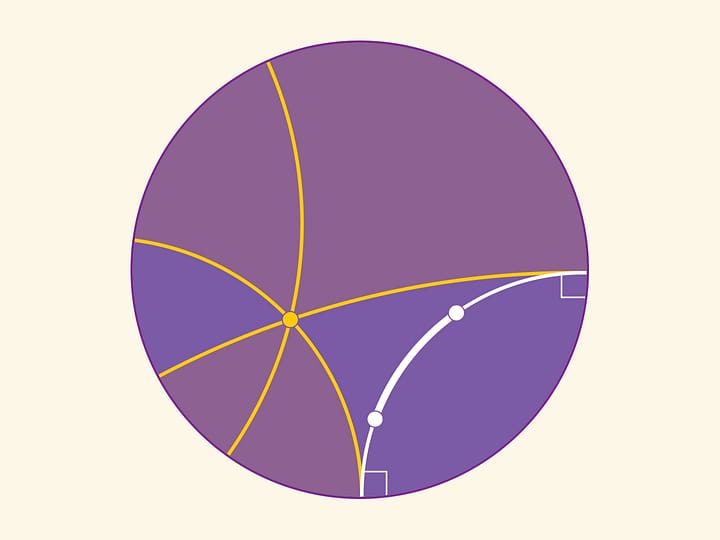
Окружность — геометрическое место точек, удалённых от данной точки на данное расстояние (в смысле рассматриваемой геометрии, в нашем случае — измеряемое по сфере). Окружности на сфере являются и окружностями в евклидовом смысле.
На сфере и радиус окружности, и длина окружности ограничены. Радиус не больше длины меридиана, а длина окружности не больше длины прямой — большого круга. (И это ещё одно принципиальное отличие сферической геометрии от евклидовой: третий постулат Евклида гласит, что из всякого центра всяким радиусом может быть описан круг.)
Длина окружности радиуса $r$ равна $2\pi\sin r$. (Отметим, что постоянство отношения длины окружности к её диаметру для любой окружности является эквивалентом пятого постулата Евклида.)
Формула для длины окружности говорит, что даже маленькая сферическая окрестность точки не является плоской: даже при маленьких радиусах длина окружности на сфере не равна длине окружности на плоскости. Более подробно аргумент Эйлера и разбор формул для длины окружности и площади круга можно посмотреть в статье Искривлённые миры и фильме Картографические проекции: все карты врут.
Треугольник — три точки, не лежащие на одной прямой и соединённые геодезическими линиями, кратчайшими: отрезками прямых, проходящих через эти точки.
Кратчайшая на сфере — меньшая дуга большой окружности, проходящей через точки. Угол сферического треугольника — это угол между дугами окружностей, и он равен величине двугранного угла, образованного плоскостями, которые содержат соответствующие отрезки (прямые).
На плоскости доказательство того, что сумма (внутренних) углов треугольника равна двум прямым, т.е. $\pi$, явно использует параллельные прямые. На сфере параллельных прямых нет. Сумма углов треугольника в сферической геометрии бывает разной, но всегда больше $\pi$.
Например, можно построить треугольник с тремя прямыми углами: одной вершиной в «полюсе» и двумя на «экваторе».
На плоскости треугольники могут быть подобными: с одинаковыми углами, но разными длинами сторон. В сферической геометрии так не бывает: сферический треугольник полностью определяется своими углами. Действительно, треугольник высекается на сфере центральным трёхгранным углом, а трёхгранный угол задаётся тремя углами (либо тремя плоскими, либо тремя двугранными).
Площадь сферического треугольника с углами $\alpha$, $\beta$, $\gamma$ равна $$(\alpha+\beta+\gamma-\pi)\cdot R^2.$$ В сферической геометрии площади всех треугольников ограничены. (А существование треугольника сколь угодно большой площади равносильно пятому постулату Евклида.)
Для доказательства формулы площади треугольника используется фигура, определённая только в сферической геометрии, — двуугольник: область, ограниченных двумя прямыми, проходящими через две диаметрально противоположные точки.
Площадь двуугольника пропорциональна углу между прямыми и составляет от площади сферы такую же часть, как угол $2\alpha$ от угла $2\pi$. Поэтому его площадь на сфере радиуса $R$ равна $\frac{2\alpha}{2\pi}\cdot 4\pi R^2=4\alpha R^2$.
Для каждого из углов треугольника рассмотрим соответствующий ему двуугольник.
Эти три двуугольника покрывают треугольник и симметричный ему треугольник в три слоя, а остальную часть сферы — в один слой. Площадь всей сферы равна $4\pi R^2$, и указанная площадь треугольника $S$ находится из уравнения $$4\alpha R^2+4\beta R^2+4\gamma R^2-2S-2S=4\pi R^2.$$
Движение — отображение рассматриваемого пространства в себя, сохраняющее попарные расстояния между точками. И в евклидовой геометрии, и в геометрии Лобачевского, и в сферической геометрии любое движение может быть представлено как композиция отражений.
Движения евклидовой плоскости описывает теорема Шаля. В частности, любое собственное движение есть композиция двух симметрий: относительно параллельных прямых — параллельный перенос, относительно пересекающихся прямых — поворот.
На сфере параллельных прямых не бывает и собственные движения в сферической геометрии описываются проще, чем в евклидовой: это всегда поворот.
Евклидову плоскость можно замостить одинаковыми правильными треугольниками, квадратами, шестиугольниками. В сферической геометрии возможны замощения одинаковыми правильными треугольниками, четырёхугольниками, пятиугольниками. Эти замощения отвечают пяти правильным многогранникам евклидова трёхмерного пространства: они являются проекциями многогранников из центра на описанную сферу.
- Тетраэдр
- Куб
- Октаэдр
- Додекаэдр
- Икосаэдр
Возможность замощения одинаковыми правильными $n$-угольниками, встречающимися по $k$ в каждой вершине, определяется величиной $\frac1n+\frac1k$. В евклидовой геометрии замощения возможны при $\frac1n+\frac1k=\frac12$; в сферической геометрии — при $\frac1n+\frac1k\gt\frac12$; а в геометрии Лобачевского — при $\frac1n+\frac1k\lt\frac12$.
Неравенству для сферической геометрии удовлетворяют и две серии, «двойственные» друг другу. Произвольное число двуугольников, сходящихся в полюсах: $n=2$, $k\gt 3$. Двойственная серия: экватор равномерно разделён $n$ точками, которые являются вершинами многоугольника в виде полусферы, два таких многоугольника встречаются по вершинам на экваторе — $n\gt 3$, $k=2$.
Сферическая геометрия изучалась математиками-астрономами ещё в античные времена. Например, главным трудом Менелая Александрийского (Μενέλαος ὁ Αλεξανδρεύς), жившего около 100 года нашей эры, была книга «Сферика». Но, как уже было сказано, сферическая геометрия отличается от евклидовой даже на уровне постулатов из «Начал» не только пятым постулатом. Поэтому именно геометрия Лобачевского стала первым примером, где первые четыре постулата Евклида выполняются, а пятый — нет.
Литература
Менелай Александрийский. Сферика.
Тайманов И. А. Искривлённые миры // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 222—227.