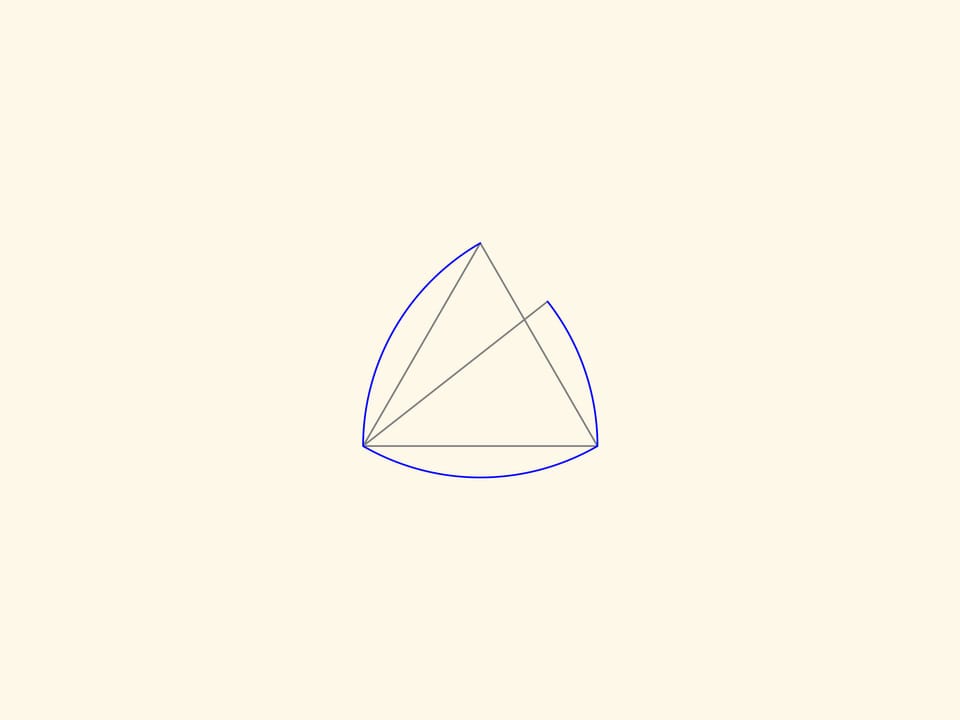
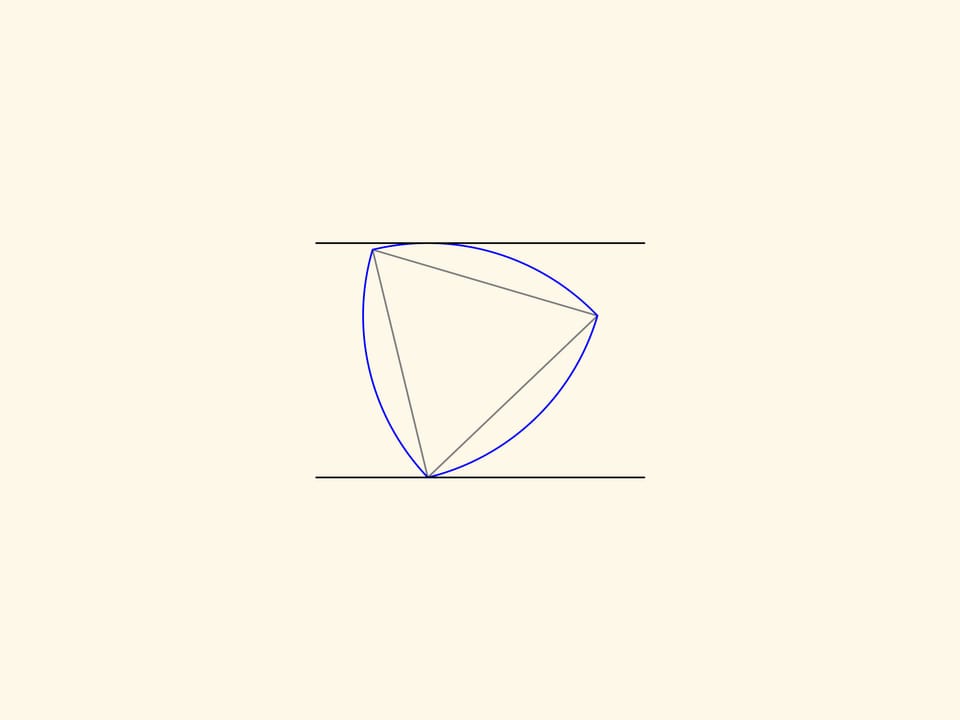
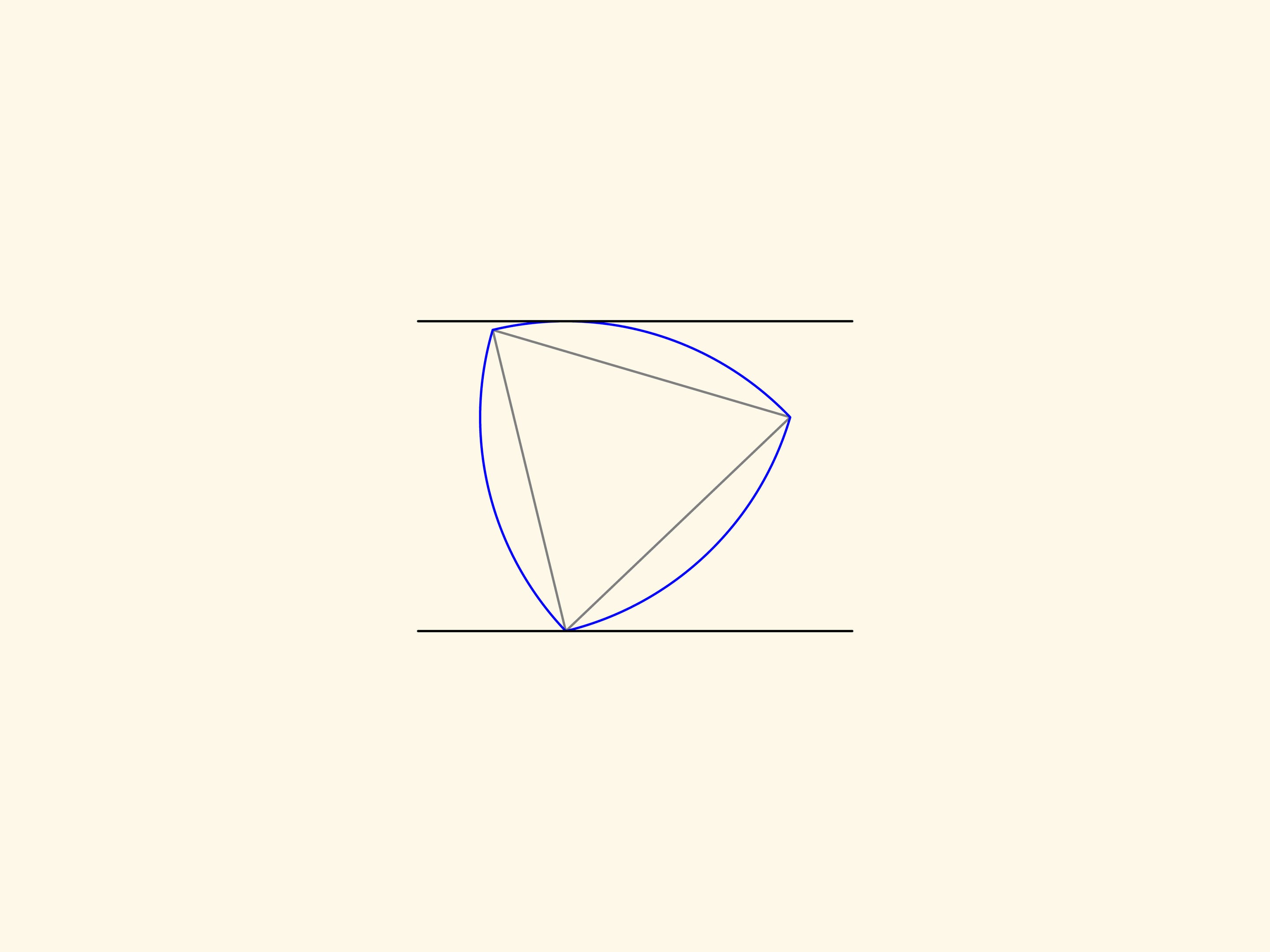
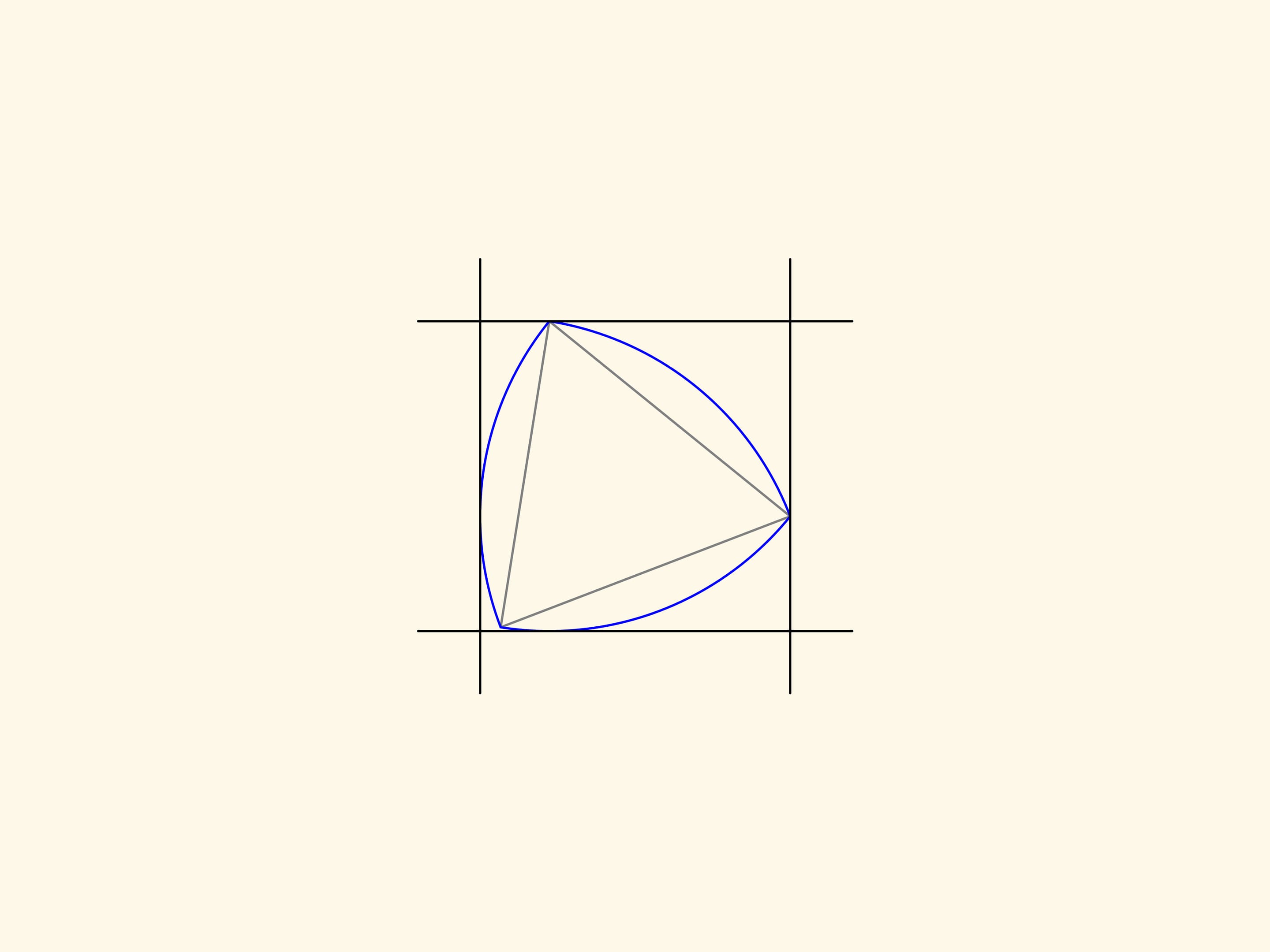
Треугольник Рело — плоская фигура постоянной ширины — его можно вращать между двух параллельных прямых, расположенных на фиксированном расстоянии друг от друга, и он будет постоянно касаться их обеих.
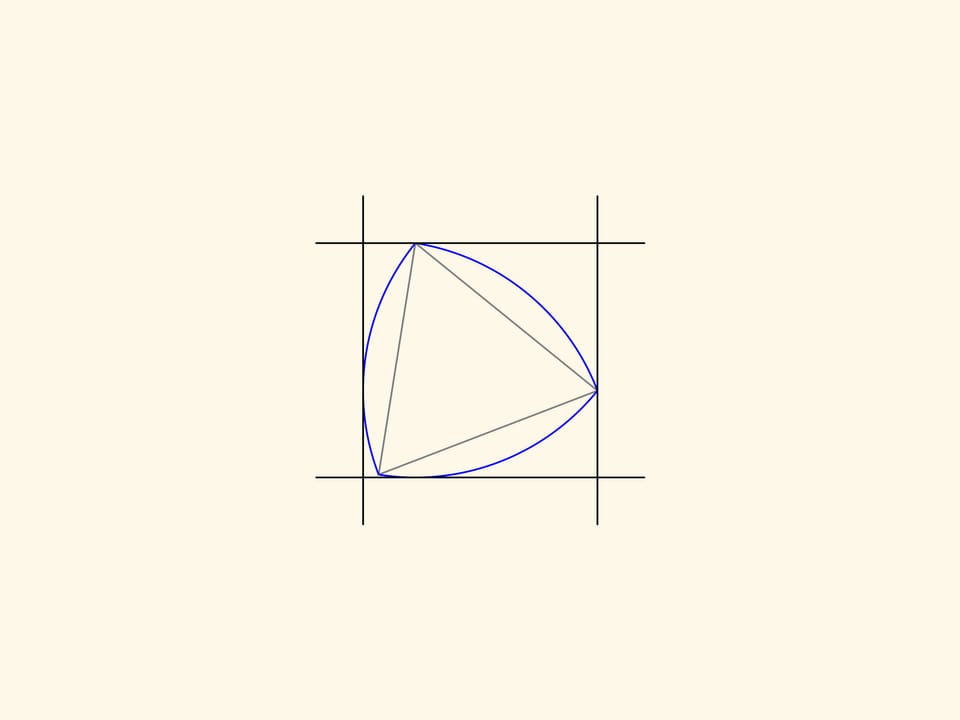
Добавим еще пару параллельных прямых, касающихся треугольника Рело и образующих с уже имеющимися прямой угол. Тем самым получим квадрат. Если вращать треугольник Рело специальным образом, то он будет постоянно находиться внутри квадрата и в любой момент касаться всех его сторон.
Если быть более точным, то надо рассматривать квадрат с немного скругленными углами. При этом треугольник Рело является в этом «квадрате» ротором минимальной площади — той фигурой, которая при любом повороте будет касаться всех сторон, и при этом более маленькой по площади фигуры с таким условием не существует.
Кроме окружности и треугольника Рело бывают и другие фигуры постоянной ширины. На любом правильном нечетном $n$–угольнике, так же как и на треугольнике, можно построить кривую постоянной ширины. Бывают несимметричные кривые постоянной ширины.
Но бывает и бесконечно много фигур постоянной ширины, построенных именно на правильном треугольнике, и не подобных ни друг другу, ни треугольнику Рело.
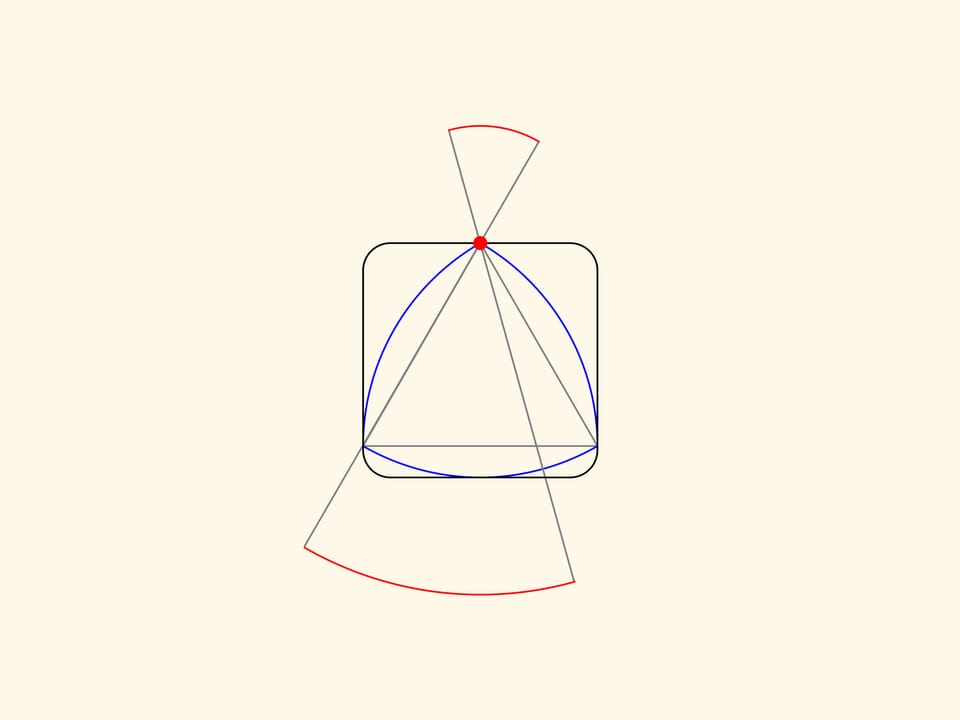
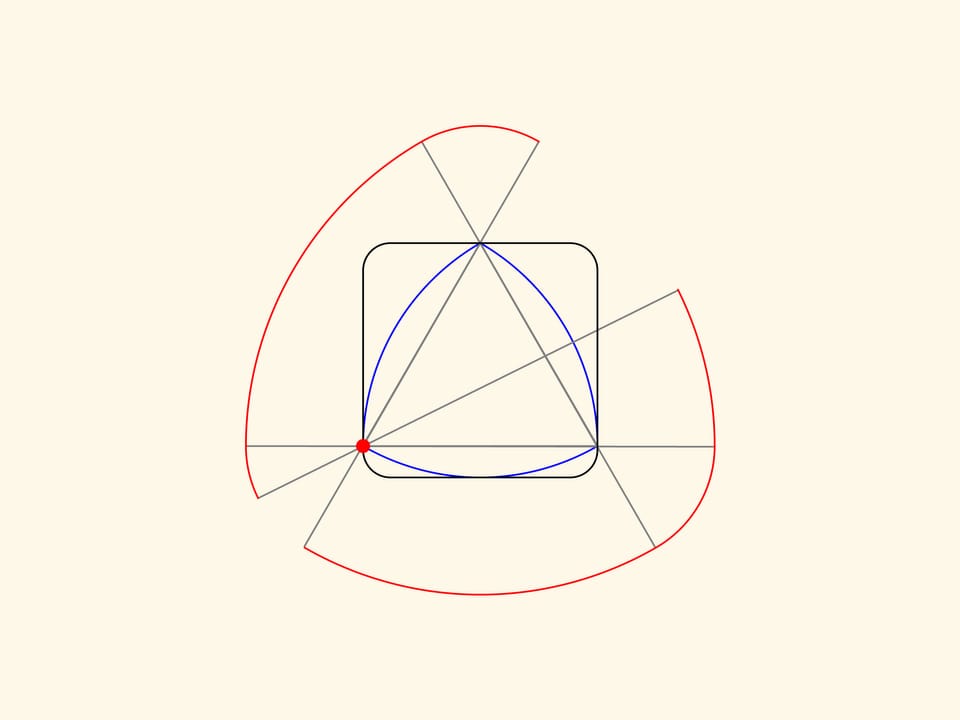
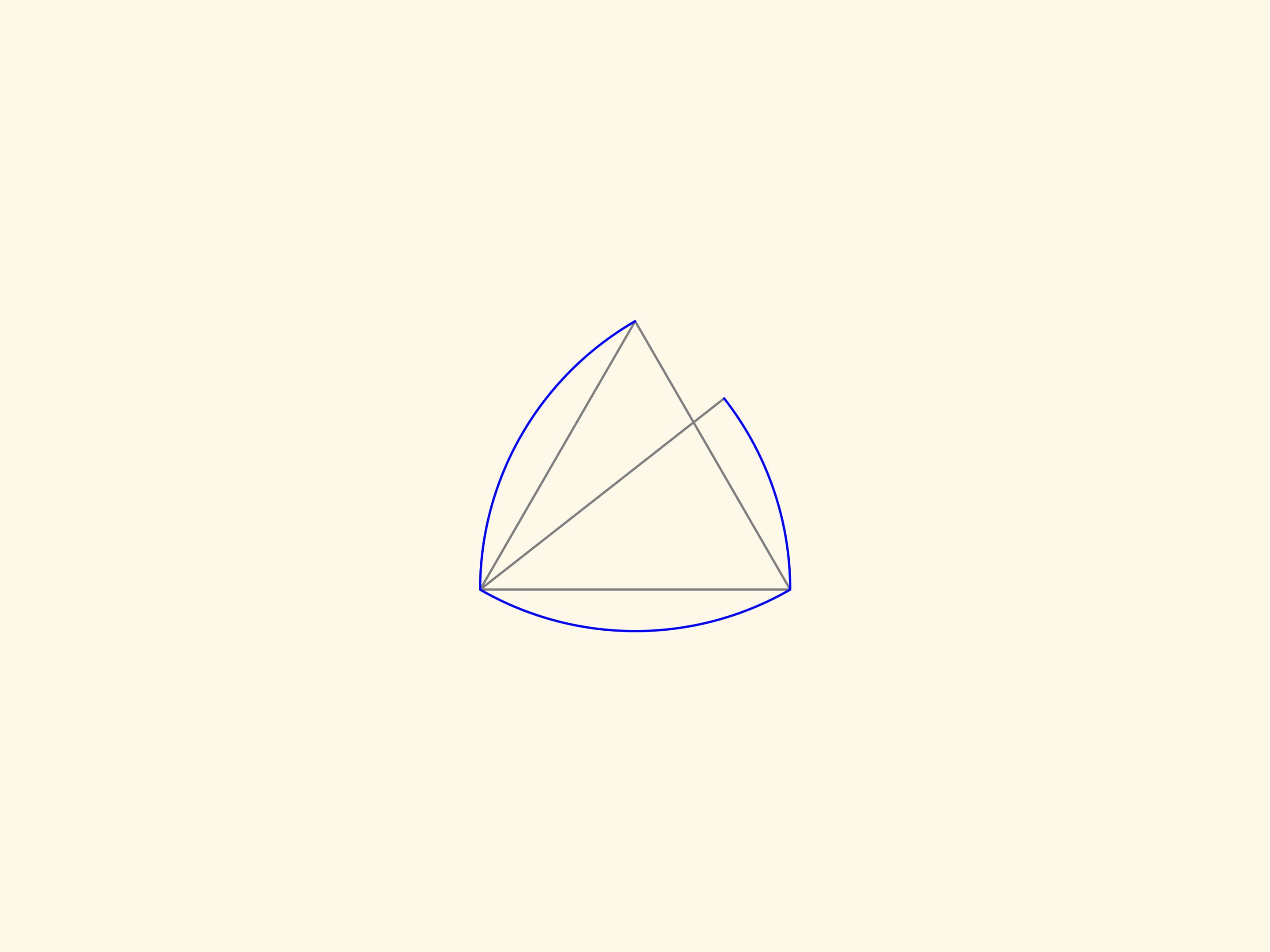
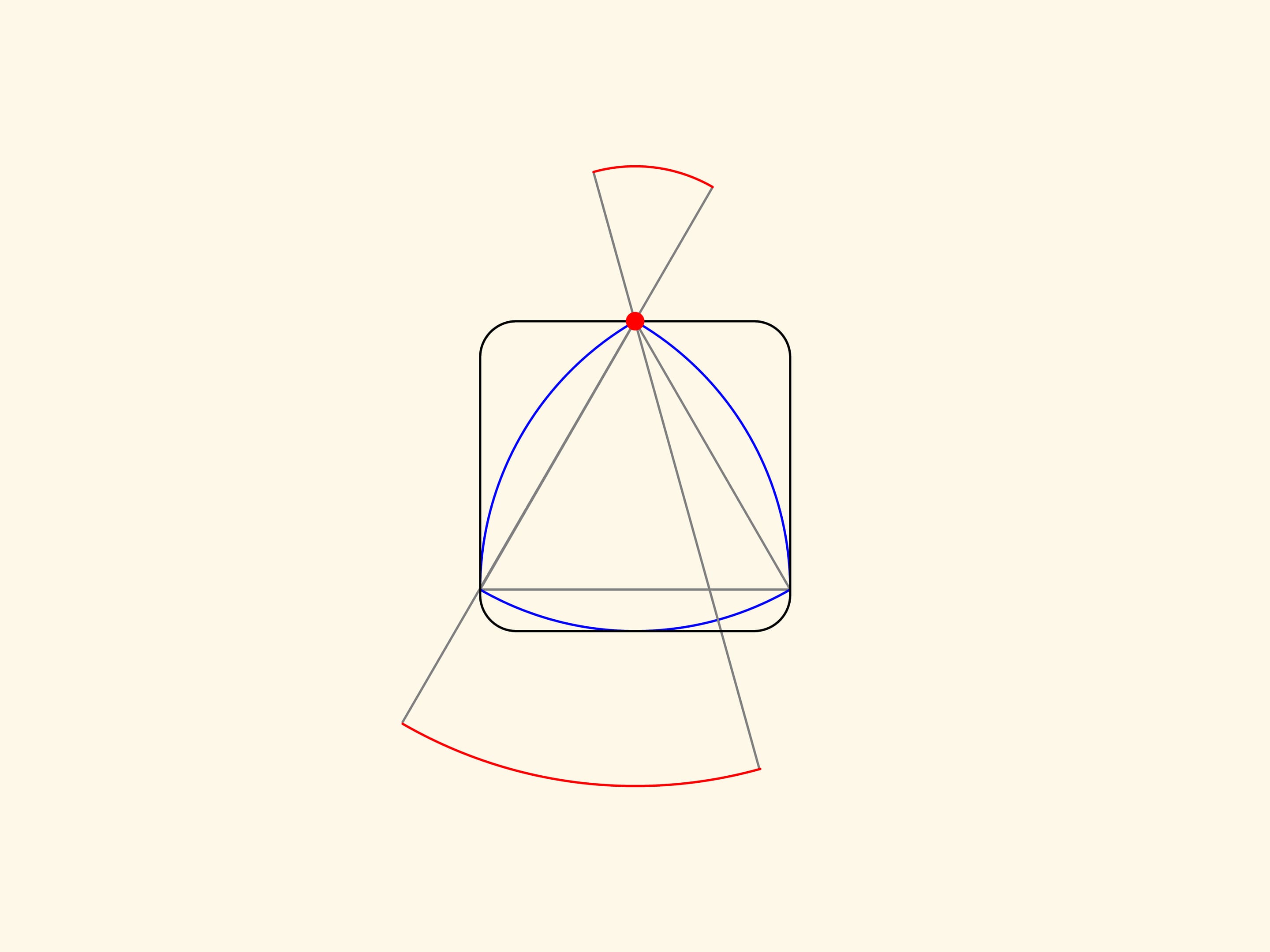
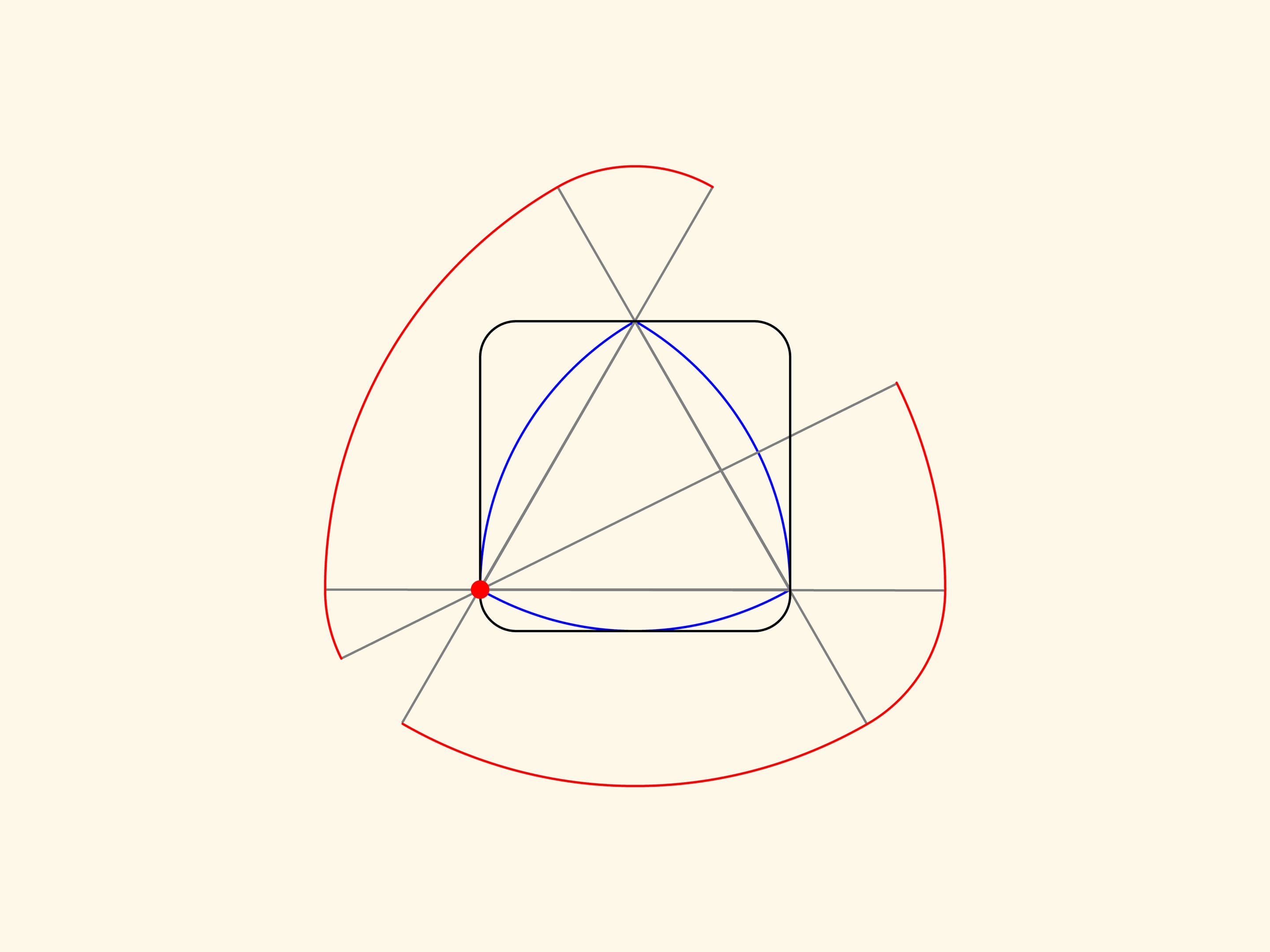
Продолжим какую–нибудь сторону правильного треугольника за обе вершины на одинаковое расстояние. Провращаем получившийся отрезок вокруг одной из вершин и проследим за траекториями его концов. Полученные большая и малая дуги будут частью кривой, ограничивающей фигуру постоянной ширины, которая строится. Провращаем этот же отрезок вокруг другой вершины, а затем вокруг оставшейся третьей вершины.
Получившаяся красная кривая будет состоять из трех дуг большого радиуса и трех — малого. Можно доказать, что она является границей фигуры постоянной ширины. При этом неважно, насколько продолжать сторону за вершины, главное, чтобы за обе вершины сторона продолжалась на одинаковое расстояние.
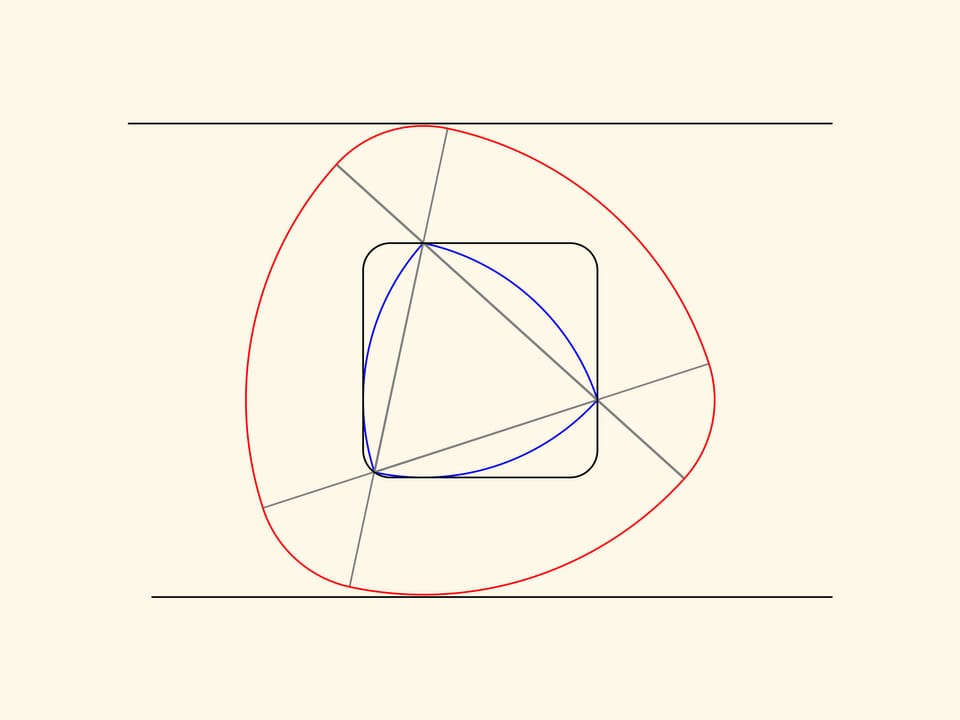
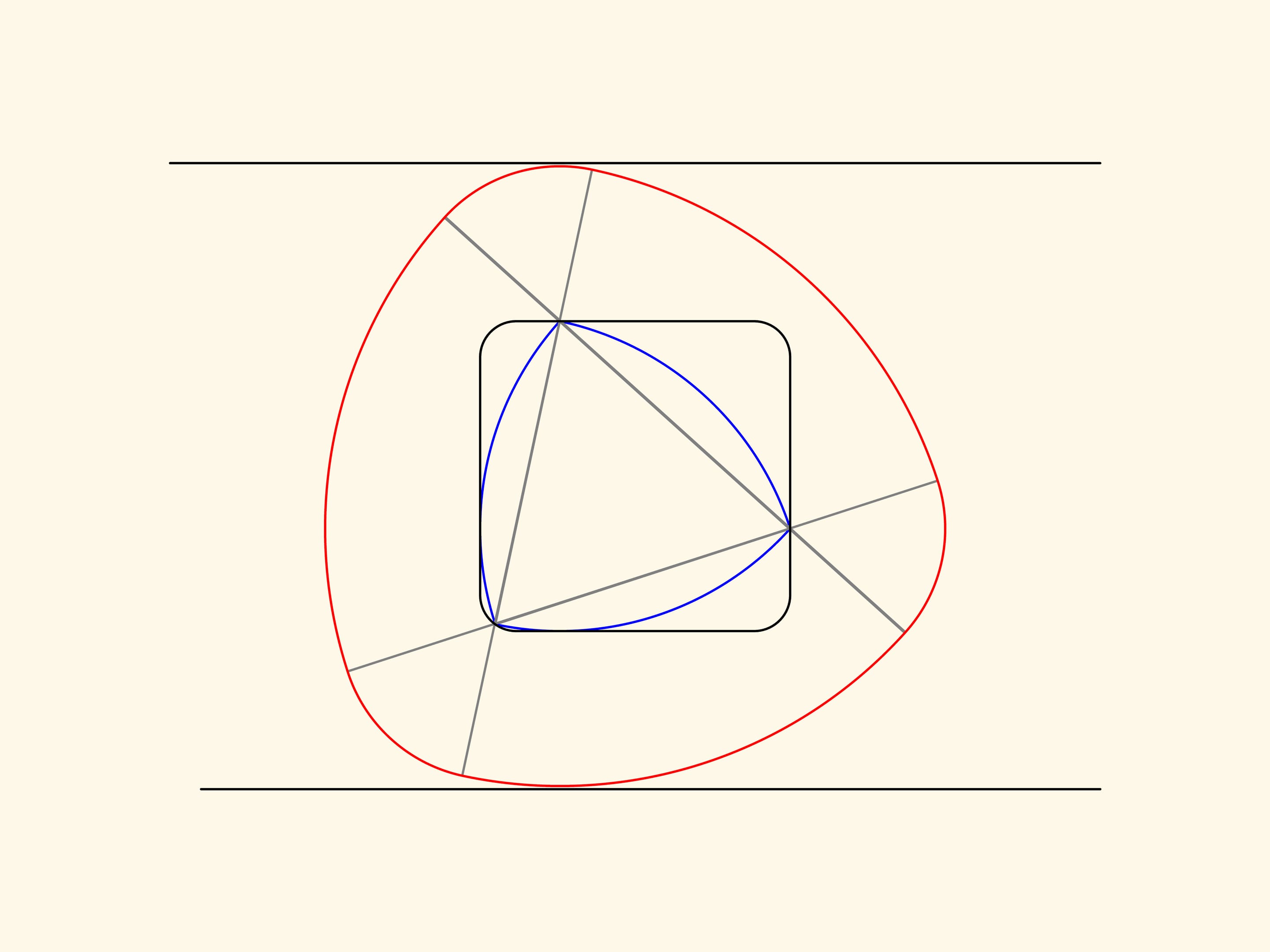
Если начать вращать треугольник Рело в квадрате, то связанная с ним красная кривая будет вращаться между двух параллельных прямых, неподвижных относительно квадрата.
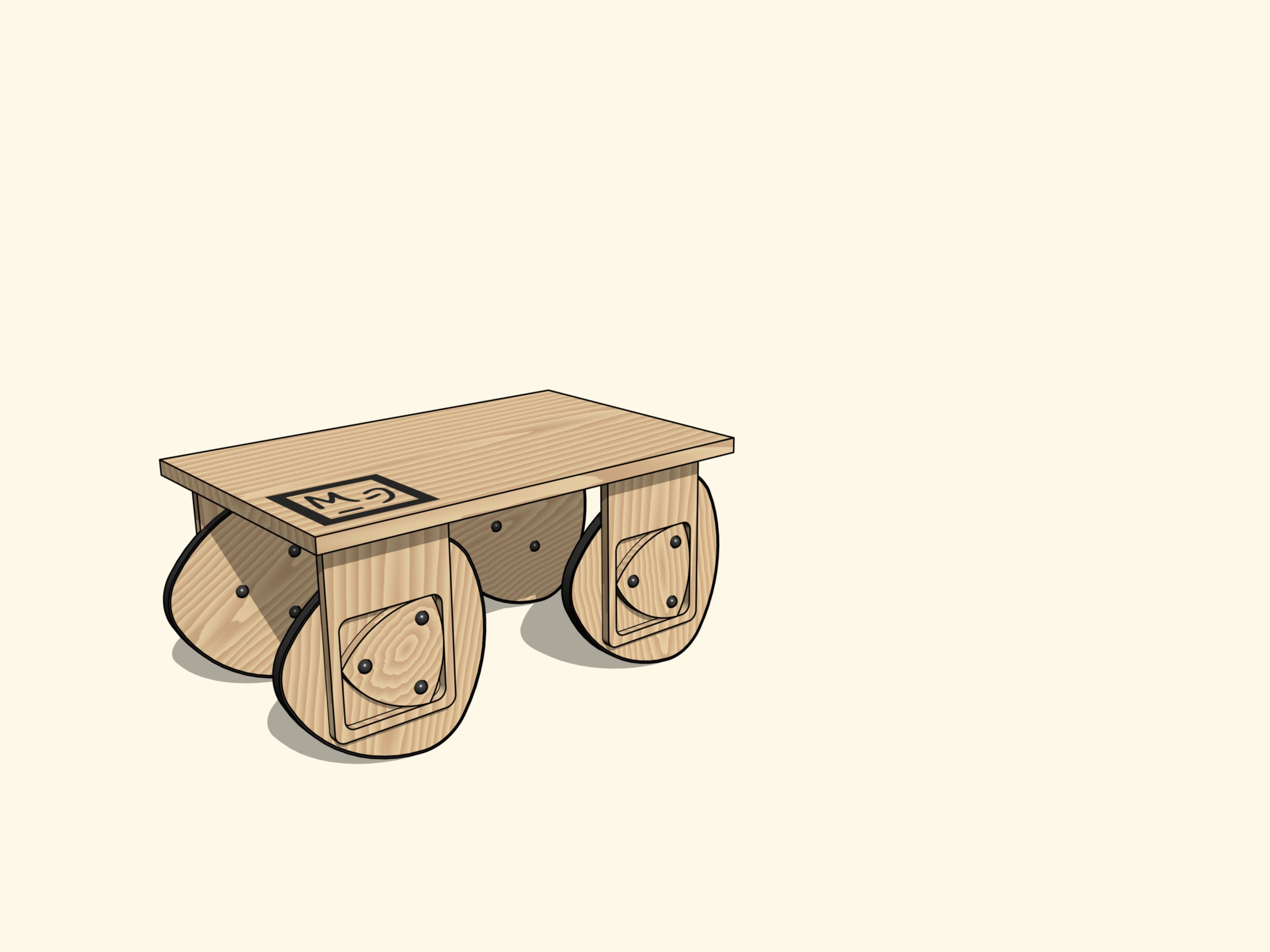
Значит, таким образом можно устроить подвеску некруглого колеса с краем в виде красной кривой.
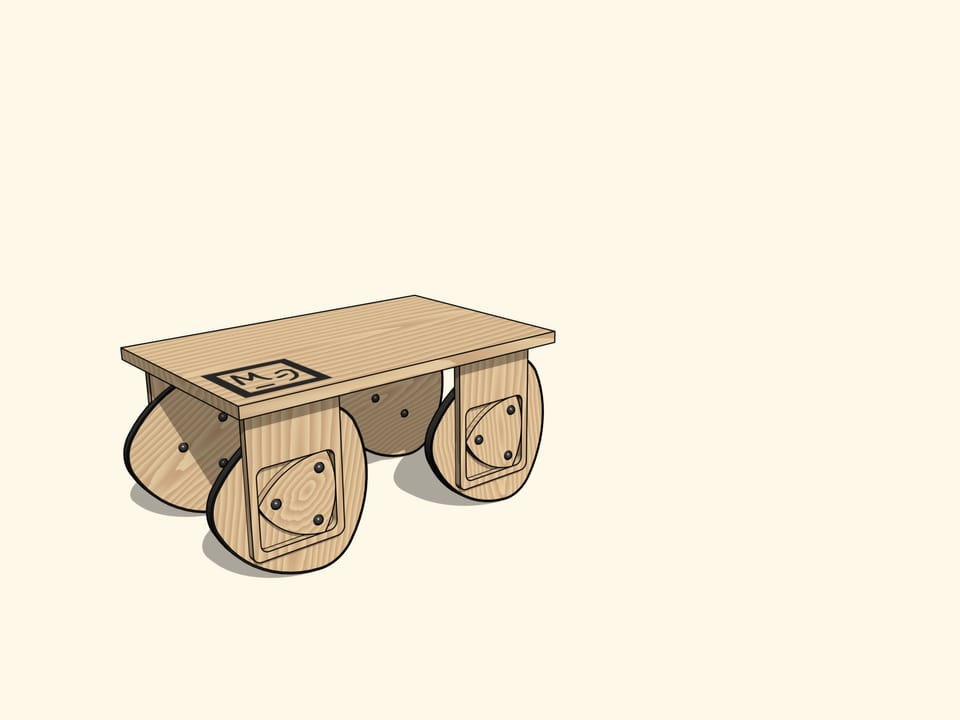
Взяв четыре таких подвески, можно соорудить повозку. При этом она будет ехать совершенно без покачиваний!
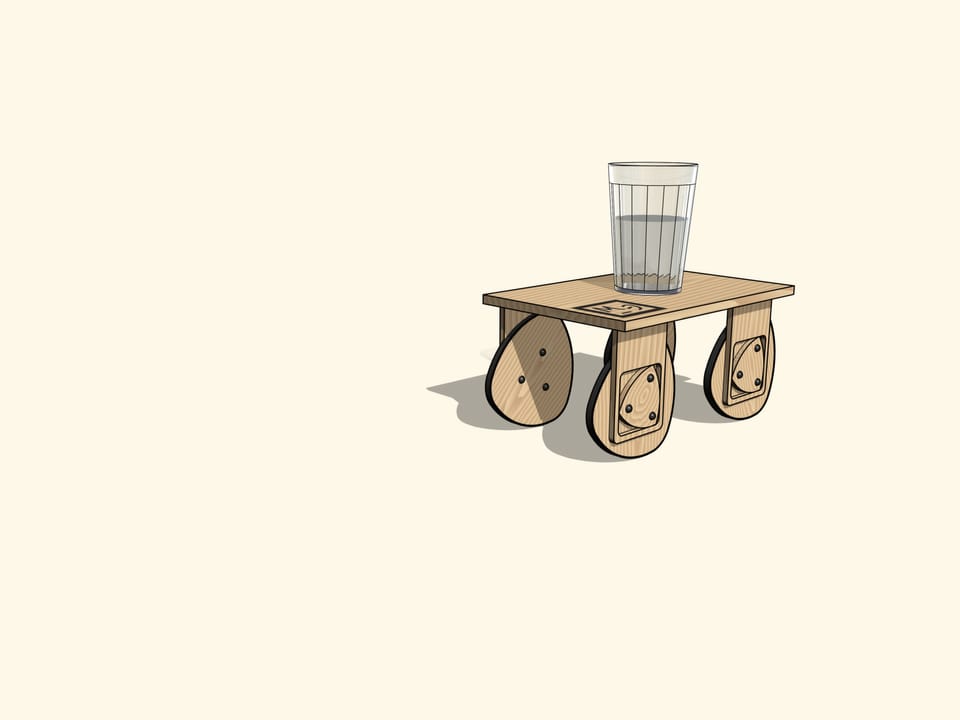
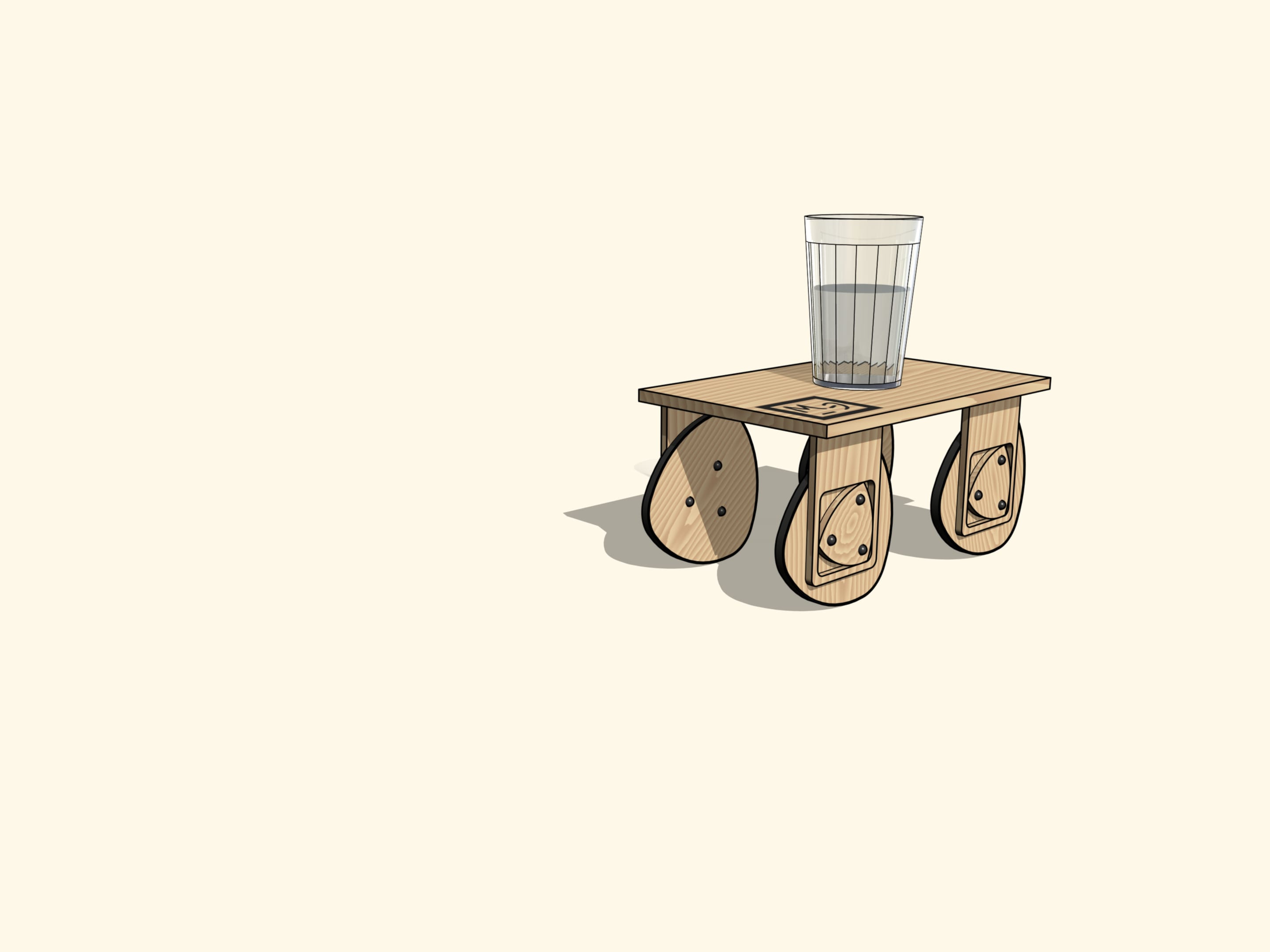
Дабы убедиться, что тряски нет, поставим, как учат автомобилистские традиции, на нашу тележку стакан с водой.
История того граненого стакана, к которому мы все привыкли, интересна. По всей видимости, его классический вид — количество граней, ободок сверху — придумала автор знаменитой скульптуры «Рабочий и колхозница» Вера Игнатьевна Мухина, выполняя заказ на создание сервиза для Кремля.
Гладкая поверхность воды нам еще раз покажет, что бывают некруглые колеса и способ их подвески, такие, что тележка на них будет ехать абсолютно ровно.
Смотри также
Фигуры постоянной ширины // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 84—85, 319—320.