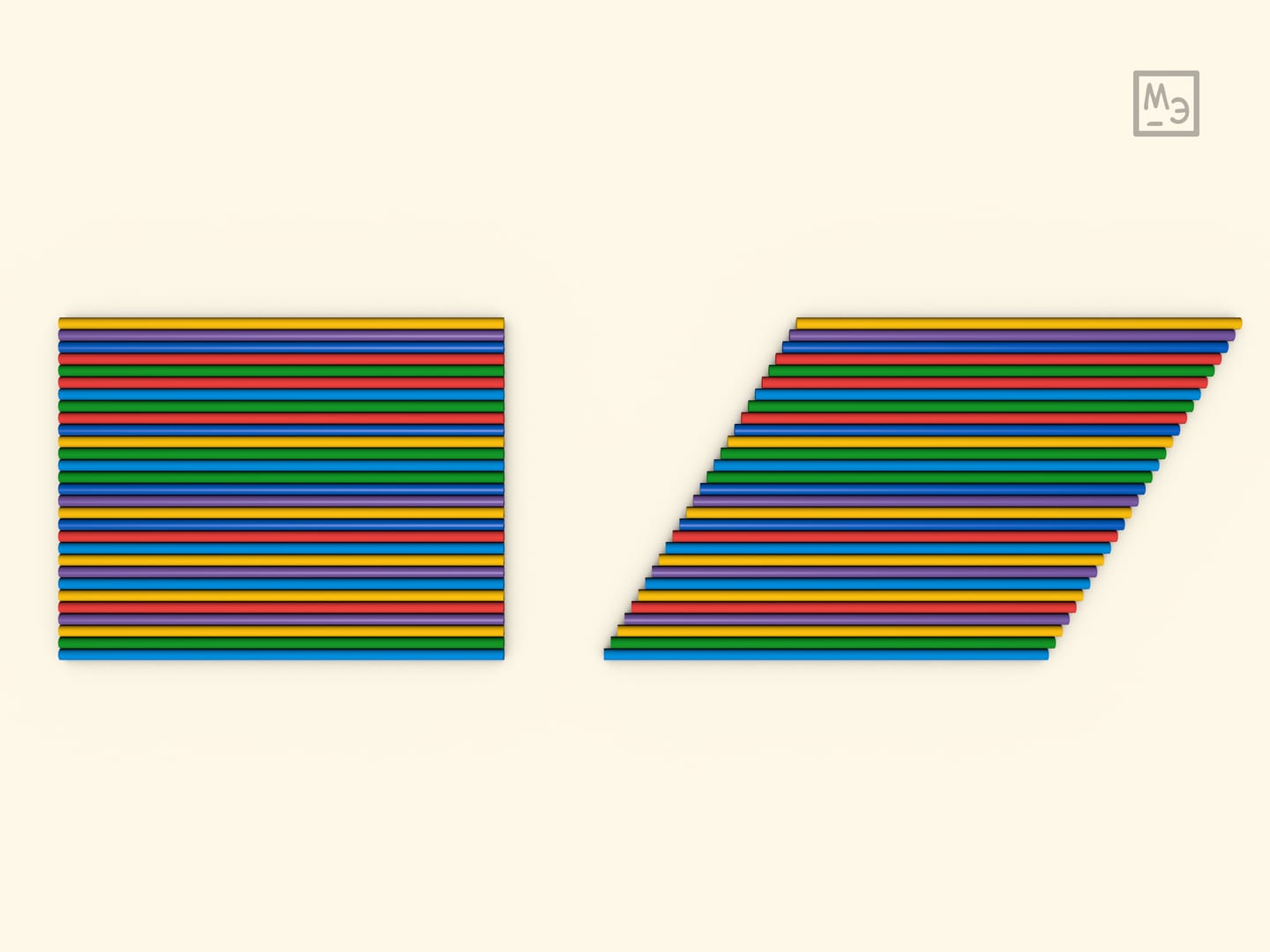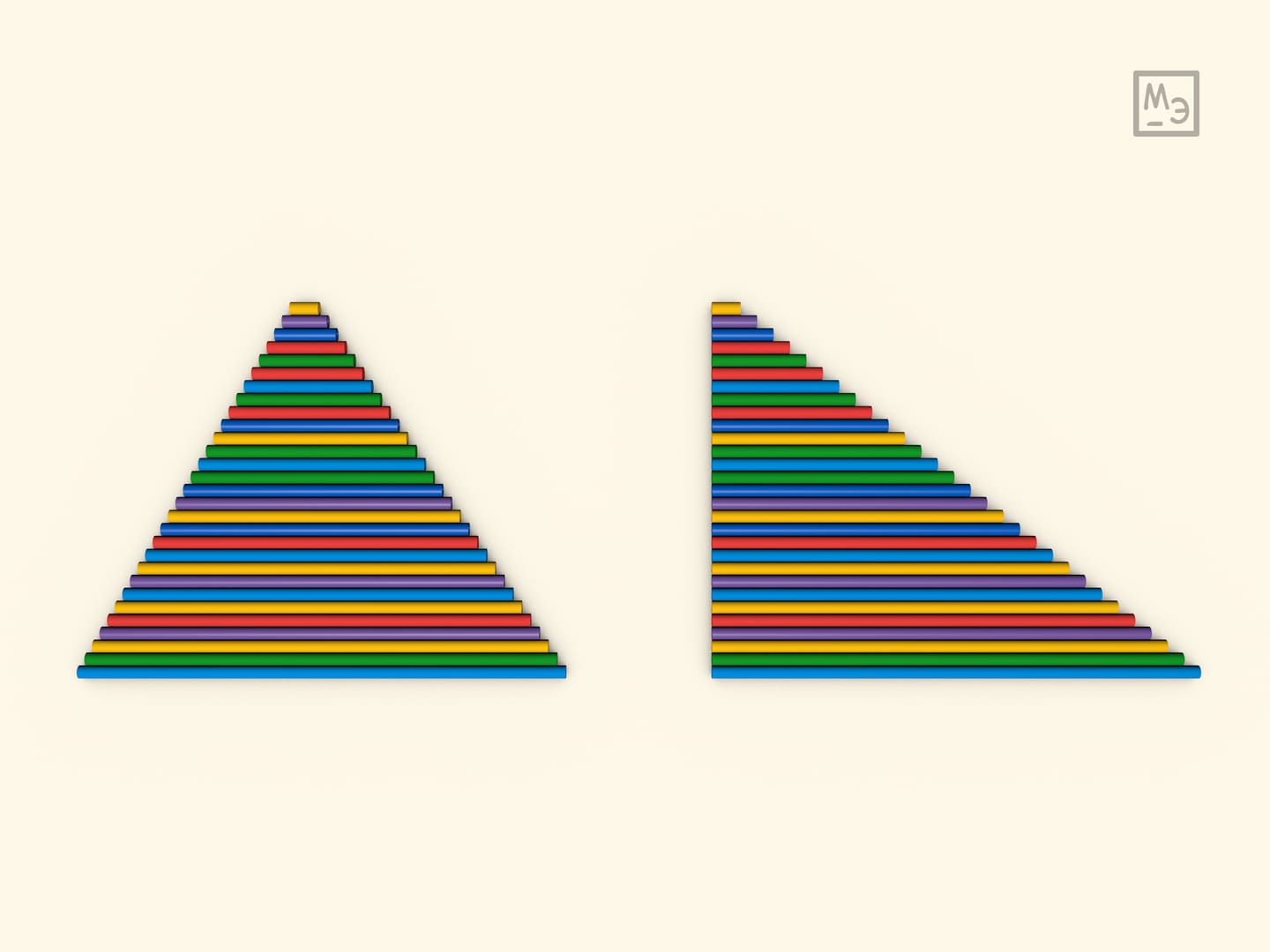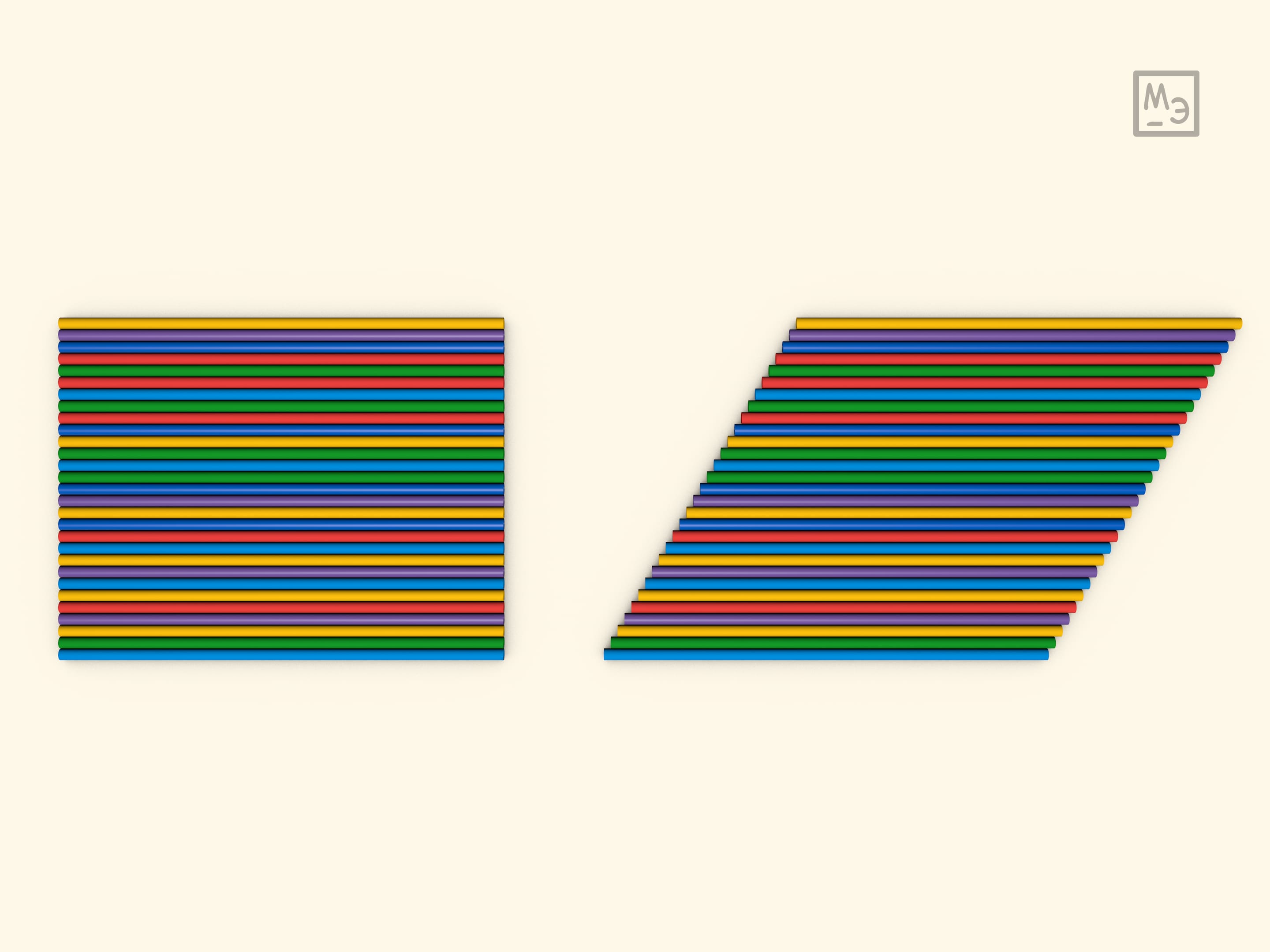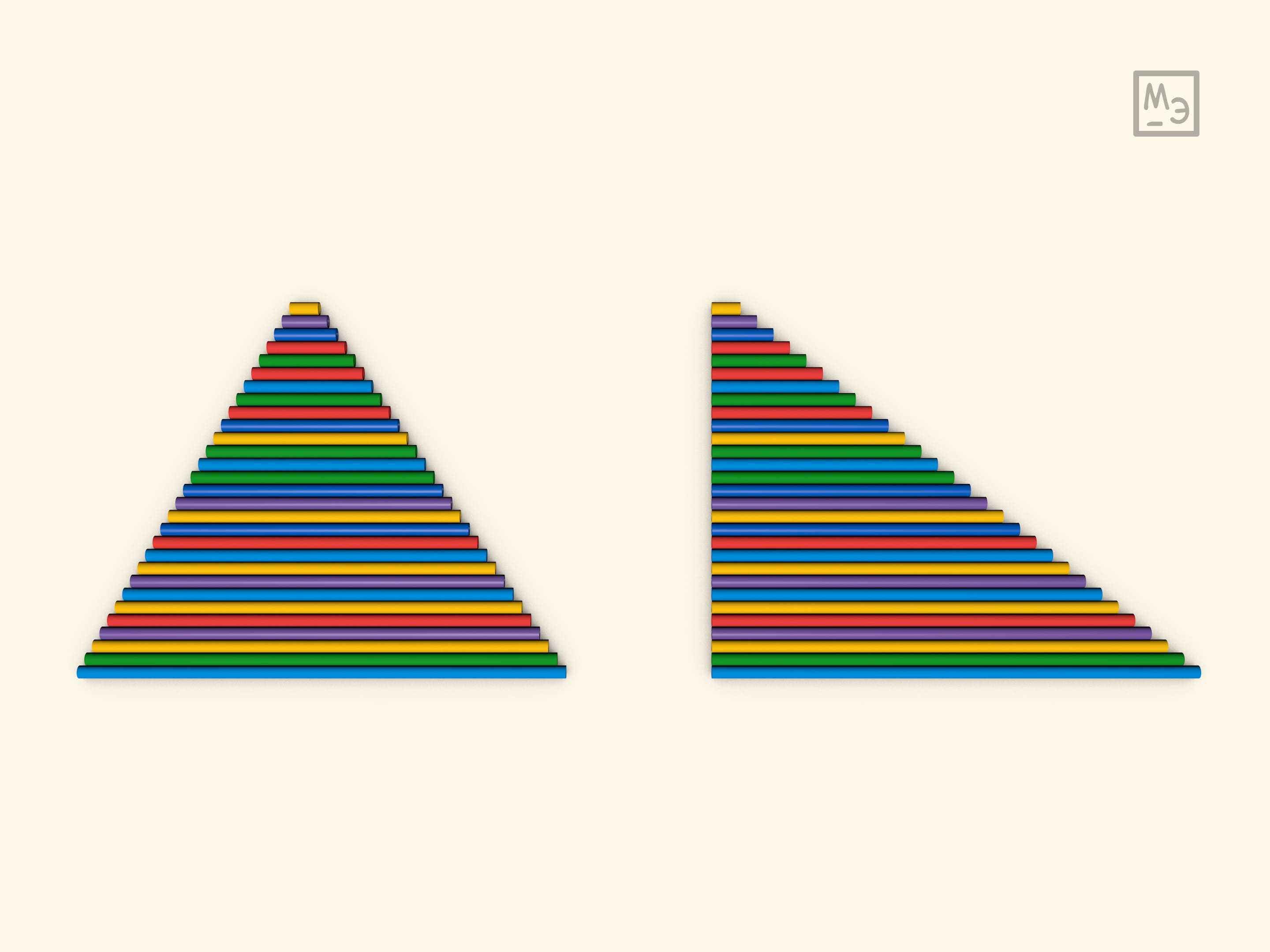Принцип Кавальери (итал. Bonaventura Francesco Cavalieri, лат. Cavalerius, 1598—1647) позволяет подсчитывать площади фигур и объёмы тел, сравнивая данные фигуры и тела с более простыми, площади и объёмы которых известны. Суть принципа Кавальери позволяет, как это и было в истории человечества, интуитивно подступиться к интегральному исчислению: представить площадь как сумму длин отрезков, а объём — как сумму площадей.
В случае фигур на плоскости для первого знакомства с принципом Кавальери можно использовать подставку под тарелки, сделанную по принципу плетёной циновки. В тех подставках, которые не обшиты по периметру тканью, отрезки могут сдвигаться друг относительно друга, оставаясь всегда параллельными. Во всех положениях площадь подставки остаётся одной и той же.
После первого знакомства на этой же модели полезно разобрать и парадокс, приведенный в письме Кавальери к Торричелли: ведь на самом деле при сдвиге циновки расстояние между отрезками меняется, а так можно «доказать» равенство площадей неравновеликих треугольников.
Другим удобным подспорьем для демонстрации принципа Кавальери могут стать трубочки для напитков. Их несложно обрезать, например, «под треугольник»; можно при желании соединить леской.
В трёхмерном пространстве принцип Кавальери можно продемонстрировать на одинаковых монетах или стопке одинаковых картонок (например, опять же, подставок под чашку/бокал). Если картонки круглые, то их можно сложить в цилиндр, если прямоугольные — в параллелепипед. В обоих случаях объём легко вычисляется. Тело, полученное сдвигом картонок относительно друг друга, выглядит более сложным, но объём его совпадает с объёмом исходного.
Бонавентура Кавальери в своём труде «Геометрия неделимых непрерывных, выведенная новым способом» (лат. Geometria indivisibilibus continuorum nova quadam ratione promota, 1635 год) дал теоретическое обоснование метода неделимых, использовавшегося и ранее. Так, Архимед по сути использовал метод неделимых при вычислении объёма шара, а Кеплер при формулировке законов движения планет рассуждал о площади как о сумме радиус-векторов. Одним из красивых применений принципа Кавальери на плоскости является подсчёт площади под циклоидой (лепестки Роберваля).