Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам. А центр вписанной в треугольник окружности лежит на пересечении биссектрис углов треугольника. И каждый раз приходится немного анализировать: кто, где… Простейшая модель из бумаги позволит запомнить, а заодно продемонстрировать два маленьких «чуда».
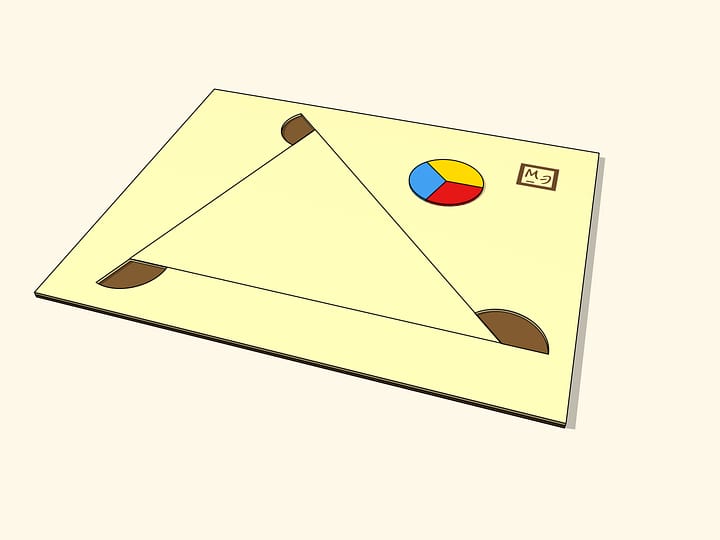
Вырежьте произвольный остроугольный треугольник из бумаги. Как найти середину его стороны и построить к ней серединный перпендикуляр? Да просто перегните листочек, совместите концы отрезка, середину которого строим, и от этой общей точки разгладьте сдвоенный листочек. Складка отметит и середину стороны, и серединный перпендикуляр к этой стороне.
Аккуратно проделав операцию со всеми тремя сторонами треугольника, можно продемонстрировать неподготовленному школьнику первое «чудо»: все три серединных перпендикуляра пересекутся в одной точке. В любом остроугольном треугольнике!
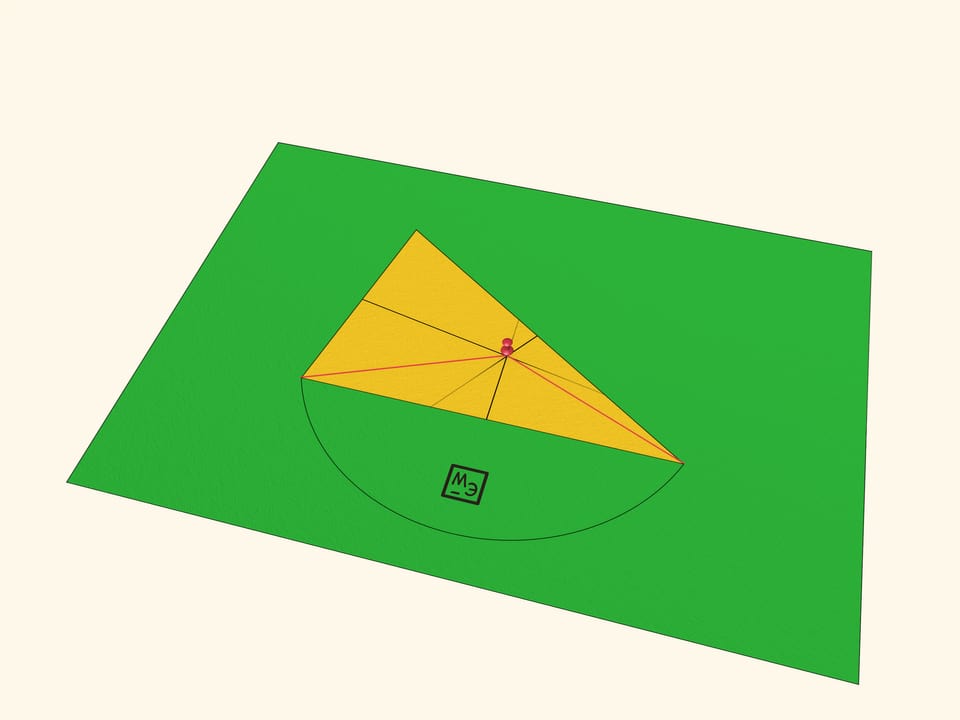
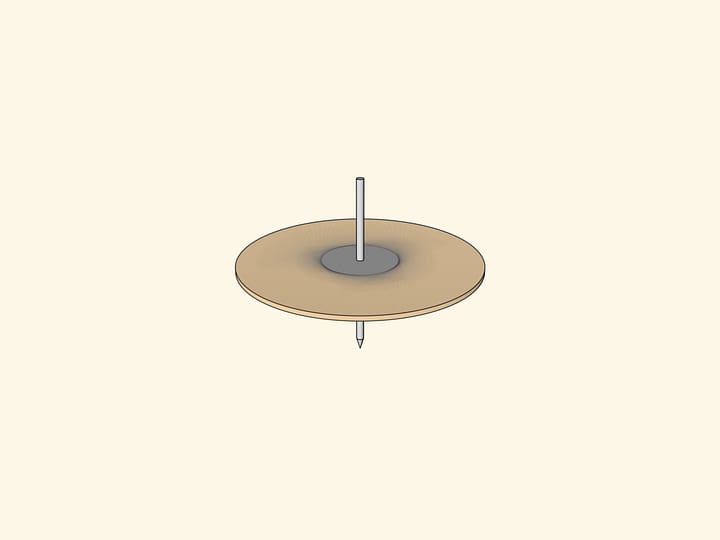
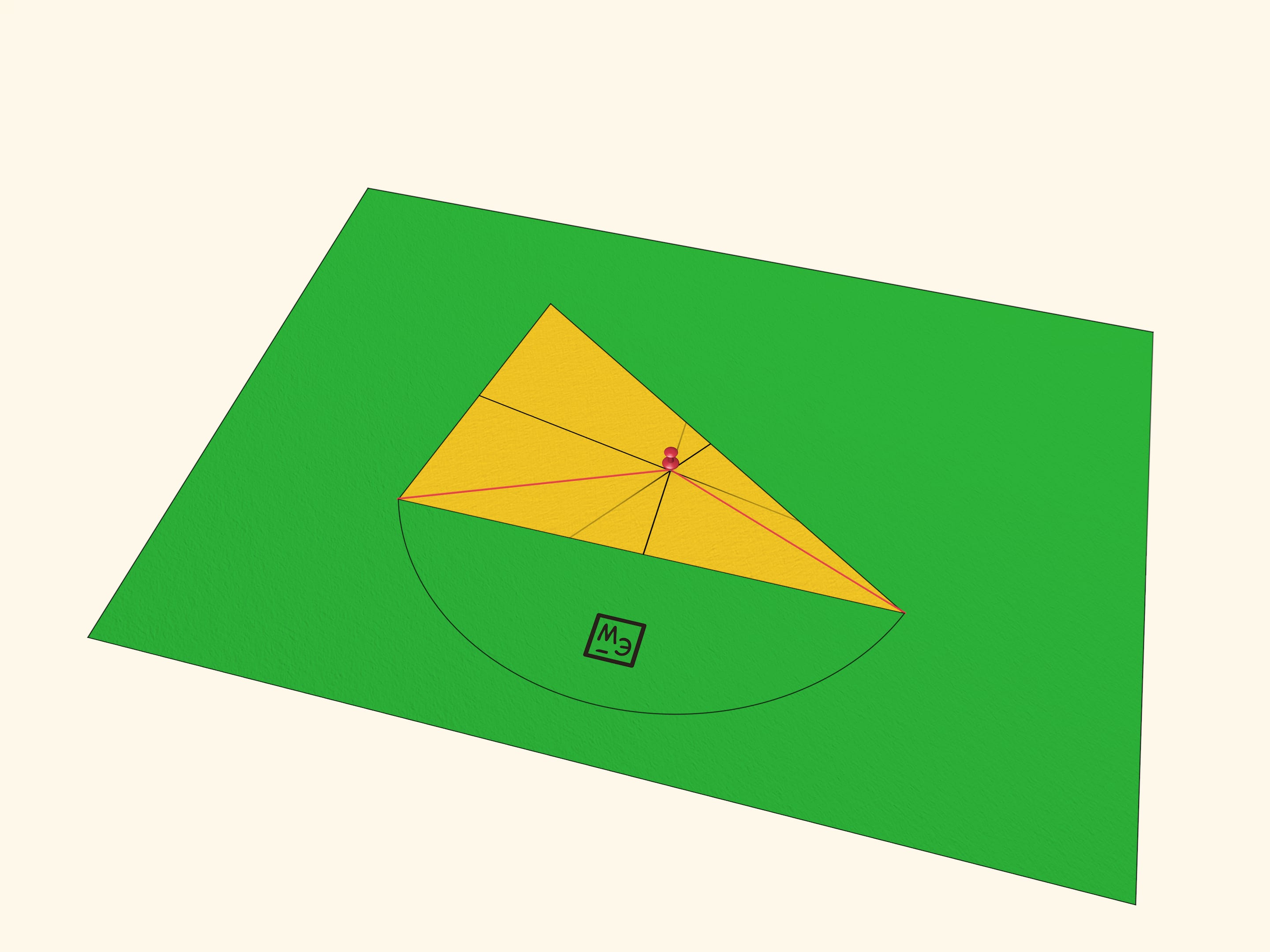
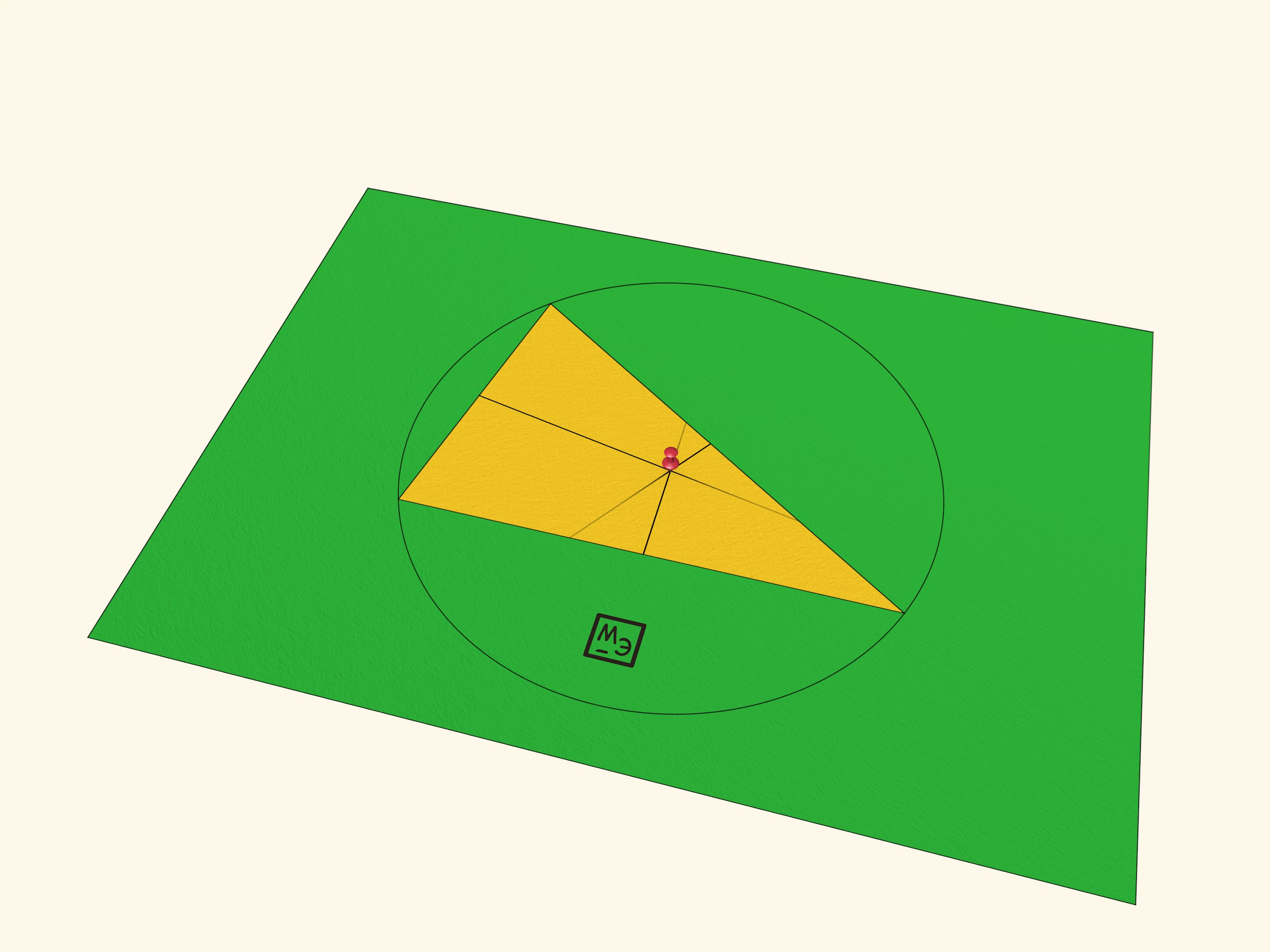
Приколите треугольник в точке пересечения серединных перпендикуляров к другому листу бумаги канцелярской кнопкой. С центром в этой точке и радиусом, равным расстоянию до одной из вершин, проведите окружность.
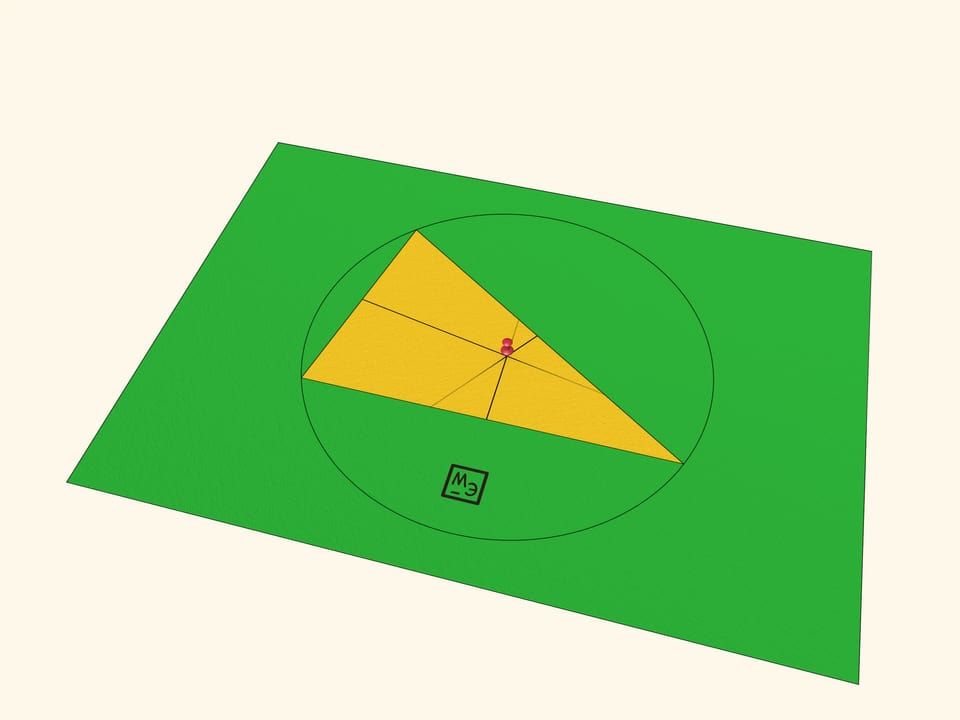
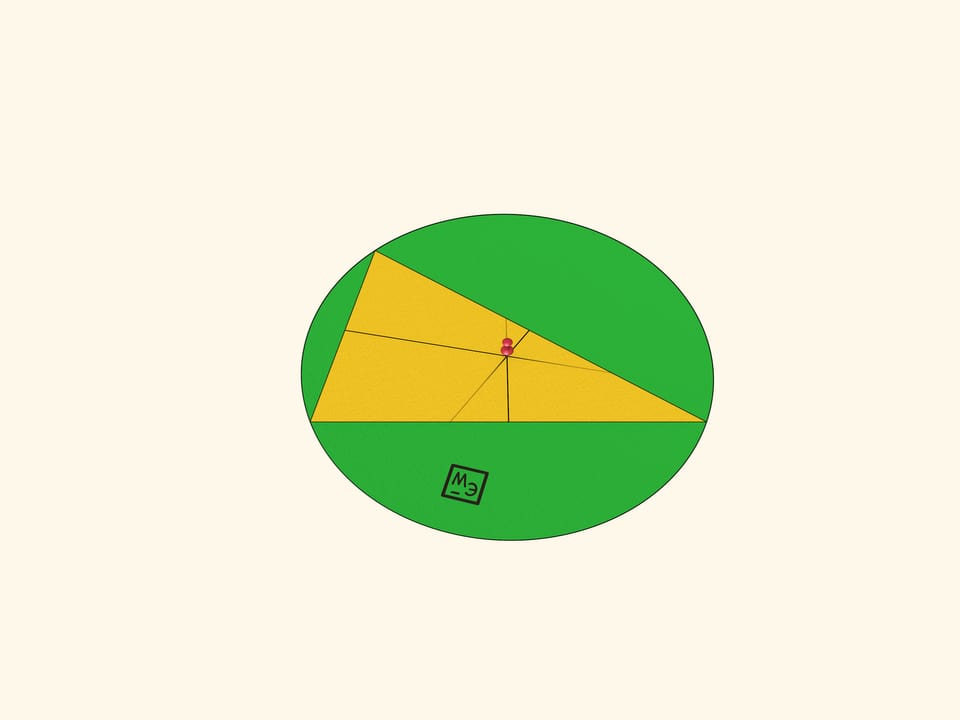
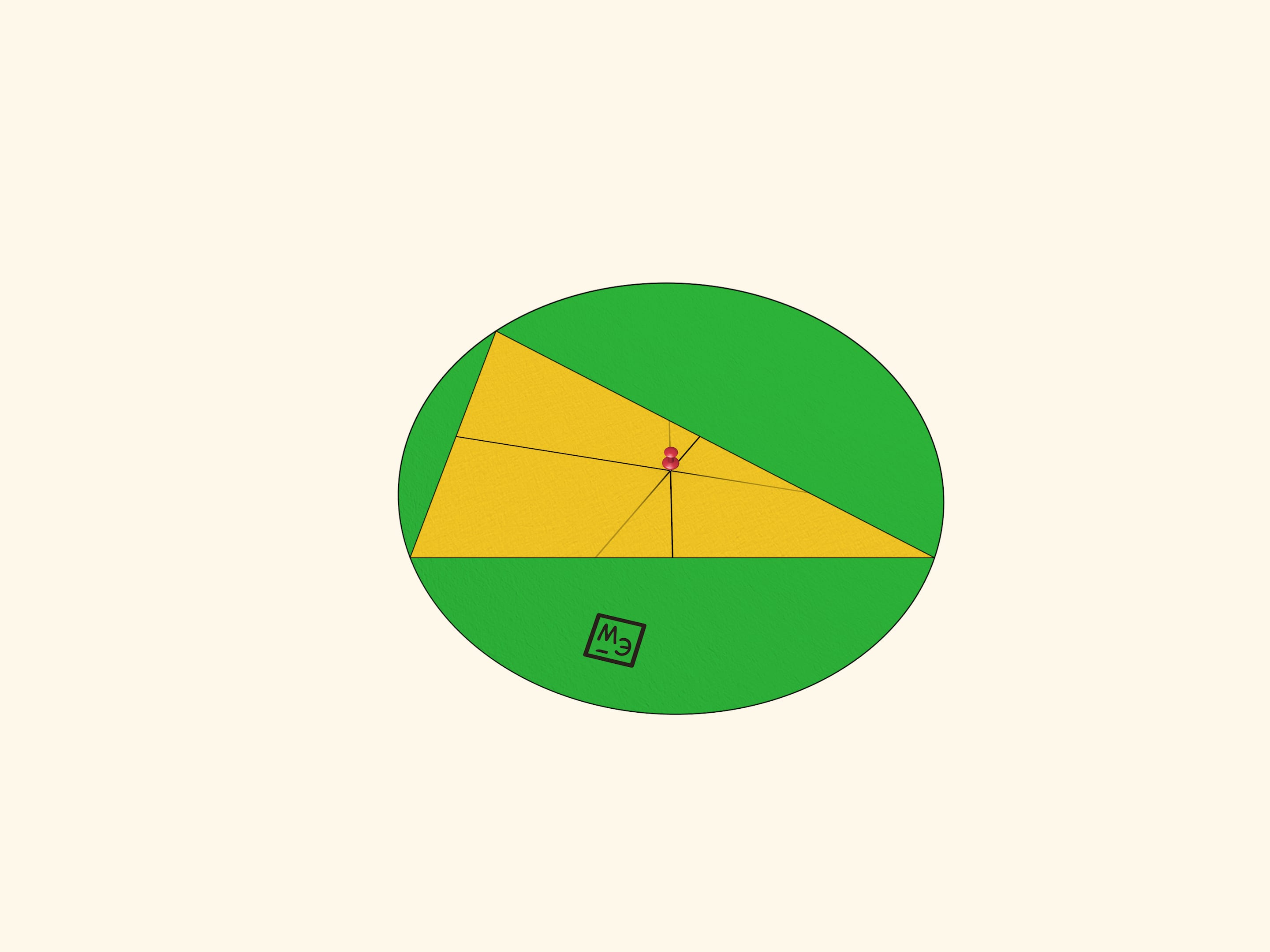
«Чудо» второе: все три вершины будут лежать на этой окружности. Доказательство элементарно: для каждой из сторон её вершины равноудалены от любой точки серединного перпендикуляра к ней, а точка пересечения всех трёх серединных перпендикуляров «обслуживает» все три стороны. Вырежьте круг: вращение треугольника на круге усиливает эффект «чуда».
Если провести произвольную хорду в окружности, то центр окружности будет лежать на серединном перпендикуляре к хорде. Отсюда и следует утверждение про описанную окружность треугольника. Из этого следует и утверждение про любой вписанный в окружность многоугольник: серединные перпендикуляры ко всем сторонам будут пересекаться в одной точке — центре описанной окружности.