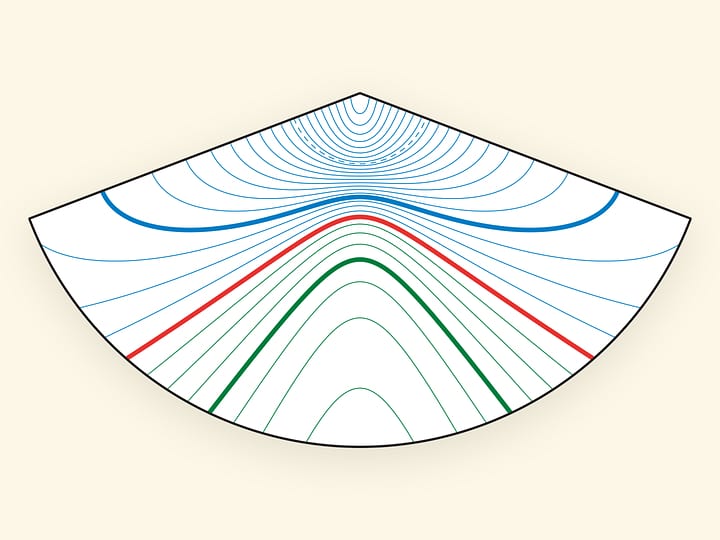
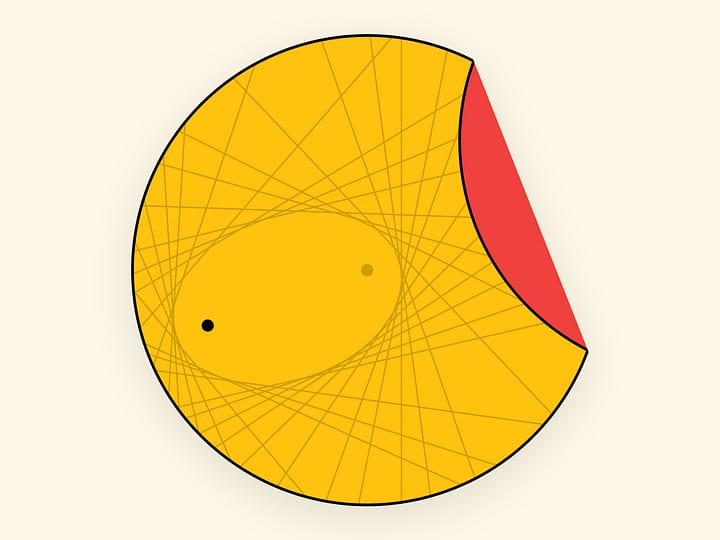
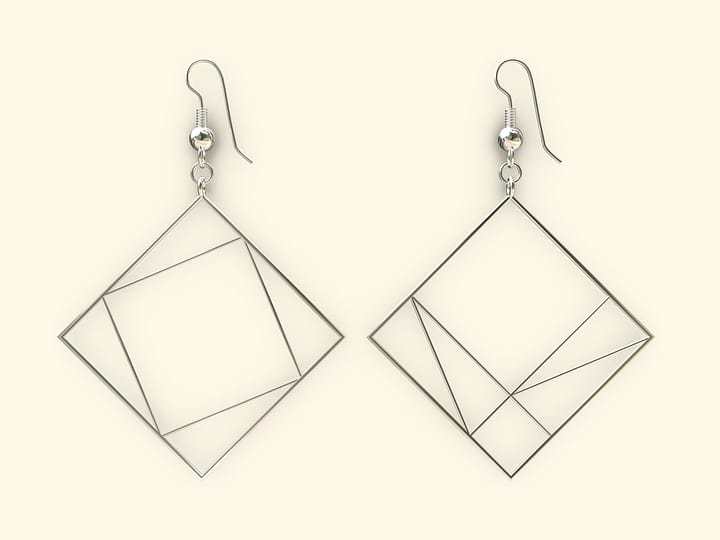
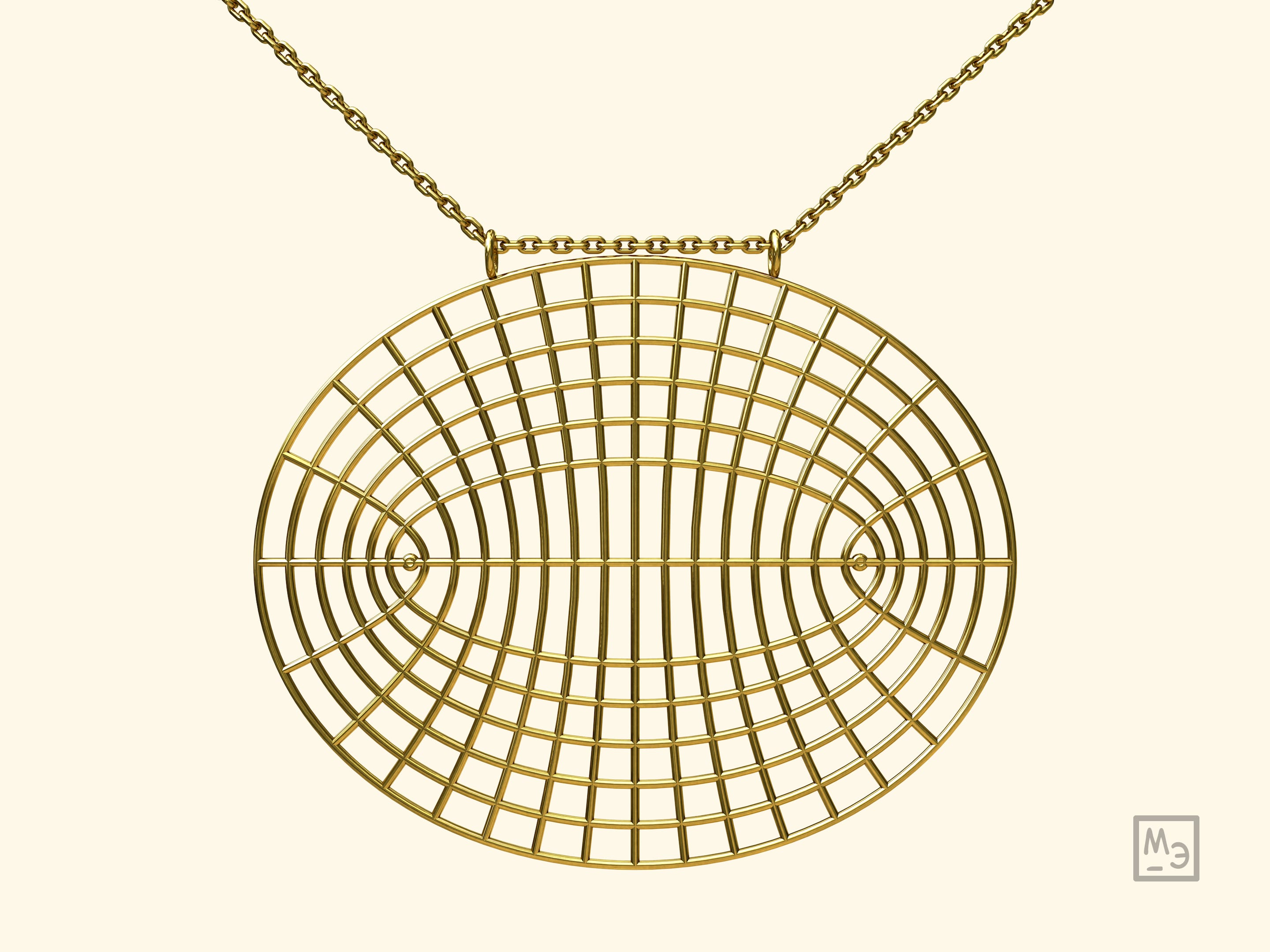
Софокусные эллипсы и гиперболы: кулон ⁠

Софо­кус­ные эллипсы и гипер­болы ⁠⁠перпен­ди­ку­лярны друг другу. (Углом между глад­кими кри­выми в точке их пере­се­че­ния назы­ва­ется угол между каса­тель­ными к кри­вым, про­ве­дён­ными в этой точке.) Пред­став­ляем кулон, в кото­рый заложены и матема­ти­че­ская кра­сота, и матема­ти­че­ская суть. Он поз­во­ляет обсу­дить, как выгля­дят семейство эллип­сов с дан­ными фоку­сами, семейство гипер­бол с теми же фоку­сами, и что любой эллипс перпен­ди­ку­ля­рен любой гипер­боле.

Перпен­ди­ку­ляр­ность софо­кус­ных эллип­сов и гипер­бол можно дока­зать геомет­ри­че­ски, исполь­зуя опти­че­ское свойство для точки их пере­се­че­ния. Для знающих комплекс­ный ана­лиз при­ве­дём ещё одно кра­си­вое дока­за­тельство.

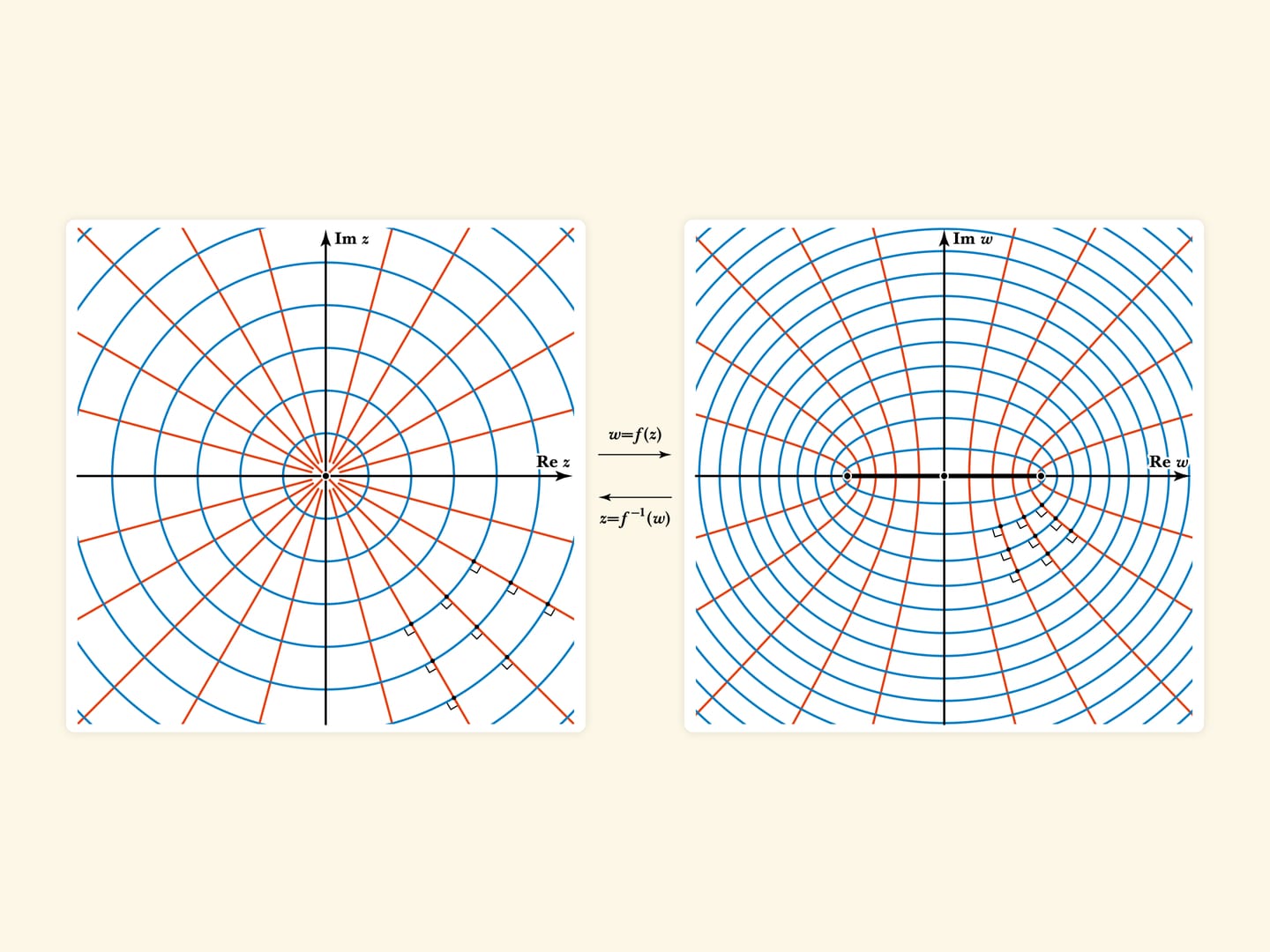
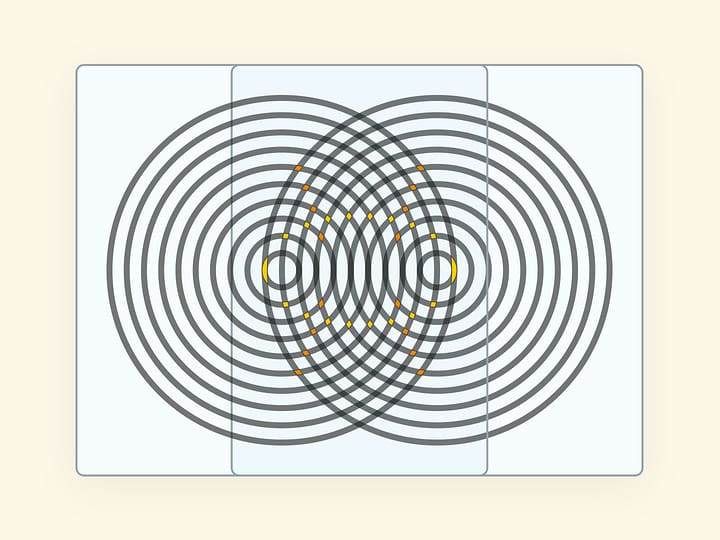
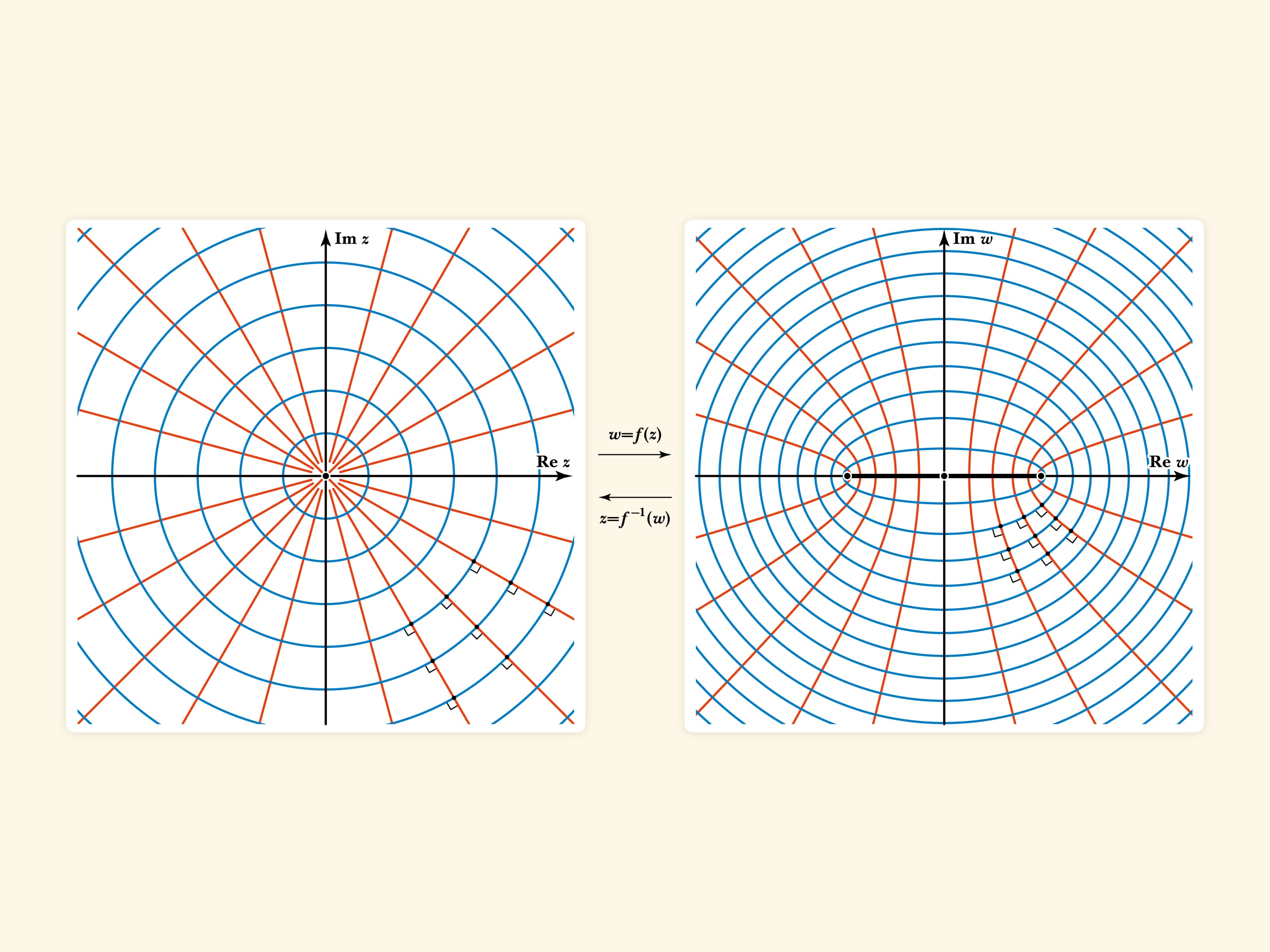
Знаме­ни­тая функция Нико­лая Его­ро­вича Жуков­ского $f(z)=\frac{1}{2}{\left(z+\frac{1}{z}\right)}$, исполь­зу­емая в зада­чах аэро­ди­намики, отоб­ражает поляр­ную сетку из окруж­но­стей с цен­тром в точке $z=0$ и их ради­у­сов на комплекс­ной плос­ко­сти в нашу кар­тинку! — софо­кус­ные эллипсы и гипер­болы с фоку­сами в точ­ках $\pm 1$. А функция Жуков­ского — конформ­ная (в обла­стях, не содержащих $\pm 1$): сохра­няет углы между кри­выми.