Конические сечения: муар⁠

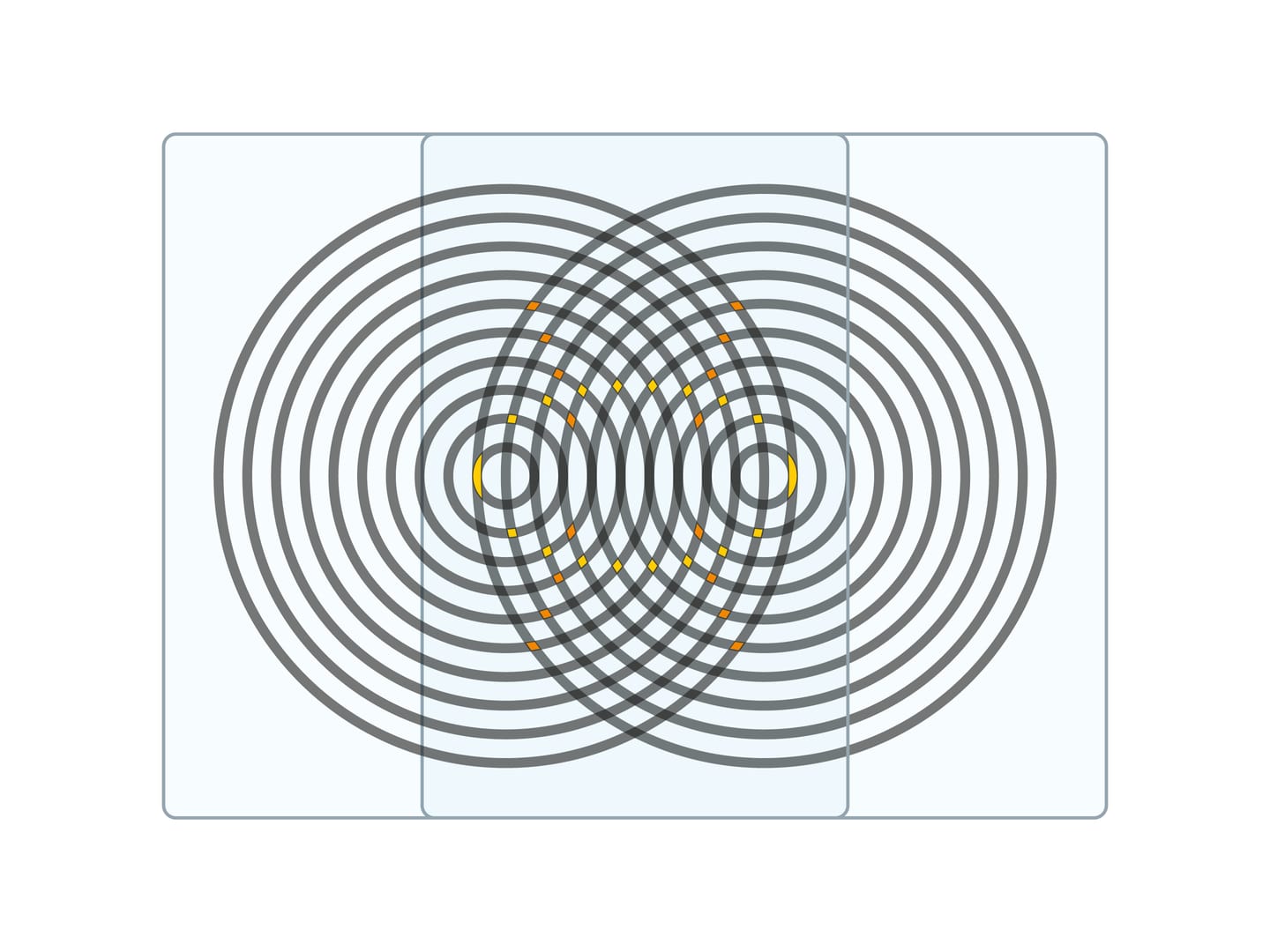
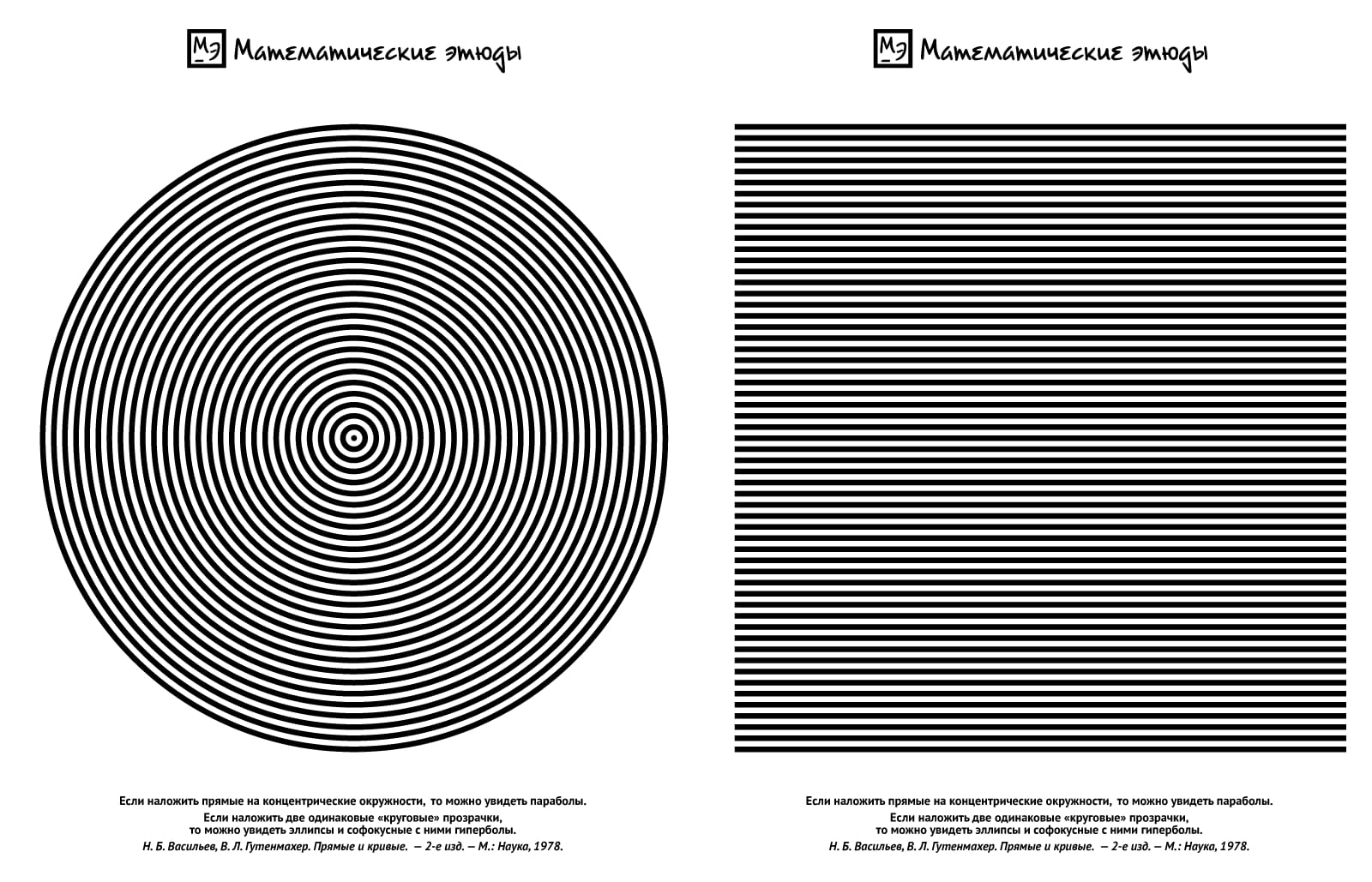
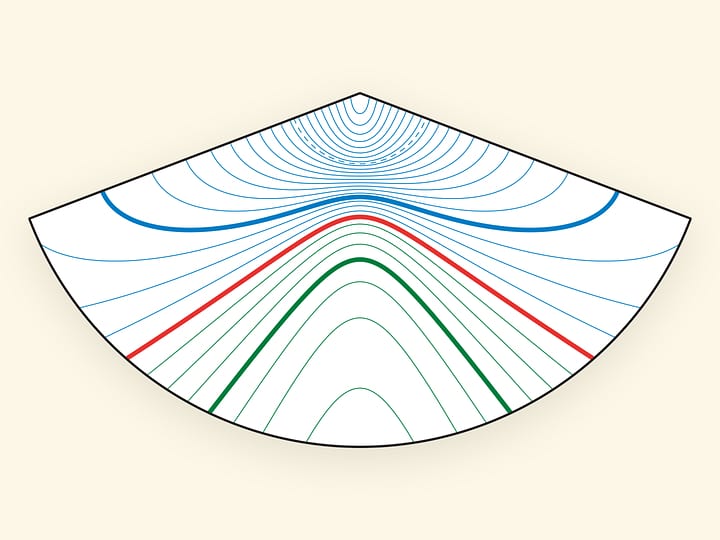
Все кони­че­ские сече­ния (эллипс, пара­болу, гипер­болу) можно полу­чить в виде муара — допол­ни­тель­ного геомет­ри­че­ского узора, обра­зующегося при наложе­нии двух изоб­раже­ний.

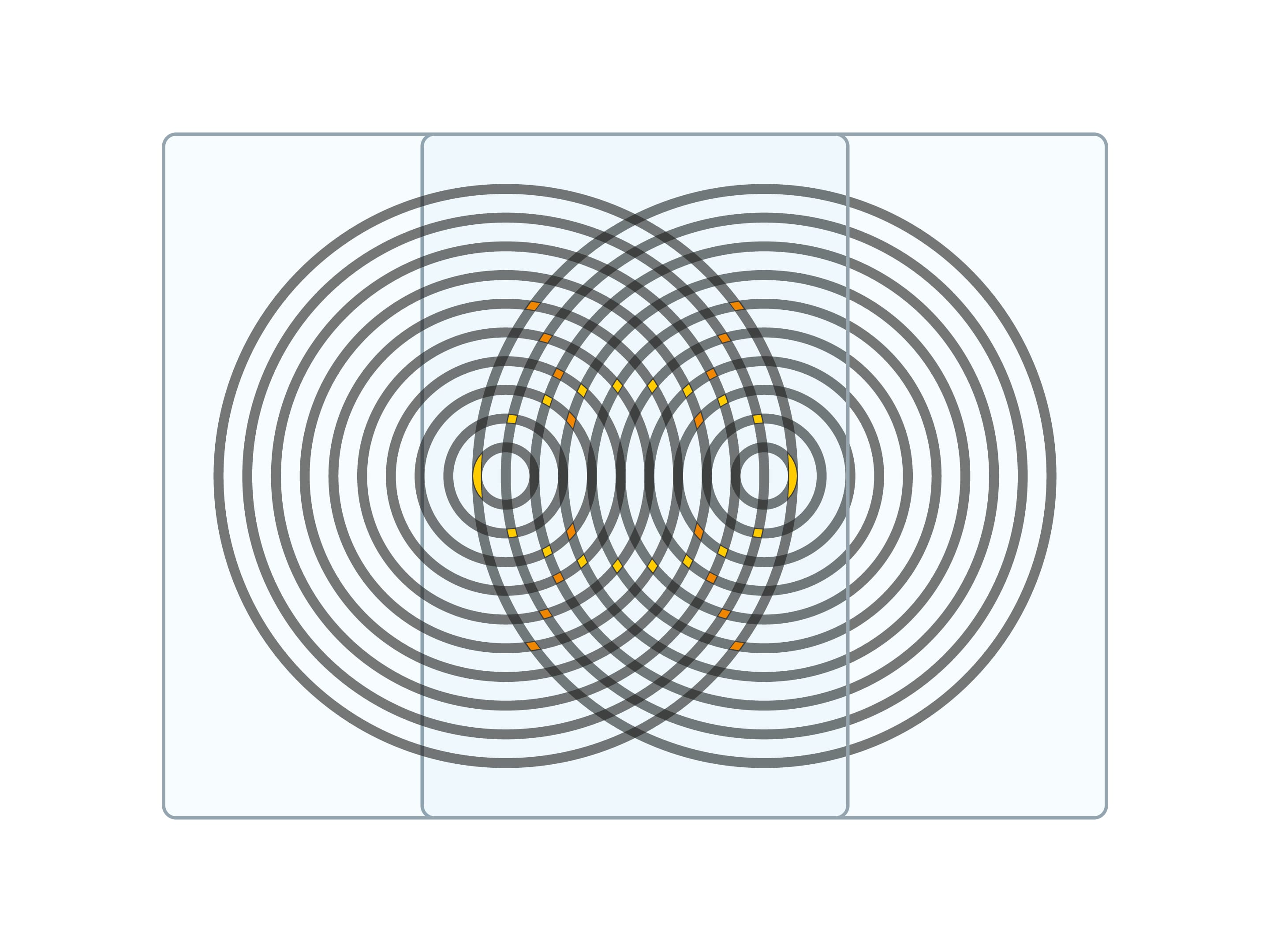
Возьмите «про­зрачку» и на прин­тере напе­ча­тайте прямо­ли­ней­ные полоски на фик­си­ро­ван­ном рас­сто­я­нии между сосед­ними. На другом листе напе­ча­тайте круго­вые полоски (концен­три­че­ские окруж­но­сти) той же ширины и с тем же рас­сто­я­нием между сосед­ними.

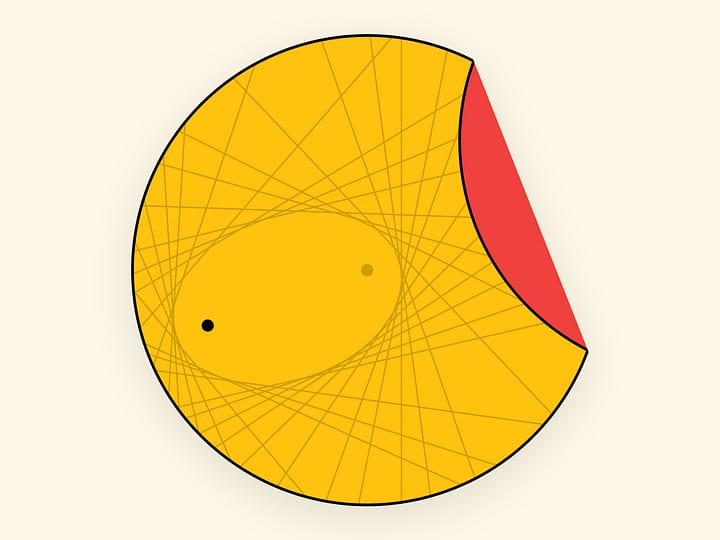
Если наложить прямые на концен­три­че­ские окруж­но­сти, то можно уви­деть семейство пара­бол. Каж­дая пара­бола — цепочка про­ти­вопо­лож­ных вершин кри­во­ли­ней­ных четырёх­уголь­ни­ков, огра­ни­чен­ных сосед­ними прямыми и сосед­ними окруж­но­стями. Сдвигая листы, можно и уви­деть изме­не­ние парамет­ров семейства пара­бол, и задуматься над положе­нием дирек­трисы и фокуса, исходя из опре­де­ле­ния пара­болы.

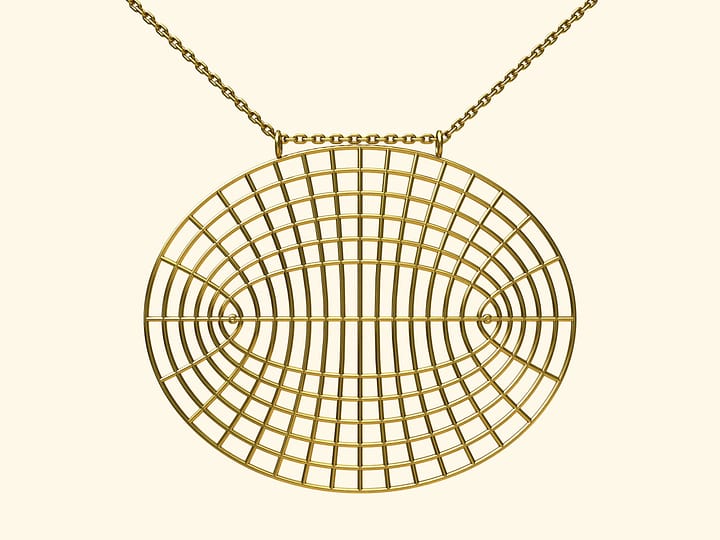
А если наложить две оди­на­ко­вые «круго­вые» про­зрачки, то можно уви­деть эллипсы и пере­се­кающие их гипер­болы с общими фоку­сами — цен­трами окруж­но­стей. И в этом слу­чае шеве­ле­ние про­зра­чек поможет и обна­ружить эти линии, и про­сле­дить за изме­не­нием парамет­ров кри­вых.