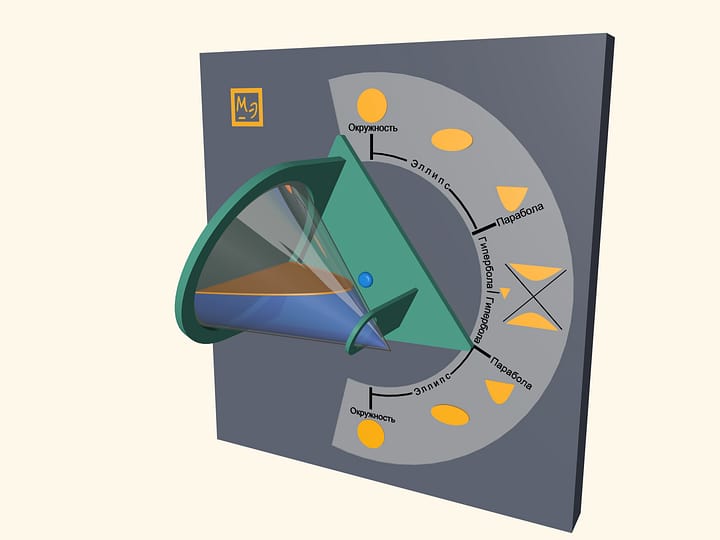
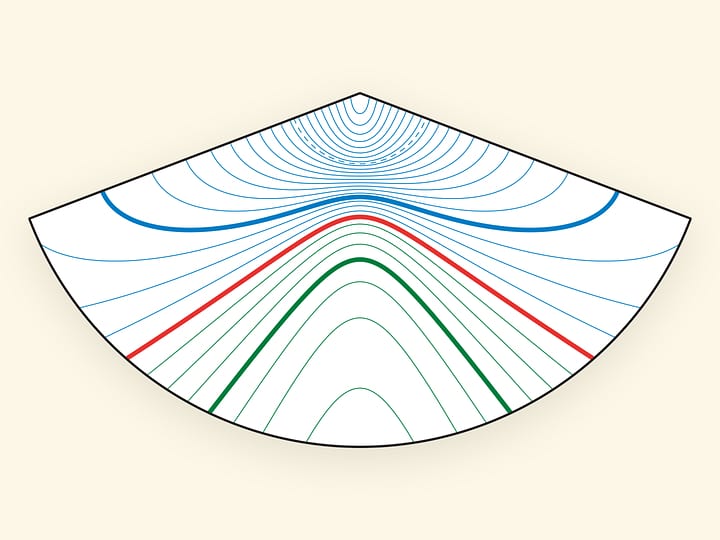
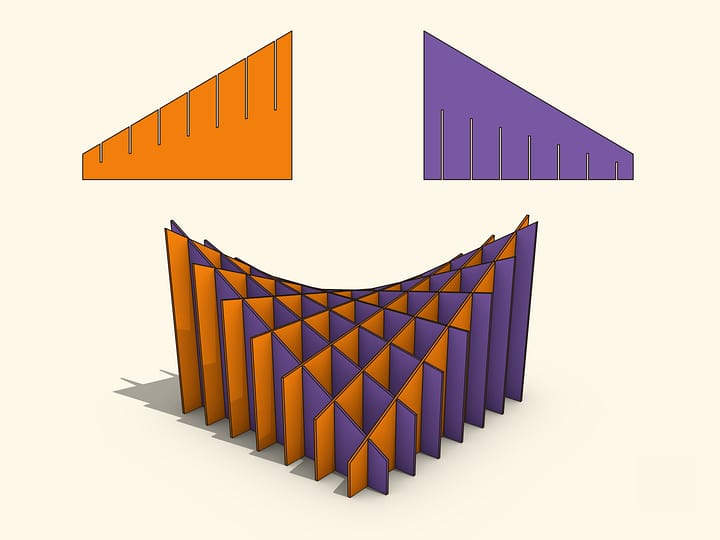
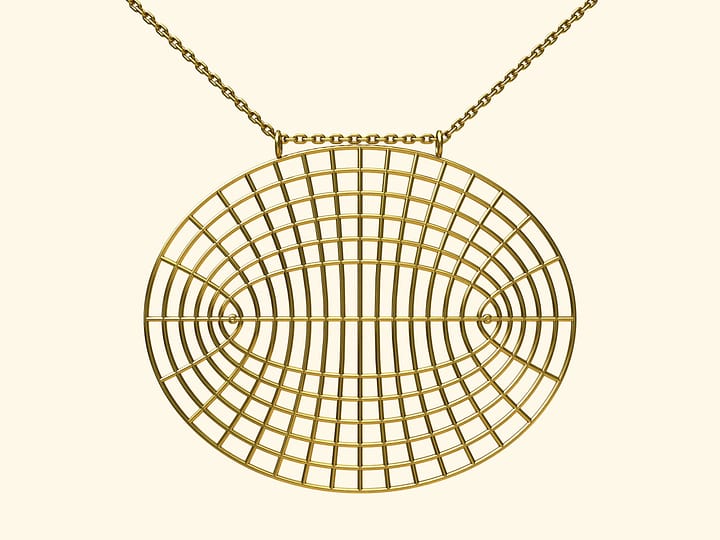
Простейшая модель, демонстрирующая нетривиальные конические сечения: эллипс, параболу, гиперболу. Опыт показывает, что далеко не все правильно отвечают на вопрос какое из нижних сечений парабола, а какое гипербола.
Для ответа на этот вопрос стоит нарисовать, например, графики функций $y=x^2$ и $y=1/x$ и посмотреть на параболу и гиперболу. Следующий шаг — вспомнить определение прямого кругового конуса: поверхность, образованная вращением прямой вокруг пересекающейся с ней оси. Это определение напоминает, что у конуса две полы, и, значит, если плоскость одного из этих сечений пересекает обе половины, то высекает гиперболу, а если только одну, то параболу.
Другие модели раздела «Конические сечения»
