Простые числа — те, которые нельзя представить в виде произведения двух меньших. Простые числа являются «кирпичиками» из которых составлены все остальные числа.
Греческий учёный Эратосфен в III веке до н. э. придумал способ, алгоритм нахождения всех простых чисел, не превосходящих некоторого фиксированного числа $N$. Выпишем все натуральные числа от $2$ до $N$. Вычеркнем в списке все числа, кратные $2$ (кроме самой двойки); наименьшее невычеркнутое число после $2$ — это $3$, следующее простое число. Оставляем тройку и вычёркиваем числа, кратные $3$, и т. д. Если такие действия проделать для всех чисел, не превосходящих $\sqrt{N}$, то незачёркнутыми останутся все простые числа и только они.
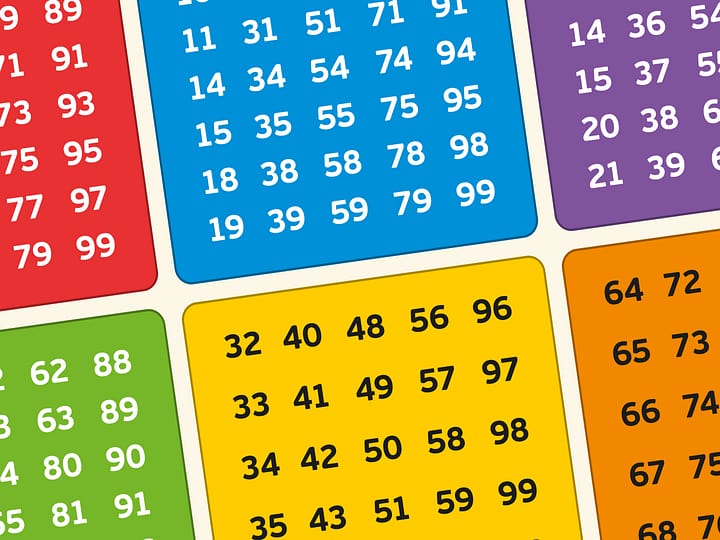
Описанный процесс можно механизировать, сделать наглядным. Напечатайте на листе бумаги числа от $1$ до $N=nm$ в виде таблицы размера $n\times m$. На первой прозрачке на местах чётных чисел (кроме $2$) напечатайте закрашенные области. На второй — то же с числами, кратными $3$ (кроме самой тройки), и т. д. Если создать достаточно большой набор таких прозрачек, то при наложении их на основную таблицу все простые числа будут видны (пройдут через сито, решето отбора), а все составные — скрыты.
На каждом листе-прозрачке закрашенные клетки будут встречаться через одинаковое число шагов, а вот вид и расположение образуемых ими линий зависят от количества столбцов в таблице.
Решето Эратосфена можно реализовать различными способами, в том числе и «механически». Одну идею подсказывает само название: листы-подложки поддерживают шары, а вынимание очередного листа приводит к падению шаров, «кратных» соответствующему числу.
При изготовлении модели самостоятельно стоит подумать над тем, какое максимальное число стоит взять при задуманном числе «шагов» алгоритма и поэкспериментировать с представлением соответствующего отрезка натурального ряда в виде таблицы.
Литература
Периодические цикады // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 79, 318—319.