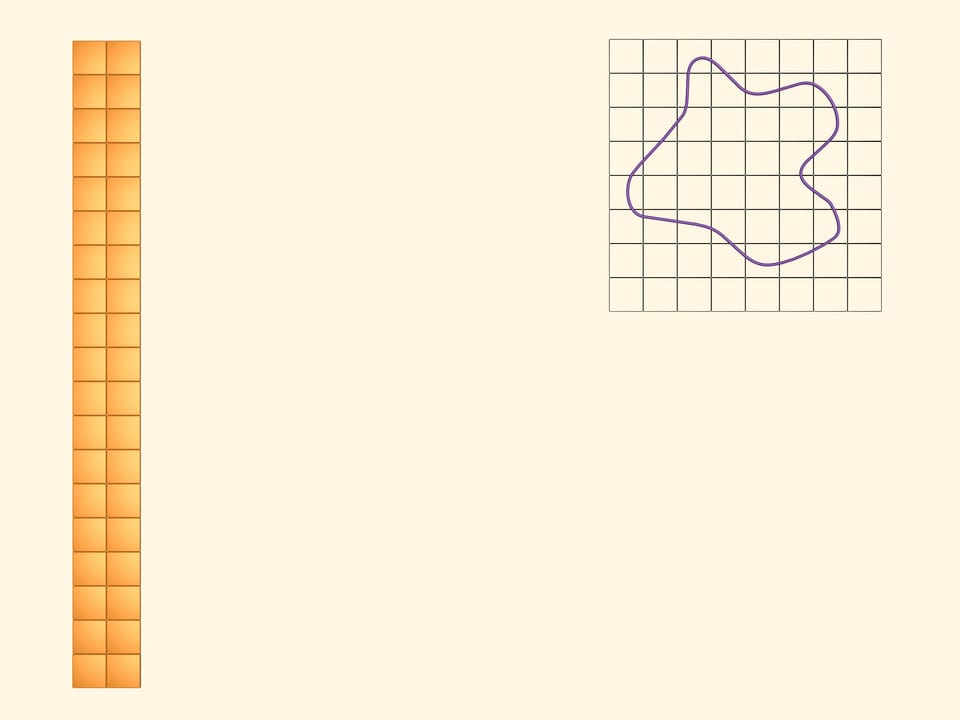
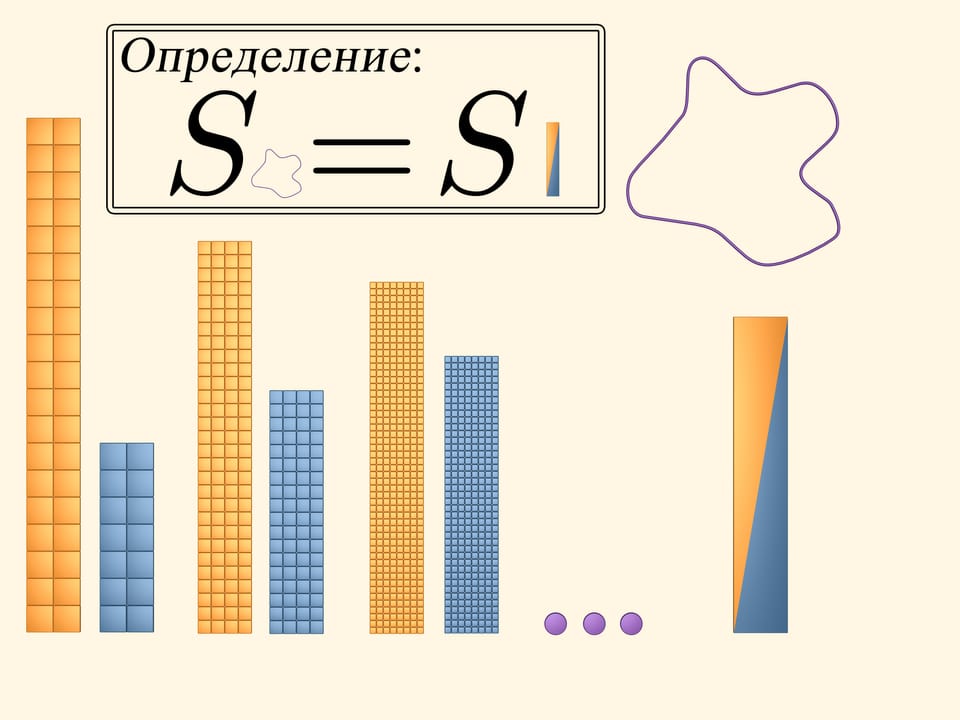
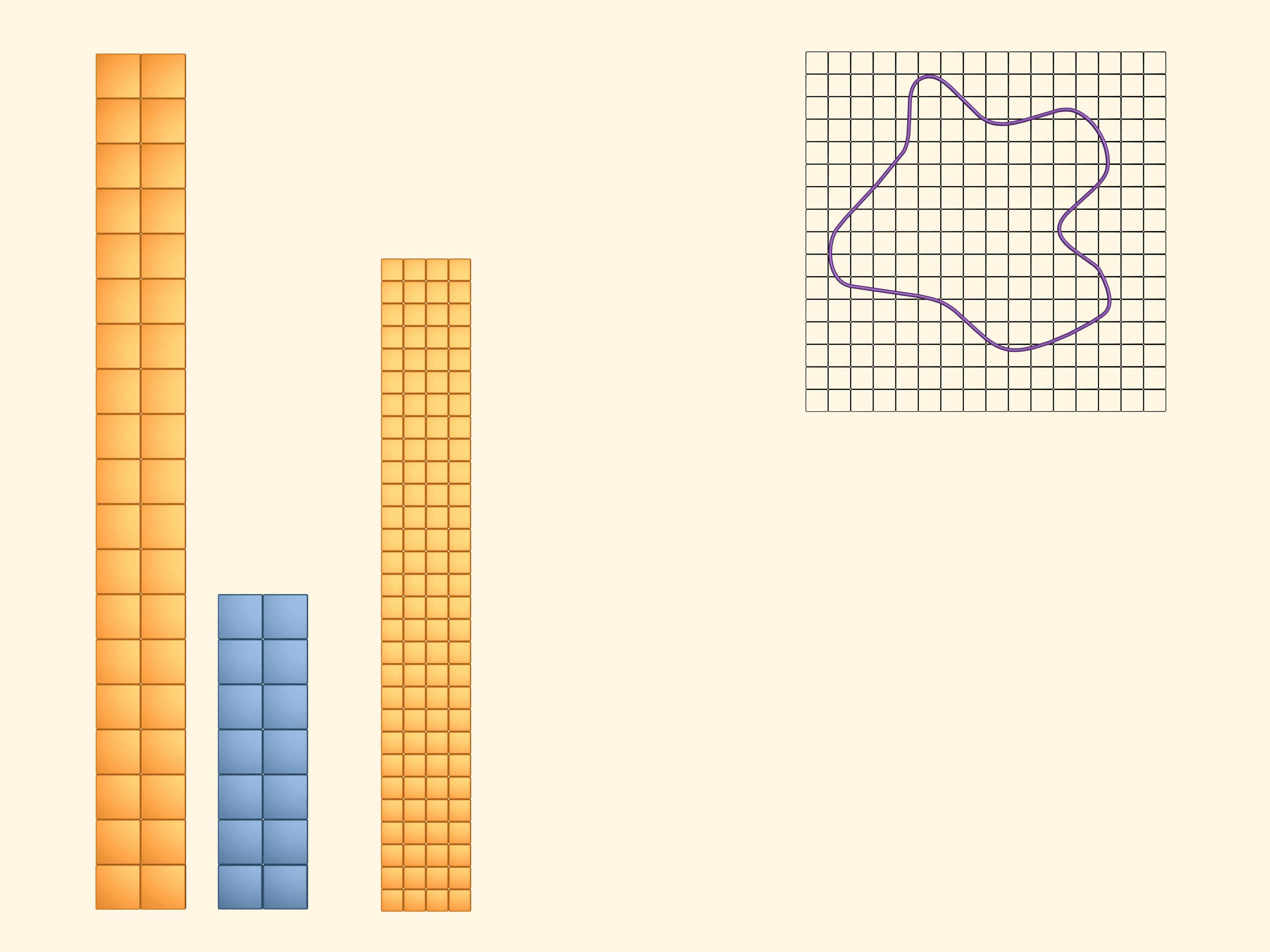Площадь квадрата равна квадрату длины его стороны. Легко посчитать площадь фигуры, разбивающейся на несколько квадратов. А чему равна площадь фигуры, ограниченной произвольной кривой?
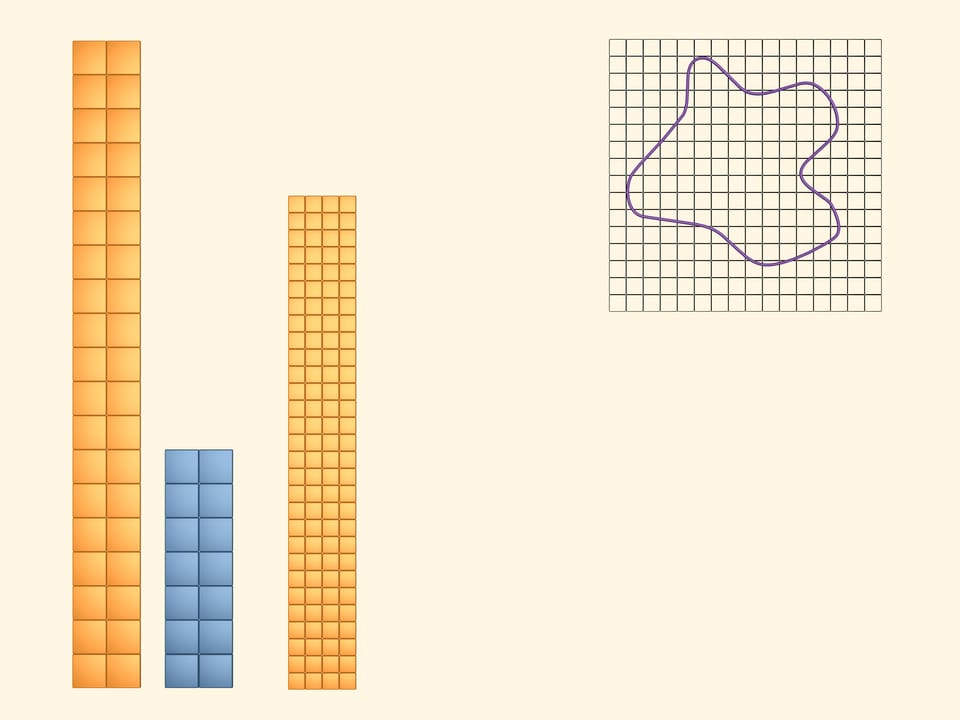
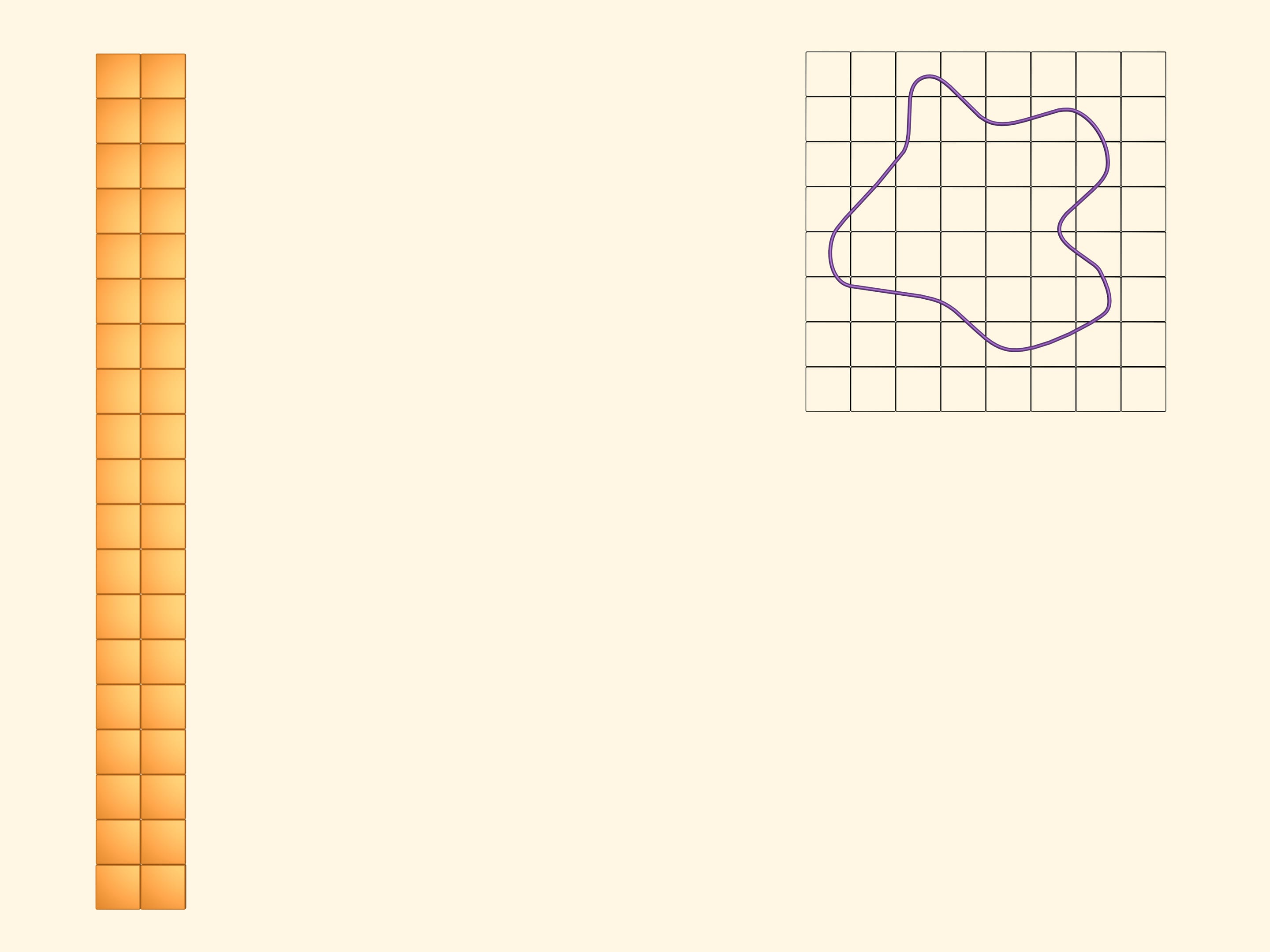
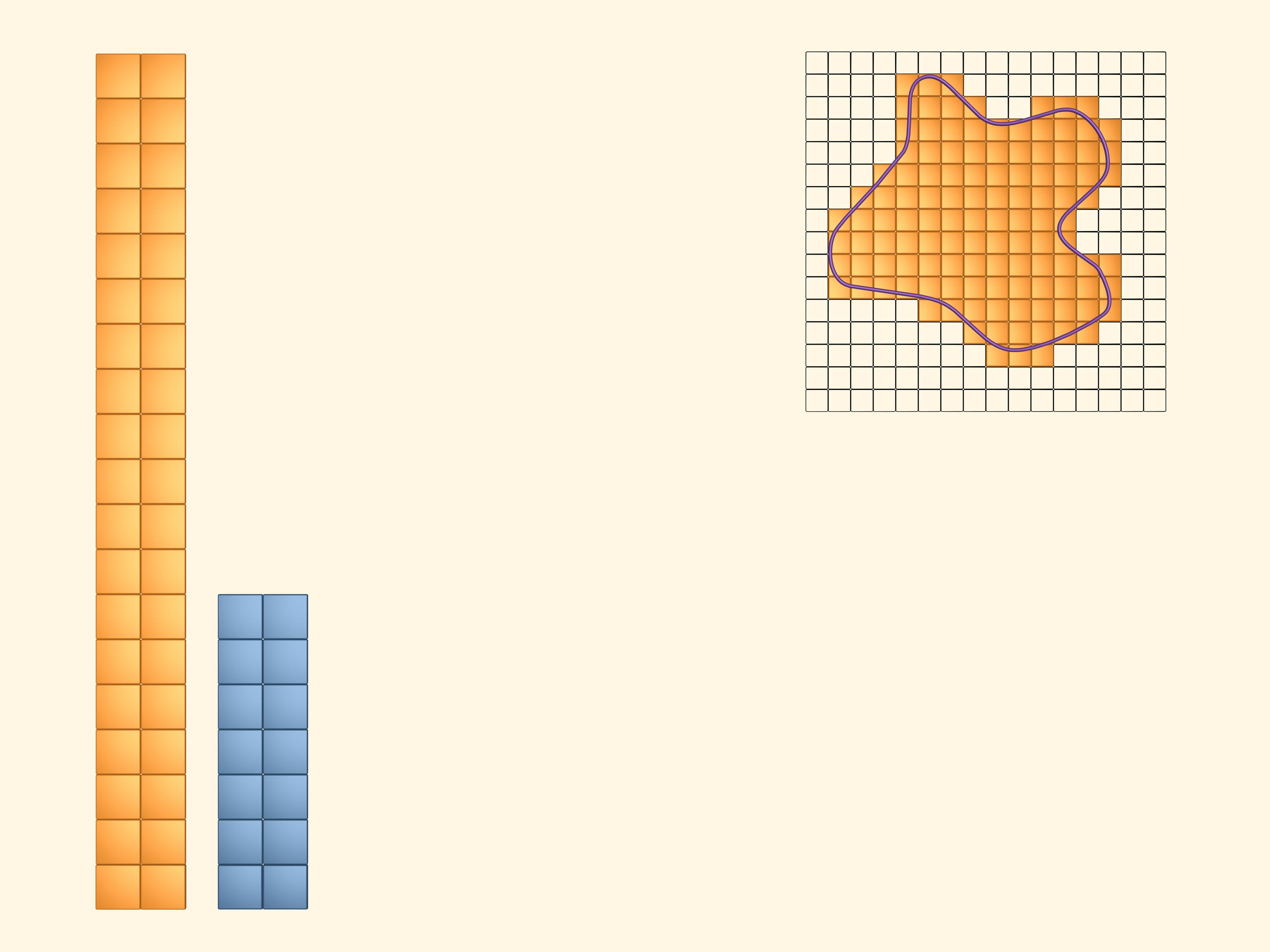
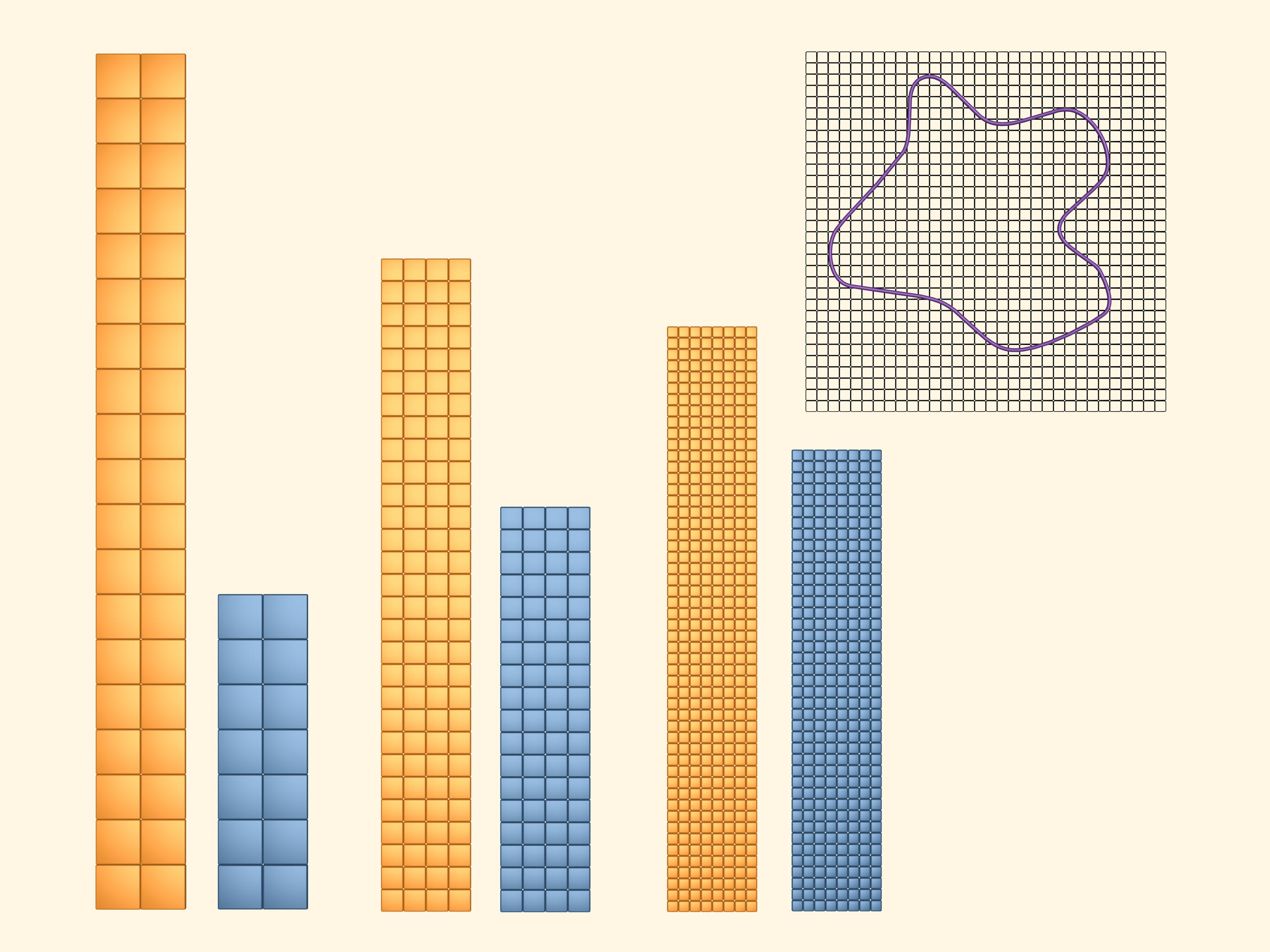
Наложим на изучаемую фигуру квадратную сетку.
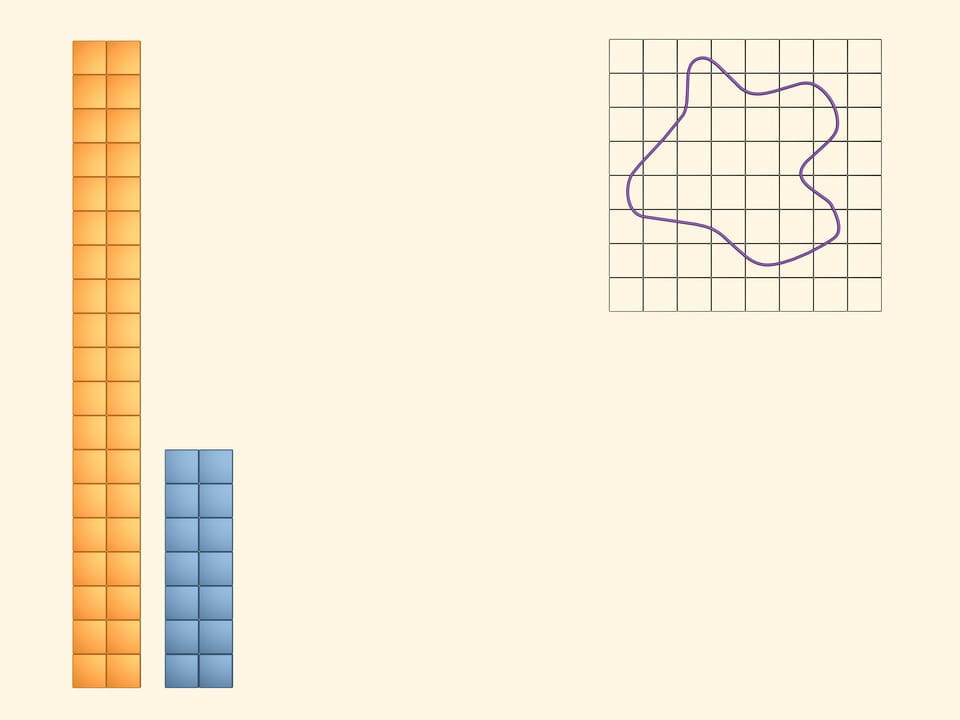
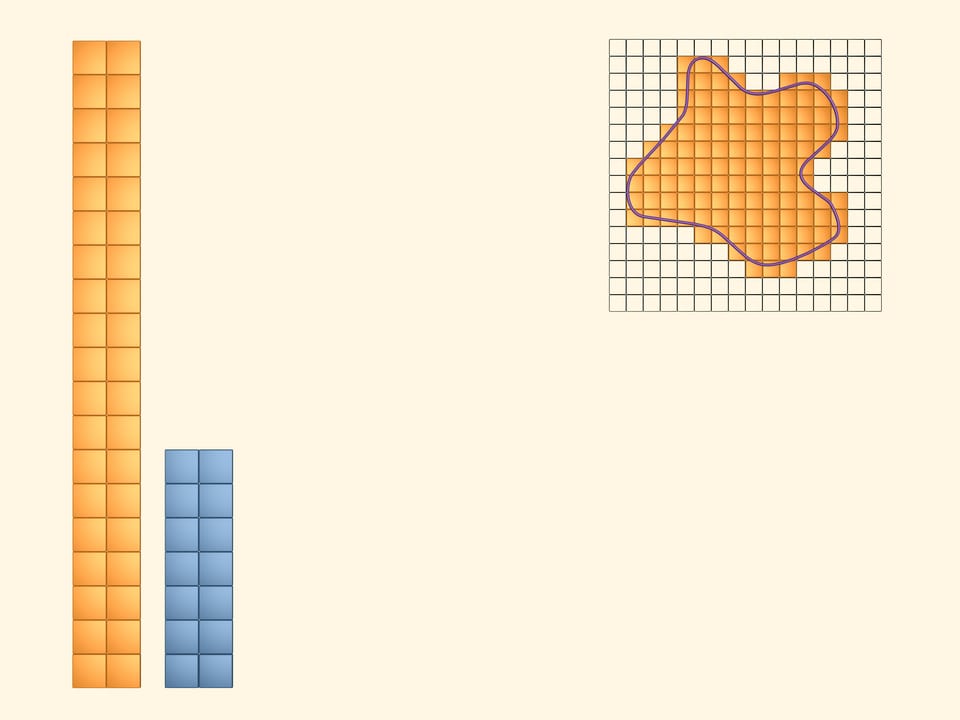
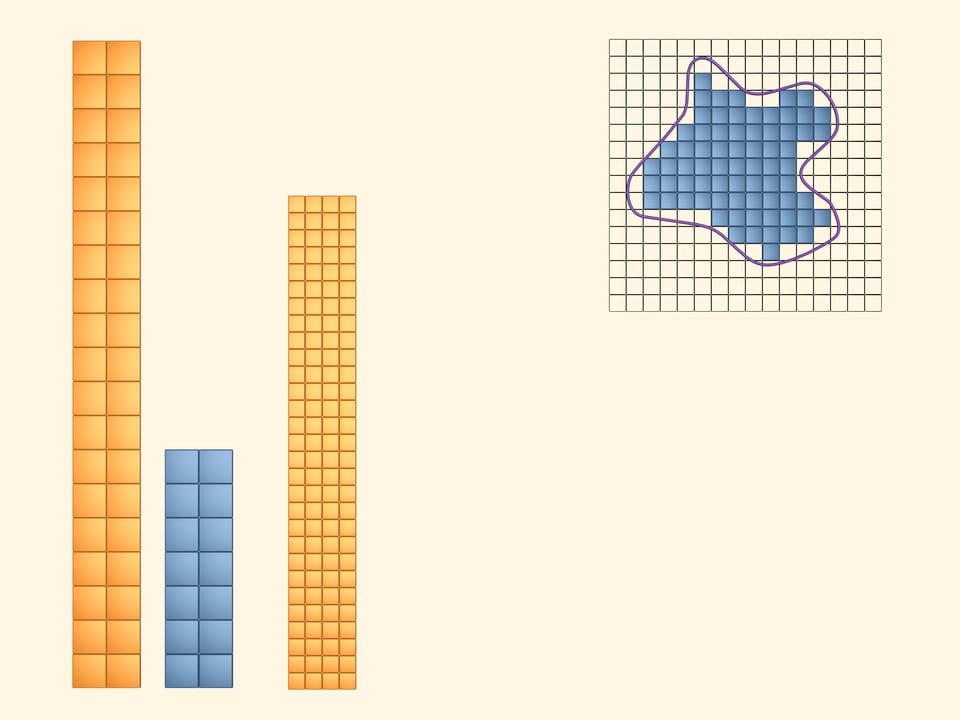
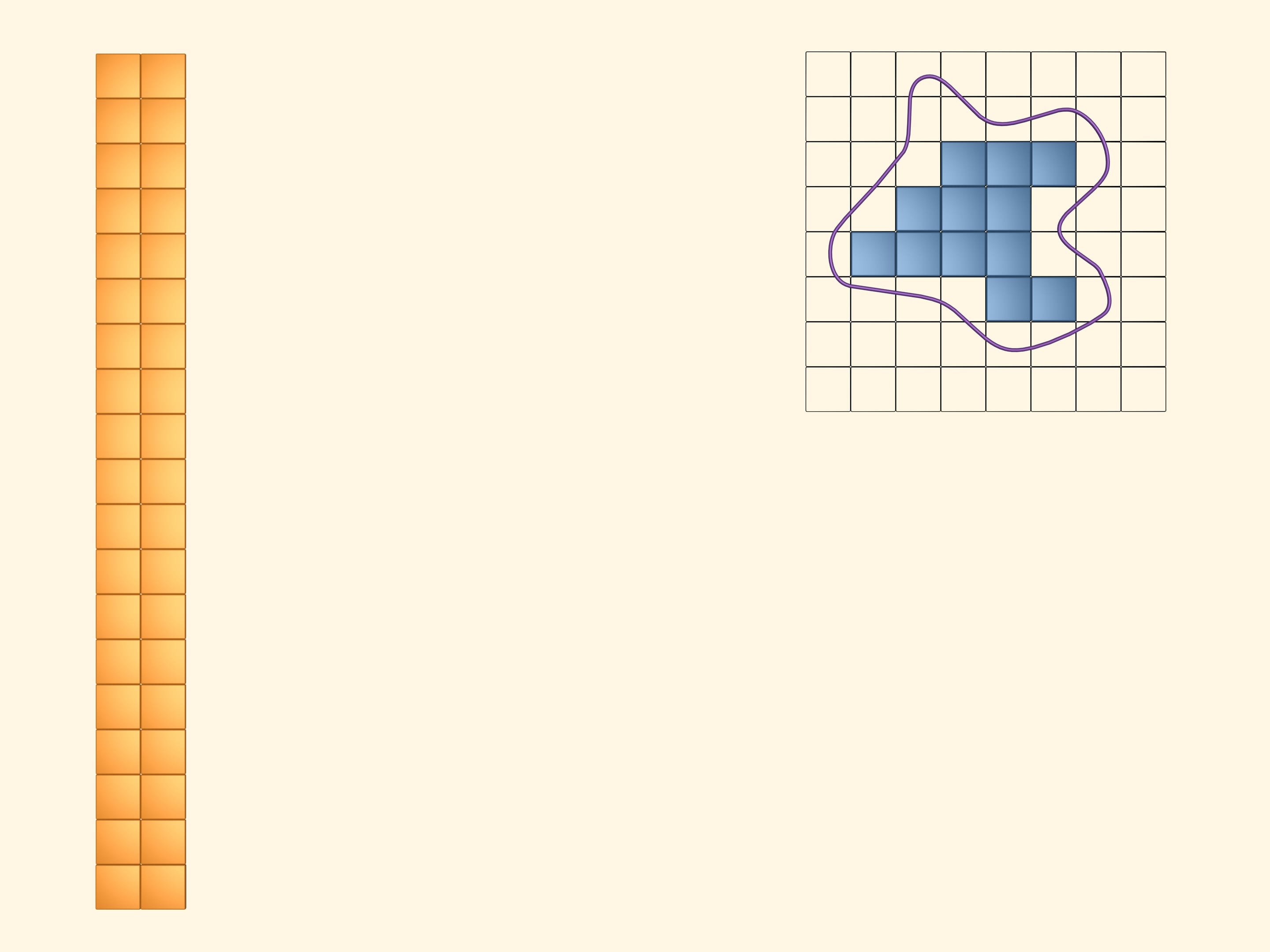
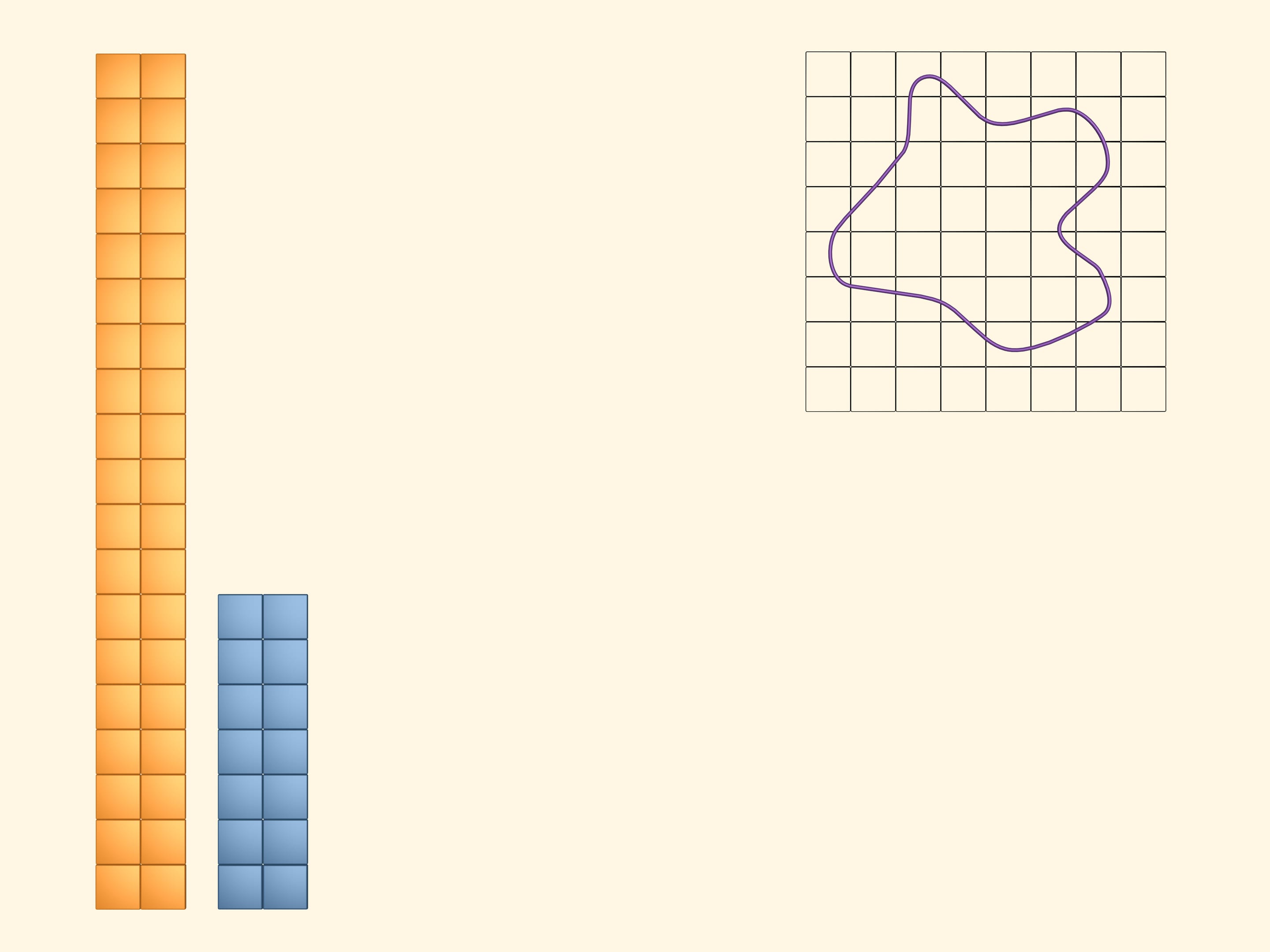
Покрасим в жёлтый цвет квадраты, которые хотя бы частично пересекаются с фигурой. Чтобы зрительно увидеть и подсчитать площадь, занимаемую жёлтыми квадратами, сложим из них прямоугольник. Очевидно, что величина, которую мы хотим назвать площадью изучаемой фигуры, меньше площади этого жёлтого прямоугольника.
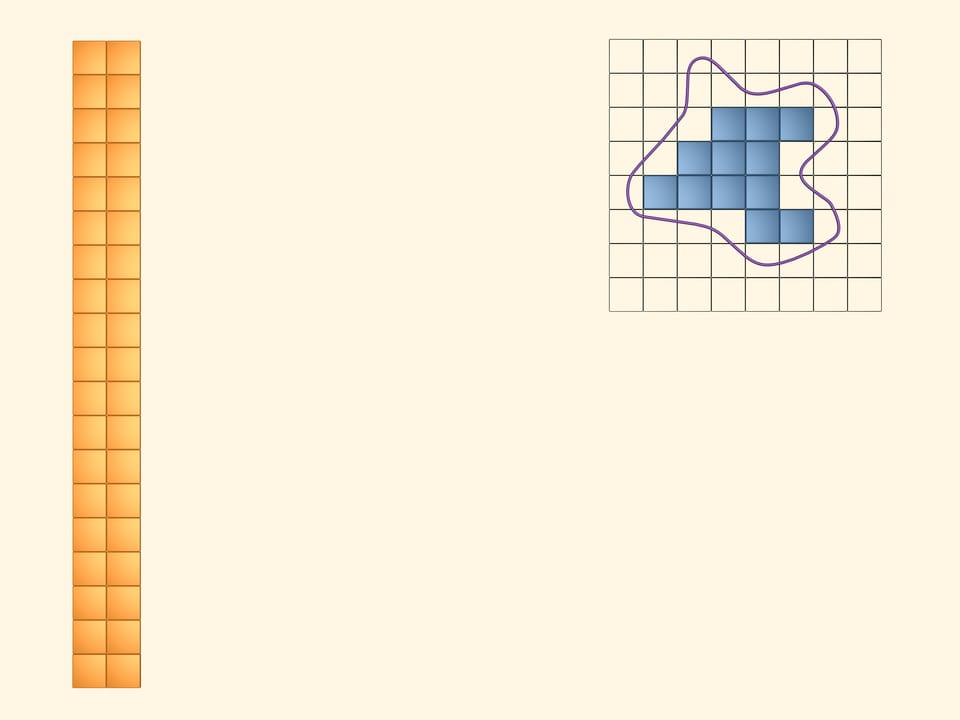
В синий цвет покрасим те квадраты, которые полностью лежат внутри нашей фигуры. Таких квадратов набралось, конечно, меньше, чем жёлтых. Выложим и из них прямоугольник. Площадь нашей фигуры больше площади этого синего прямоугольника.
Итак, то, что мы хотим назвать площадью изучаемой фигуры, больше площади синего прямоугольника и меньше площади жёлтого. Но площади этих двух прямоугольников сильно различаются, и пока мы плохо представляем, какова же искомая площадь.
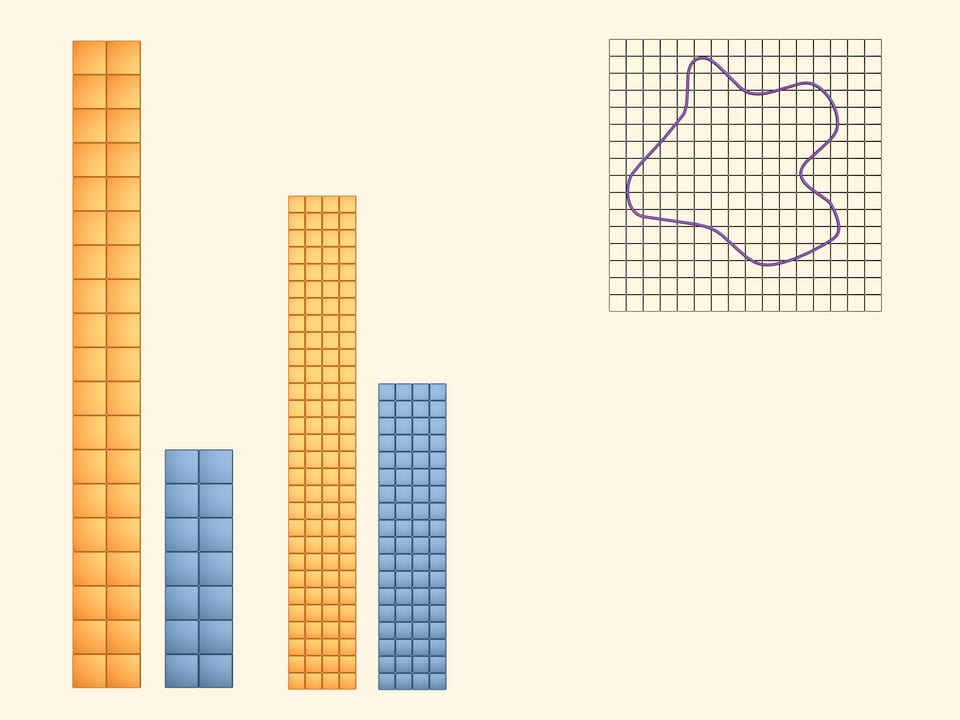
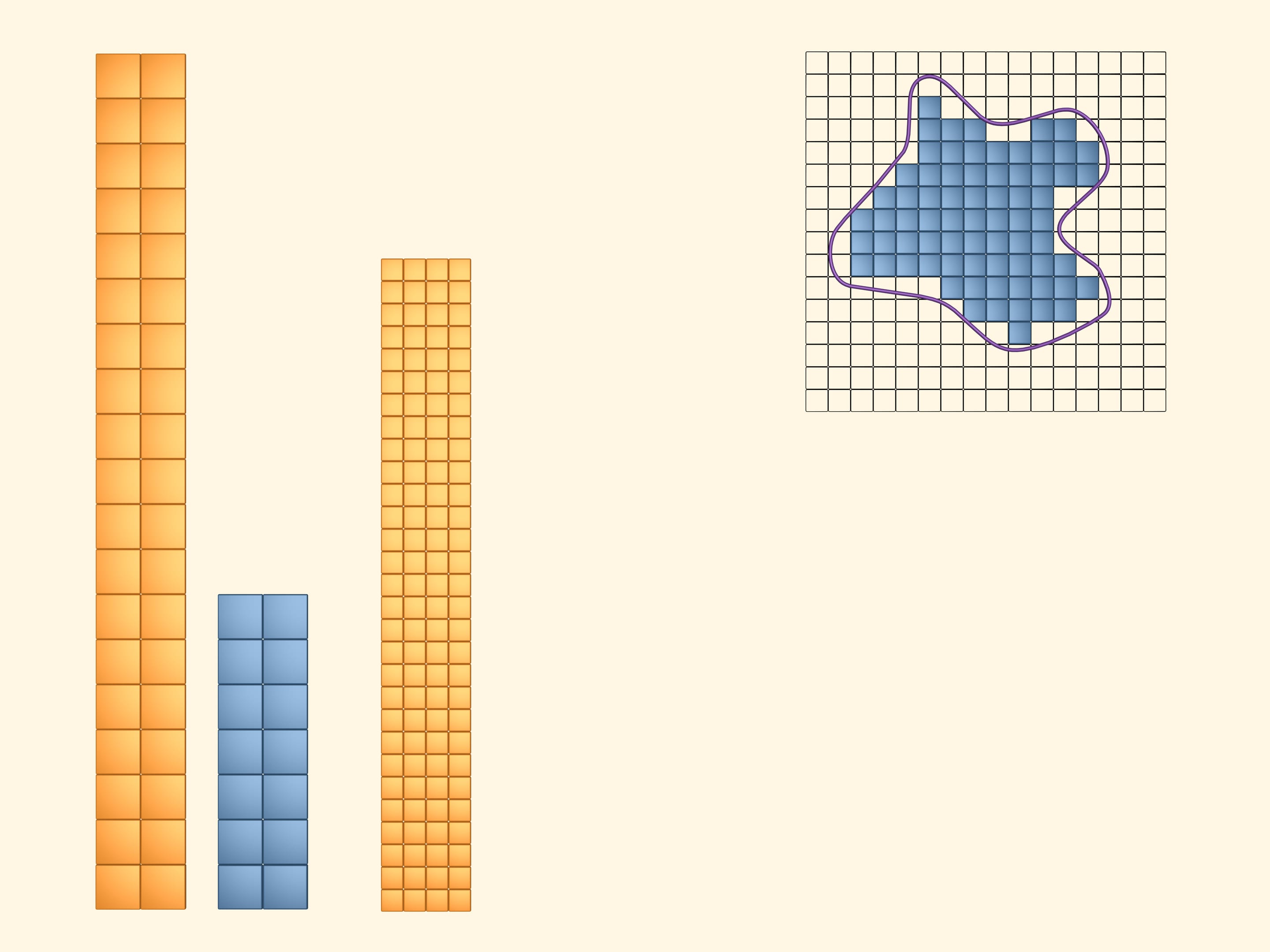
Для того чтобы получить более точные нижнюю и верхнюю границы искомой величины, рассмотрим сеточку из более маленьких квадратов. Повторим предыдущие действия. В жёлтый покрасим те квадраты, которые хотя бы частью пересекаются с фигурой. В синий — те, которые полностью лежат внутри фигуры. Снова площадь фигуры больше площади синего прямоугольника и меньше площади жёлтого. Но в этот раз, взяв более мелкую сетку, мы получили более точные границы.
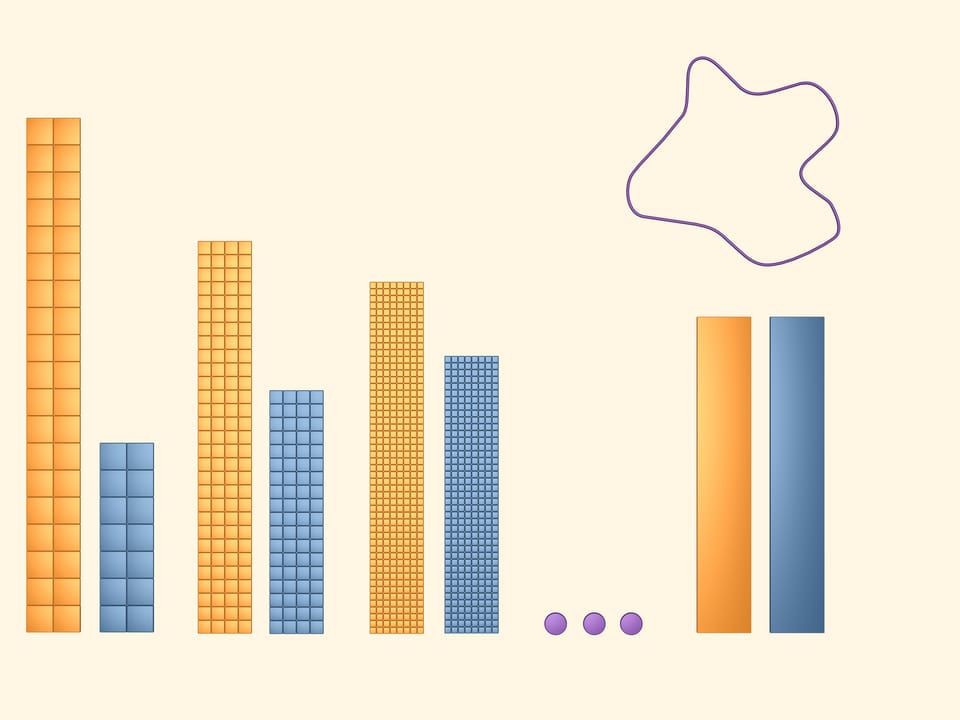
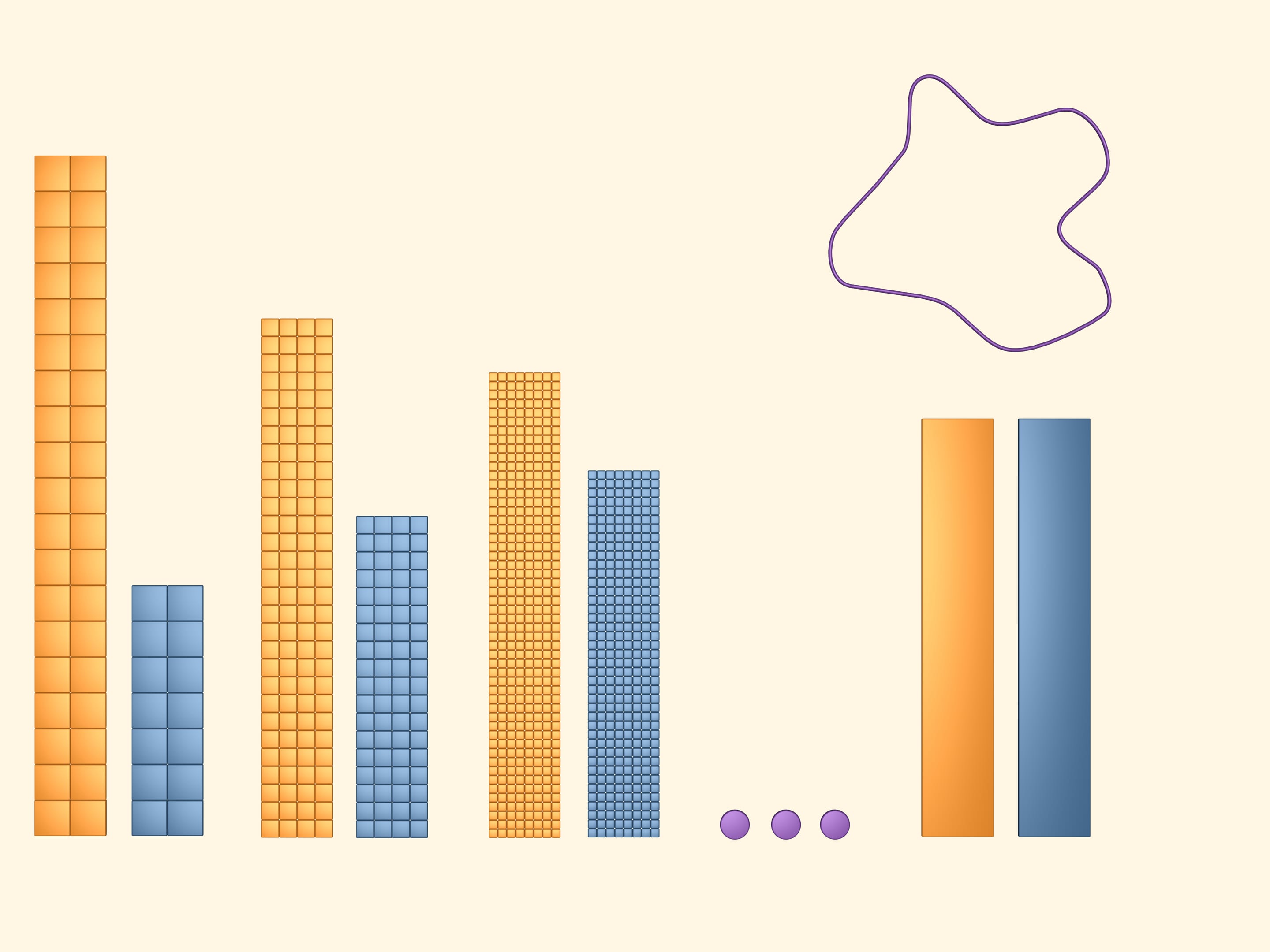
Рассматривая ещё более мелкую сетку, мы получим еще более точные верхнюю и нижнюю границы площади изучаемой фигуры.
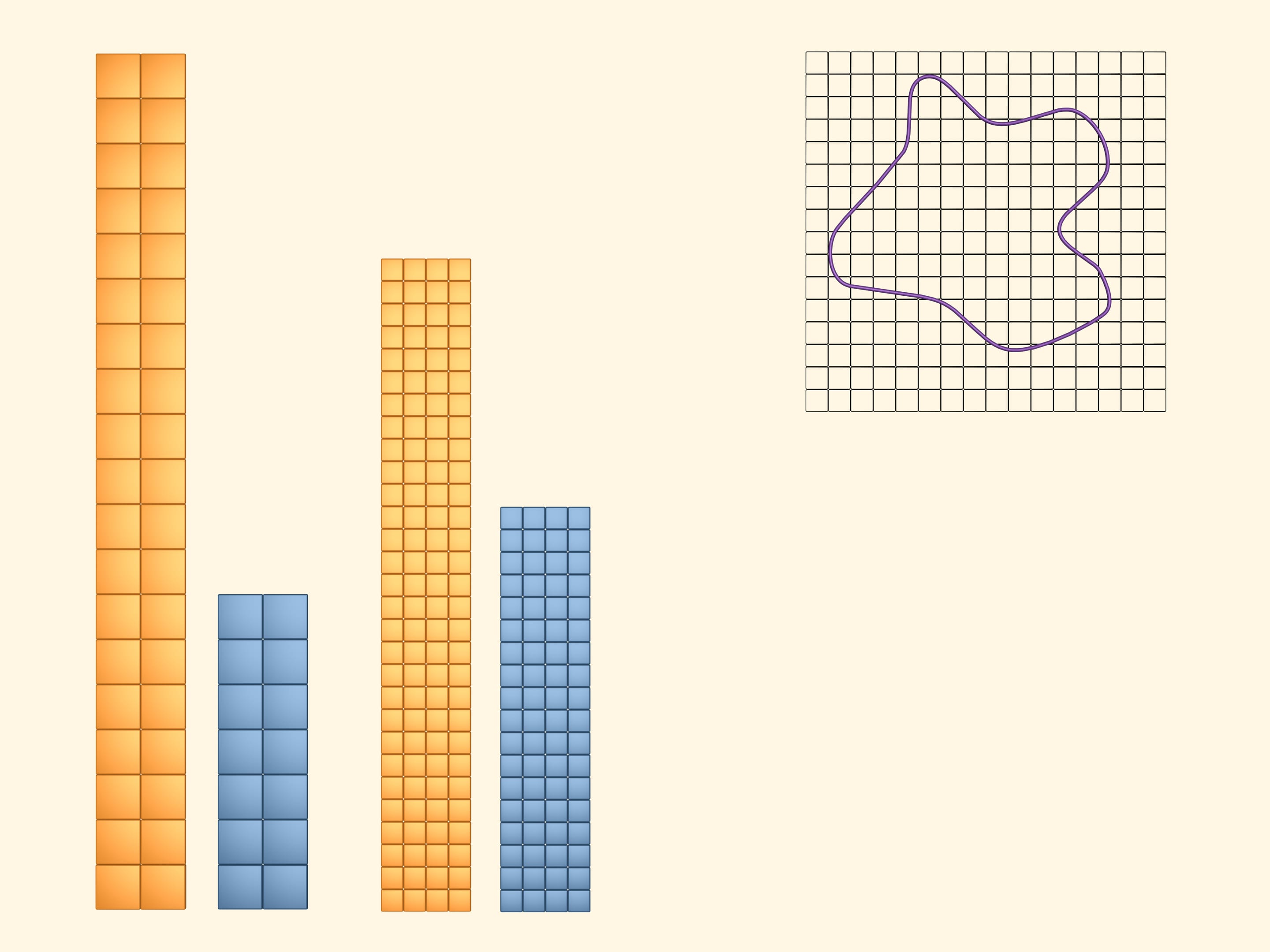
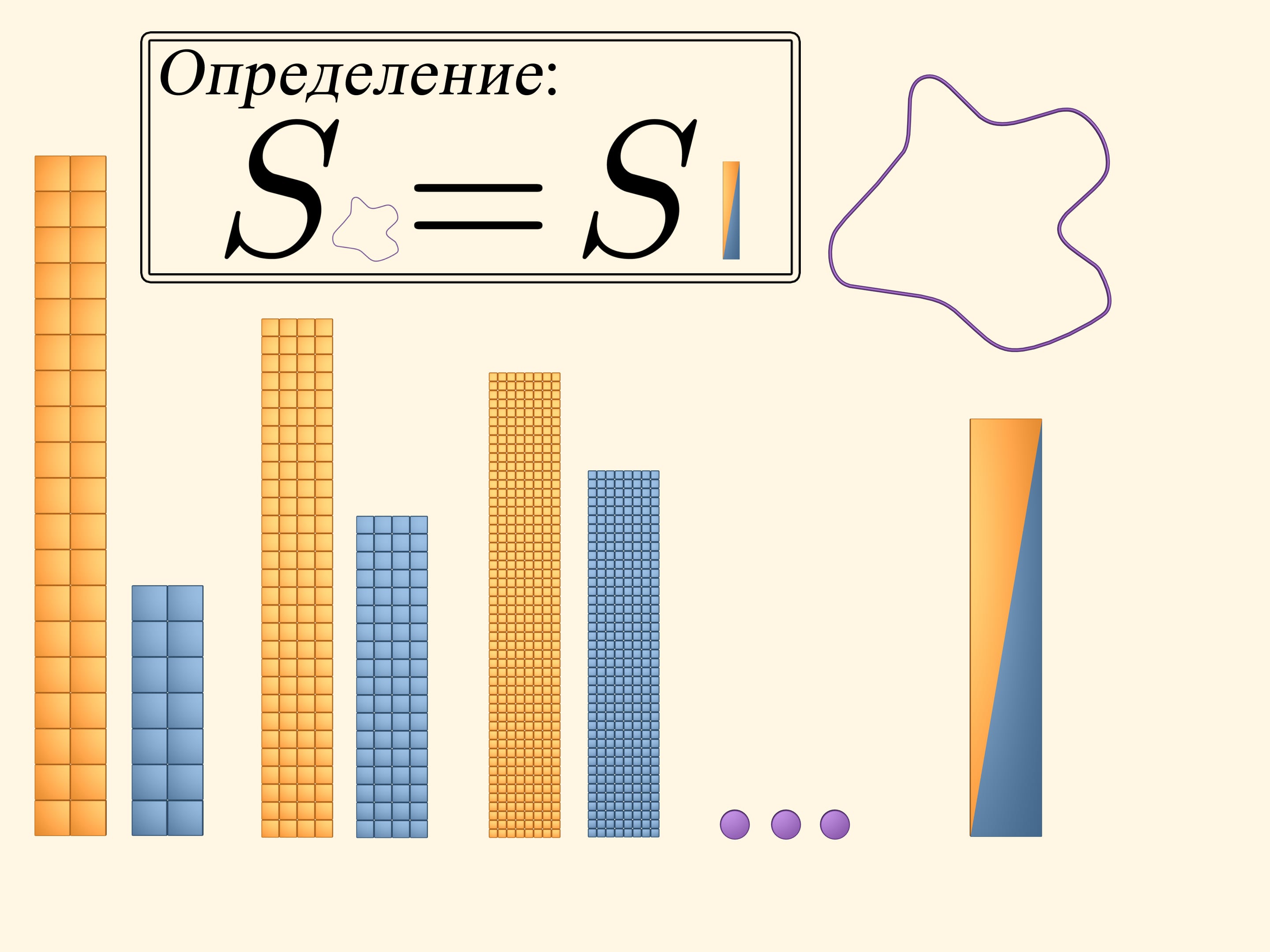
Будем продолжать уменьшать ячейки сетки, делая их всё мельче и мельче так, чтобы сторона квадратиков, из которых она составлена, стремилась к нулю. Абстрагировавшись от реальности, в математической модели считается, что делать квадратики можно сколь угодно маленького размера. Тогда, как говорят, в пределе, жёлтый и синий многоугольники окажутся равными. Рассмотрим прямоугольник, составленный из половинок синего и желтого прямоугольников (можно было рассмотреть и любой из них).
Площадью изучаемой фигуры по определению называется площадь двуцветного прямоугольника.
В жизни бывают случаи, когда необходимо приближённо определить площадь фигуры. При этом посчитанная площадь должна отличаться от настоящей не больше чем на некоторую заданную величину. Для решения этой задачи необходимо взять сетку из таких квадратиков, чтобы разница между площадями жёлтого и синего прямоугольников не превосходила удвоенной заданной величины погрешности. Тогда за площадь изучаемой фигуры нужно взять число, равное сумме площадей жёлтого и синего прямоугольников, поделённой пополам.