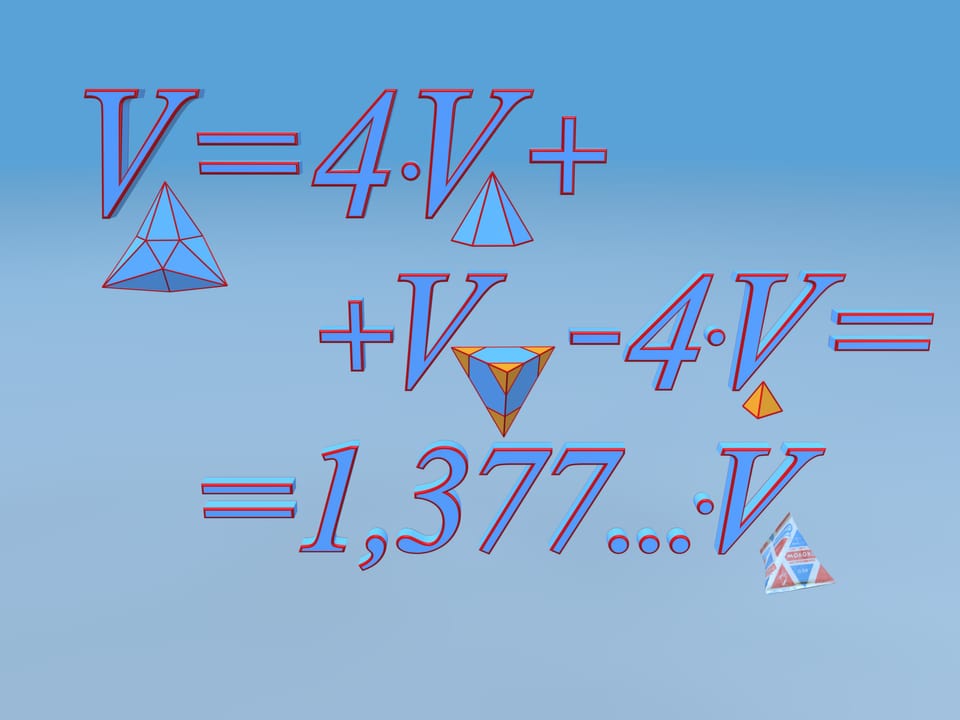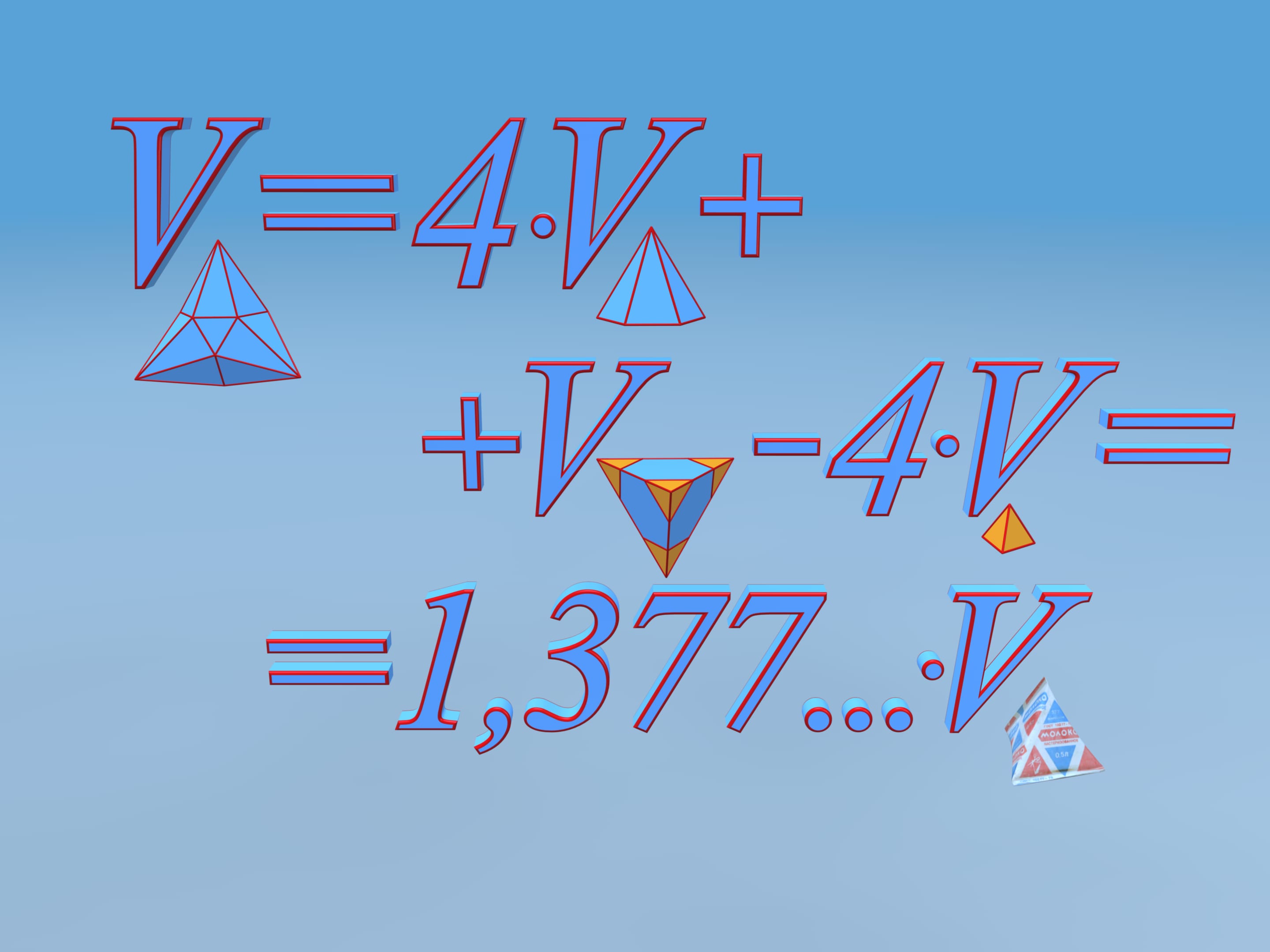Помните, как выглядел пакет молока в советское время? Удивительно, что вся страна покупала эти пакеты почти каждый день на протяжении более 20 лет, но мало кто сейчас помнит точно, что на них было нарисовано...
Но все конечно помнят, что пакет молока был в виде тетраэдра (правильной треугольной пирамиды). Изобрела пакеты в виде тетраэдра фирма Тетра Пак (Tetra Pak) в 40-х годах XX века, откуда и получила своё название. В те годы эта фирма сделала два важных нововведения. Во-первых, жидкие продукты начали наливать в картон. Во-вторых, изготовление тетраэдральных пакетов было настолько простым, что его можно было осуществлять прямо на молокозаводах.
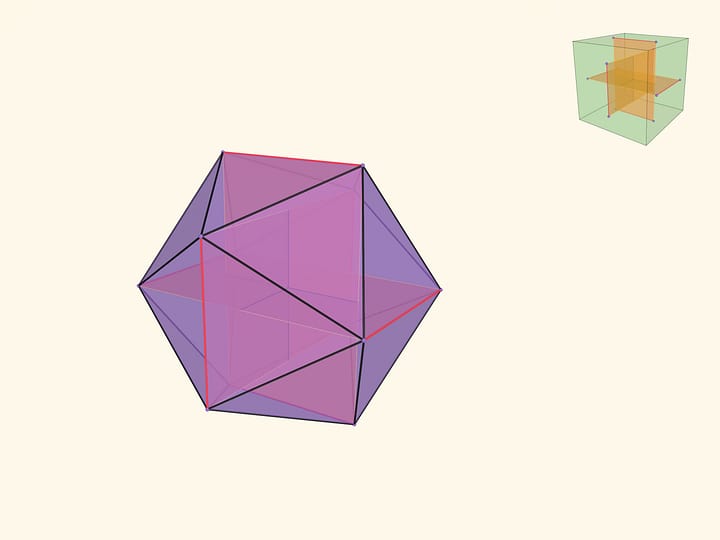
Вот так выглядел наиболее распространённый пакет молока в Советском Cоюзе: красные и синие треугольники; в форме тетраэдра (конечно, с небольшими искажениями).
Можно ли из куска картона, из которого сделан этот молочный пакет, сделать пакет с бóльшим объёмом, чем сам тетраэдр?
Математически задача формулируется так: можно ли из развёртки тетраэдра сделать многогранник с бóльшим объёмом?
А. Д. Александров 1912—1999
Александр Данилович Александров — российский математик, исследовавший обширный круг вопросов, включая геометрию выпуклых тел, теорию меры, теорию дифференциальных уравнений в частных производных и математические основания теории относительности.
По теореме А. Д. Александрова, выпуклый многогранник с той же развёрткой, но бóльшим объёмом сделать нельзя. Но, может быть, можно сделать невыпуклый с бóльшим объёмом?
Удивительно, но оказывается что можно!
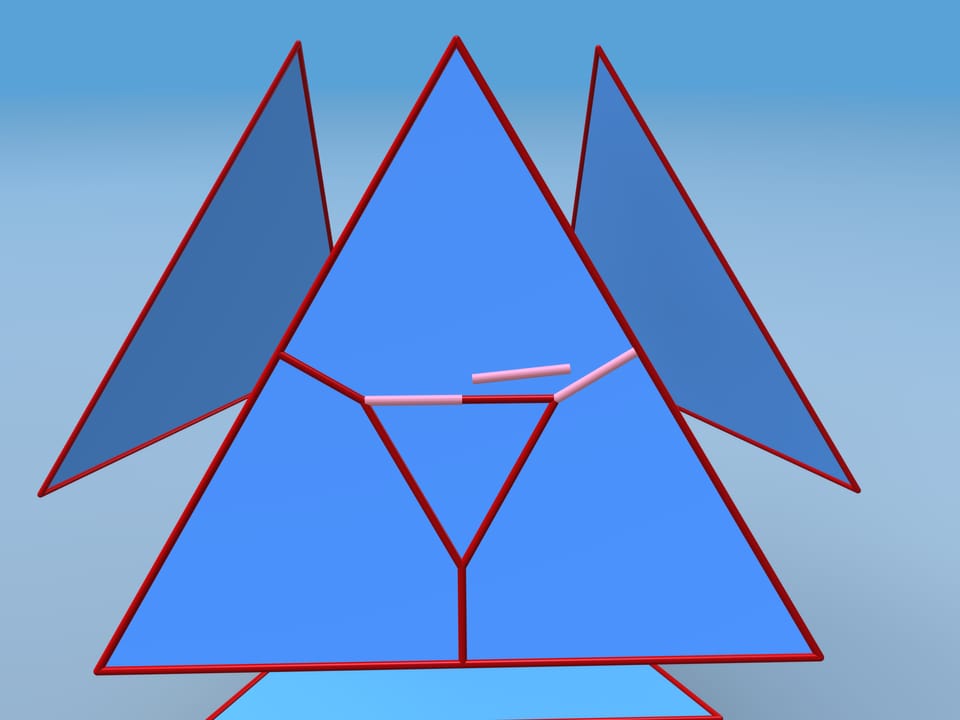
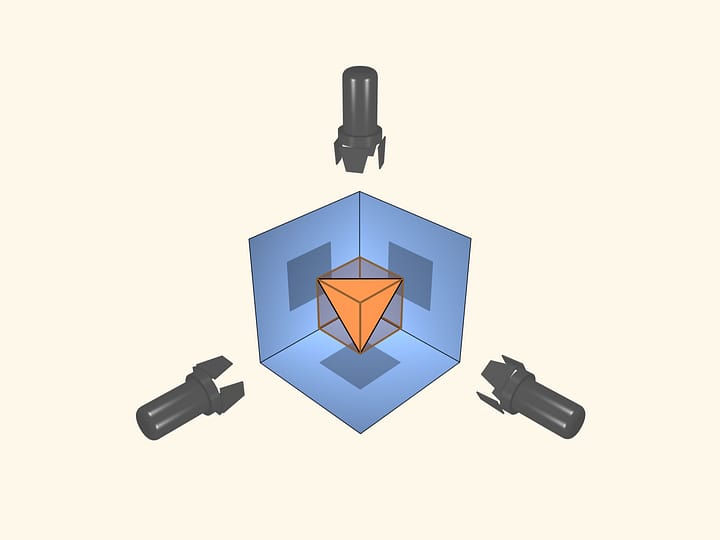
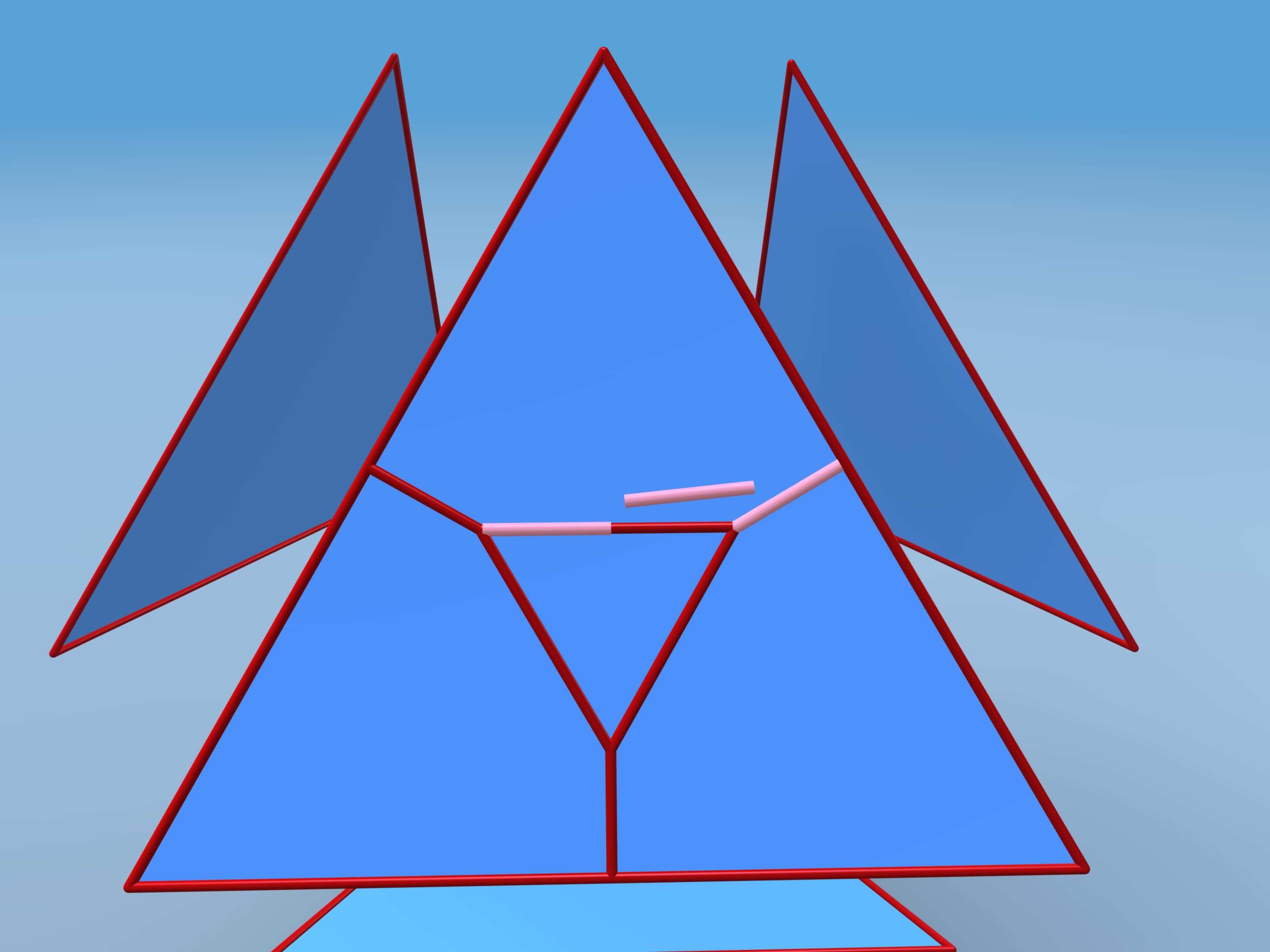
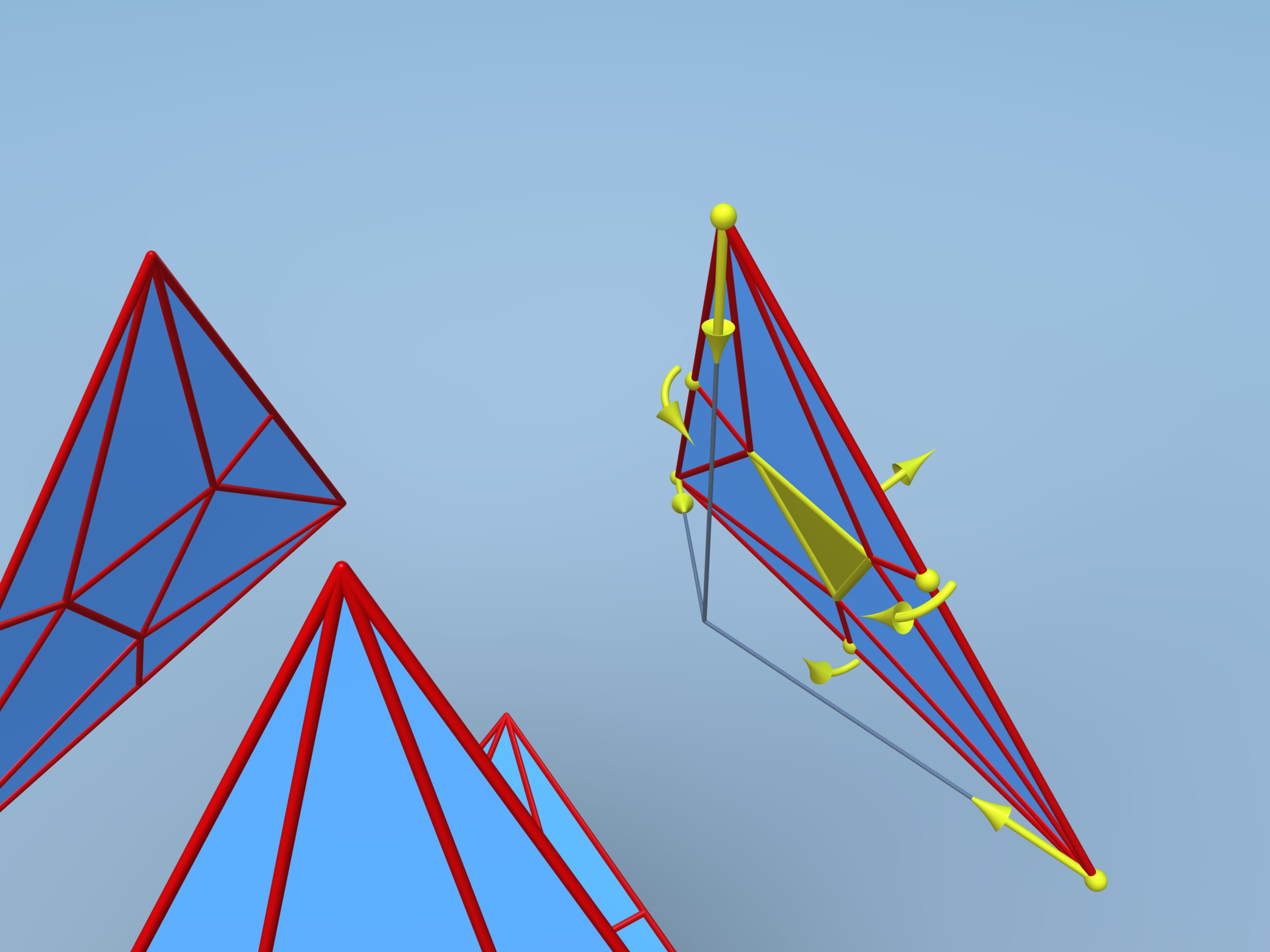
Давайте проследим за конструкцией, предложенной Дэвидом Бликером в 1996 году. Разведём грани и на каждой добавим дополнительные вершины и рёбра. Возьмём центральный правильный треугольник, определённый соотношением, что его сторона в два раза больше расстояния от его вершины до стороны грани. Проведём дополнительные рёбра.
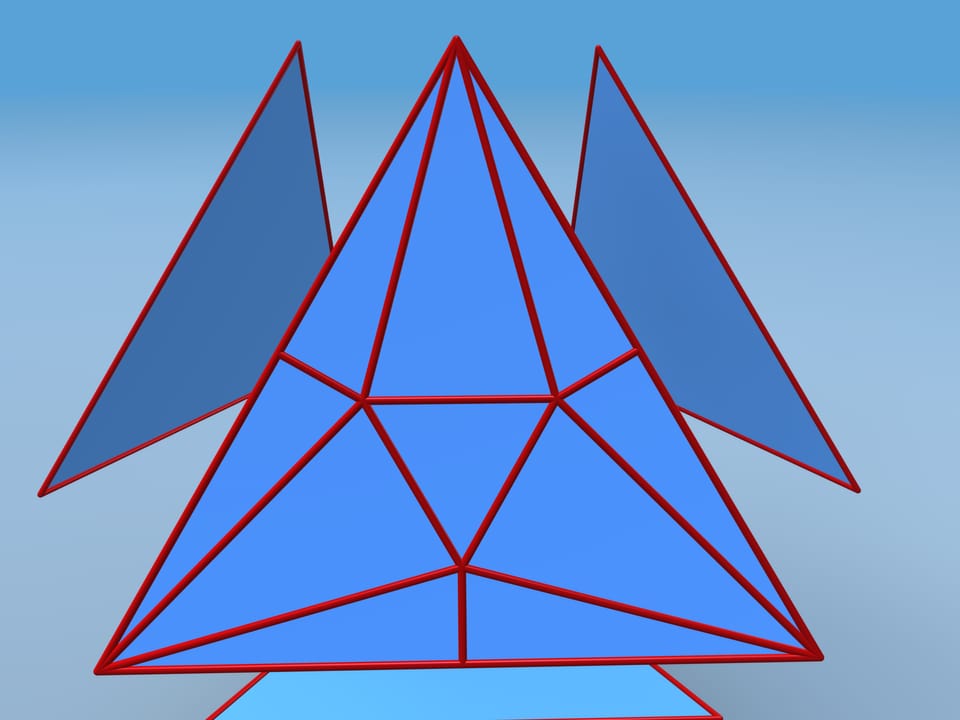
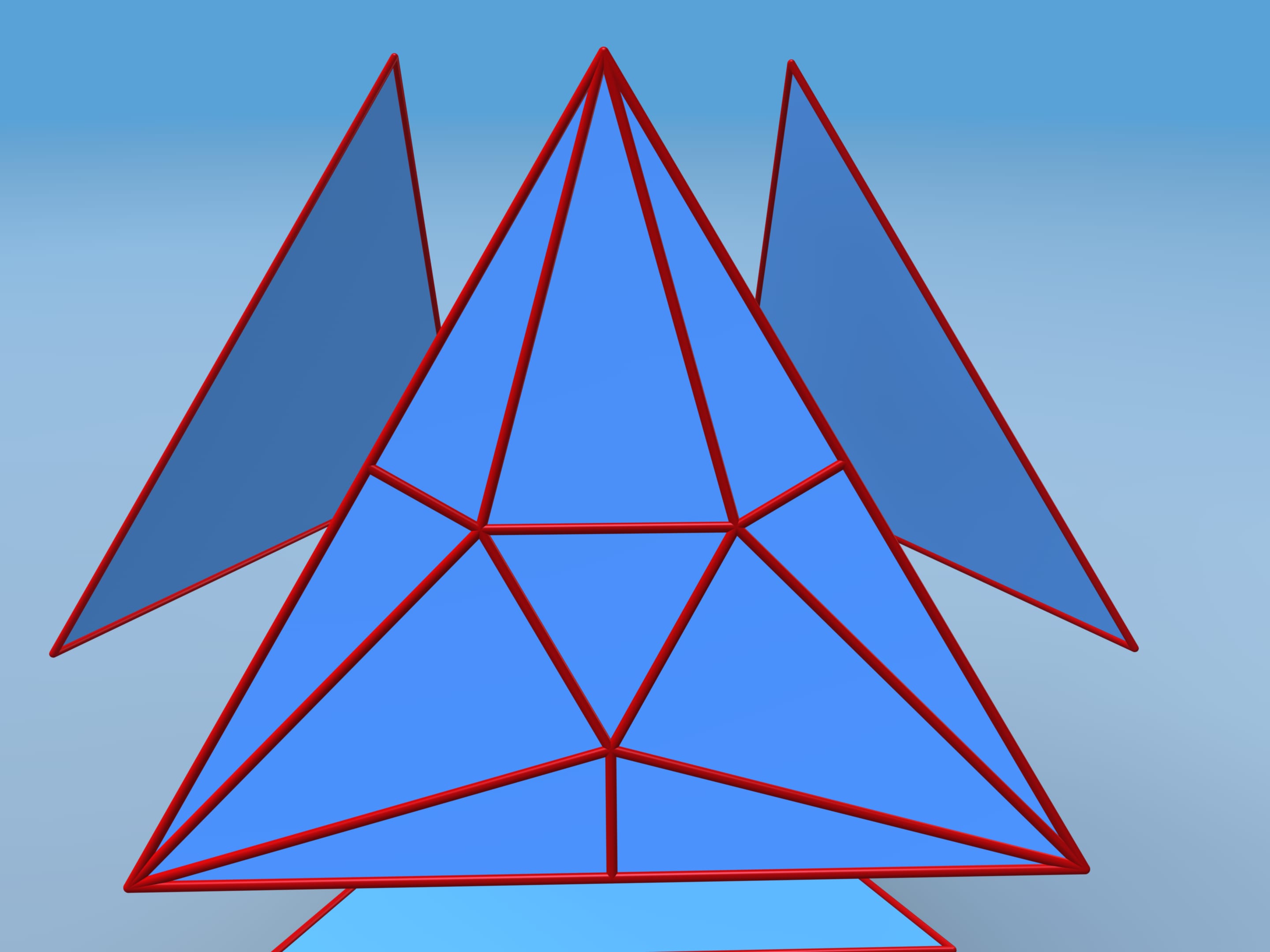
Те же построения сделаем на каждой грани. Изогнём каждую грань следующим образом: углы и середины сторон в сторону центра, а центральный треугольничек — от центра. Все грани изогнуты одинаково, и их можно склеить в многогранник. Некоторые новые грани лежат в одной плоскости, и рёбра между ними исчезают.
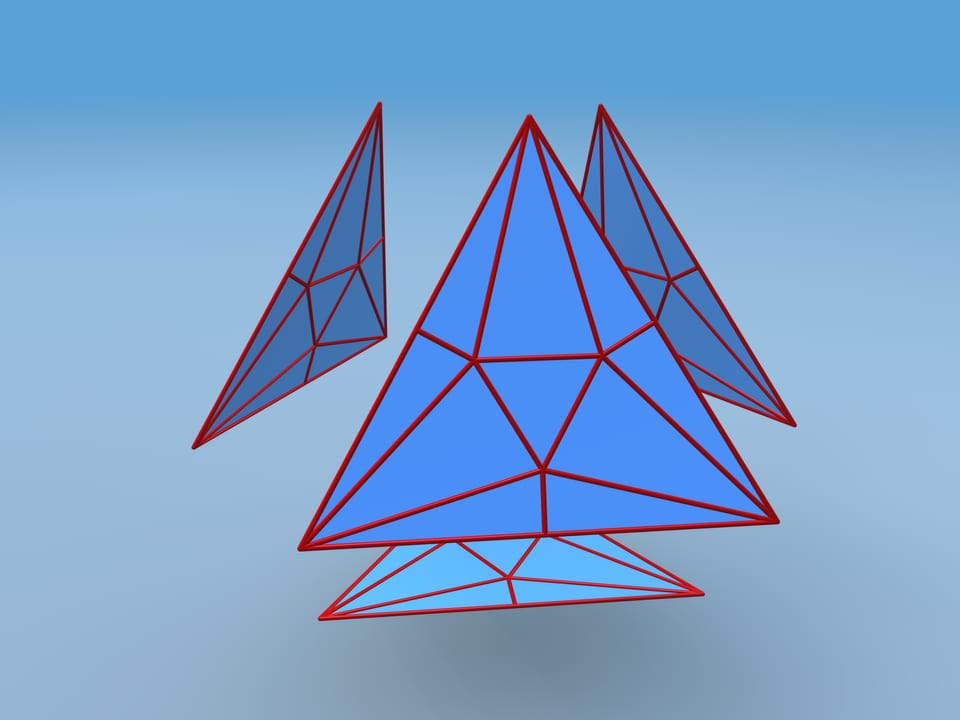
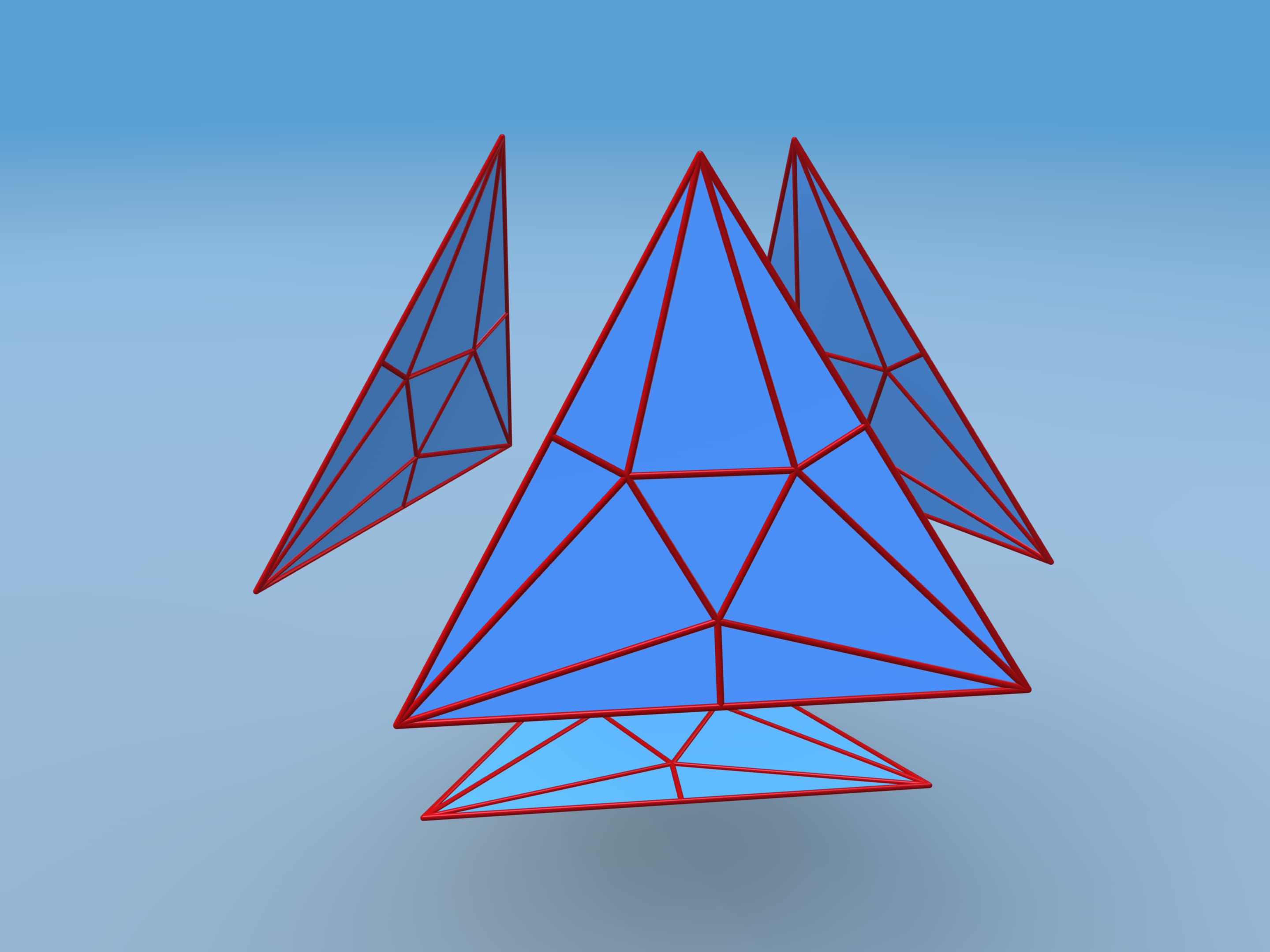
Подсчитаем объём получившегося многогранника. Для этого разобьём его на части. Полученный многогранник состоит из четырёх одинаковых шестиугольных пирамидок и фигуры, которая является усечённым тетраэдром. Чтобы проще посчитать объём, добавим усечённые у тетраэдра углы — маленькие тетраэдры, а от получившегося значения объёма отнимем объём добавленных кусочков.
Оказывается, что объём полученного таким способом многогранника больше чем на 37,7% превосходит объём изначального тетраэдра, имеющего ту же развёртку! Т. е. из куска картона, из которого делались тетрадральные пакеты, можно делать пакеты, которые вместительнее более чем на треть!
Удивительно, но тетраэдр не является исключением. Оказывается, что из развёртки любого выпуклого многогранника с треугольными гранями можно сделать невыпуклый многогранник с бóльшим объёмом. Эту теорему доказал в 1996 году Д. Бликер и привёл алгоритм, как это делать.
В своей статье, кроме многогранников с треугольными гранями, Д. Бликер рассмотрел два правильных многогранника, не попадающие в этот класс — куб и додекаэдр. Из их развёрток также можно сложить невыпуклые многогранники с бóльшим объёмом, чем у изначальных выпуклых. В 2005 году, когда создавался фильм, математики верили, что верна
Гипотеза
Из развёртки любого выпуклого многогранника всегда можно сложить невыпуклый многогранник с бóльшим объёмом.
Нерешённые задачи
Доказать (или опровергнуть) гипотезу.
Насколько большим может быть объём невыпуклого многогранника, сложенного из развёртки тетраэдра? Другого данного выпуклого многогранника?
Летом 2006 года, двумя математиками — аспирантом МГУ Гурием Самариным и Игорем Паком из MIT — независимо друг от друга было доказано, что гипотеза верна. Условие треугольности граней было лишь техническим моментом, позволившем Бликеру доказать свою теорему, но в задаче оно не по существу — теорема верна и без этого условия.
Литература
Bleecker, David D. Volume increasing isometric deformations of convex polyhedra // Journal Differential Geometry. — 1996. — V. 43. — P. 505—526.