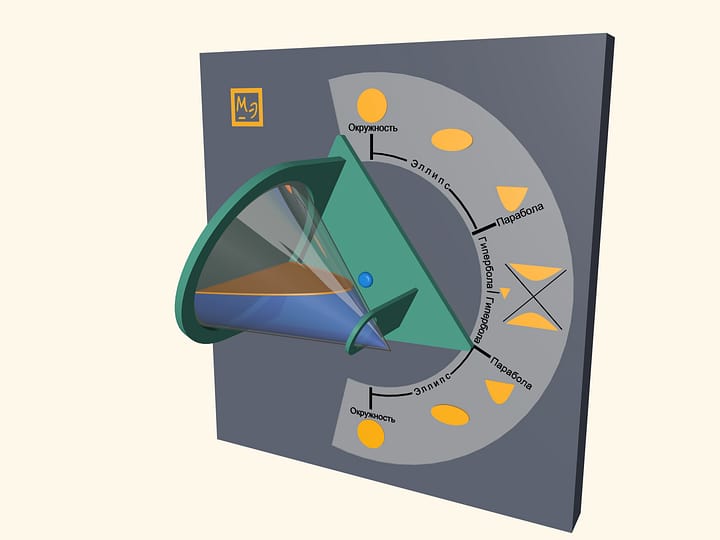
Любую гладкую кривую можно увидеть, нарисовав не саму кривую, а множество касательных к ней. Понятие огибающей подробно описано в сюжете Парабола: изонить, в котором в качестве огибающей семейства прямых возникает парабола. Но построение касательных не такое простое дело. Продемонстрируем, как увидеть конические сечения — эллипс, гиперболу, параболу — ничего не считая и не рисуя, а просто складывая листок бумаги.
--:--
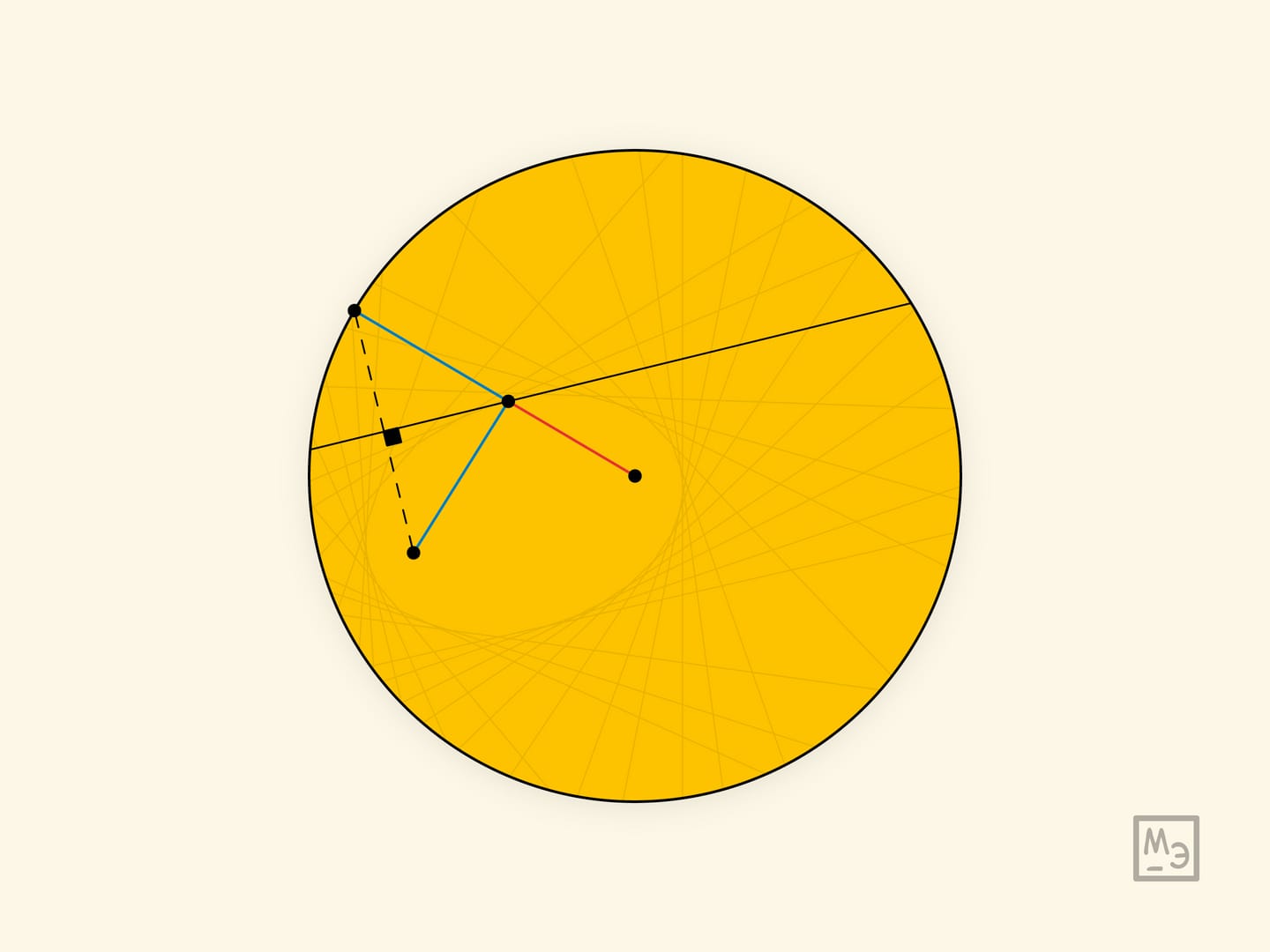
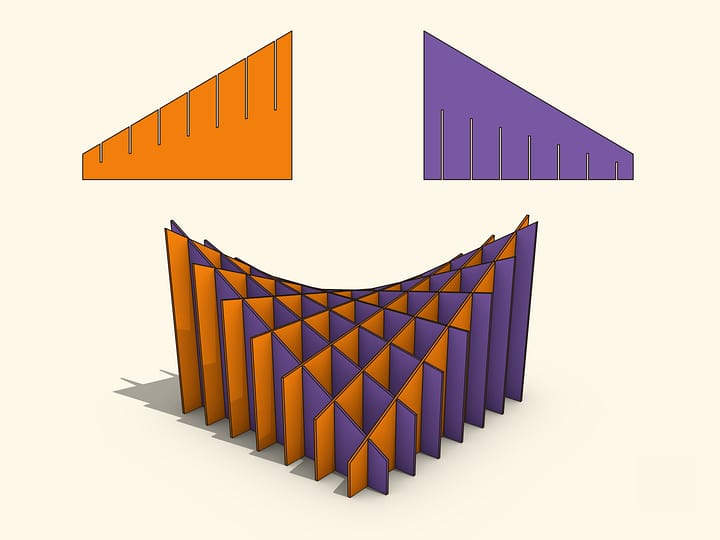
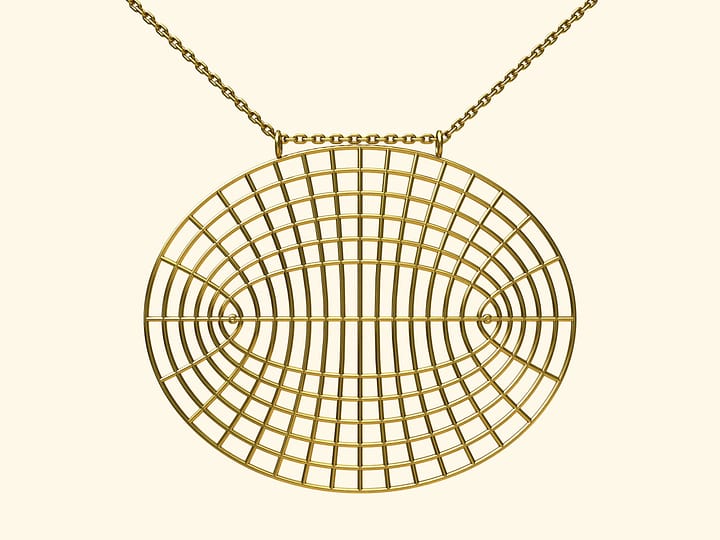
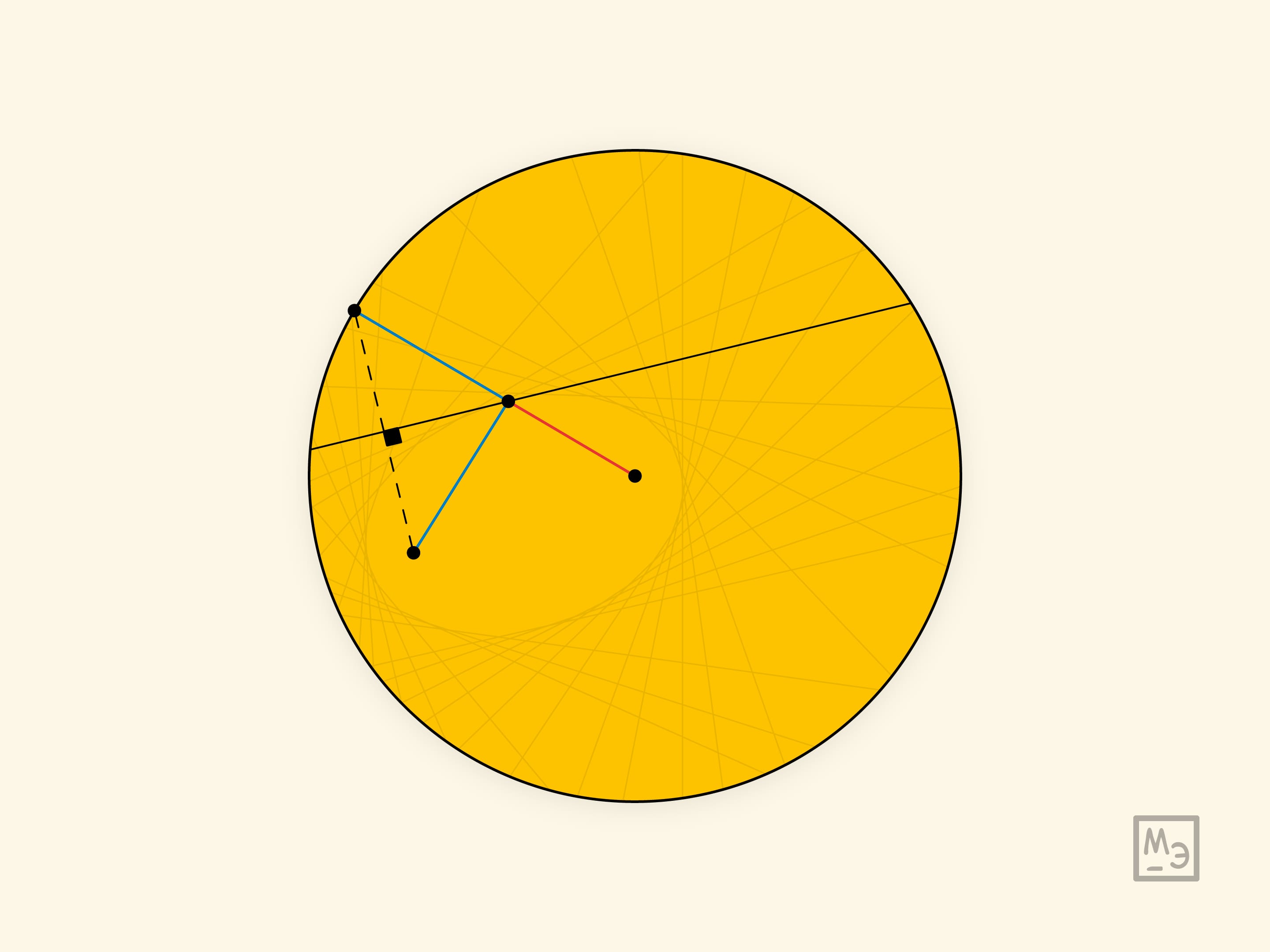
Вырежем из бумаги круг и отметим на нём точку. Перегнём круг так, чтобы граница загибаемого участка прошла через отмеченную точку, и разгладим сложенный листочек в сторону сгиба. Развернём круг, на нём осталась линия (отрезок) сгиба. Сложим круг по другому направлению, опять же, чтобы граница прошла через отмеченную точку. После нескольких таких операций станет видимым эллипс, как огибающая линий сгиба. Отмеченная точка круга является одним из фокусов полученного эллипса, а вторым фокусом является центр бумажного круга.
Огибающая линий сгиба действительно является эллипсом. Складывание листа бумаги является построением серединного перпендикуляра к отрезку, соединяющему две совмещаемые точки. Следовательно, отрезок от точки касания линии сгиба с эллипсом до отмеченной точки-фокуса равен отрезку до точки окружности, которая совмещалась с фокусом при данном сгибе. Вместе с отрезком, проведённым из центра окружности в точку касания, они составляют радиус. Таким образом, сумма расстояний до фокусов из определения эллипса равна радиусу бумажного круга.
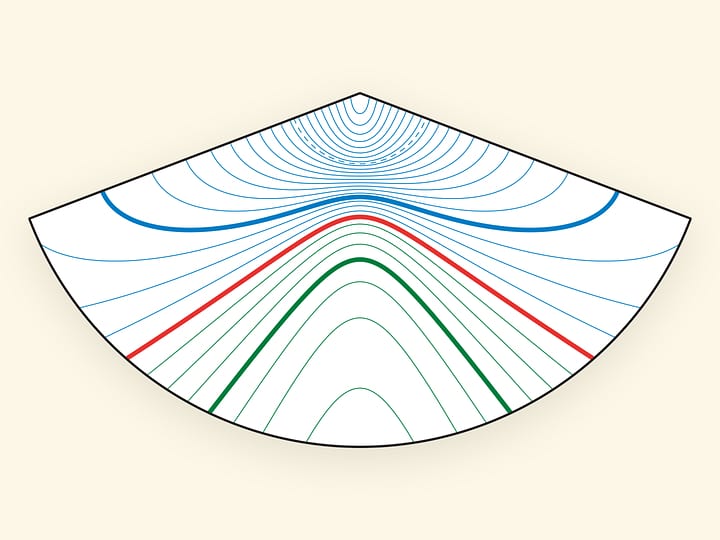
Аналогичным способом можно «нарисовать» гиперболу. Только отмеченная точка должна лежать вне круга, и тут проще всего приклеить бумажный круг скотчем к обычному писчему листу бумаги. Складывая круг, следует соблюдать то же условие: граница круга должна проходить через отмеченную точку. Линии (отрезки) сгиба являются касательными к одной из ветвей гиперболы. Отмеченная точка — один из фокусов гиперболы, а второй фокус — центр бумажного круга. В данном опыте уже разность расстояний от точки гиперболы до фокусов равна радиусу бумажного круга.
--:--
Можно рисовать касательные к гиперболе и на прямоугольном листе-основании, пользуясь согнутым кругом как линейкой для проведения отрезка.
--:--
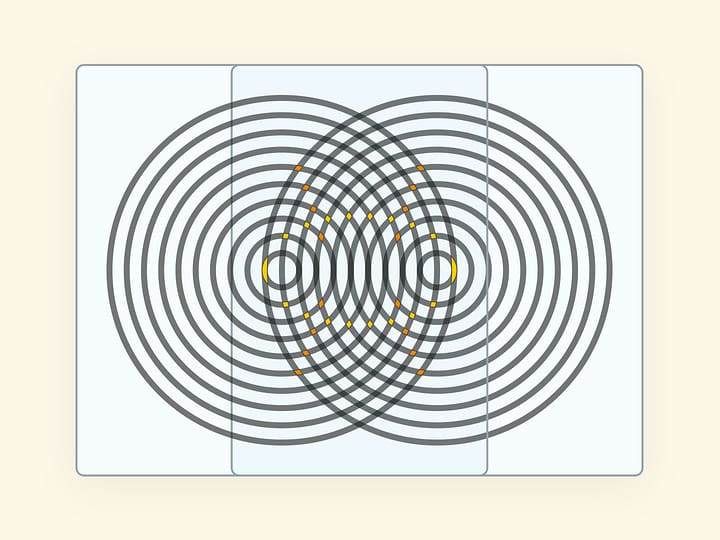
А вот для «рисования» параболы не нужен даже бумажный круг. Возьмём обычный прямоугольный лист бумаги и недалеко от его стороны отметим точку. Будем складывать лист по различным направлениям так, чтобы эта сторона всегда проходила через отмеченную точку. Огибающая сгибов — парабола.
--:--
Фокусом параболы является отмеченная точка, а директрисой — использованный край листа бумаги. Само складывание реализует геометрическое определение параболы: расстояния от точки до фокуса и до директрисы равны.
Похожие картинки можно увидеть в миниатюрах Эллипс как огибающая, Гипербола как огибающая, Парабола как огибающая. Но в них надо уметь строить перпендикуляр к отрезку, а в указанных методах складывания листочка эта операция «зашита» в сам способ складывания.
Читатель может задать резонный вопрос: почему для эллипса и гиперболы требуется окружность (круг), а для параболы — нет. На самом деле в случае параболы окружность тоже присутствует, только бесконечно большого радиуса — в виде края листа бумаги. Родственный факт: у эллипса и гиперболы по два фокуса, а у параболы — один.
Литература
Другие модели раздела «Конические сечения»
