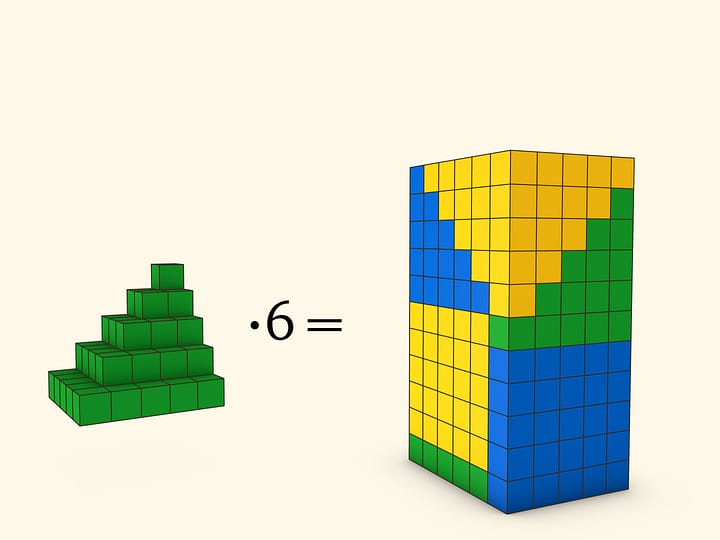Цветные кубики могут быть полезны не только в младших классах, но и в средней школе. С их помощью можно геометрически демонстрировать различные числовые соотношения.
Классическим примером является визуализация подсчёта Гауссом суммы первых чисел натурального ряда. Таким же способом можно продемонстрировать и сумму любой арифметической прогрессии.
Сумму нечётных чисел можно посчитать через площадь квадрата как минимум двумя способами: закладывая его разноцветными уголками или четырьмя одинаковыми по площади фигурами.
Для подсчёта суммы квадратов первых чисел придётся выйти в пространство, и проще сделать отдельную модель, а с помощью числовых кубиков можно выработать гипотезу, чему равна сумма кубов первых чисел.
Ну а с начинающими знакомиться с математикой на числовых кубиках можно разобрать, что такое квадрат и куб числа, проиллюстрировать, чему равен квадрат суммы двух чисел.
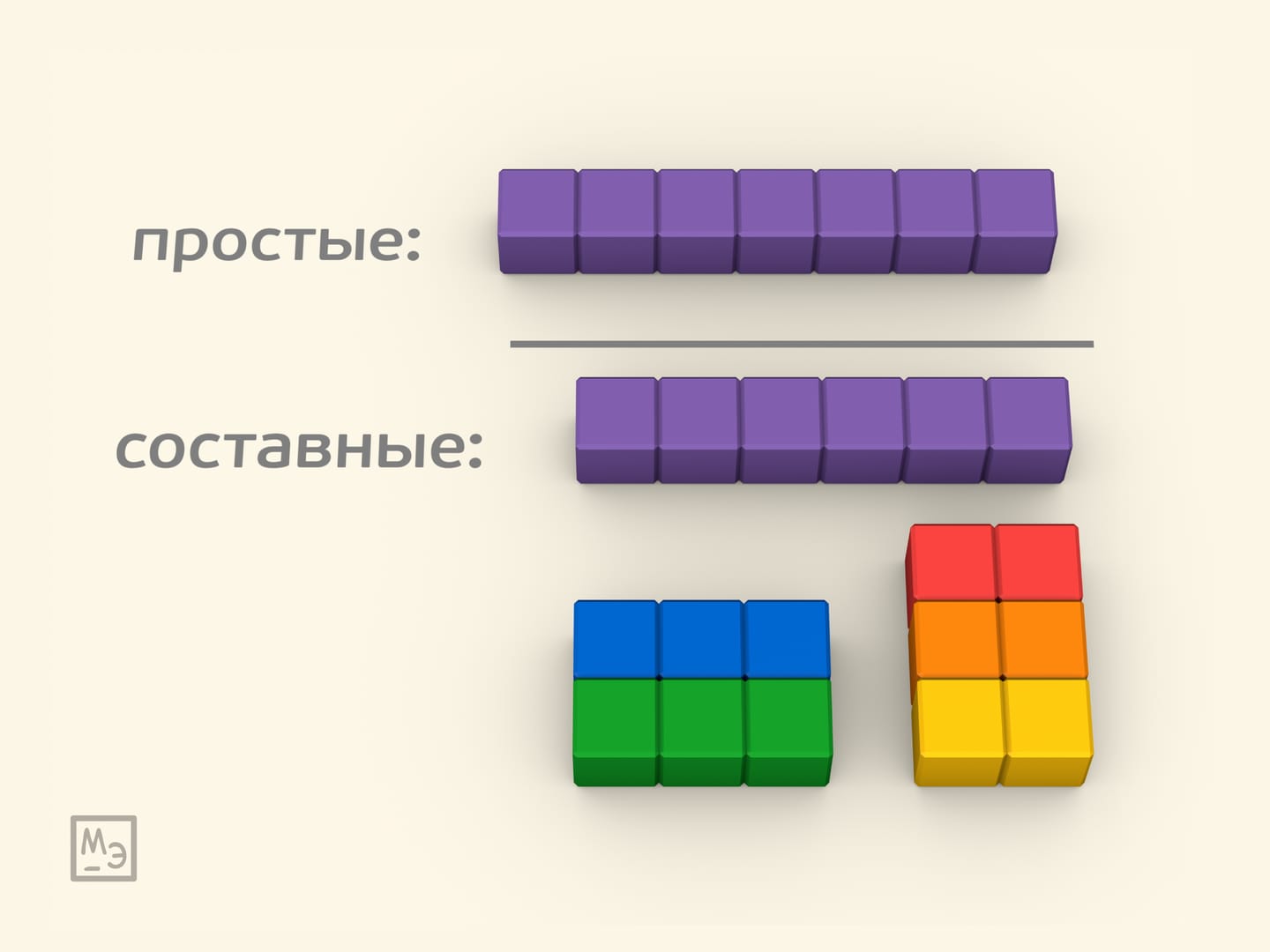
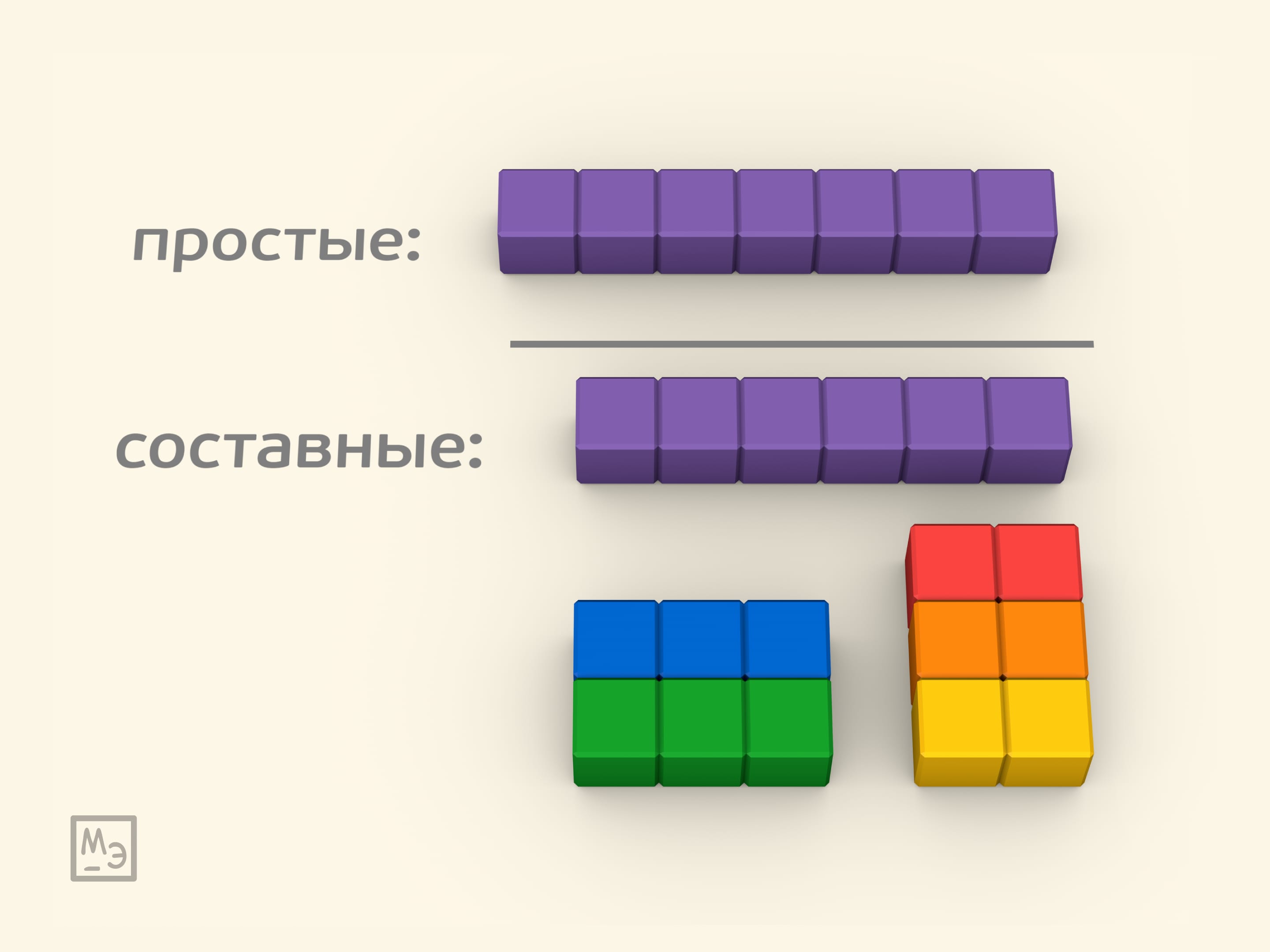
Используя кубики, можно дать наглядную интерпретацию понятиям простого числа и составного числа. Например, из шести кубиков можно сложить прямоугольник и в один ряд $1\times 6$, и прямоугольники $2\times 3$ или $3\times 2$. А вот пять или семь кубиков в прямоугольник можно сложить только одним способом — в один ряд.
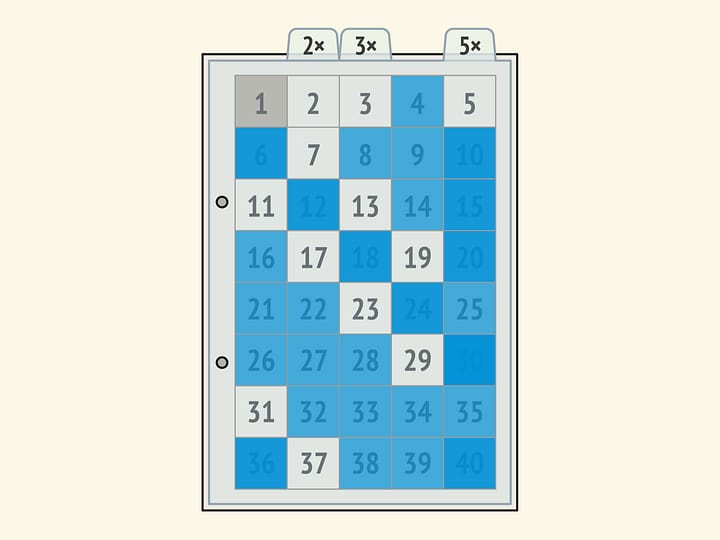
Игра с детьми в складывание из кубиков прямоугольников со сторонами $m$ и $n$, а затем подсчёт количества кубиков в получившемся прямоугольнике, позволит подготовить их к изучению таблицы умножения.
Другие модели раздела «Числа и их свойства»
