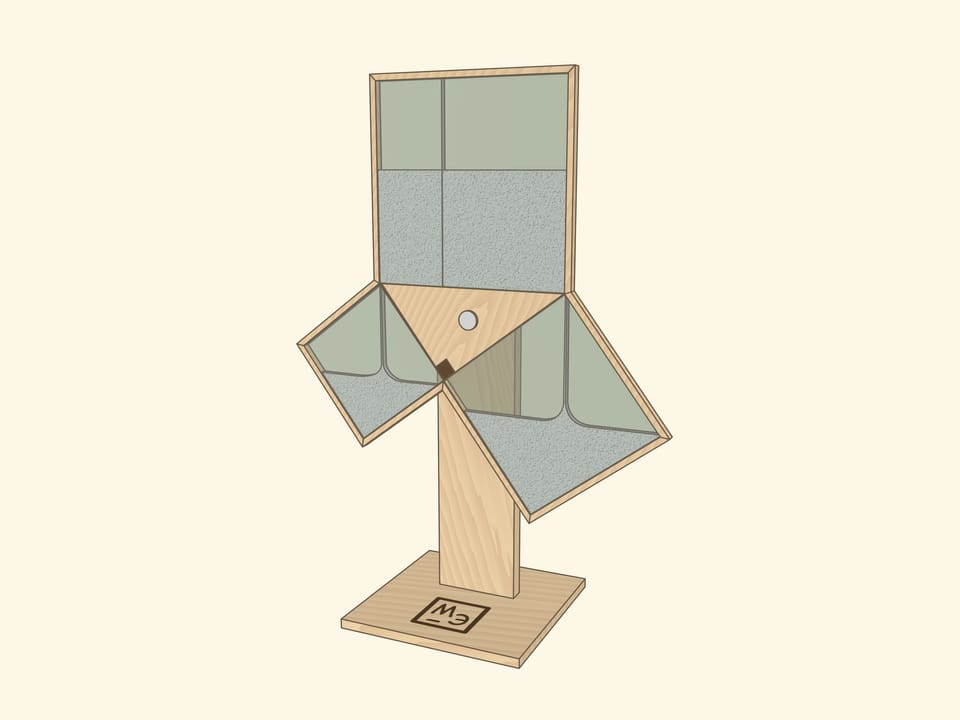
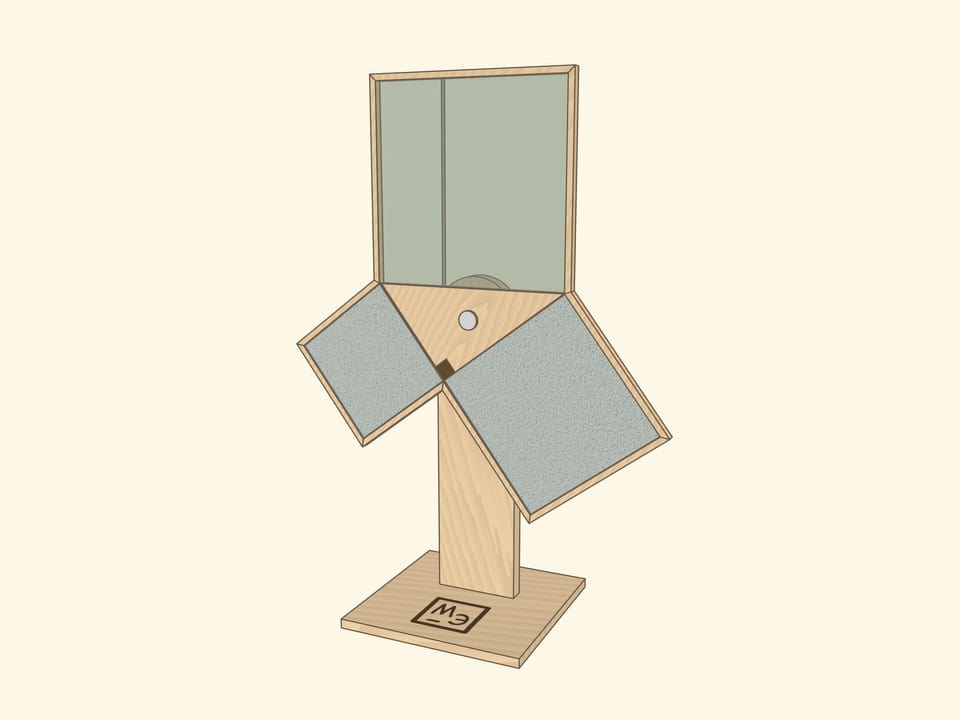
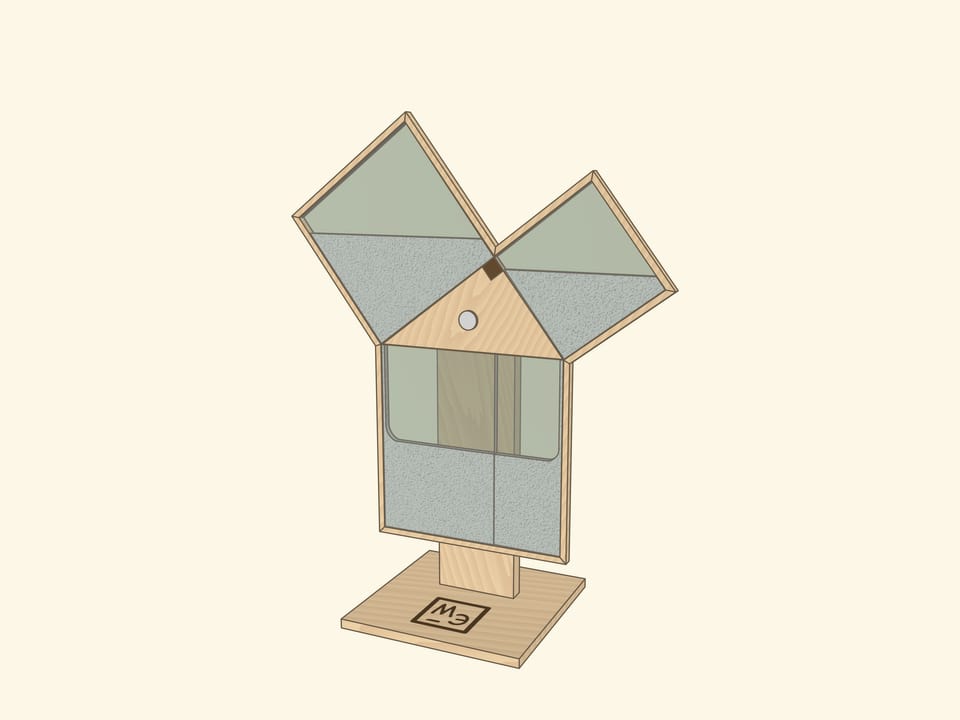
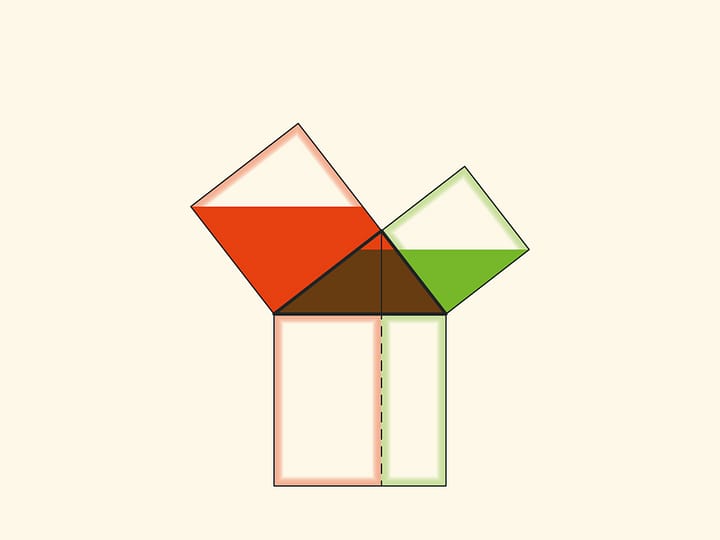
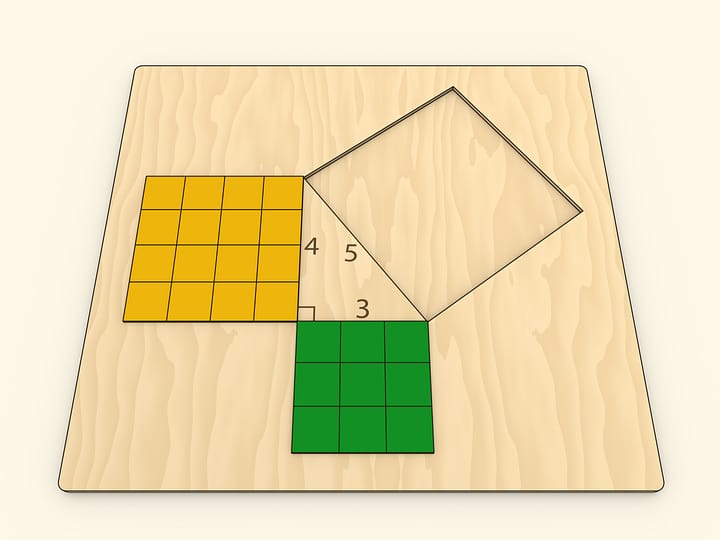
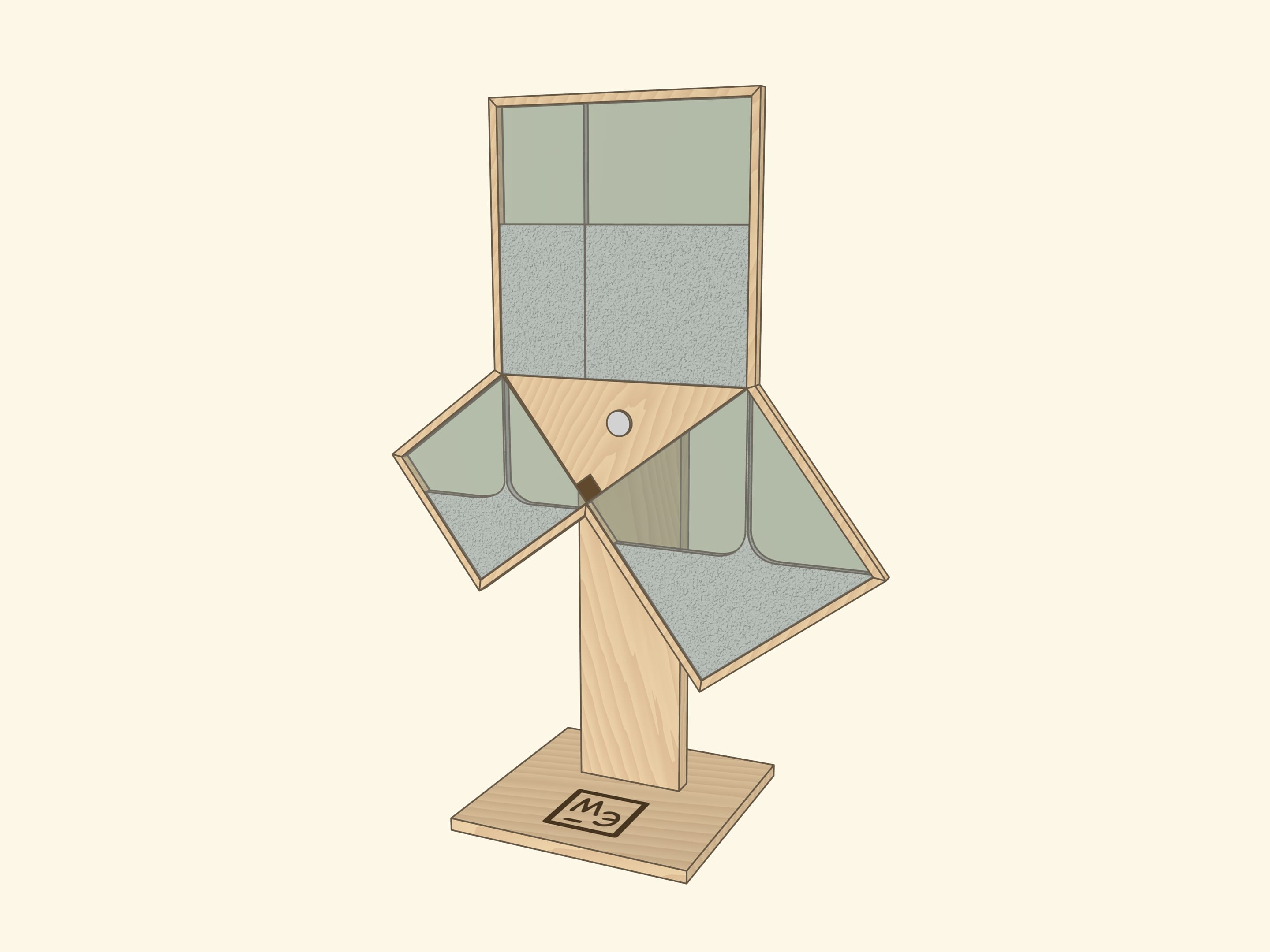
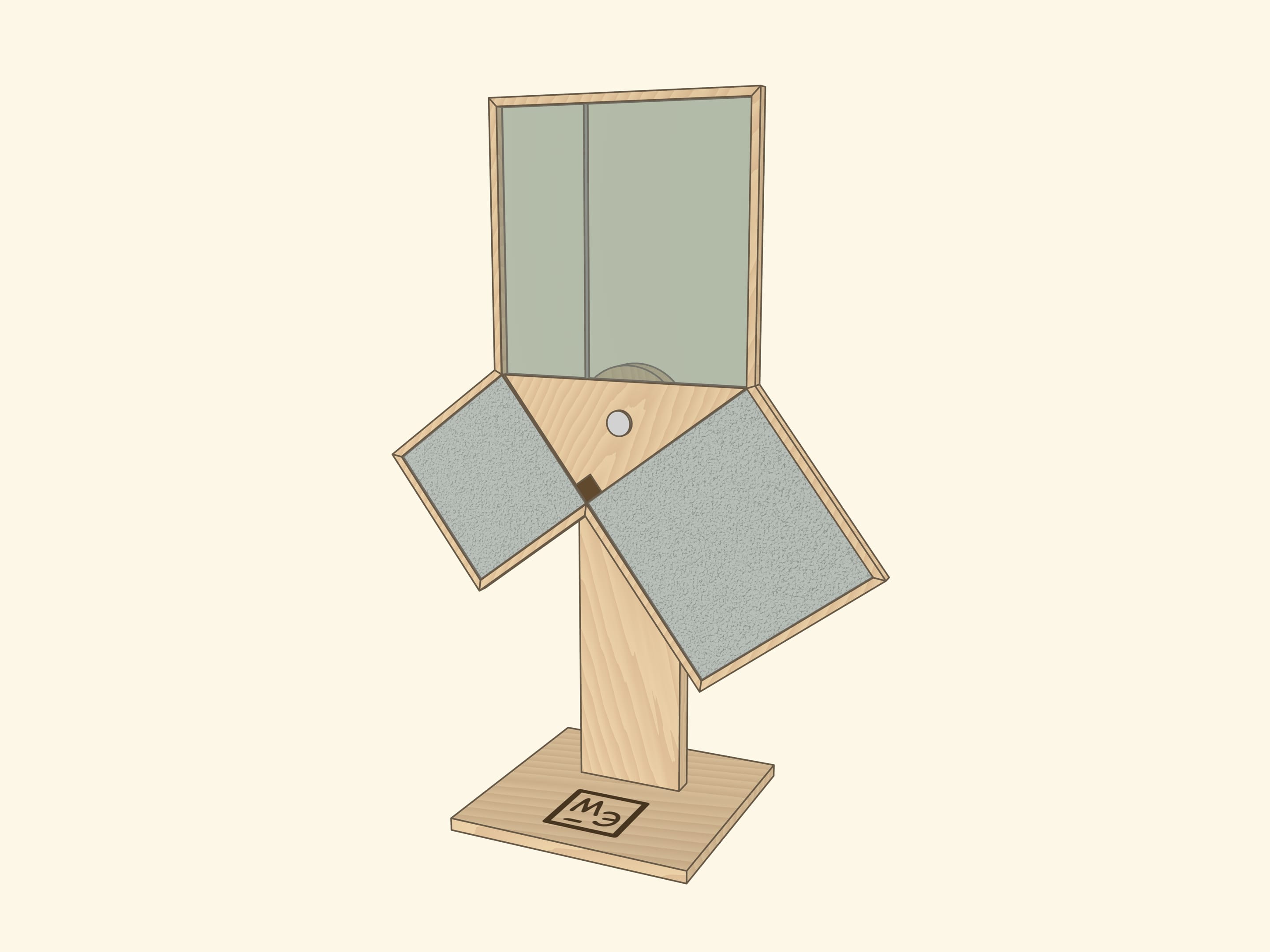
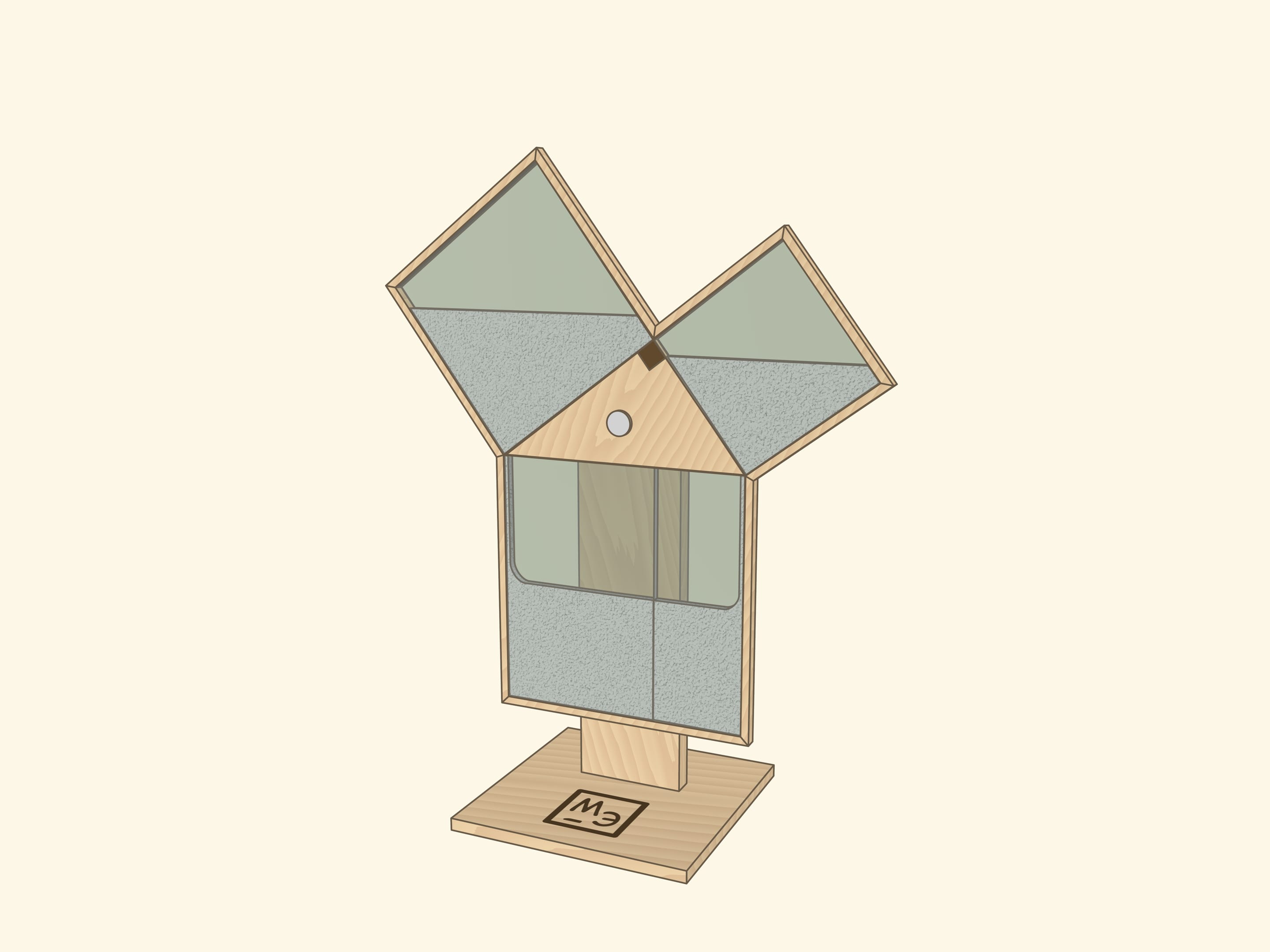
Наверное, во всех странах школьники учат теорему Пифагора, и во многих музеях науки можно встретить иллюстрирующий её экспонат, чаще не с песком, а с водой.
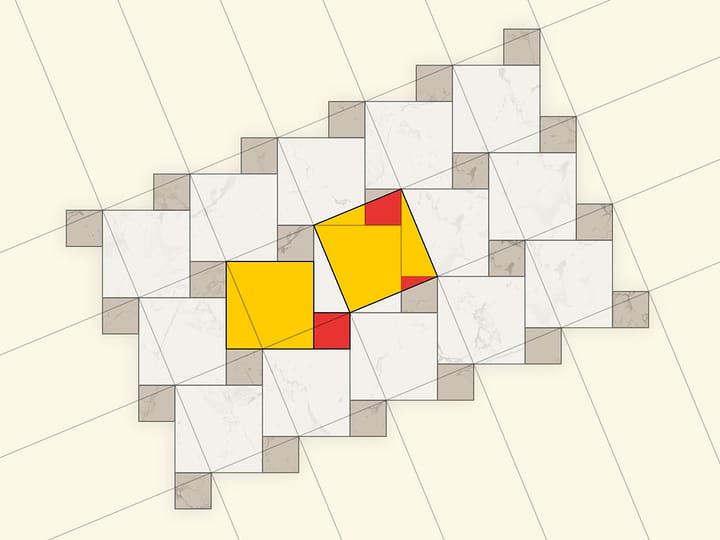
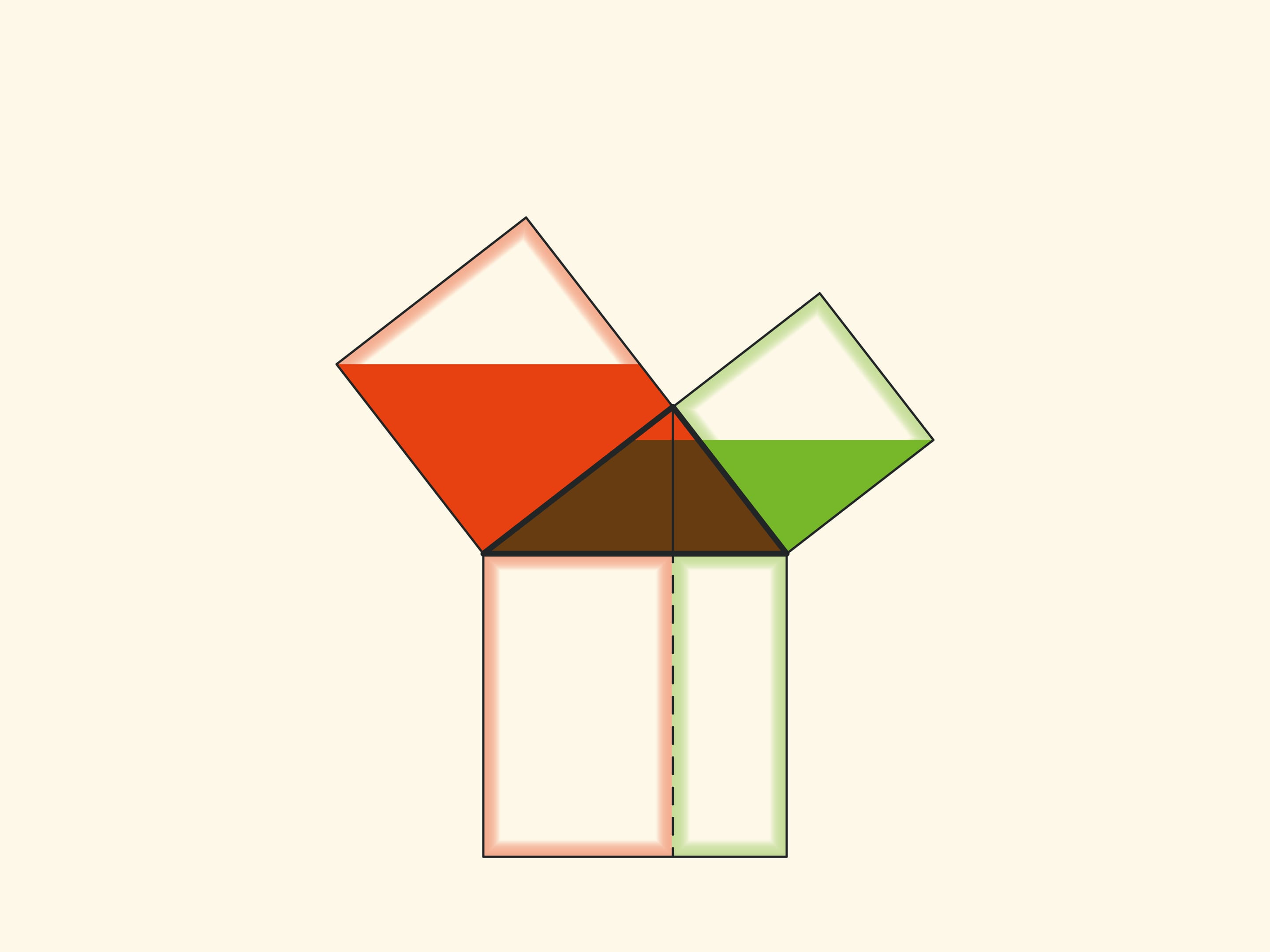
И в том, и в другом случаях важно следить, чтобы квадраты были заполнены полностью — речь же идёт про равенство площадей! Технически и визуально этому могут помочь закрытые от взора наблюдателя полосы между квадратами с «запасами» песка или воды.
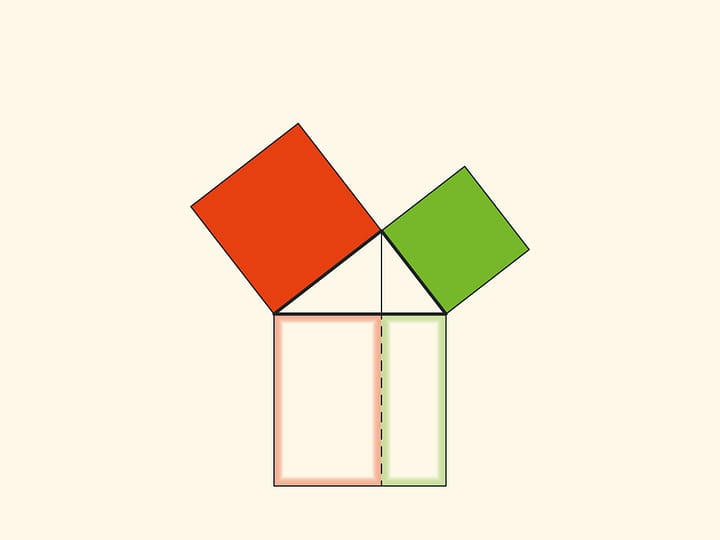
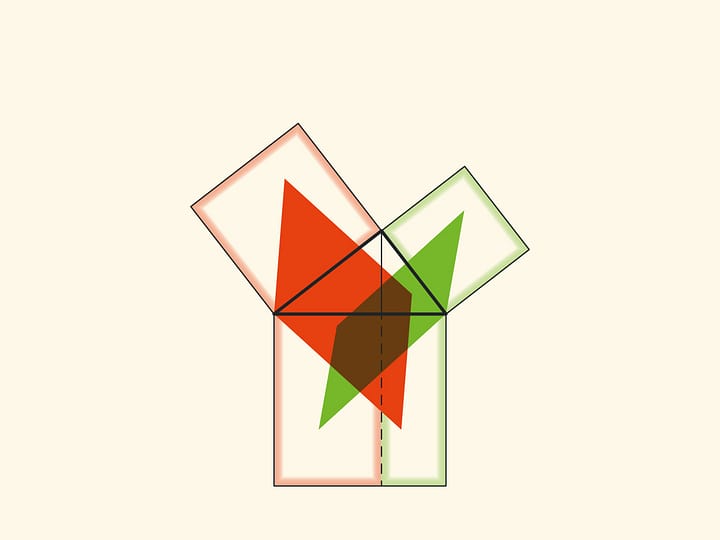
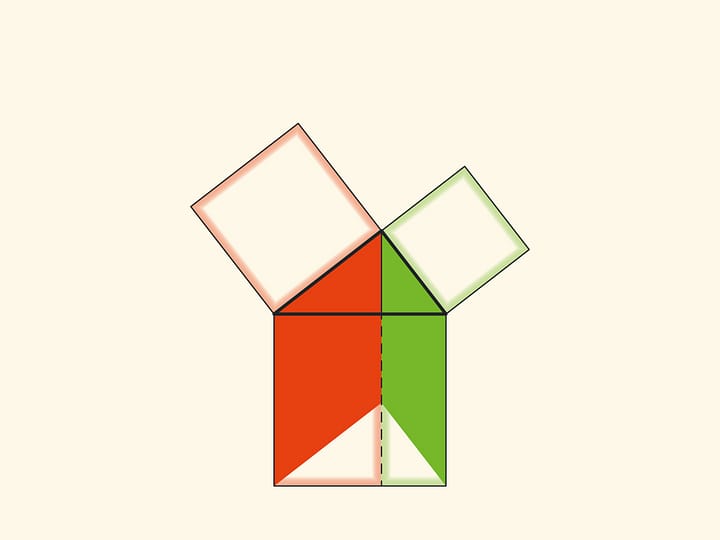
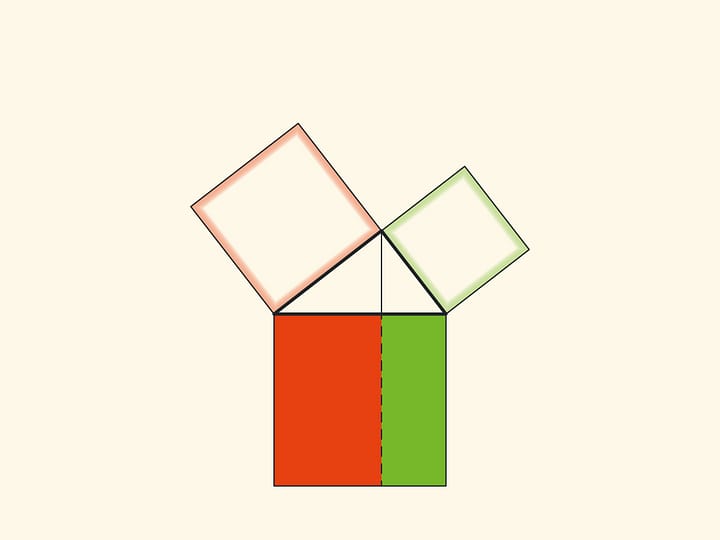
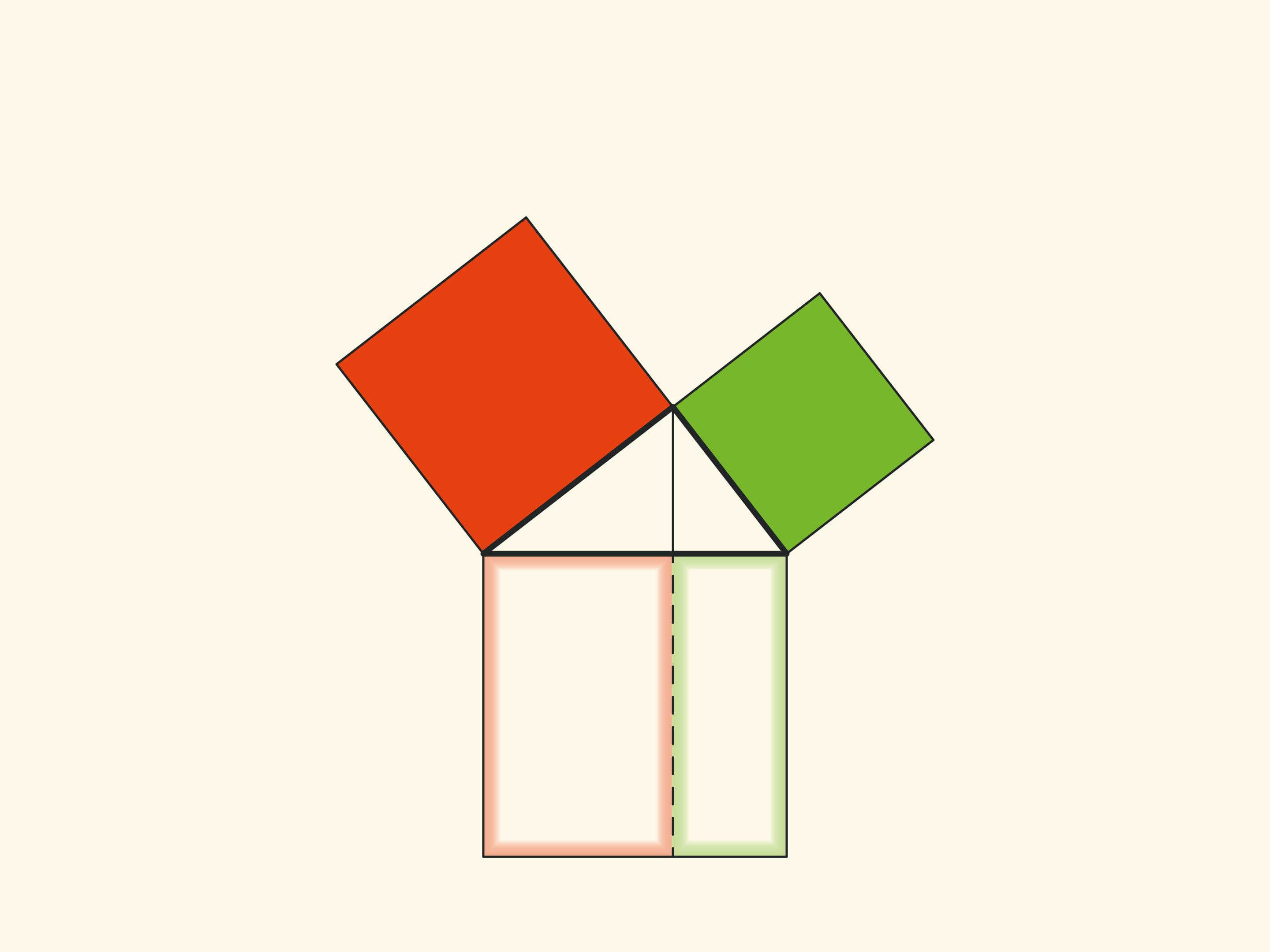
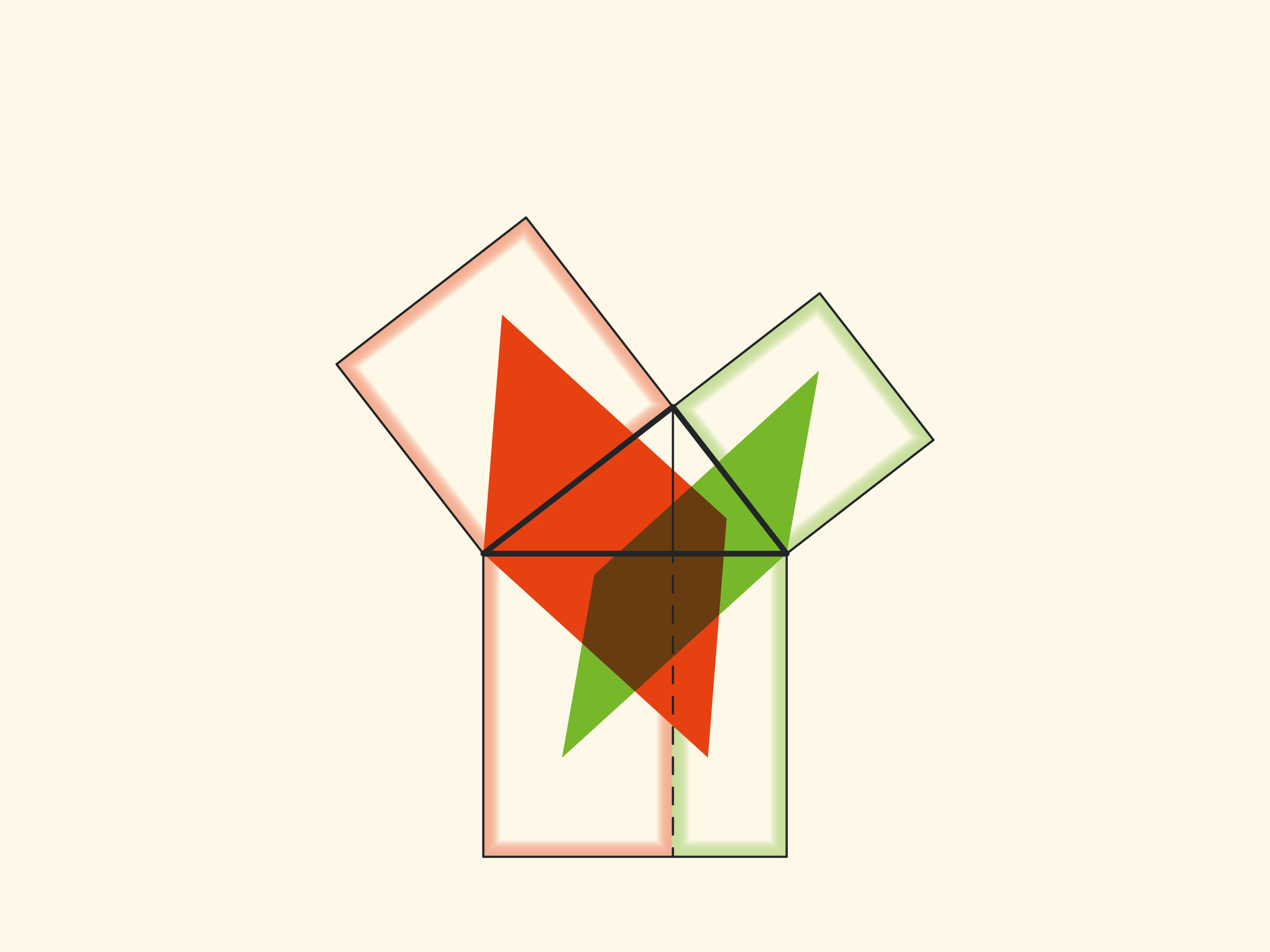
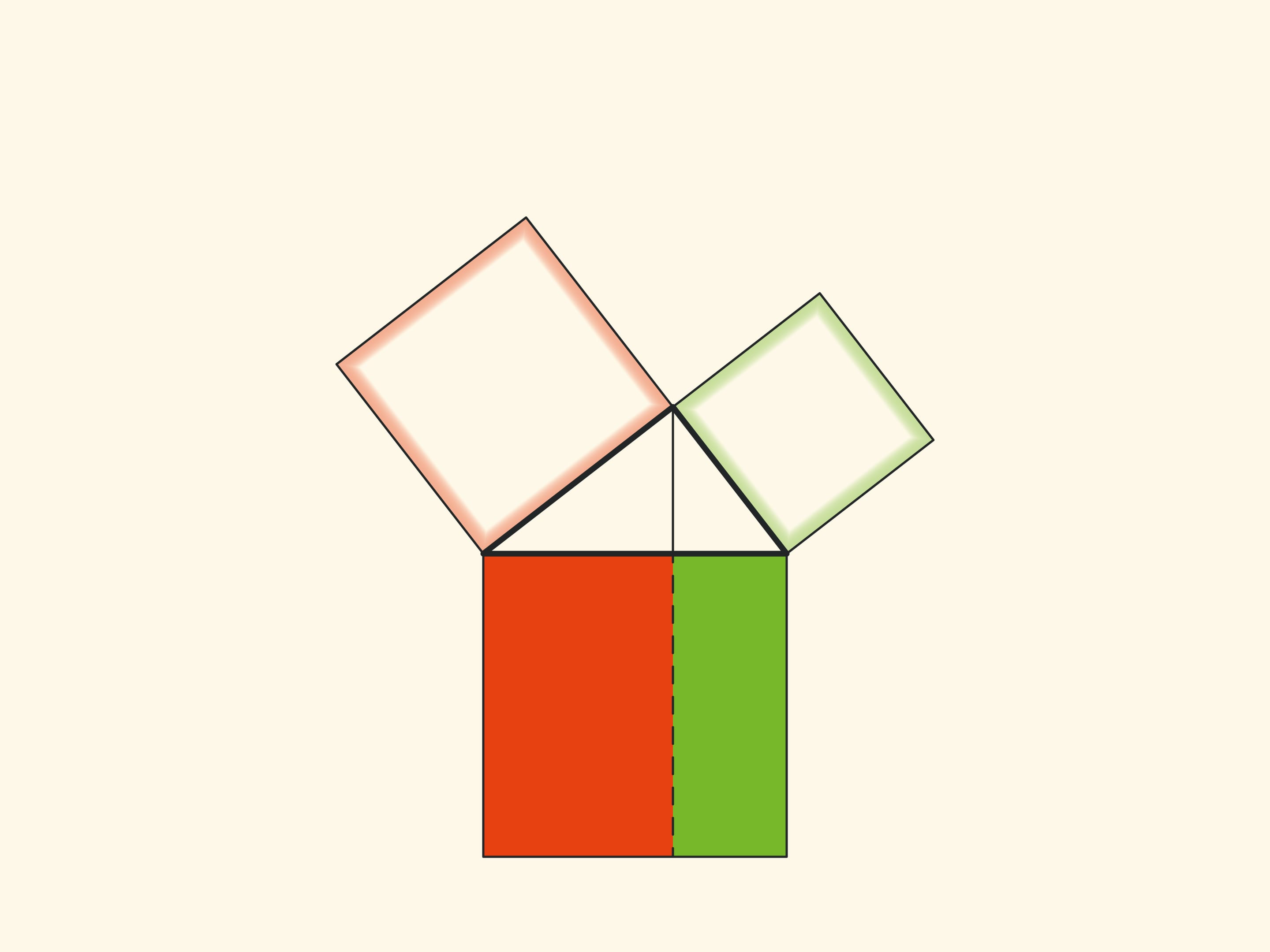
Обратим внимание ещё на одну важную деталь. Квадрат, построенный на гипотенузе, разделён на две части продолжением высоты прямоугольного треугольника, опущенной из вершины прямого угла. Оказывается, меньший из образовавшихся прямоугольников по площади равен квадрату, построенному на меньшем катете, а больший — квадрату, построенному на большем катете.
Технически это позволяет работать с меньшими объёмами и, соответственно, с меньшими погрешностями. А главное, это наблюдение позволяет построить уже не иллюстрации, а настоящие доказательства теоремы Пифагора типа «Смотри!». Причём по сути аналогичные приведённому в «Началах». Эти красивые и элементарные доказательства можно посмотреть на странице Теорема Пифагора: доказательство Евклида.
Другие модели раздела «Теорема Пифагора»
