Сумма (внутренних) углов треугольника равна $180^\circ$. Выучиваем мы это в школе и на всю жизнь. Для треугольника на плоскости продемонстрировать это несложно.
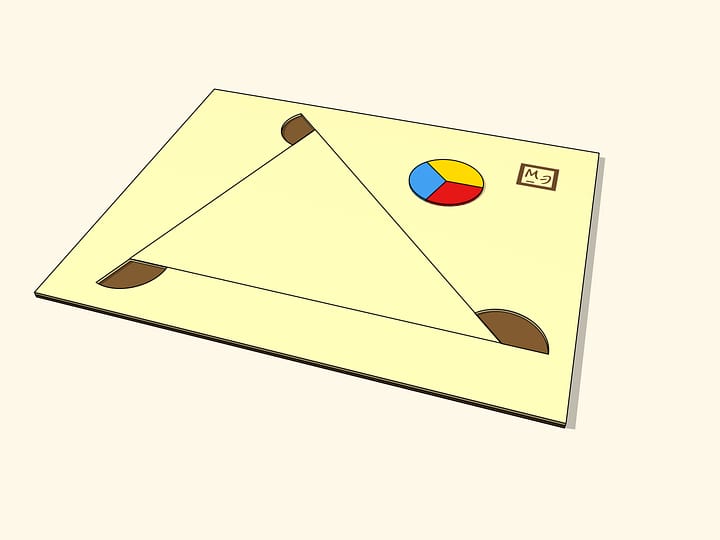
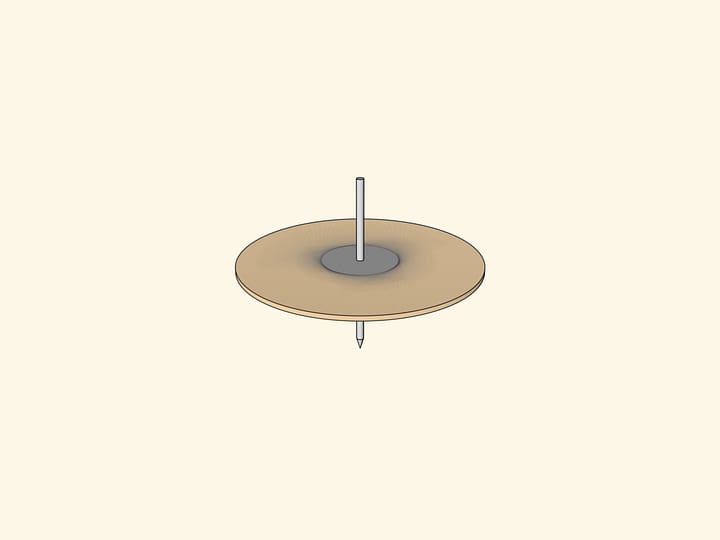
Первая идея заключается в том, чтобы сделать треугольник, например деревянный, с примагничивающимися углами.
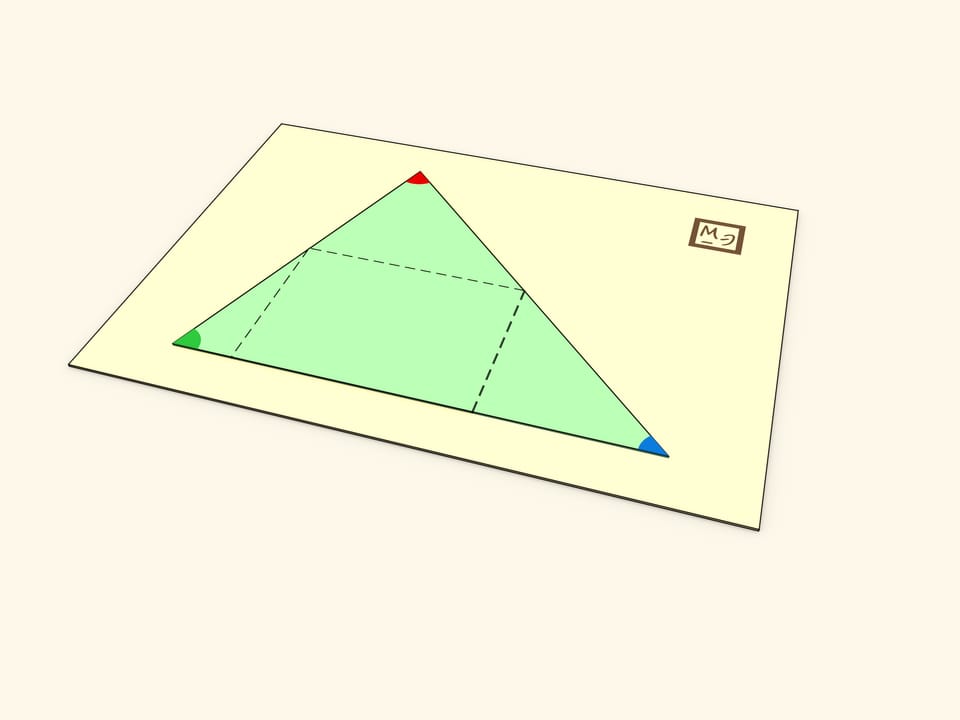
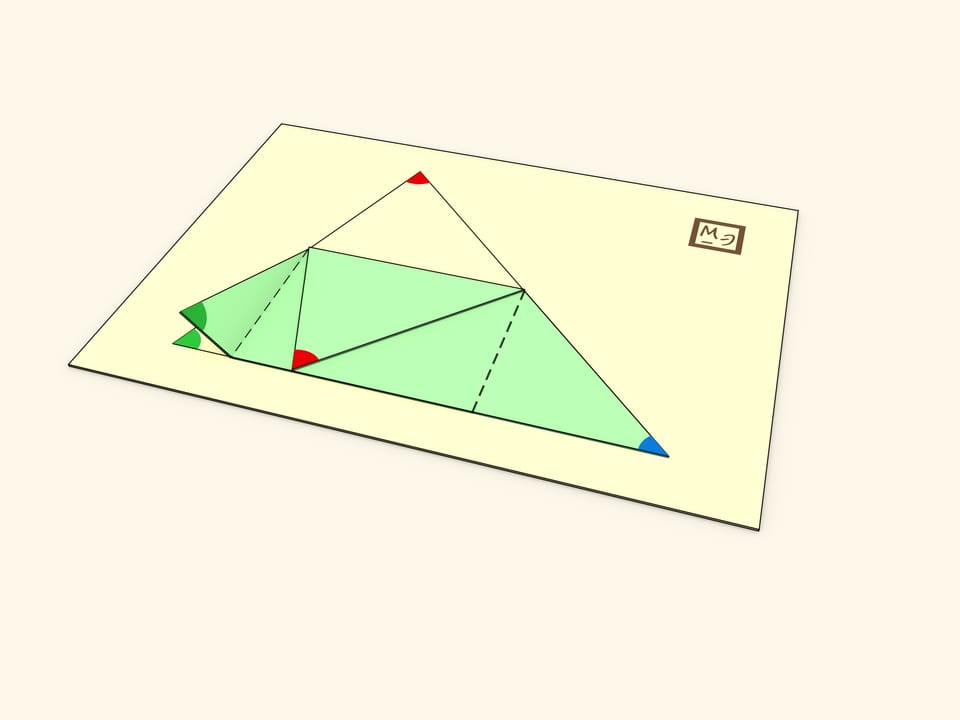
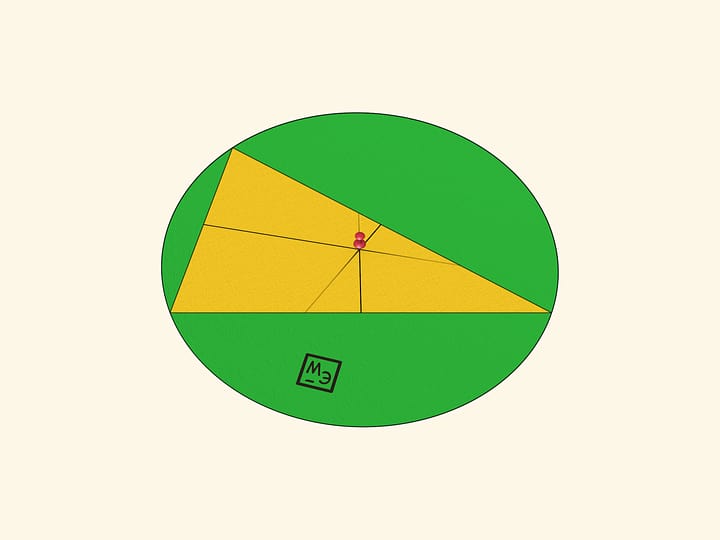
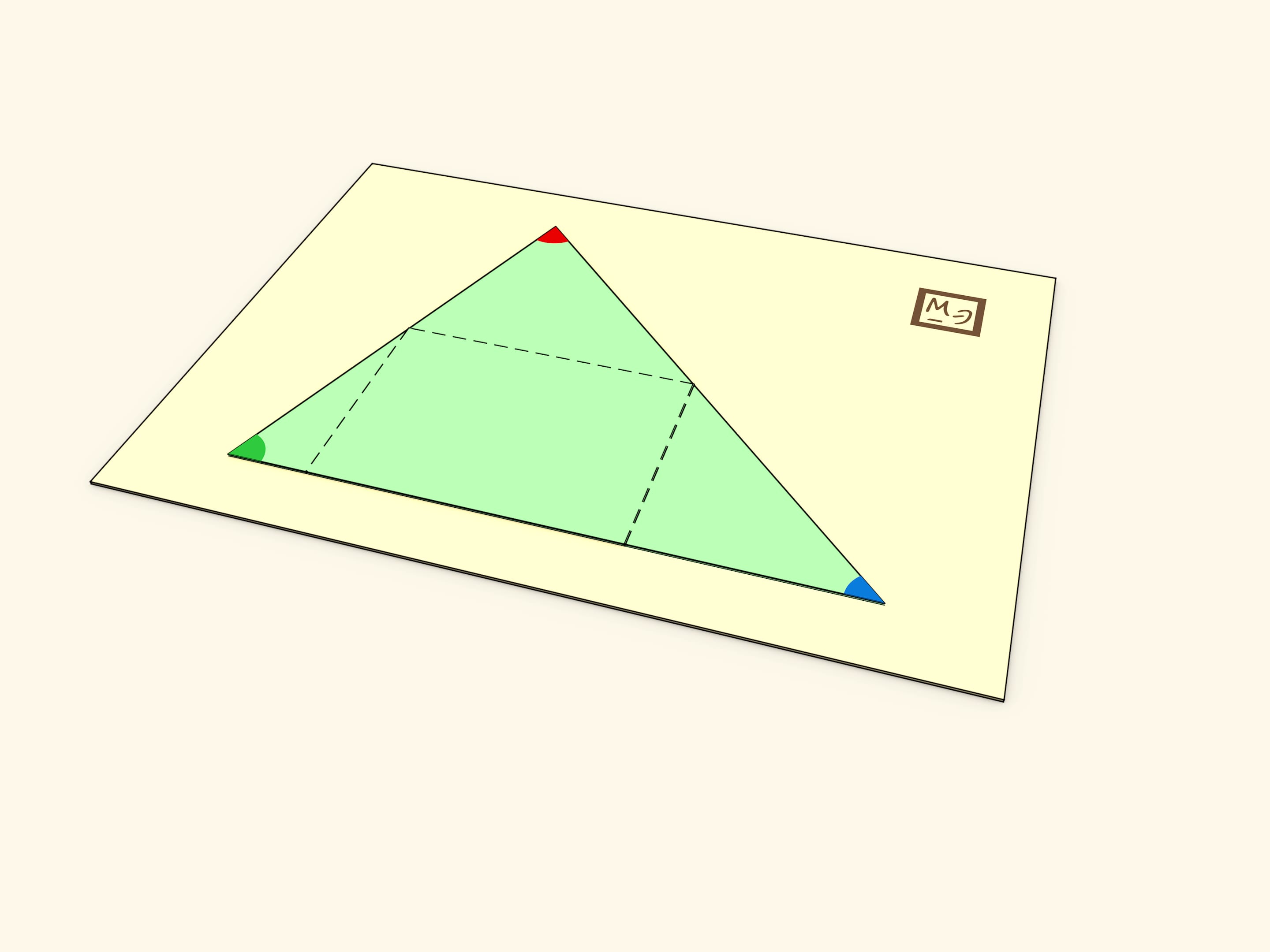
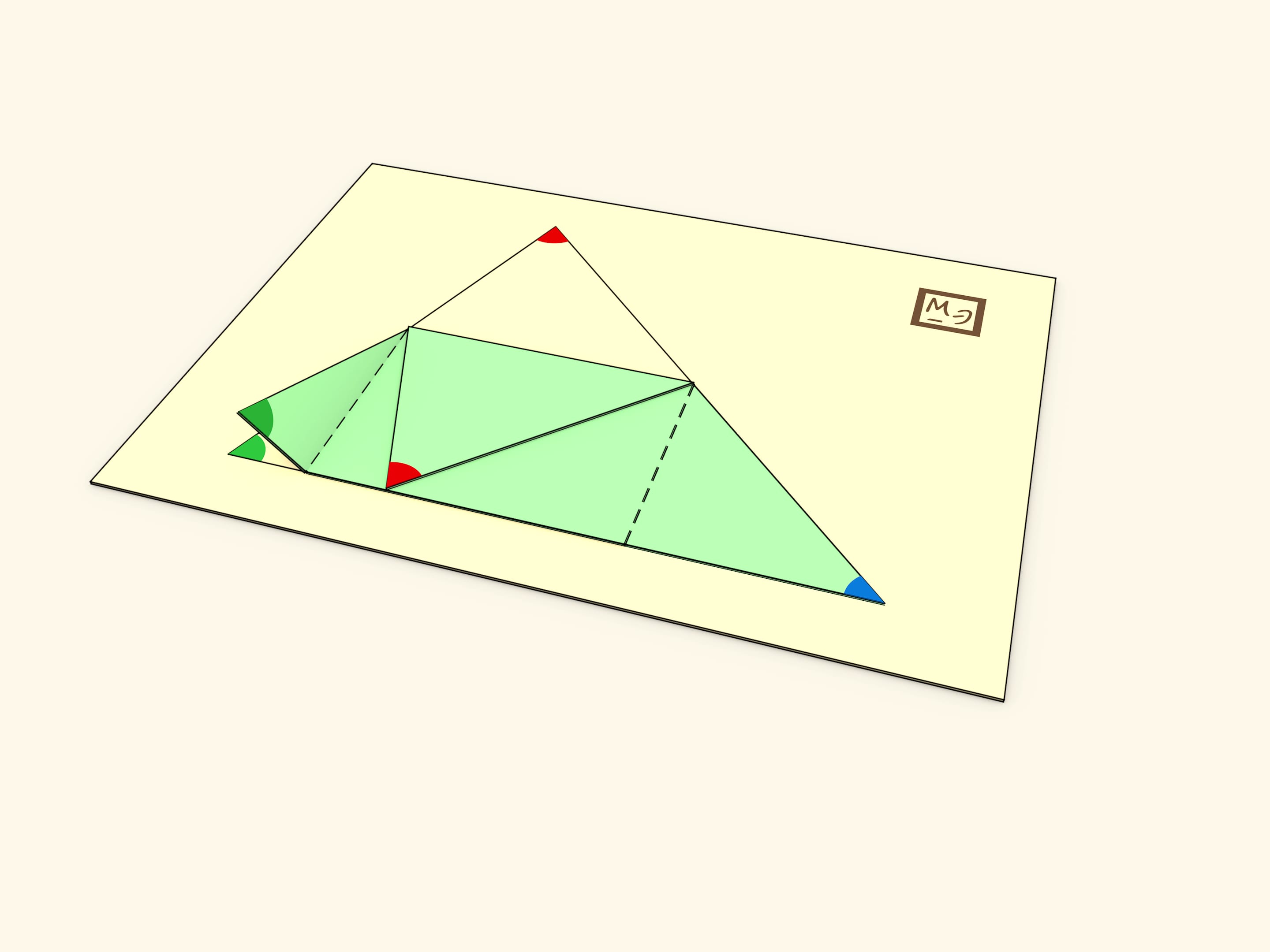
Вторая идея состоит в изготовлении складывающегося треугольника. В треугольнике, сделанном из картона или пластика, формируются три сгиба: один вдоль средней линии, два других вдоль перпендикуляров, опущенных из крайних точек средней линии на сторону треугольника. Конструкцию удобно наклеить на основание.
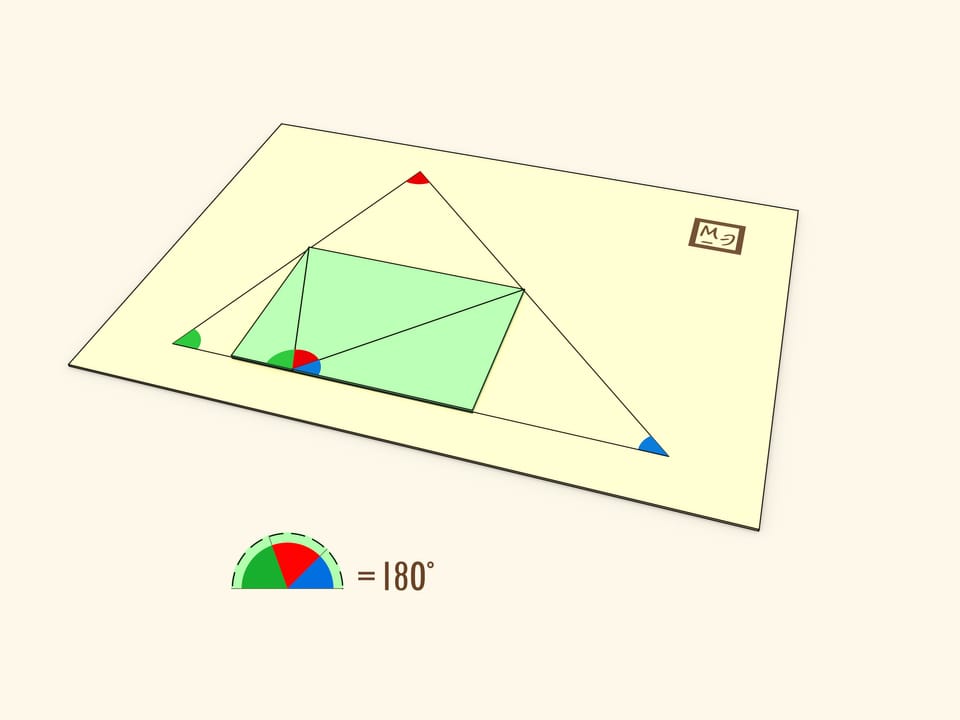
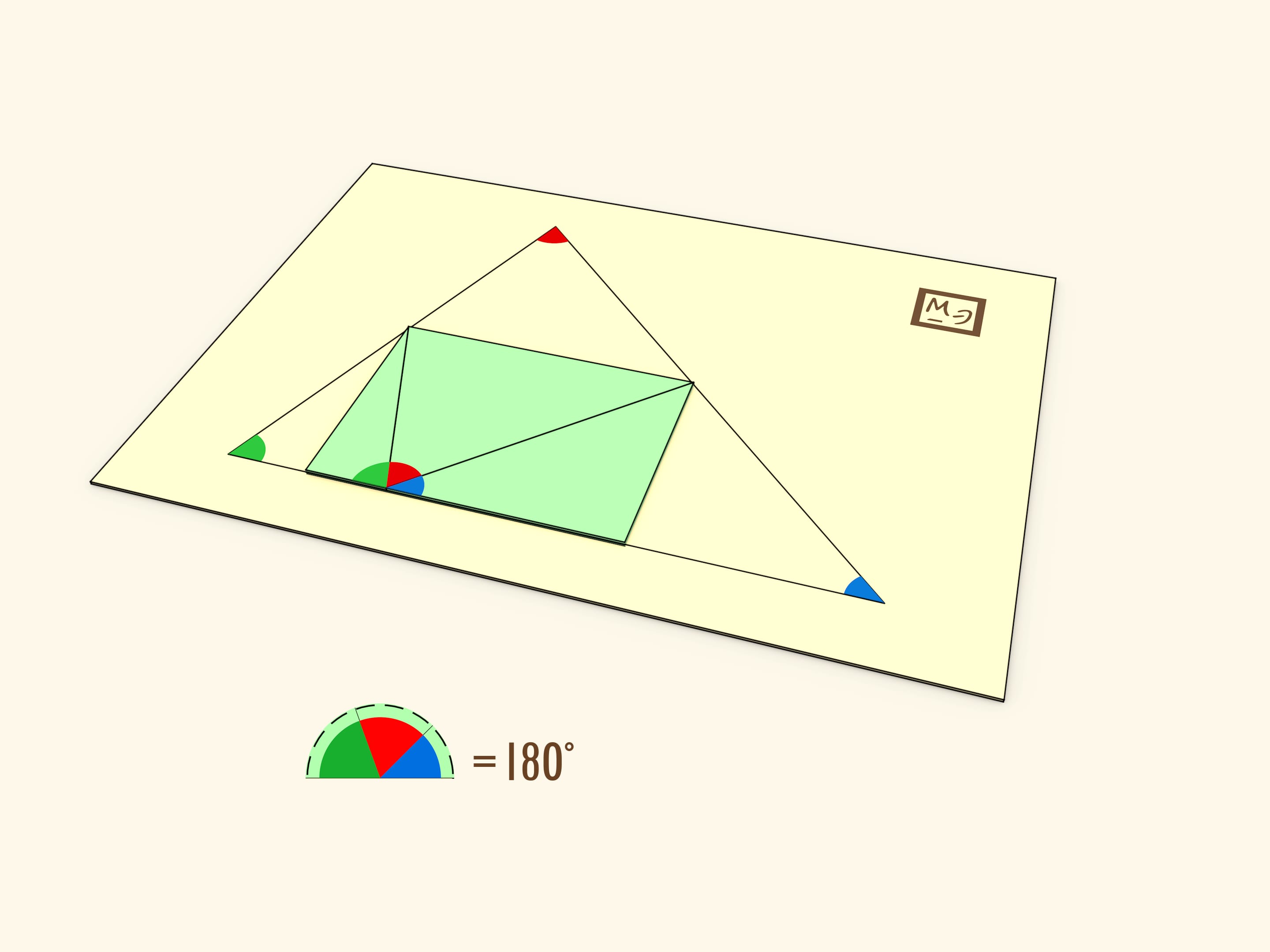
Если «сложить» треугольник, то все три вершины попадут в одну точку и внутренние углы треугольника сформируют развёрнутый угол.
На цилиндре и на конусе — точно так же — сумма углов треугольника равна $180^\circ$. Дело в том, что и цилиндр, и конус можно сделать из плоского листа бумаги. Нарисованный треугольник, при развороте листа на плоскость перейдёт в обычный треугольник без искажений.
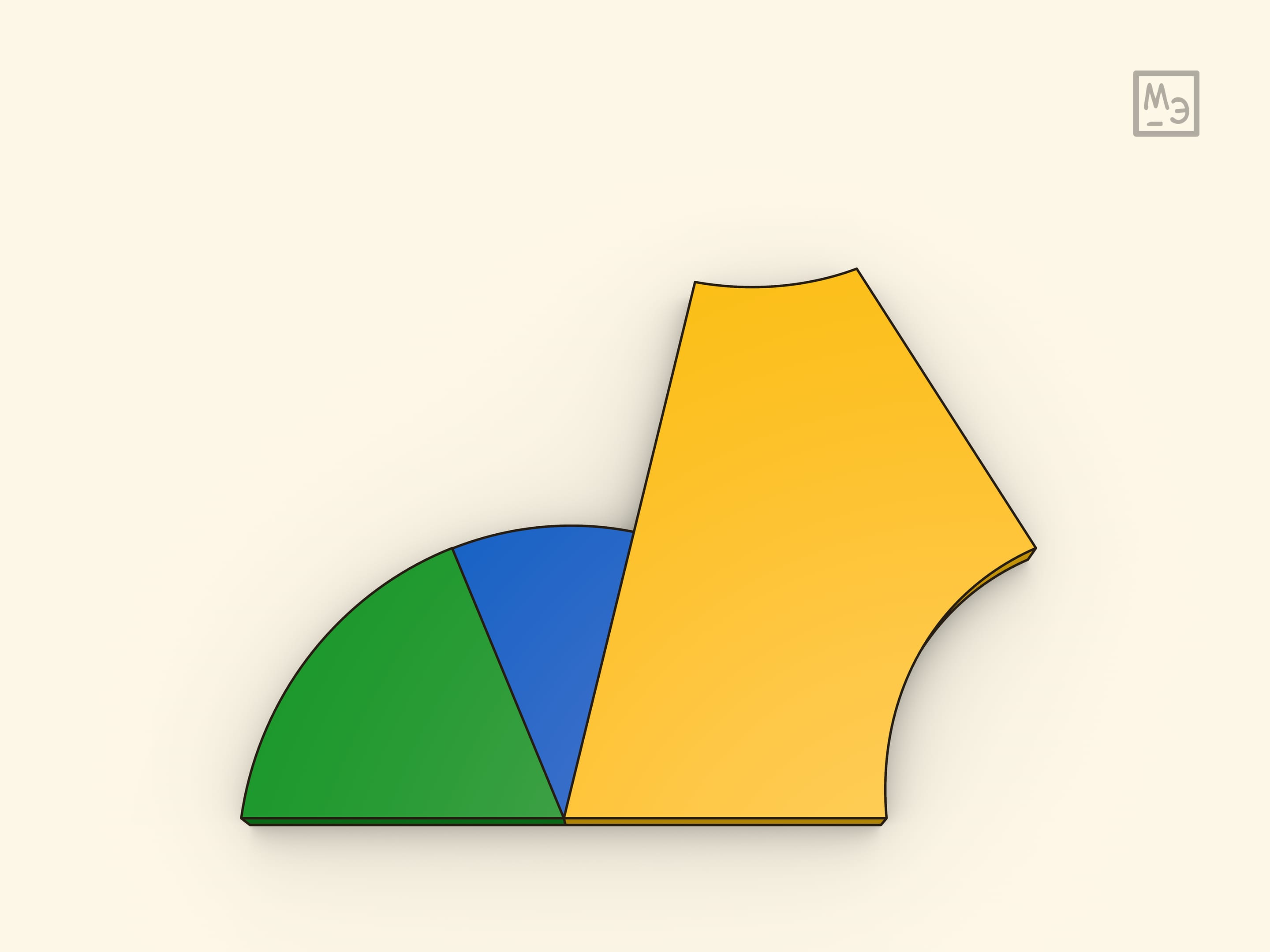
А вот в неевклидовых геометриях сумма углов треугольника отличается от 180 градусов. Например, на сфере легко придумать треугольник, у которого все углы — прямые.
Смотри также
Искривлённые миры // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 222—227.